• View
• Edit
• History
• Print

I am keeping this diary so that we all can see what I'm studying in mathematics. Also, you can look at my pages Recent Changes in Research and Recent Changes in Exposition.

In particular, I listen to videos while I exercise or do mundane chores.

Diary

2023.03.03 https://www.math4wisdom.com/wiki/Research/InterpretingYonedaLemma

2023.01.25 I am collecting material for a video where I overview the Binomial theorem as a portal for God in math. I will also make some videos where I tutor Bill Pahl about this.

2023.01.24 Thank you to Tom Koornwinder! for kindly writing out the details so that I could understand a key step in the derivation of the classification of Sheffer polynomials given in his and Paul Butzer's paper Josef Meixner: His life and his orthogonal polynomials.

2022.12.19 I am completing a video of John Harland teaching me linear regression.

2022.12.16 I am making slides for my Wondrous Wisdom Update about my ongoing research into wisdom.

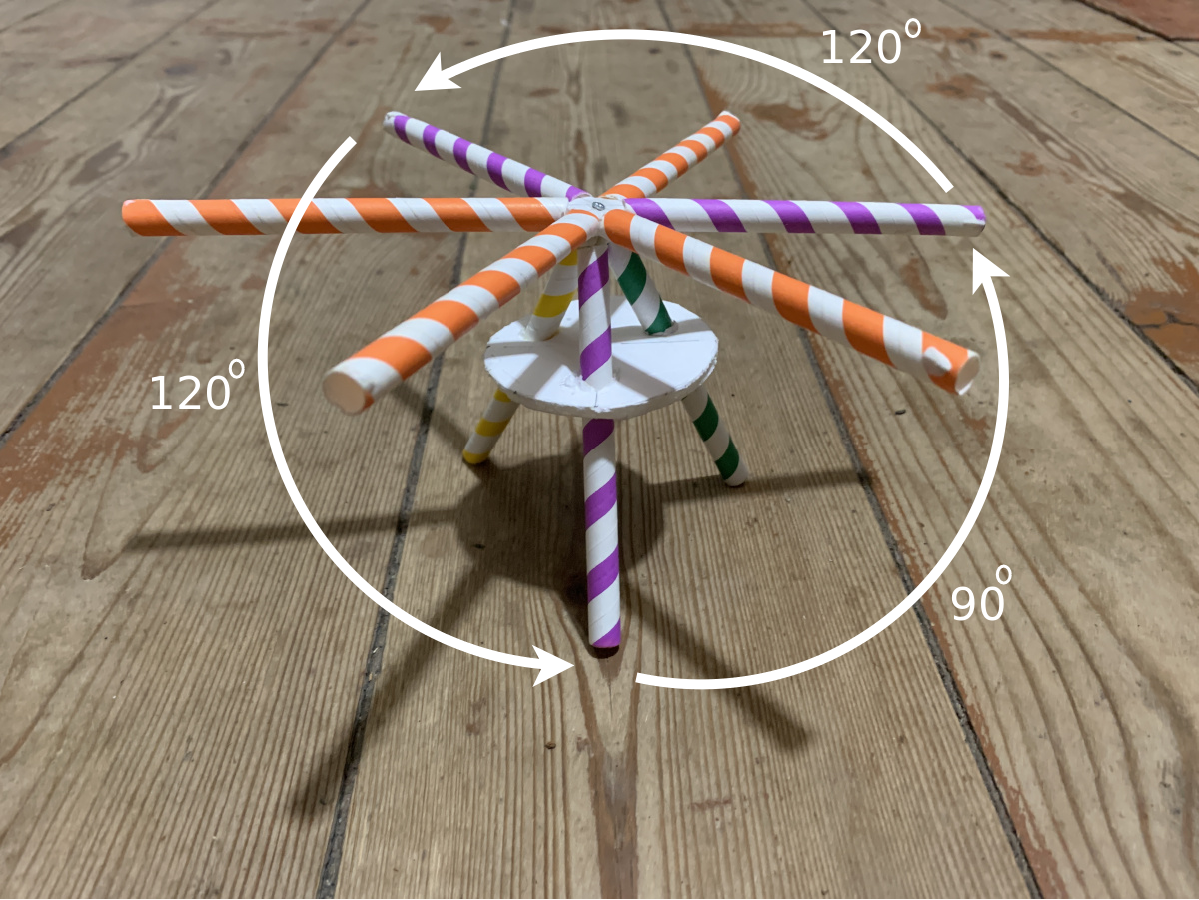
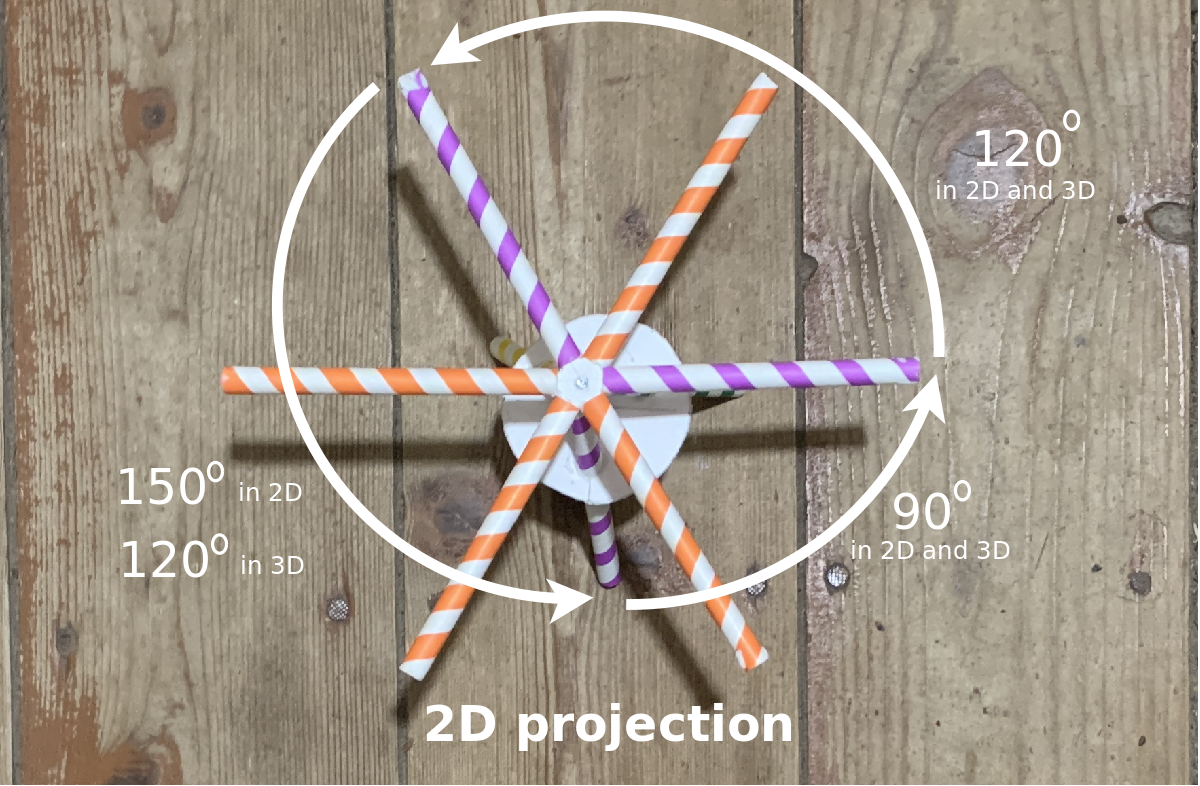
2022.12.14 I am using straws, foam board, ribbon and modeling clay to build three-dimensional models of the root system {$A_3$} of {$SU(3)$}. I want to understand geometrically how two rotations by {$120^\circ$} yield a rotation by {$60^\circ$}. This will help me imagine the chain which is at the heart of almost all Dynkin diagrams. I am making a short video about this: Root system {$A_3$} chains together the geometry of n-dimensional space.

2022.06.27 John Harland has impressed upon me the signficance of Stone's theorem on one-parameter unitary groups. I am trying to relate that to the generating function for Sheffer polynomials. I would like to claim that the only physical solutions to the Schroedinger equation are orthogonal Sheffer polynomials.

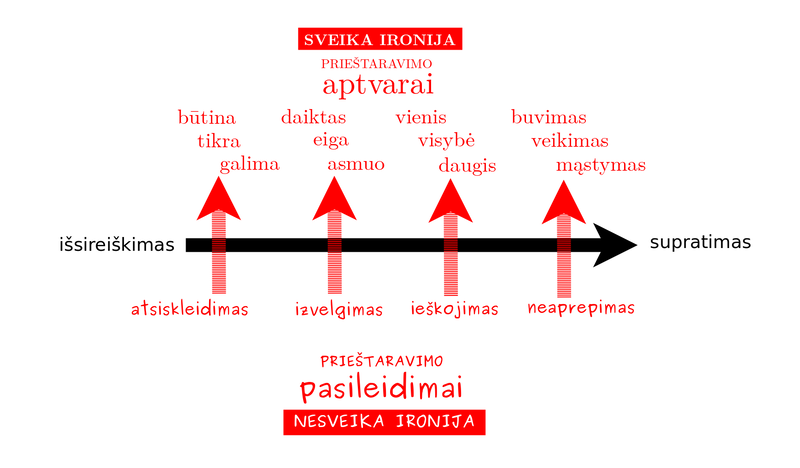
2022.05.27 I gave a talk on "Irony in the Memoirs of Those Who Knew the Perpetrators of the Holocaust" at the Lithuanian Cultural Studies Institute's conference on "Aesthetics, Philosophy of Art and Creative Activity in the Times of Social Transformation". Here is the original in Lithuanian and a machine translation into English.

2022.04.15 I responded to Russia's invasion of Ukraine with a talk, "A Peacemaker's Way: Wake Up, Love Your Enemy, Befriend Evil", which I gave in Vilnius at the Lithuanian Cultural Studies Institute's conference on "Civilizational Imagination and Contemporary Shifts in Geopolitics".

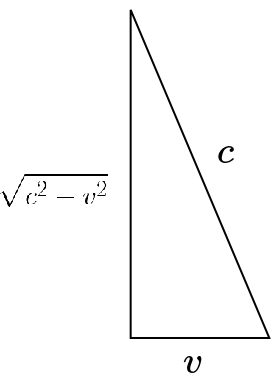
2022.03.28 I have been trying to understand how special relativity enters into quantum field theory. Studying with John Harland, I developed my own understanding of special relativity. I focus on the problem, which follows from the Pythagorean theorem, that the speed of light is different for different observers. And I show that the mathematics becomes elegant if we set {$c^2-v^2=1$} rather than {$c=1$}. My approach suggests to me that physics should be based on pairs of frames rather than single frames.

2022.02.22 Here in Lithuania I am deeply concerned by Russian autocrat Vladimir Putin's bullying of Ukraine. I learned a little bit about Ukrainian patriot Mikhail Kravchuk, whose Kravchuk polynomials I have been studying these last few days. In my understanding, his polynomials are a discrete version of the Meixner polynomials and, for my purposes, probably more important. The Kravchuk polynomials are orthogonal with respect to the (discrete) binomial distribution and I have investigated how they might relate the Hermite polynomials which are orthogonal with respect to the (continuous) normal distribution. The crucial difference is that the mean and the variance of the binomial distribution depend on {$N$} and get ever shifted to the right as {$N$} grows. The shift in the mean is given by {$N(\alpha - \beta) = Np$} and the distribution is given by {$w((\alpha-\beta)n)=(\frac{\alpha}{\beta})^n\binom{N}{n}$}, which only makes sense when {$\alpha\neq\beta$}. Should {$\alpha=\beta$}, then the mean does not move and so we take {$N\rightarrow\infty$} which gives the normal distribution. Thus, curiously, the continuous cases (Hermite, Laguerre) are a degenerate versions of the discrete case. I note that in the (quantum?) discrete case we have movement of the global space but in the (classical?) continuous cases the global space is at rest.

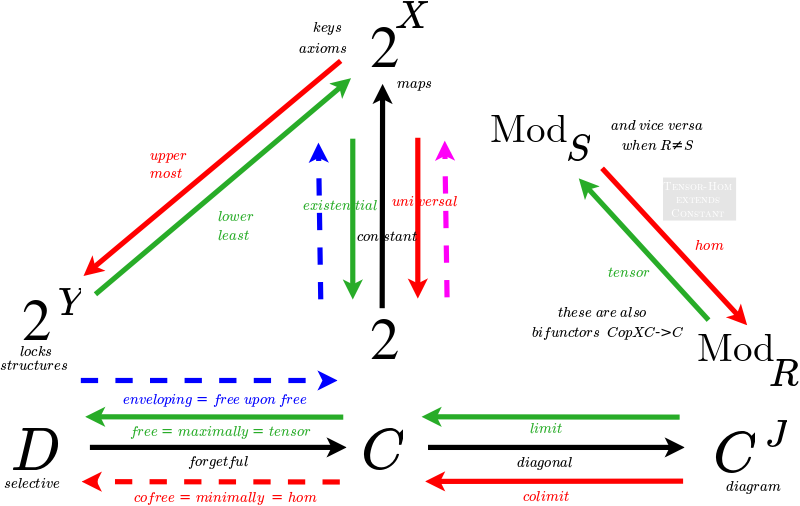
2022.02.02 I'm focusing on classifying adjunctions. I would like to better understand how they relate to how, in my philosophy, I define perspectives and especially, divisions of everything into perspectives. I think I'm making good progress, as with the diagram above. I think it is important to consider the two categories an adjunction is relating. What is the relationship between these two categories? The results seem to show the parallels between category theory (limits, colimits), algebra (defining structure maximally, minimally), logic (existential, universal quantifiers) and programming (currying, tensor, hom). Thus this may be a way of thinking about the Curry-Howard-Lambek correspondence. I still don't understand how it relates to my philosophy but perhaps it relates to the sevensome of dualities below.

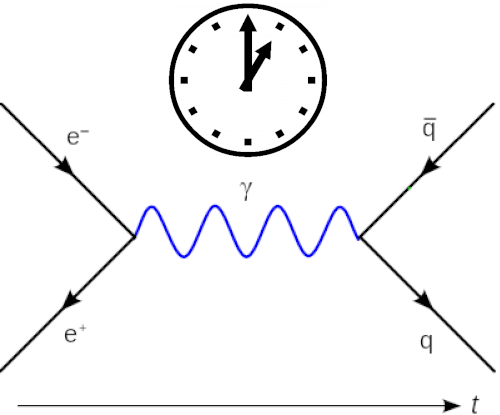
2022.01.29 In thinking about the combinatorics of the Sheffer polynomials, I realized that each particle can be interpreted as having a clock. The clock relates two coordinate systems by steps {$\alpha$} going from one to the other and steps {$\beta$} going back. Each step in space can be thought as a tick by the clock. The five kinds of Sheffer polynomials reflects the ways that {$\alpha$} and {$\beta$} can degenerate. Physically, we have five zones in a scattering problem.

Distant past	Unentangled	{$\alpha,\beta$}	Meixner polynomials
Entering interaction potential	Wave packet	{$\alpha, 0$}	Charlier polynomials
Within interaction potential	Bound state	{$\alpha,\alpha$}	Laguerre polynomials
Leaving interaction potential	Free space (perturbed)	{$0,0$}	Hermite polynomials
Distant future	Entangled	{$\alpha,\bar{\alpha}$}	Meixner-Pollaczek polynomials

Imagine particles as marbles, and imagine their interaction potential as an invisible bowling ball which they bounce off of. In the distant past, the potential is so weak that by Heisenberg's principle it is nonexistent. Likewise in the distant future. At some point the particle enters the potential, is within the potential, and leaves the potential. Currently, quantum field theory models events in terms of the results of measurements as the particles is leaving the potential. This is the most degenerate situation, where the clock has been reset, which I take to mean the wave function has collapsed. The combinatorics is given by the contractions in Wick's theorem, which is the combinatorics of the coeficients of the Hermite polynomials that describe the quantum harmonic oscillator as well as free space. A particle's clock is a combinatorial elaboration of this contraction which evidently describes not the interaction potential but the kinematics, what the particle experiences as it links two vertices of an edge in a Feynman diagram, which is to say, how it relates the two vertices as two coordinate systems. I suppose that in order to make calculations based not on free space but on some other of the five frameworks, one needs to consider the relevant combinatorics of the clocks in calculating how the particle creation and annihilation operators act not on the null state but, for example, on a bound state. I believe that if this can all be described by particles with clocks, then it would automatically generate the Minkowski space of special relativity, and so there might not be a need to postulate a Lagrangian density manifesting the continuum, which seems to me like overkill, unnecessary and thus unphysical.

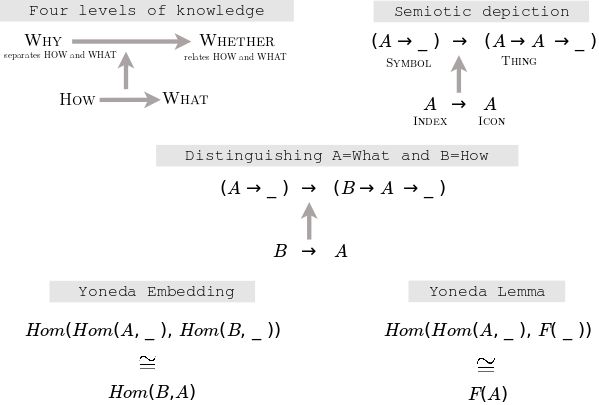
2022.01.12 Finally, after five years of effort, I have related the Yoneda Lemma to the four levels of knowledge: Whether, What, How, Why. It's actually the Yoneda Embedding which is relevant. A typical morphism goes from How to What. Why is the perspective that keeps How and What separate, and Whether is the perspective that relates them. Thus a mental shift from How to What is followed by a mental shift from Why to Whether. Why and Whether are contextual and given by the sum of relationships. Why is dynamic consciousness of those relationships whereas Whether preserves those relationships as knowledge. The levels of knowledge also express the scope of understanding, which is to say, the scope of separation: Why separates everything, How - anything, What - something, Whether - nothing, for with Whether it is no longer separated but is related. I will be explaining more of this in the introductory video in the series where I will present my research program.

2022.01.05 In studying Bott periodicity, I realized that for my purposes I should focus on the classification of Clifford algebras. I see that it is straightforward to construct the regular representation of a Clifford algebra by considering how the basis elements act on each other by multiplication. For example, I can define matrices for {$1$}, {$e_1$}, {$e_2$}, {$e_1e_2$} by describing what these basis elements yield when I multiply them on the left of {$1$}, {$e_1$}, {$e_2$}, {$e_1e_2$}. I can investigate what happens when I add a new element {$e_3$} for which {$e_3^2=q_3$}. I can study the combinatorics of the resulting regular representations and understand how they express {$\mathbb{C}$}, {$\mathbb{H}$}, {$\mathbb{H}\oplus\mathbb{H}$}, {$M_2(\mathbb{R})$} and other such structures. I can figure out how the regular representations break down into irreducible representations. My efforts will help me better understand the various readings.

I am also trying to master the adjunction of the loopspace functor and the reduced suspension functor, which is relevant for understanding the K-theory of Bott periodicity. Tai-Danae mentions this adjunction in giving examples of adjunctions and describes it in her exposition of the one-line proof that the fundamental group of a circle is {$\mathbb{Z}$}.

2021.12.26 I have been studying some helpful expositions of Bott periodicity, which I believe expresses the eight-cycle of divisions of everything, a circular tour of mental states. I am growing familiar with the concepts in the Wikipedia article. I appreciate Cameron Krulewski's accounts of Bott periodicity and the classification of topological insulators and superconductors. Her latter article includes a proof of the classification of Clifford algebras, which I wish to focus on. There is also a Wikipedia article for that classification. Other expositions of Bott periodicity are by Aygul Galimova, Anthony Bosman, Carlos Salinas, and in the complex case, Allen Hatcher. There is an important proof by Mark Behrens and a list of proofs on MathOverflow. And there is a paper by Jost Eschenburg and Bernhard Hanke that relates Clifford modules to vector bundles over spheres.

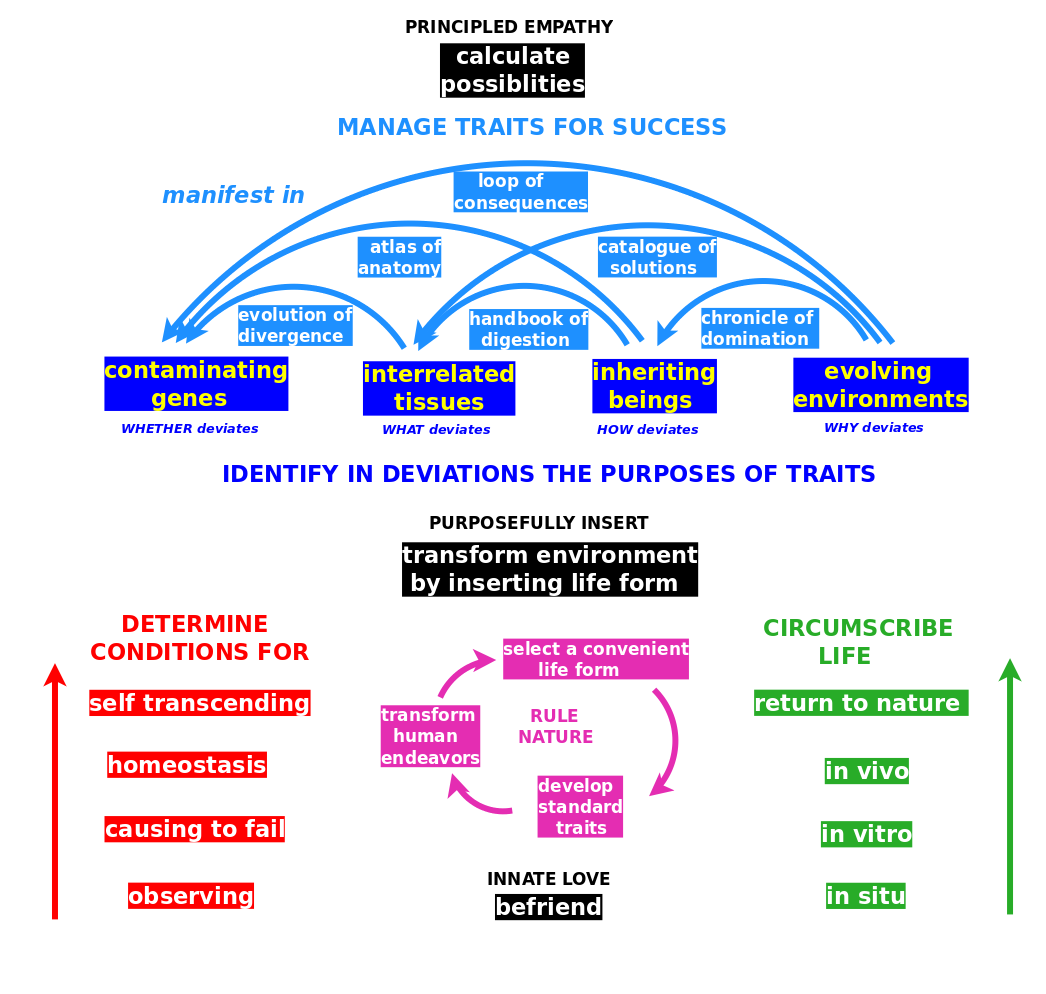
2021.11.05 I gave a talk on the 24 ways of figuring things out in biology. You can read a rather decent machine translation from Lithuanian into English: Adam Named the Animals: There Is Love of Life In the Epistemology of Biology. This investigation yields a definition of life as a system that manages its traits for success.

2021.09.02 I am making some progress understanding the adjunction that relates restriction and induction functors on categories of group representations. I want to master this and use it to illustrate the three definitions of adjunction.

Today, here in Lithuania, it's hard to focus on anything but Russia's attack on Ukraine. I am grateful to every Russian who dares to speak up against this war. You give me peace.

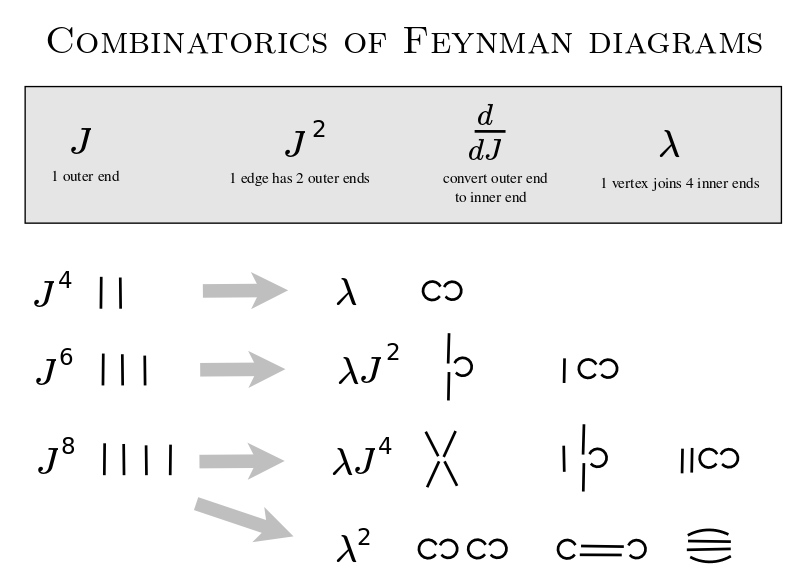
2021.08.01 After some perplexity, I now understand what it means to construct the possible Feynman diagrams given a power of {$J$} and a power of {$\lambda$}. I will be able to relate this to Wick contraction, which is also the basis for the combinatorics of the Hermite polynomials. So I am realizing it will be straightforward to think of the other Sheffer polynomials as extending quantum field theory to model what happens kinematically as a particle passes from one interaction to another. Kinematically, I intend to show that the particle can be taken to be in one of five natural coordinate systems: Hermite (empty space), Charlier (moving packet), Laguerre (bound state), Meixner-Pollaczek (scattering), Meixner (creation and annihilation).

2021.08.01 In physics, I am reading parts of Quantum Field Theory in a Nutshell by Anthony Zee and Introduction to Quantum Mechanics by David J. Griffiths. Then I will return to my investigation of Sheffer polynomials. I am trying to make sense of quantum physics, and specifically, the Schroedinger equation, by using combinatorics, algebra and analysis to investigate the fivefold classification of Sheffer orthogonal polynomials. I am interpreting this classification as a cognitive framework for decision making, for relating a subsystem and a system, based on two kinds of causality, backwards from effect to cause - every effect has had its cause, and forwards from cause to effect - not every cause has had its effects. I zoom every other Monday with John Harland.

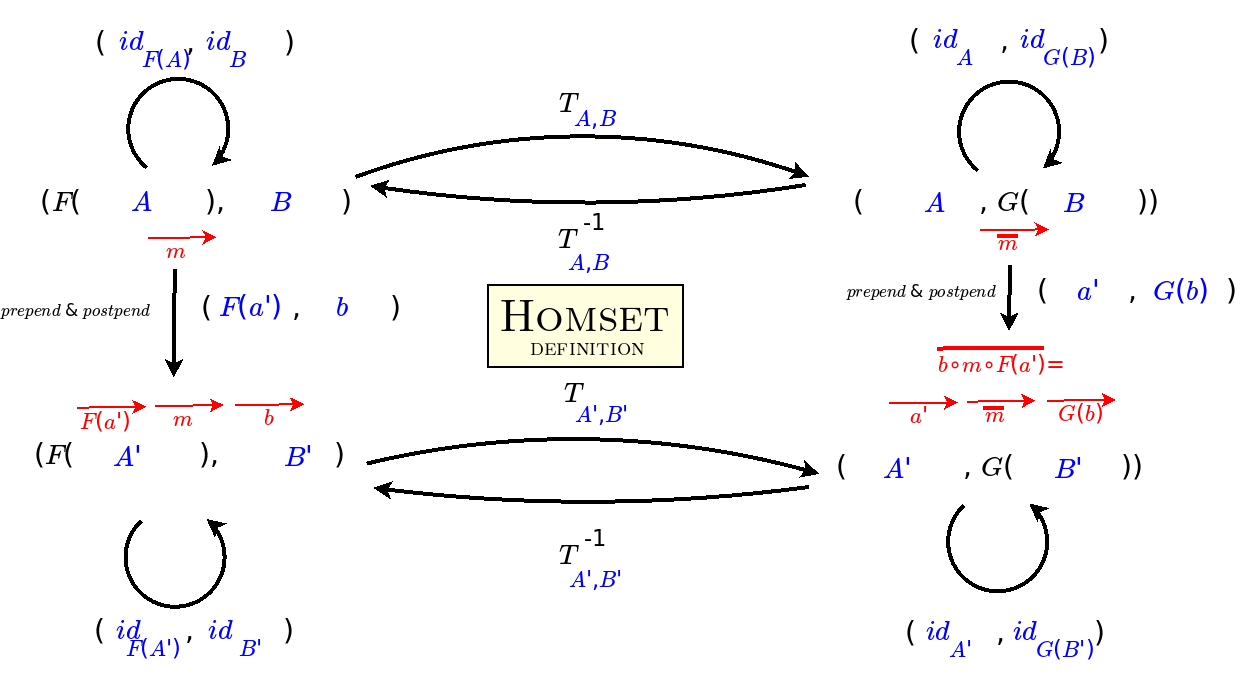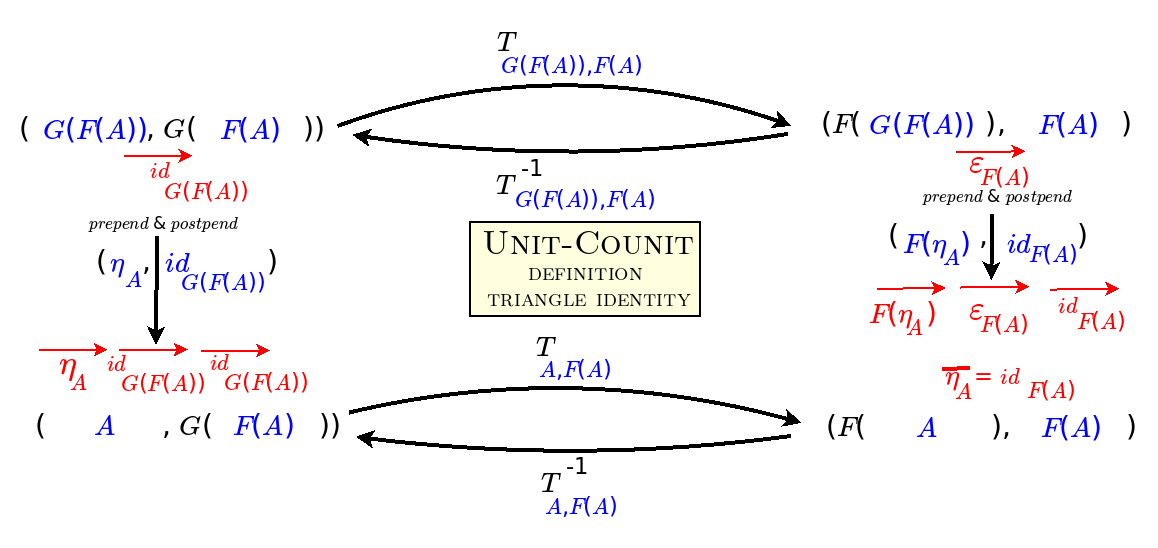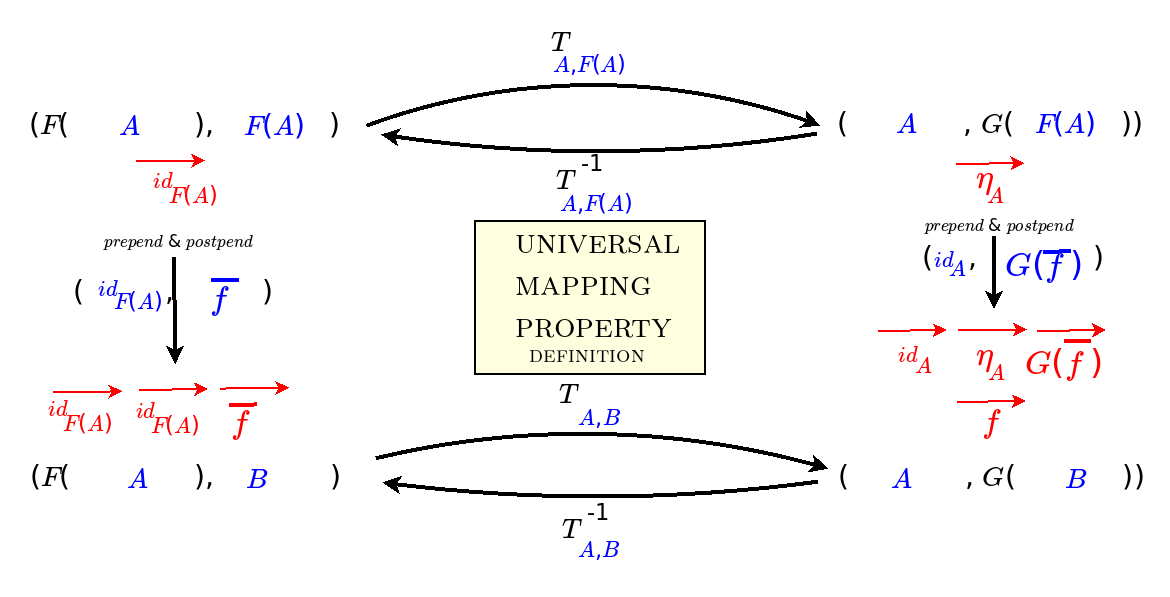2021.06.21 After more than half a year of trying, I am finally making sense of the three definitions of adjunction in terms of homsets, triangle identities, and the universal mapping property. In sharing them with Wenbo Gao, I variously corrected myself, and finally came upon the revelation I've been seeking:

Adjunctions describe how information stays the same though context changes.

For example, a light switch expresses one bit of information, which might also express whether or not to start a nuclear war.

This idea distills my observations that adjunctions separate out context, and thus strings of adjoint functors may express what I mean by divisions of everything, or perhaps, I am now thinking, alternating chains of definite (human) and indefinite (divine) perspectives. So now I am going through various examples of adjunctions to make the theory all concrete for me. I will try to classify adjoint strings.

The revelation also aligns with my contemplation of the undefinite and the definite. I think the definite arises along with knowledge and thus information and context. This brings me back to my attempts to understand the Yoneda Lemma as manifesting four levels of knowledge: whether, what, how and why.

I am also wondering how adjunctions relate to self-adjoint operators, which are central to quantum physics. I will talk today with my friend John Harland about that.

2021.06.03 I may be nearing the end of my study of the combinatorics of the Sheffer polynomials, the orthogonal polynomials {$P_n(x)$} which can be expressed as {$\sum_{n=0}^{\infty}P_n(x)t^n = A(t)e^{xu(t)}$}. In the most general case, for the Meixner polynomials, the building blocks of {$xu(t)$} and {$\textrm{ln}A(t)$} are cycles such that the starting point is either a single step {$x$} or a double step and we take some steps {$\alpha$} away and the some steps {$\beta$} to return. In working with exponential generating functions, this means that {$A(t)e^{xu(t)}$} should be counting permutations that we get by throwing labels on a set of such cycles. But I have to work out the details. There is also a combinatorial expression by Jiang Zeng in terms of growth processes of families of trees where the branches have weight {$l=-\alpha-\beta$} or {$k=-\alpha\beta$}. I need to work out the bijection that relates these two interpretations. What's clear is that the fivefold classification is contained in {$\alpha$} and {$\beta$} and the ways that they may be specialized.

I am very intrigued as to how to derive the measure associated with an orthogonal polynomial set. The Hamburger moment problem considers whether the measure exists. But in order to actually calculate the measure, evidently I have to learn how to apply the inverse Laplace transform to the moment generating function {$m(s)=\sum_{n=0}m_n\frac{s^n}{n!}$}.

{$$\mu(t)=L^{-1}\{F\}(t)=\frac{1}{2\pi i}\lim_{T\rightarrow\infty}\int_{r-iT}^{r+iT}e^{sT}F(s)ds$$}

where {$r$} is a real number so that the contour path of integration is in the region of convergence of {$F(s)$}.

2021.05.28 While thinking about Viennot's videos on the combinatorics of orthogonal polynomials, and wondering how to interpret {$(1-\alpha t)/(1-\beta t)$} in the all-encompassing Meixner polynomials, I came upon what I suspect is the deep idea that underlies the physical and cognitive understanding I seek, namely, suspension. Given the expression

{$$1 = \frac{1-\alpha}{1-\alpha} = (1-\alpha)(1+\alpha+\alpha^2+\alpha^3+\cdots)$$}

suppose that we temporarily suspend the expression by substituting {$\beta=\alpha$} in the numerator, giving

{$$1 = \frac{1-\beta}{1-\alpha} = (1-\beta)(1+\alpha+\alpha^2+\alpha^3+\cdots)$$}

Thus the suspension makes for a division into two, a choice between two different choices. One choice is to select a walk of arbitrary length. Another choice is to do nothing {$1$} or to choose an alternating contrary weight {$-\beta$}. Taking this further, we can accentuate the parameter {$\alpha - \beta$} by writing:

{$$1 = 1 + (\alpha - \beta)(1+\alpha+\alpha^2+\alpha^3+\cdots)$$}

The suspension allow us to distinguish the possibilities for degeneration. We can end the suspension by setting {$\beta$} back to {$\alpha$}, which yields the Laguerre polynomials describing the bound state, the hydrogen atom. We can further set them both to {$0$}, yielding the Hermite polynomials for the quantum oscillator, as with empty space in quantum field theory. We can restrict the difference to the imaginary dimension, and in fact, make {$\beta$} and {$\alpha$} indistinguishable by setting {$\beta = \overline{\alpha}$}. We can temporarily set {$\beta=0$}, yielding the Charlier polynomials, suggesting that they are a temporary state. Thus the momentary distinguishing of {$\alpha$} in the numerator and {$\alpha$} in the denominator yields the five states. These are the ways that a subsystem can be identified within a system. This also suggests why a perturbation is a valid way of exploring the behavior of a system. And it makes symplectic geometry relevant as that which provides the slack that allows for suspension or perturbation. So I am curious how the quadratic fetters of orthogonal polynomials might ground symplectic geometry and the other geometries - affine, projective, conformal - by distinguishing coordinate systems centered on {$1$}, {$\alpha$} and {$\beta$}.

2021.05.27 I am overviewing my questions and answers in my investigation of Sheffer polynomials.

I also corrected a big mistake that I made in investigating the Meixner-Pollaczek polynomials. I incorrectly supposed {$(1 - \alpha)(1 - \overline{\alpha})=1+|\alpha|^2$} when in fact {$(1 - \alpha)(1 - \overline{\alpha})=1-2\textrm{Re}\alpha + |\alpha|^2$}.

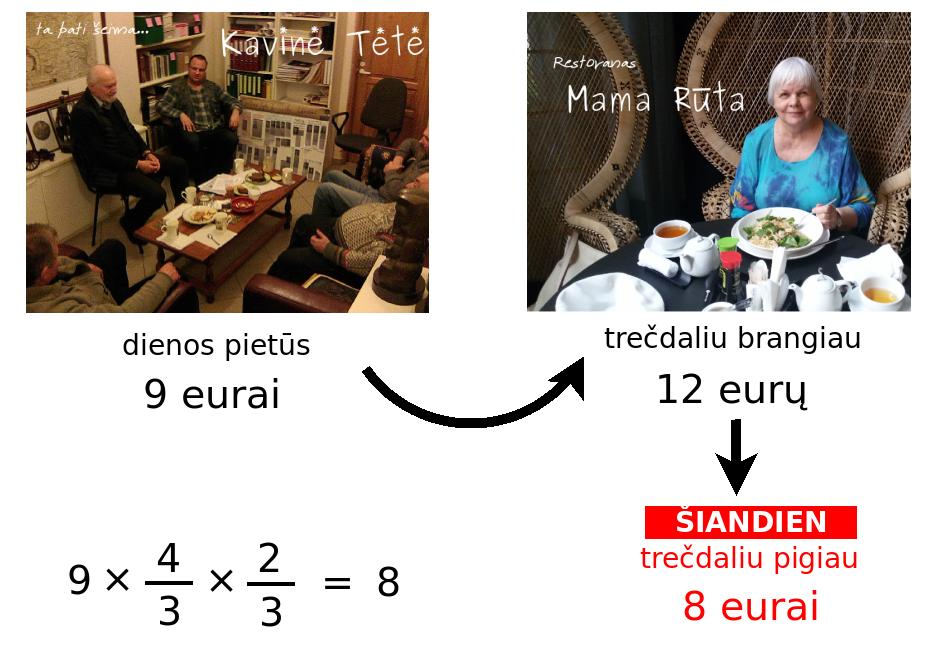
2021.05.22 I gave a talk in Lithuanian on "God's Understanding and Human's Imagination Face-to-Face at the Gates of Art". It was part of the annual conference on philosophy of art and aesthetics. This year's theme was the manifestation of religious awareness. I invite you to make sense of a machine translation into English or the Lithuanian original.

At the start of my talk, I explain our powers of imagination, how they limit us and how we transcend them. I give a mathematical example of how the imagination is lazy to think step-by-step, in other words, to do algebra. Suppose that I usually buy lunch at a cafe for 9 euros because it is one-third more at the restaurant. But suppose today that everything at the restaurant is one-third off their usual price. Where is it cheaper?

In my talk, I trace a thread from God's query, Is God necessary? to the arisal of human as the one who does not understand, to their comprehension of the asymmetry between the conditional Imaginer and the unconditional Unimagineable, to their work together towards an enlightened society which includes the self-fulfillment of each and every one. It's an overview of my philosophical vision.

2021.05.17 Every other Monday, John Harland and I talk about quantum physics. I share my work on investigating the physics in the combinatorics of orthogonal polynomials, and especially their fivefold classification, which suggests five natural bases for viewing different physical paradigms.

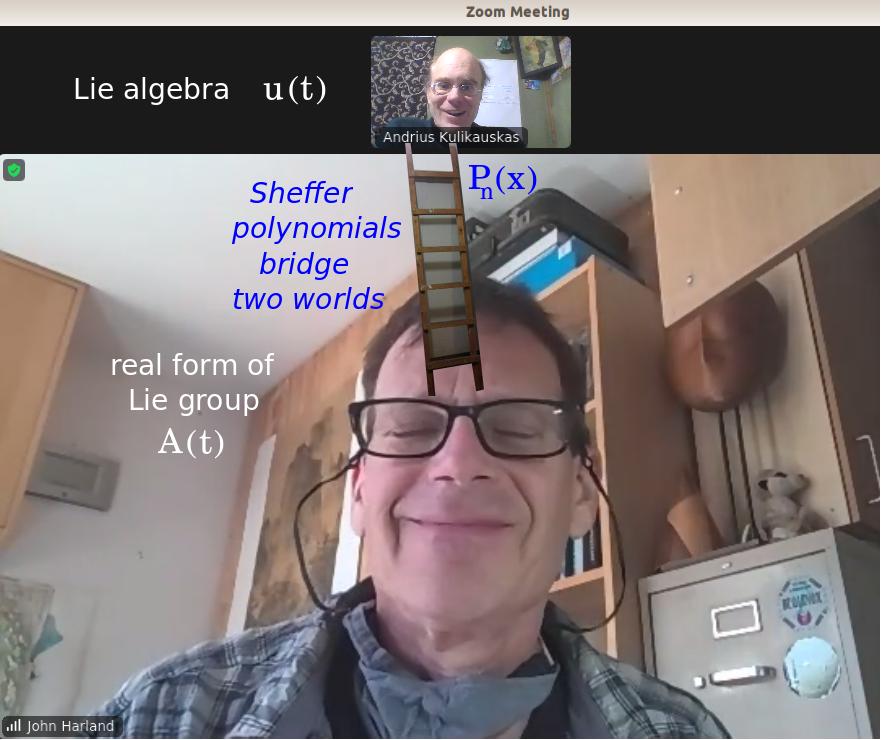
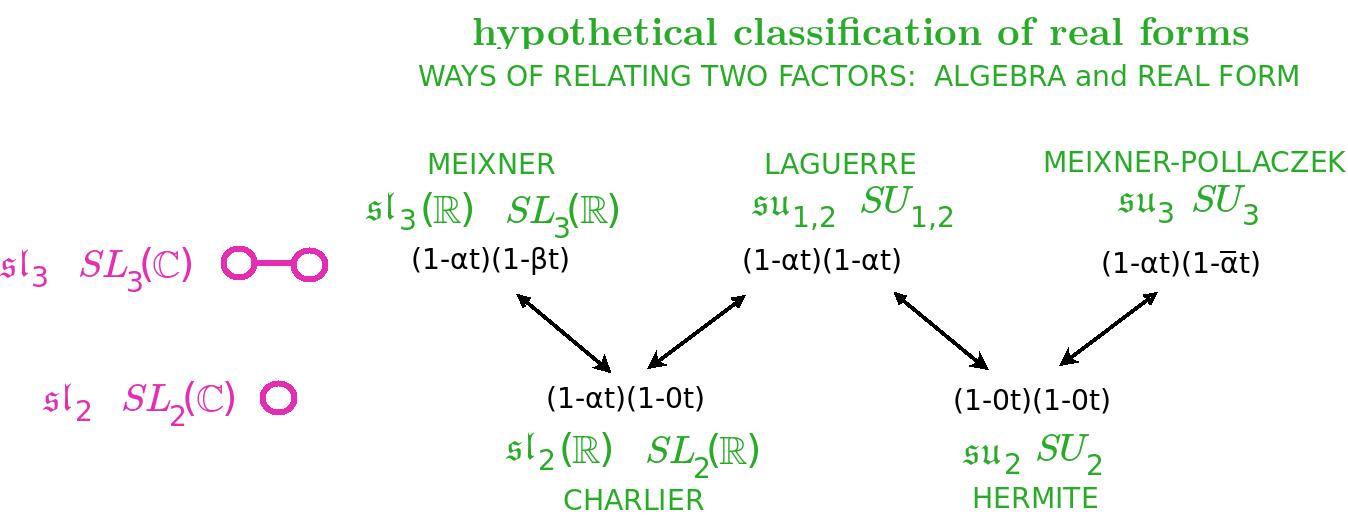
In our conversation today I realized that the equation for the Sheffer polynomials {$\sum_{n=0}^{\infty}P_n(x)t^n=A(t)e^{xu(t)}$} asserts that each such family is a bridge that links the Lie algebra {$xu(t)$} and the real form {$A(t)$} which manifests the Lie group. There are five kinds of bridges and I believe, for example, that the Hermite polynomials are the bridge in the case when the group is compact.

This suggests to me that we should look for adjoint functors that go from the group to the algebra and also back. I believe that there should be a five-adjoint-string of such functors. And I also suspect that two are related to the two real forms of {$\mathfrak{su}(2)$} (which is the node in Dynkin diagrams) and three are related to the three real forms of {$\mathfrak{su}(3)$} (which is the link in Dynkin diagrams). And that is probably just about all that Lie theory is about.

A result that encourages such thinking are these expressions:

{$A'(t) = - ct + \textrm{echo terms}$}

{$u'(t) = 1 - lt + (l^2-k)t^2 + \textrm{echo terms}$}

and also:

{$u'(t) = 1 -(\alpha + \beta) t + (\alpha^2 + \alpha\beta + \beta^2)t^2 + \textrm{echo terms}$}

By "echo terms", I mean that the higher order terms are all determined by the first few initial terms which I have indicated.

Here, in my combinatorial interpretation based on Zeng's trees, {$l$} stands for a link in a tree, {$k$} stands for a kink in a tree, {$c$} stands for a cycle of trees. In Zeng's interpretation of the moments {$L(x^n)$} in terms of permutations in {$S_n$}, {$\alpha$} stands for an ascent, and {$\beta$} stands for a descent.

It seems as if {$u'(t)$} describes the growth of a single tree, or walk in a single cycle, and {$A'(t)$} describes how trees are linked together into cycles, or how cycles of walks are combined. Thus here differentiation seems most fundamental in that it expresses the underlying growth.

I am currently working on this on pages about the Sheffer classification and the moments.

2021.05.02 Given a family of orthogonal polynomials {$\{P_n(x)\}$}, a key fact is that any polynomial {$f(x)$} can be uniquely expressed as a linear combination of them. And so, in particular, we can consider {$xP_n(x)$}, and realize that its expression may not include any {$P_k(x)$} where {$k>n+1$} or where {$k<n-1$}. If the orthogonal polynomials are monic, such that the leading term is {$x^n$} with coefficient {$1$}, this means we have {$xP_n(x)=P_{n+1}(x)+A_nP_n(x)+B_nP_{n-1}(x)$}. Here we see that the variable {$x$} comes from a single source on the left hand side but that it impacts the polynomial just above and the one just below in the hierarchy. The upshot is that the exponential possibilities are tamed by a second order recurrence relation, or alternatively, a second order differential equation. These quadratic fetters yield a fivefold classification based on the discriminant {$\sqrt{b^2-4ac}$}, much as with conics.

I am studying how to derive Sheffer's fivefold classification of orthogonal polynomials of A-type 0. This fivefold classification variously interprets the generator for walks with two kinds of step, {$\alpha$} and {$\beta$},

{$$\frac{1}{(1-\alpha t)(1-\beta t)}=(1+\alpha t+\alpha^2t^2+\cdots)(1+\beta t+\beta^2t^2+\cdots)$$}

where we may have

• no steps {$\beta = \alpha = 0$} (Hermite)
• one kind of step
  • {$\beta = 0$}, {$\alpha \neq 0$} (Charlier)
  • {$\beta = \alpha \neq 0$} (Laguerre)
• two kinds of step
  • both real: {$\beta < \alpha$} (Meixner)
  • complex conjugates: {$\beta = \overline{\alpha}$} (Meixner-Pollaczek), so that {$\alpha=a+bi$} and {$\beta=a-bi$}

But where do {$\alpha$} and {$\beta$} come from? What do they mean mathematically, physically, cognitively? I have found helpful materials including a history and exposition of Meixner's classification and treasure trove of lectures by Xavier Viennot on the combinatorics.

2021.04.25 I suspect that strings of adjoint functors may express what I mean by divisions of everything. I am thus trying to thoroughly understand the concept of adjunction in category theory, which is also important for truly mastering the Yoneda Lemma. I am therefore studying how to relate the three definitions of adjunction in terms of homsets, units and counits, and the universal mapping property. I have gone through the six ways of going from one definition to another. They all seem to serve to invert a functor in a given context. I think they also function like pushdown automata, for example, satisfying obligations, such as matching left parentheses with right parentheses. Now I am trying to work out and understand what that means for particular adjunctions such as inclusion for preorders.

2021.02.22 I am spilling the guts of quantum mechanics with combinatorial interpretations of orthogonal polynomials that arise in solutions of the Schroedinger equation.

2020.01.21 Nobel Prize laureate Duncan Haldane gives an accessible talk on Topological Quantum Matter, Entanglement, and the Second Quantum Revolution. (The Indian Institute of Technology Roorkee has a whole series of great talks.) Haldane's talk was a good introduction for me to physical effects that are some of the prerequisites to understanding the tenfold way. I was also intrigued that the Hall effect might be related to symmetric functions and, in particular, Hall-Littlewood polynomials but these are named after Edwin Hall and Philip Hall, respectively. The concept of fractional charge or fractional quanta is important, for example, in a chain of people holding hands where the hands at either end are free and possibly entangled. Similarly, the https://en.wikipedia.org/wiki/Fractional_quantum_Hall_effect fractional quantum Hall effect may express divisions of everything. Fractionally charged quasiparticles exhibit neither bosonic nor fermionic but rather anyonic statistics. This also relates to topological order in the zero-temperature phase of matter.

2020.01.11 I listened more to the The Tenfold Way by Vijay Shenoy (Part 2 of 4) about the tenfold way, the difference between the one ordinary (usual, linear) and three non-ordinary symmetries. It was helpful to see the chart and also to realize that the labels seem to be related to the classical Lie families. He talked about Hamiltonians but that part I didn't understand and should return to.

2020.01.10 At the NYCT After Meetup, Wenbo said he was interested in simplicial sets and quasicategories as he is realizing that categories are too sterile for modeling emergence. That makes sense to me from participating in Oliver's study group in Category theory and Statistics. I had sketched an adjunction for modeling statistics from which it became clear that categories need to be graded, which is to say, we need to be able to associate a probability to a morphism so that we can consider morphisms of a particular validity. In talking with Wenbo, I also realized that we need to be able to model nonassociativity, especially for composition of perspectives, and the probabilities would allow us to speak of associativity up to a certain probability. In emergence, systems or subsystems would "pop out" when they satisfied the requirements of category theory.

I told Wenbo about the conceptual frameworks, the difference between interpreting choice syntactically-asymmetrically as with observerful simplexes, or semantically-symetrically as with observerless coordinate systems. I related this to the problem of the collapse of the wave function when nature measures itself. This suggested to me that the collapse must occur when a coordinate system is introduced and thereby separates the observer from the observed. As a subsystem emerges, at a certain point it is robust enough to indicate a coordinate system, which an observer can then leverage to indicate, for example, that something did not happen. Thus the establishment of the coordinate system should be that which creates space and perhaps time, on the one hand, and that which collapses the wave function, on the other hand. Thus this would be the place to look for a relation between general relativity and quantum mechanics.

Wenbo is interested in wreath products. He shared a related excerpt from The Topos of Music by Guerino Mazzola. It had to do with time, and also to Greimas's theory of time in narrative.

2020.01.08 I'm interested in Bott Periodicity. The most helpful videos are the ones about the Tenfold Way in condensed matter research. I'm listening to The Tenfold Way by Vijay Shenoy (Part 2 of 4). The previous episode was a wonderful overview that I learned a lot from. In this episode it seems that he had to dumb it down, go back to basics, what is a group. But that's all right by me.

---

Cranky Disclaimer

You may be at risk of dismissing these pages as an online art show, science fiction, mental poetry, psychological symptoms, products of numerology, metaphysical truths, existential crises, adventures in mysticism, primordial forms... and so on and so on and so on. Just so you know!