• View
• Edit
• History
• Print

Research program Fivesome

Stone's Theorem on One-parameter Unitary Groups

I'm trying to relate Stone's theorem to orthogonal Sheffer polynomials. I hope this can help me argue that orthogonal Sheffer polynomials are the only physical solutions to the Schroedinger equation.

Sheffer polynomial sequences

Sheffer polynomial sequences {$\{P_n(x)\}$} are those with respect to which the shift operator {$T_a$} commutes with the operator Q. The shift operator is defined by {$T_aP_n(x)=P_n(x+a)$}, and the operator Q is defined by {$QP_n(x)=nP_{n-1}(x)$}. The operator Q acts like a derivative on the highest power, and the remaining terms can be thought of as echo terms, which are dependent on the highest power of each polynomial in the sequence. Thus we have {$(T_aQ-QT_a)P_n(x)=0$}.

Sheffer sequences form a group under the operation of umbral composition, which is defined as follows. Given polynomial sequences {$p_n(x)=\sum_{k=0}^{n=\infty}a_{n,k}x^k$} and {$q_n(x)=\sum_{k=0}^{n=\infty}b_{n,k}x^k$}, we define {$(p_n\circ q)(x)=\sum_{k=0}^na_{n,k}q_k(x)x^k=\sum_{n\geq k>l\geq 0}a_{n,k}b_{k,l}x^l$}.

Sheffer sequences {$\{P_n(x)\}$} have the form {$\sum_{n=0}^{\infty}P_n(x)s^n=C(s)e^{xu(s)}$}.

Orthogonal Sheffer polynomials

All orthogonal polynomials satisfy a recurrence relation of the form {$xP_n(x) = P_{n+1}(x) + A_n P_n(x) + B_n P_{n-1}(x)$}.

More specifically, Sheffer polynomials satisfy a recurrence relation of the form {$P_{n+1}(x)=[x-(ln+f)]P_n(x)-[kn(n-1)-\gamma n]P_{n-1}(x)$}. Here we can assume that {$f$} = 0 because that's equivalent to translating {$x$} to {$x-f$}.

Stone's Theorem

Stone's theorem on one-parameter unitary groups says that the equations {$\forall t\in\mathbb{R}$}: {$U_t=e^{itA}$} relate a strongly continuous one-parameter unitary group {$(U_t)_{t\in\mathbb{R}}$} with a self-adjoint operator {$A:\mathcal{D}_A\rightarrow\mathcal{H}$} where {$\mathcal{D}\subset\mathcal{H}$}.

A self-adjoint operator {$A$} on an infinite dimensional Hilbert space {$V$} (an infinite-dimensional complex vector space {$V$} with inner product) is a linear map from {$V$} to {$V$} which is its own adjoint, that is, {$\langle Ax, y\rangle = \langle x, Ay\rangle $}. In the finite-dimensional case, with an orthonormal basis, this says that {$A$} is a Hermitian matrix, it's equal to its conjugate transpose, its eigenvalues are real numbers, and it is diagonalizable. In quantum mechanics, observables are self-adjoint operators.

Adjunction

The definition of the inner product is, importantly, based on the transpose (or the conjugate transpose or quaternionic transpose). The transpose turns the left column vector into a row vector so that the resulting product of row vector times column vector gives us a sum. This sum lists (is the generating function for) all of the possible arrows from {$i$} to {$j$}. And so it codes for the information - the morphisms - coded for by a HomSet.

The adjunction equation {$\langle Ax, y\rangle = \langle x, Ay\rangle $} indicates that {$(Ax)^Ty = x^TAy$}, which means that {$x^TA^Ty = x^TAy$} and {$A^T=A$}. And here the transpose may be replaced by the conjugate transpose.

Building and interpreting space

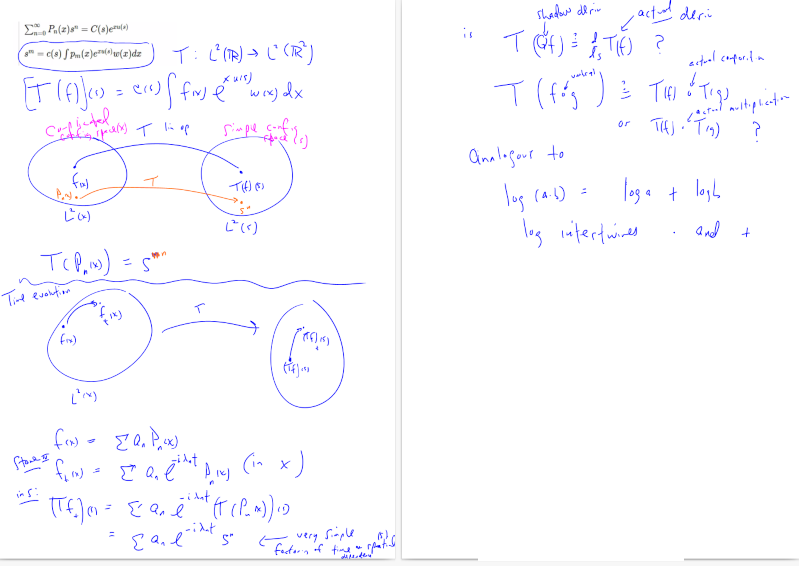
{$\sum_{n=0}^{\infty}P_n(x)s^n=C(s)e^{xu(s)}$}

{$P_n(x) = C(s)e^{xu(s)}|_{s^n \textrm{term}} = \frac{1}{n!}\frac{\textrm{d}^n}{\textrm{ds}^n}|_{s=0}C(s)e^{xu(s)}$}

This yields Bell numbers as the ways of building space.

Then the constraints on {$u(s)$} and {$C(s)$} from orthogonality give the five ways of interpreting space. The constraints mean that we have simply three independent variables which relate to links and kinks and can express three dimensions of space as related by {$s$} being constant, linear or quadratic. This relation then pulls down the echo terms. And time is included trivially as the base case.

{$u'(s)=1 + (\alpha + \beta)s + (\alpha^2 + \alpha\beta + \beta^2)s^2 + \textrm{echo terms}$}

{$C'(s)=-\gamma s + \textrm{echo terms}$}

{$f(x,t) = \sum\frac{a_n}{n!}\frac{\textrm{d}^n}{\textrm{ds}^n}(C(s)e^{u(s)x-i\lambda_n t})|_{s=0}w(x)$}

This is simply compatible with Stone's theorem.

{$\frac{\textrm{d}}{\textrm{ds}}(C(s)e^{xu(s)+K}) = (c'(s) + x c(s)u'(s)) e^{xu(s)+K}$}

Another idea:

{$s^mN_m = C(s)\int P_m(x)e^{xu(s)}w(x)dx$}

Literature

Duchamp et al. One-Parameter Groups and Combinatorial Physics

How are Sheffer polynomials related to Lie theory?

What's up with Wick's theorem?

Why is the Gaussian so pervasive in mathematics?

Tom Copeland. Cycles and Heat: Hermite-Sheffer Evolution Equations

Tom Copeland. The heat equation, the quantum harmonic oscillator, the Hermite polynomials, and Gaussian integral transforms