• View
• Edit
• History
• Print

I am overviewing the questions that I am asking and the answers that I am finding in my investigation to interpret the fivefold classification of Sheffer polynomials.

I am seeking a combinatorial and algebraic understanding of the classification that would explain how the allowable polynomials manifest conceptual and physical paradigms.

Pieces of the Puzzle

I am listing out various pieces of the puzzle.

Sheffer polynomials

Sheffer polynomials are orthogonal polynomial sets {$\{P_n(x)\}$} of the form

{$$\sum_{n=0}^{\infty}P_n(x)t^n=A(t)e^{xu(t)}$$}

Recurrence relations

All orthogonal polynomials satisfy a recurrence relation of the form

{$$xP_n(x) = P_{n+1}(x) + Q_n P_n(x) + R_n P_{n-1}(x)$$}

More specifically, Sheffer polynomials satisfy a recurrence relation of the form (compare with Kim and Zeng)

{$$P_{n+1}(x)=[x-(ln+f)]P_n(x)-[kn(n-1)-\gamma n]P_{n-1}(x)$$}

Here we can assume that {$f$} = 0 because that's equivalent to translating {$x$} to {$x-f$}.

Solution from recurrence relations

As shown by Galiffa and Riston, who expand the infinite series {$A(t)e^{xu(t)}$}, this recurrence relation is determined by {$a_1$}, {$a_2$}, {$u_2$}, {$u_3$}. Namely,

{$f=-a_1$}, {$l=-2u_2$}, {$k=4u_2^2-3u_3$}, {$\gamma = a_1^2-2a_2+2a_1u_2$}

(Noting with care for {$k$} and {$\gamma$} that Galiffa and Riston use the expression {$-[(c+d)n + dn^2]$} whereas Kim and Zeng use {$-[\mu_1 \mu_2 n(n-1) + \beta\mu_1\mu_2 n]$}

We can turn these equations around to give combinatorial meaning to the initial terms of {$A(t)$} and {$u(t)$}.

{$a_1 = -f$}, {$a_2 = \frac{\gamma +fl-f^2}{2}$}, {$u_2=\frac{-l}{2}$}, {$u_3=\frac{l^2-k}{3}$}. (FIX THIS! see Sheffer classification)

We can suppose {$f=0$} by considering the translation of {$x$} to {$(x-f)$}. Then {$a_2=\frac{\gamma}{2}$}. This yields:

{$$A(t)=1 - \frac{\gamma}{2}t^2 + a_3t^3 + a_4^t4 + \cdots$$}

{$$u(t)=t - \frac{l}{2}t^2 + \frac{l^2-k}{3}t^3 + a_4^t4 + \cdots$$}

Note that the higher order terms are not relevant, in that they are determined by the initial terms. Note also that the translation would only have affected {$A(t)$}, which is for compactness, but not {$u(t)x$}, which expresses the Lie algebra.

Then we get the most natural and profound expressions for {$u'(t)$} and {$A'(t)$}.

{$A'(t) = -\gamma t + \textrm{echo terms}$}

{$u'(t) = 1 - lt + (l^2-k)t^2 + \textrm{echo terms}$}

I mean by "echo terms" that the higher order terms are completely determined by the initial terms and have no independent significance.

We can choose to write {$u'(t) = \frac{1}{(1-\alpha t)(1 - \beta t)} = 1 + (\alpha + \beta)t + (\alpha^2 + \alpha\beta + \beta^2)t^2 + \textrm{echo terms}$}

Then we have {$l=(-\alpha)+(-\beta)$} and {$k=(-\alpha)(-\beta)$} and {$(1-\alpha t)(1-\beta t) = 1+lt+kt^2$}.

Nand and Nor

Note that we can interpret {$l$} to mean {$\textrm{NAND(A,B)}$}, for (NOT (A AND B) = (NOT A) OR (NOT B), and we can interpret {$k$} as {$\textrm{NOR(A,B)}$}, for (NOT (A OR B) = (NOT A) AND (NOT B). NAND and NOR are the two logical operators from which all other operators can be derived. And algebraically, we get an interesting logic where NAND(A,B) = (-A)(-B) = AB = AND(A,B). I should study this logic.

Differential equation

{$A(t)$} and {$u(t)$} satisfy the differential equations below, where {$l$}, {$k$}, {$\gamma$} are taken from the recurrence relation above.

{$$u'(t)=\frac{1}{1+lt+kt^2}=\frac{A'(t)}{\gamma tA(t)}$$}

It is straightforward to solve for {$A(t)$} upon noting that {$\frac{\textrm{d}}{\textrm{dt}}\textrm{ln}A(t)=\frac{A'(t)}{A(t)}$}. I am still working on how to solve for {$u(t)$}. Apparently, it is more sophisticated. I think it depends on inverting {$t(u)$} and noting that {$\frac{\textrm{dt}}{\textrm{du}}=\frac{1}{u'(t)}$}.

In the differential equations above, we can factor the quadratic and rewrite them as follows:

{$$u'(t)=\frac{1}{(1-\alpha t)(1-\beta t)}=\frac{1}{1+lt+kt^2}=\frac{A'(t)}{\gamma tA(t)}$$}

In the most general case, the solution gives the Meixner polynomials.

{$u(t)$}	{$\textrm{ln}A(t)$}	{$A(t)$}	{$e^{x(u(t))}$}
{$\frac{1}{\beta - \alpha}\textrm{ln}(1-\alpha t)+\frac{1}{\alpha - \beta}\textrm{ln}(1-\beta t)$}	{$\frac{\gamma}{\alpha \beta}[\frac{\alpha}{\alpha - \beta} \textrm{ln}(1-\beta t) - \frac{\beta}{\alpha - \beta} \textrm{ln}(1 - \alpha t)]$}	{$(\frac{(1-\beta t)^\alpha}{(1-\alpha t)^\beta})^{\frac{\gamma}{\alpha\beta(\alpha - \beta)}}$}	{$(\frac{1-\beta t}{1-\alpha t})^{\frac{x}{\alpha-\beta}}$}

Fivefold classification

Various specializations of the Meixner polynomials yield a fivefold classification.

polynomials	{$\alpha$}, {$\beta$}	{$u'(t)$}	{$u(t)$}
Hermite	{$\alpha=\beta$}, {$\beta=0$}	{$1$}	{$t$}
Charlier	{$\alpha\neq\beta$}, {$\beta=0$}	{$\frac{1}{1-\alpha t}$}	{$-\frac{1}{\alpha}\textrm{ln}(1-\alpha t)$}
Laguerre	{$\alpha=\beta$}, {$\beta\neq 0$}	{$\frac{1}{(1-\alpha t)^2}$}	{$\frac{t}{(1 - \alpha t)}$}
Meixner	{$\alpha \neq \beta$}, both real, nonzero	{$\frac{1}{(1-\alpha t)(1-\beta t)}$}	{$\frac{1}{\beta - \alpha}\textrm{ln}(1-\alpha t)+\frac{1}{\alpha - \beta}\textrm{ln}(1-\beta t)$}
Meixner-Pollaczek	{$\alpha=\overline{\beta}$}, complex conjugates, nonzero	{$\frac{1}{(1-\alpha t)(1-\overline{\alpha} t)}$}	{$\frac{1}{\overline{\alpha} - \alpha}\textrm{ln}(1-\alpha t)+\frac{1}{\alpha - \overline{\alpha}}\textrm{ln}(1-\overline{\alpha} t)$}

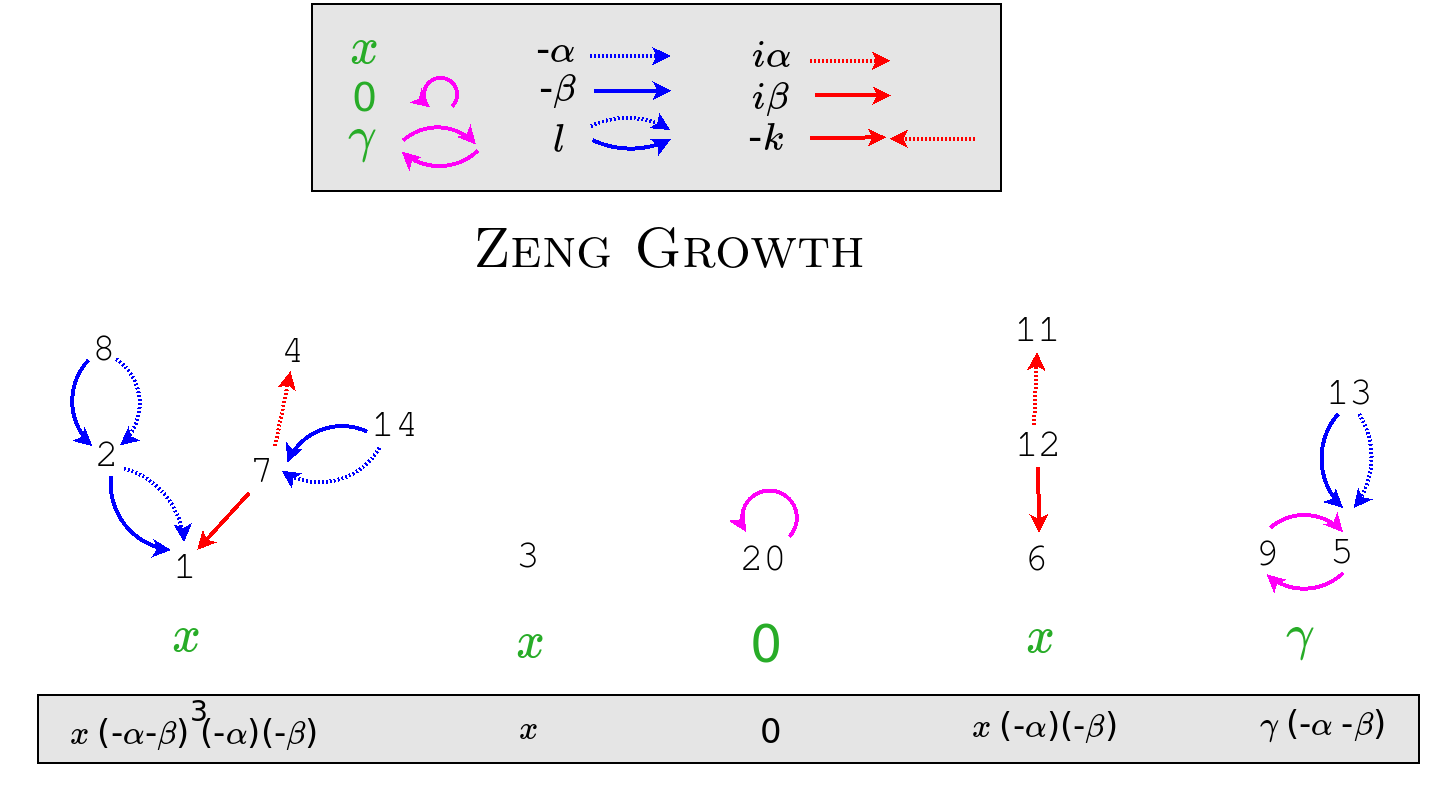
Zeng growths

Jiang Zeng worked out a combinatorial interpretation of the Sheffer polynomials that is extremely contentful. He and Dongsu Kim write out the recurrence formula much like this:

{$$P_{n+1}(x)=[x-((u_3+u_4)n+a_1b_1)]P_n(x)-n[n+b_1-1](u_1u_2))P_{n-1}(x)$$}

It turns out that their expression is overly subtle for our purposes. It is what they need to explain the combinatorics of linearization. Our simpler recurrence relation has everything needed for their combinatorial interpretation of the Sheffer polynomials and even their orthogonality.

{$$P_{n+1}(x)=[x-(ln+f)]P_n(x)-[kn(n-1)-\gamma n]P_{n-1}(x)$$}

{$l=u_3+u_4$} and {$k=u_1u_2$} and we know that {$l=-\alpha-\beta$} and {$k=\alpha\beta$}. Note that the weights {$u_1$}, {$u_2$}, {$u_3$}, {$u_4$} are simply combinatorial place holders. So for our purposes we can set {$u_1=u_3=-\alpha$} and {$u_2=u_4=-\beta$}. And we suppose {$f=0$}, so we can assume {$a_1=0$}.

---

---

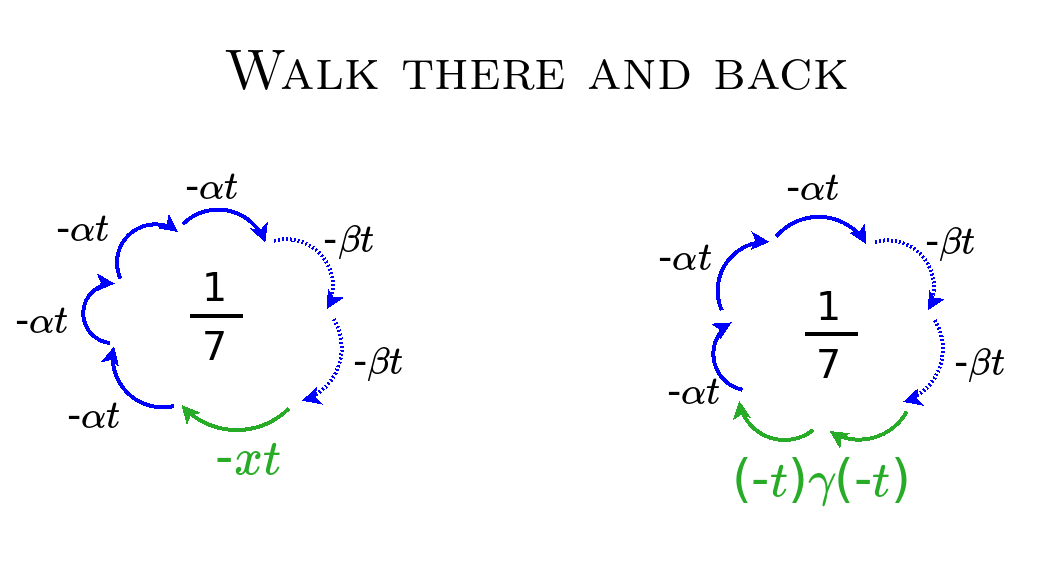
Walks somewhere and back

Zeng's interpretation comes from the recurrence relation. But we can get another recurrence relation by considering the logarithm of the generating function for the Meixner polynomials. Note that {$-\textrm{ln}(1-\alpha t)=\alpha t + \frac{1}{2}\alpha^2 t^2 + \frac{1}{3}\alpha^3 t^3 + \cdots$} and that {$\beta^{k+1}-\alpha^{k+1}=(\beta-\alpha)(\beta^k+\beta^{k-1}\alpha + \dots + \beta\alpha^{k-1} + \alpha^k)$}.

{$$\textrm{ln}A(t)+xu(t)=$$} {$$-t(x)+\frac{(-t)^2}{2}(x(\beta + \alpha) - \gamma)+\frac{(-t)^3}{3}(x(\beta^2 + \beta\alpha + \alpha^2) - \gamma(\beta+\alpha)) +$$} {$$\frac{(-t)^4}{4}(x(\beta^3 + \beta^2\alpha + \beta\alpha^2 + \alpha^3) - \gamma(\beta^2 + \beta\alpha + \alpha^2))+\dots$$}

---

---

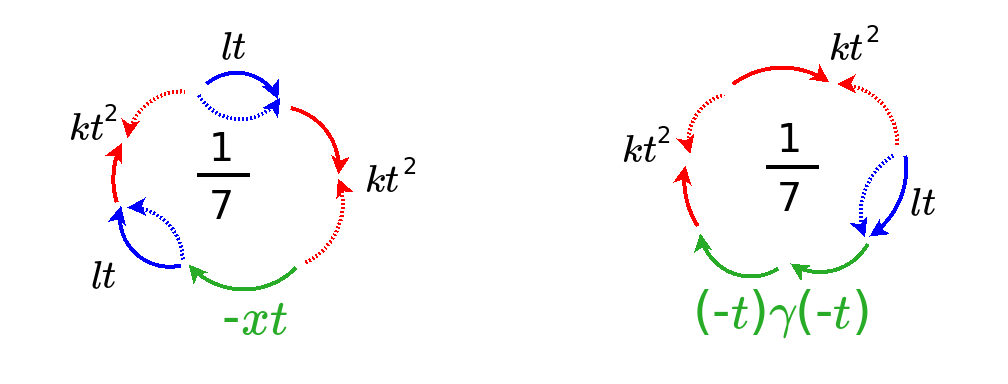
We can express the walk in {$\alpha$} and {$\beta$} in terms of {$l$} and {$k$}.

{$$\sum_{k=0}^{n}\alpha^k\beta^{n-k}=\sum_{j=0}^{\frac{n}{2}}(-1)^{n-j}l^{n-2j}k^j\binom{n-j}{j}$$}

Whereas {$\alpha$} and {$\beta$} were strictly ordered, here we have all possible ways of ordering {$l$} (of length {$1$}) and {$k$} (of length {$2$}). Note that if there are {$j$} segments with weight {$k$} of length {$2$}, then there are {$n-2j$} segments with weight {$l$} of length {$1$}, and so there are {$n-j$} segments in all, which is why we have {$\binom{n-j}{j}$} orderings.

---

---

Moments

{$$L(x^n)=\sum_{\sigma\in S_n}(-\alpha)^{a\sigma} (-\beta)^{d\sigma} 0^{fix\sigma}(\frac{-\gamma}{\alpha\beta})^{cycle\sigma}$$}

Schroedinger equation

Suspension

Given the expression

{$$1 = \frac{1-\alpha}{1-\alpha} = (1-\alpha)(1+\alpha+\alpha^2+\alpha^3+\cdots)$$}

temporarily substitute {$\alpha=\beta$} in the numerator

{$$1 = \frac{1-\beta}{1-\alpha} = (1-\beta)(1+\alpha+\alpha^2+\alpha^3+\cdots)$$}

and then consider various degenerate cases such as {$\beta=0$}, {$\beta=\overline{\alpha}$}, {$\beta=\alpha$} and {$\alpha=0$}.

---

Weights

• Where do the weights come from?
• How do the weights relate to the generating functions for {$A(t)$} and {$e^{xu(t)}$}?
• Write out the weights in terms of Taylor series.
• What is the combinatorial interpretation of the weights?

Moments

• What do the moments say about weights?

Generating functions

• Calulate the "echo terms" for the generating function for {$u'(t)$} in terms of {$l$} and {$k$} and find their combinatorial interpretation.
• Interpret the generating function for the Meixner polynomials, focusing on the expression for the exponential, {$\textrm{ln}A(t)+u(t)$}.
• Given the generating function for the Meixner polynomials, set {$\beta=\overline{\alpha}$} to get the generating function for the Meixner-Pollaczek polynomials.

Differential equation

• Derive the differential equation for {$u(t)$} in the Sheffer polynomials.
• Write up the derivation of the differential equation for {$A(t)$}.
• Derive the differential equation for the Jacobi polynomials.

Classical orthogonal polynomials

• How do the Sheffer polynomials relate to the Jacobi polynomials?
• What differential equation do the Sheffer polynomials satisfy?

Lie theory

• How do the functions {$u(t)$} and {$A(t)$} relate to Lie algebras and real forms?
• How do these functions relate to matrix Lie algebras?
• What is the meaning of the functions {$u'(t)$} and {$A'(t)$}?