• View
• Edit
• History
• Print

Causal Links & Causal Kinks

I'm investigating the implications for quantum physics of the configurations which arise in the combinatorial interpretation of Isador Sheffer's fivefold classification of orthogonal polynomials. In particular, his fivefold classification can be understood in terms of a cognitive framework for decision making, the division of everything into five perspectives, which presents causality in terms of causal links ("every cause has had its effect") and causal kinks ("not every cause has had its effects").

I note these relevant publications:

• Isador M. Sheffer. Some properties of polynomial sets of type zero. 1939. Sheffer's fivefold classification of orthogonal polynomials. I don't have access to this paper, though.
• Theodore Chihara. An Introduction to Orthogonal Polynomials. 1978. The most helpful statement of the fivefold classification that I found so far, thanks to Kim and Zeng's paper.
• X. G. Viennot, Une theorie combinatoiredes polynomes orthogonaux generaux, Notes deconferences donnees a l’UQAM, Montreal, 1983
• Xavier Viennot's website
• The Art of Bijective Combinatorics Part IV. A combinatorial theory of orthogonal polynomials and continued fractions. Chapters 7-10
  • Chapter 5. Orthogonality and exponential structures.
  • Xavier Viennot. Chapter 5c: Tableaux and Orthogonal Polynomials
• In 1990, J. Zeng, Linearisation de produits de polynomes de Meixner, Krawtchouk, et Charlier, SIAM J.Math. Anal.,21 (1990), 1349–1368.
• In 2001, Dongsu Kim and Jiang Zeng published A Combinatorial Formula for the Linearization Coefficients of General Sheffer Polynomials. Here I found their combinatorial interpretation of the Sheffer polynomials and also their orthogonality equations.
• Daniel Galiffa, Tanya Riston. An elementary approach to characterizing Sheffer A-type 0 orthogonal polynomial sequences. 2015.
• Waleed A. Al-Salam. Characterization Theorem for Orthogonal Polynomials. In Orthogonal Polynomials: Theory and Practice Edited by Paul Nevai, 1990. The classification of Sheffer polynomials is discussed on pages 1-4, which are available in the free preview.

The Sheffer family satisfies the recurrence relation below, with initial polynomials {$P_{-1}=0$} and {$P_0=1$}:

{$$P_{n+1}(x) = (x - (nl + f)) P_n(x) - n(nk + c) P_{n-1}(x)$$}

I will be writing it like this to help remember that {$l$} is the weight for links, {$k$} for kinks, {$f$} for fixed points (self-entangled trees), {$c$} for cycles (trees). Here {$x$} is taken without coefficient and so the resulting polynomials are all monic. A coefficient can always be introduced by substituting {$x=cy$}. {$f$} is trivial in that it corresponds to a translation of {$x$} and thus can be set as zero.

---

---

Sheffer classifies orthogonal polynomials whose generating function has the form

{$$A(t)e^{xH(t)}=\sum_{n=0}^{\infty}P_n(x)t^n$$}

where {$A(t)=\sum_{n=0}^{\infty}a_nt^n$}, {$a_0=1$}, {$H(t)=\sum_{n=1}^{\infty}h_nt^n$}, {$h_1=1$}. Then the recurrence relation is determined by the values {$a_1$}, {$a_2$}, {$h_2$}, {$h_3$}. In particular, {$f=-a_1$}, {$l=-2h_2$}, {$c=a_1^2-2a_2+2a_1h_2$}, {$k=4h_2^2-3h_3$}.

There is a fivefold classification of polynomials based on the cases

• {$h_2^2=h_3=0$}
• {$h_2^2=\frac{3}{4}h_3$}
• {$h_2^2=h_3$}
• {$h_2^2>h_3$}
• {$h_2^2<h_3$}

Alternatively

• {$k=0$} These are limiting cases of the polynomials further below.
  • {$l=0$} Hermite polynomials. The quantum oscillator. The background assumption for the quantum field. Weight function is basically the standard normal probability density function.
  • {$l\neq 0$} Charlier polynomials. Weight function is the discrete mass distribution with mass {$\frac{a^j}{j!}$} at the integer point {$j=0,1,2,3\cdots$}, and in the case {$a>0$} it is the Poisson distribution. Related to the Poisson process (average time between events is given but events are random) and to Markov birth processes (with no deaths). Oscillator realized in the Weyl algebra, the ring of differential operators with polynomial coefficients, also known as the symplectic Clifford algebra, used by Weyl to study the Heisenberg uncertainty principle. Weyl and Clifford algebras can be unified as even and odd dimensions of a superalgebra. Quantum oscillator based upon the algebra of supersymmetric quantum mechanics, the Heisenberg-Weyl superalgebra.
• {$k>0$}, {$k+c>0$}, {$l$} and {$f$} real
  • {$l^2-4k=0$} Laguerre polynomials. Hydrogen atom. Bound states. Weight function {$x^ae^{-x}$}.
  • {$l^2-4k>0$} Meixner polynomials of the first kind. Also known as Hahn polynomials. Weight function is the distribution step function whose jumps are {$\frac{(\alpha)_x(\beta)_x}{(\gamma)_x x!}$} at {$x=0,1,2,\cdots$}, related to the hypergeometric series, making use of the Pockhammer symbol {$(q)_n=q(q+1)\cdots (q+n-1)$} and {$(q)_0=1$}. A special case is the Krawtchouk /Kravchuk polynomials, which are not positive-definite orthogonal, and can be used to definite something like a finite Fourier transform, and used to describe irreducible represetation of su(2) and SU(2). Another special case is the discrete Chebyshev polynomials, used in least square fitting, known as Gram polynomials. Another special case is Pasternak's polynomial. The Meixner polynomials of the first kind are important for describing Markov birth and death processes, thus presumably creation and annihilation of particles. When {$h=0$} these are the discrete Laguerre polynomials.
  • {$l^2-4k<0$} Meixner polynomials of the second kind, also known as Meixner-Pollaczek polynomials. Weight function is {$|\Gamma(\frac{1}{2} + ix)|^2e^{(2\phi - \pi)x}$}. (Note that the Gamma function {$\Gamma(z)=\int_{0}^{\infty}x^{z-1}e^{-x}\textrm{dx}$} is defined on all complex numbers except the nonpositive integers, which basically complements the discrete weight.) Related to a particular case where the moments are the Euler numbers of order j defined by {$\textrm{sech}^j t$}. Also, when {$l=0$} we get symmetric polynomials. There is a connection between the symmetric Meixner–Pollaczek polynomials, Pn(1/2)(x/2,π/2) and some identities for symmetric elements in the Heisenberg algebra. Meixner-Pollaczek polynomials bridge the Laguerre polynomials and Hermite polynomials, which are limiting cases, and there are more. Meixner-Pollaczek polynomials (case {$\lambda = 1/2$}) are generalized by the Pollaczek polynomials, whose asymptotic investigation may yield clues concerning the behavior of orthogonal polynomials when the weight function fails to satisfy certain integrability conditions. Perhaps they may help understand renormalization?

For Zeng's interpretation, we can write the recurrence relation:

{$$P_{n+1}(x) = (x - αβ - nμ) P_n(x) - nθ(β + n - 1) P_{n-1}(x)$$}

In this recurrence relation, the coefficient μ of {$nP_n(x)$} weights links (single edges) and the coefficient θ of {$ n^2 P_{n-1}(x)$} weights kinks (double edges) in a tree. Note that relating to {$P_{n-1}(x)$} with a kink has us go backwards in time to a previous state, and that momentum expresses the obligation which we fulfill. (Position and momentum can be switched accordingly. What does the Heisenberg uncertainty principle say about the relationship between links and kinks?) The recurrence relation expresses a fundamental fact about the world, double causality, as with the fivesome. Also, double causality grounds slack, complex numbers, a triple perspective, and symplectic geometry.

Note also that the roots of the trees arise without context as self-links or self-kinks, whereas the other links and kinks of a tree have the tree as a context.

How is the generating function related to trees and walks?

We get special cases by setting {$α$}, {$β$}, {$μ$}, {$θ$}:

Physicist Hermite polynomials	harmonic oscillator	{$H_{n+1}(x) = xH_n(x) - nH_{n-1}(x)$}	{$α = μ = 0$}, {$β = 1/θ$}, and let {$θ\rightarrow 0$}	root {$=x$}, pair of roots {$=-1$}
Laguerre polynomials	hydrogen atom	{$L_{n+1}(x) = (x - β - 2n)L_n(x) - n(β + n - 1)L_{n-1}(x)$}	{$α = θ = 1$}, {$μ = 2$}	presumably many terms cancel out
Chebyshev polynomials of the second kind	infinite well	{$U_{n+1}(x) = 2x U_n(x) - U_{n-1}(x)$}	{$x=2y$}, {$α=μ=0$}, {$β = 1/θ$}, and let {$θ\rightarrow 0$}	...

---

---

---

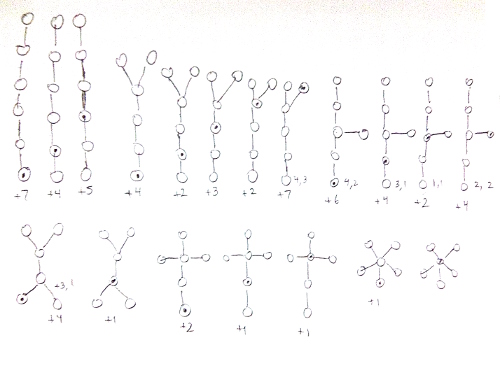
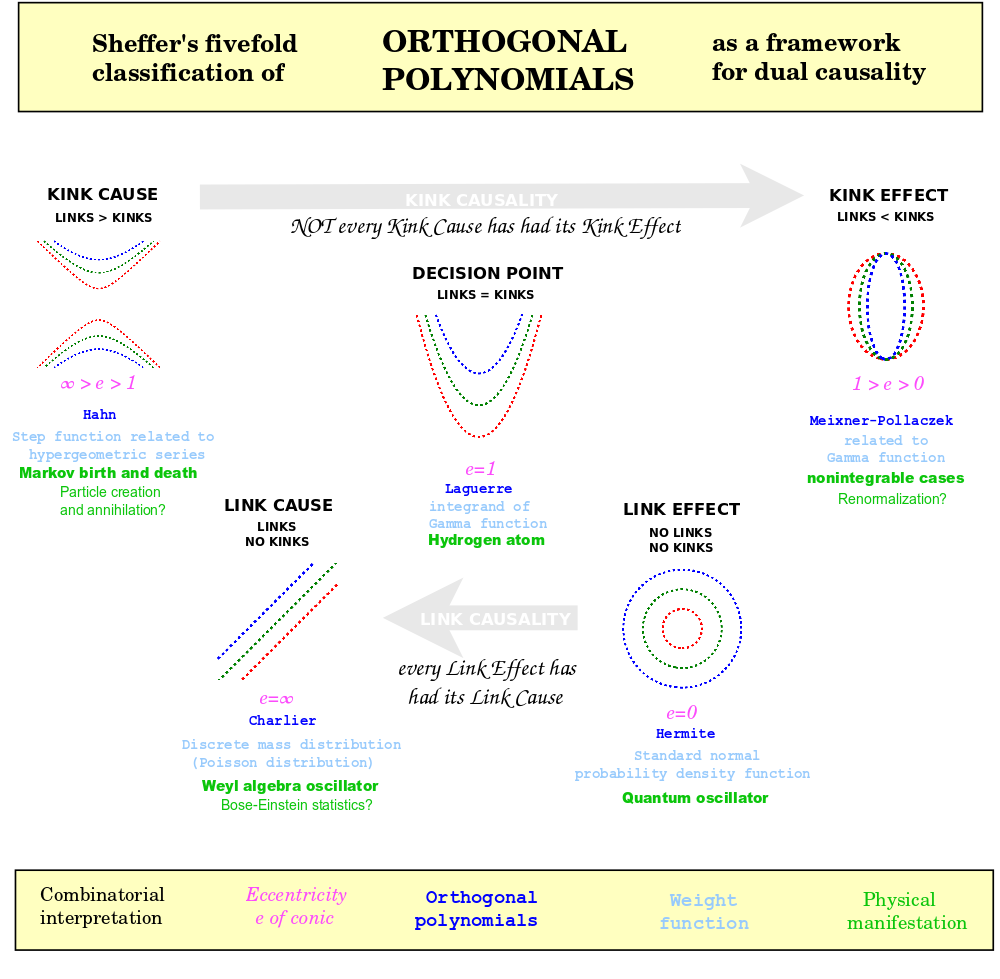
I would give some physical sense of their intepretation by restating it as follows. Let S be the set {1, 2, ... , n}. The orthogonal polynomial Pn is a sum of weighted terms. Each weighted term is the product of multiplicative weights. Each term signifies a way that a system of n vertices can evolve as a set of rooted trees. You construct the set of rooted trees by going through the set S in order and making the following decisions:

A vertex can be included or set aside. If it is included, then:

• It may be included in an existing rooted tree by adding a new edge and vertex from any existing vertex. (Consequently, in general, trees tend to show their growth with increasing numbers along any path away from the root.) (Weight: integer {$-μ$} ).
• It may be used as the root for a new tree. (Weight: variable {$x$})
• It may be used as the root for a new tree (Weight: integer {$β$}) which includes an extra loop from the root to the root. (Weight: integer {$-α$}) (By Chihara's comment, this possibility simply expresses an arbitrary translation of {$x$}, and so we can set {$α=0$} and ignore this possibility entirely. Alternatively, we can trivially allow for an arbitrary translation, retain {$α$} and include this trivial self-entanglement as a trivial possibility.
• It may be set aside for later...
• It may be paired with any of the vertices that has been set aside:
  • to add to an existing rooted tree a new edge further extended by a second new edge. (We first add the latest vertex and then add the vertex which had been set aside. Thus this violates the outward growth of the numbers.) (Weight: integer {$-θ$}).
  • or to be the roots for two new rooted trees (Weight: integer {$β$}) that are linked to each other by edges (Weight: integer {$-θ$}).

---

---

A Good Example

I think that we truly don't know for sure what Jesus meant in about a third of his sayings. I have never heard any preacher admit as much. Anyways, I feel an immense encouragement when I manage to crack one of his riddles, as I think I have here. More than twenty years ago, it struck me that he was saying, "This is my bread, and by all rights, it is destined to be my body, and thus it truly is my body, as regards the usual worldly causality. And yet I can intervene, I can decline to eat it, and so give my body to you for you to accept and to eat." That seems the honest, straightforward, childlike way of hearing him at face value, his very words. This is the reading that makes his action truly enlightening, instructive, exemplary, symbolic and meaningful. Instead, we are insistently taught that we are to take him mystically, which is to say, that we can't hope to comprehend this divine mystery, as if such ignorance was our highest purpose. I am just realizing that the Unimagineable may be the most fruitful way to think of God. All the same, we can't appreciate that by pretending to not understand. As regards this saying of Jesus, I believe my comprehension is a causal kink that spans two thousand years from him to me.

---

On Second Thought

Kinks make it possible for us to have second thoughts and more.

---

It's All Right to Think Twice

Two of my favorite songs growing up were "She Loves You" by the Beatles and "Don't Think Twice, It's All Right" by Bob Dylan. They both play with causal kinks. And they talk past each other! So I concoct a superposition of Bob Dylan's disentanglement and the Beatles' reentanglement. That's a song waiting to be sung: "It's All Right to Think Twice".

Our family's very first record was "The Best of Peter, Paul and Mary: Ten Years Together". Another ten years after that, I withstood a great causal kink when, as a freshman at the University of Chicago, my roommate Joe Sochor played Bob Dylan. It was a jolt to learn about this giant of music, to realize that he was the author of my favorite song, and to hear the original, so real and true.

---

Various notes

Compare with Chihara's recurrence relation, in which we have {$\beta - 1$}, which suggests that {$\beta$} is expressing extra trees, above and beyond the initial one, but then why are we subtracting 1 rather than adding 1 ?

All of the vertices that get set aside have to get used up. These pairs can be thought of as "entanglements". They function like a pushdown automata, a very primitive form of memory, as with a particle and anti-particle.

Basically, we have three kinds of trees:

• A free tree - which gets weight {$x$} - like empty space.
• A tree with self-entangled roots.
• A pair of trees whose roots are entangled with each other.

And all trees can have entanglements within themselves. But they are all drawing vertices from the same pool {$S$}.

So these are rules for evolving the possible "configurations" including their entanglements within (pairs of vertices) and also without (pairs of roots).

Furthermore, the paper interprets what happens when these different orthogonal polynomials get multiplied together and integrated over so that they vanish or not. The combinatorics has to do with summing over all permutations and then we set {$θ = u_1 u_2$} and {$μ = u_3+u_4$}. Then the powers of the various weights {$α$}, {$β$}, {$u_1$}, {$u_2$}, {$u_3$}, {$u_4$} count various attributes of the permutations, such as number of decents and ascents.

Now I need to consider how these collections of trees reduce to the special cases of interest, for example, the harmonic oscillator, the infinite well, the hydrogen atom, the radial function.

One of the authors, the mathematician Jiang Zeng, is part of a team of collaborators working with physicist Mohamed Jalel Atia, who is in Saudi Arabia, to champion the use of orthogonal polynomials in quantum mechanics. So maybe I will write up my basic ideas and then reach out to them.

Also, there seems to be a useful and inexpensive book on orthogonal polynomials that I will purchase:

Also, I am learning how to use Sage , which is an open source software similar to Mathematica. They have a module with which I should be able to create trees, generate, enumerate, manipulate, count them, etc. Then I can compare the sequences I get with those in the Online Encyclopedia of Integer Sequences.

What is the meaning of Sheffer sequence and what are the implications for physics?

Note that the cause (hyperbola, line) relates two cones but the decision point only one cone and the effect (ellipse, circle) only one cone.

To Do

• Understand how Sheffer's generating function {$A(x)e^{B(x)}$} relates to Lie groups and Lie algebras.
• Understand how Sheffer's generating function's properties get expressed as the weights in the recurrence relation.
  • For the Sheffer polynomials, is {$d^2-4g$} the discriminant {$b^2-4ac$}? And is {$a=1$} because we have a monic polynomial? So what does it mean physically and combinatorially if {$a\neq 1$}?.
• Understand how the rook polyonomial interpretation of the Laguerre polynomials expresses the perfect balancing of links and kinks.
• Understand Kim and Zeng's combinatorial interpretation of orthogonality.
• Understand how kinks can be understood to reverse the causality of links, especially when there are no links. And then what are the implications that the dimension in that case must be even?
• Understand, interpret and relate the relativistic account of the hydrogen atom.
• Find a combinatorial interpretation for the spherical harmonics.
• Consider what the trivial translation from {$x$} to {$x-a$} means for relativity.
• Consider examples of how trees cancel away to yield particular families of orthogonal polynomials

The Morals of the Story?

---

Some notes

{$$P_{n+1}(x) = (x - (dn + f)) P_n(x) - n(gn + h) P_{n-1}(x)$$}

My research notes are at: Research.OrthogonalPolynomials and see also Exposition.OrthogonalPolynomials