- MathNotebook
- MathConcepts
- StudyMath
- Geometry
- Logic
- Bott periodicity
- CategoryTheory
- FieldWithOneElement
- MathDiscovery
- Math Connections
Epistemology
- m a t h 4 w i s d o m - g m a i l
- +370 607 27 665
- My work is in the Public Domain for all to share freely.
- 读物 书 影片 维基百科
Introduction E9F5FC
Questions FFFFC0
Software
Adjunction, Equivalence, Sameness, Definition of adjunction, Category theory, Limits vs colimits, Six functor formalism
Classify the kinds of adjoint strings
Exposition.ClassifyingAdjunctionsVon Neumann's unitary operator (which takes lines to lines) is like Plato's "unlimited" (as with cold or hot). Think also about the "limited".
Kress, Gunther R.; Van Leeuwen, Theo (2006). Reading Images: The Grammar of Visual Design. New York: Routledge. ISBN 0-415-31915-3.
Classify examples of equivalences.
- Collect examples of equivalences, especially those which are not isomorphisms.
- Understand isomorphism and equivalence as adjunctions.
- Relate the kinds of equivalences to the kinds of adjunctions.
Classify adjoint strings.
- Study examples to understand how adjoint functors deviate from equivalences, deviate from being full and/or faithful, thus whether the induced homset functions are surjective and injective.
- Identify and classify trivial functors.
- Focus on what the functor does to the morphisms. For example, a set function becomes a group homomorphism, and a group homomorphism becomes a set function. An inequality amongst the reals becomes an inequality amongst the integers, and vice versa.
- Understand the reasons why or why not a left or right adjoint functor exists.
- Study and classify adjunction explosions (going back and forth) to show how a function, a flow of implications of a stance is set up. It is a logical swirl, a logical spiral.
- Wenbo raises the question about adjunctions, at what point in the chain of composition do we get identity. For example, is GF(A) = GFGF(A)?
Understand the classification
- Understand how adjoint strings carve out contexts.
- Understand how they manifest that information stays the same but context changes.
- In what sense does the classification of adjunctions show the relation between category (limits, colimits) and logic (universal, existential) and programming (tensor, hom) and the Curry-Howard-Lambek trinity?
Classify the kinds of trivial functors.
- Why and how do adjoint functors arise from trivial functors?
- Adjunctions are with regard to various "do nothing" functors. Catalogue the possibilities.
- Linearity, multilinearity, tensors, etc. are triviality - how does that relate to adjunctions?
- What is the difference between trivial actions (defined by adjunctions) and the null action (defined by the Yoneda lemma)?
- Think of the kinds of triviality as the ways of the abuses of notation.
Classify the kinds of paradigmatic, illustrative examples.
- Adjunctions should relate to developing a theory of most illustrative examples. Develop such a theory of examples for category theory. Perhaps there may be several examples needed in more sophisticated cases. The set of examples would relate to the perspectives in the corresponding division of everything.
Self-adjoint operators
- Are 3x3 matrices of octonions self-adjoint?
Free and forgetful
- Do free and forgetful functors relate a category with its subcategory?
- What exactly is the distinction between including and forgetting?
- What would be the adjoint functors to various forgettings in analysis such as going from Euclidean space to a metric space (retaining simply the distance metric). When does the adjoint functor exist?
- Why, for topologies, do we have indiscrete {$\vdash$} forgetful {$\vdash$} discrete, whereas for categories it is the other way around discrete {$\vdash$} forgetful {$\vdash$} indiscrete ?
- How does the Varela adjunction (building a tree, pointed graph) relate to walks on trees?
Syntax-semantics adjunction
- If a functor takes us from a syntactic category to a semantic category, then what does the adjoint functor mean?
Diagonal functor
- In what sense can every adjunction be thought of, by way of the adjoint functor theorems, as involving a diagonal functor?
- How do the 6 ways of proof relate to the classification of adjunctions? For example, they both include substitution.
Tensor product - Homset
- Where are tensor products used in free constructions, the left adjoints of forgetful functors? And how does that relate to the tensor product - homset adjunction?
- Is the isomorphism of a vector space with its double dual an example of the tensor product - homset adjunction?
- How could we introduce another category and a forgetful functor in between the reduced suspension and loopspace functors? (perhaps by looking at topological spaces without a base point.)
- In what sense do functors between G-Set and Set encompass the various adjunctions through an intermediate functor? (For example, the constant functor from Set to G-Set has left-adjoint all and right-adjoint exists, and the forgetful functor from G-Set to Set has left-adjoint tensor and right-adjoint hom.)
- In the case of preorders, show whether Meet : XxX to X has a right adjoint.
- What is the Tensor-Hom relationship in Hopf algebras? and how is that expressed by the symmetric functions? and how does that express the twosome?
- If the twosome grounds parallel vs. series, does the threesome relate them with sequence, hierarchy, network? and how?
- How is the Jacobi identity related to the Tensor-Hom adjunction? They both involve [X,[Y,Z]]. And how does that relate to the adjoint operator for a Lie algebra?
- HomSet and Tensor express perfect duality between external and internal. Which is which?
- Understand tensors in terms of Penrose graphical notation. What would be homsets?
- Twosome is given by two of Grothendieck's six operations: Tensor and Hom. So understand which is opposites coexisting and which is all the same. And they are related to the triplets of dualities, internal and external, so pursue that connection.
Image functors
- Study the etale cohomology to understand an example of the six functor formalism.
- Study the examples of derived functors and consider how that illustrates the six functor formalism.
- What happens to the sheaf functors if for {$f:X\rightarrow Y$} we have {$X=Y$}? and thus {$\textrm{Sh}(X)=\textrm{Sh}(Y)$}?
- How to make sense of the exceptional inverse image functor {$f^!$} or {$Rf^!$}. And to understand
 derived functors and how they continue a short exact sequence with a long exact sequence. And so also learn about Verdier duality, derived category, Abelian category and snake lemma.
derived functors and how they continue a short exact sequence with a long exact sequence. And so also learn about Verdier duality, derived category, Abelian category and snake lemma.
- Can the left-right order of the direct image functor - inverse image functor adjunction be changed simply by changing {$\subset$} to {$\supset$} ?
- Find a combinatorial expression of the Grothendieck yoga, for example, considering how sets are partitioned. Or the combinatorics of Hopf algebras, of symmetric functions.
- Is the fivesome an adjoint quadruple as with cohesive topos?
- What is more basic, Set or Pointed set?
Quantifiers
- What is the cognitive basis for the adjoint string Existential quantifier {$\dashv$} Constant function {$\dashv$} Universal quantifier ?
- What is the significance for classifying adjunctions that {$X\rightarrow 2$} is a map whereas {$J\rightarrow C$} is a functor? Or are they both functors?
- Can all logical connectives be thought of as adjoint functors, as with "for all" and "there exists"?
- How does the arithmetic hierarchy express Human's view (there exists) of God's view (for all)? What does it mean to negate? Relate to adjoint strings, duality by negation, as with floor-inclusion-ceiling.
- Consider the relation between adjunctions, lenses, databases.
- Study existential and universal quantifiers as adjunctions and as the basis for the arithmetical hierarchy.
- "For all" and "there exists" are adjoints presumably because they are on opposite sides of a negation wall that distinguishes the internal structure and external relationships. (That wall also distinguishes external context and internal structure.) (And algorithms?) So study that wall, for example, with regard to recursion theory.
What is an intuitive view of adjoints? (version 1: category theory) Come up with my best answer!
- Understand the tensor product.
- Understand how adjunctions differ with regard to monads, fullness and faithfulness
- Understand Kleisli and Eilenberg-Moore monads.
读物
Examples of adjunctions
- Saunders MacLane. Categories for the Working Mathematician. IV.Adjoints. Contains many examples and a taxonomy of sorts.
- nLab: Adjoint modality - similar to my efforts to classify
- StackExchange: A Bestiary about Adjunctions
- StackExchange: Some beautiful examples of adjunctions including inclusion of Z and R, with floor and ceiling as adjunct functors on either side
- StackExchange: If adjunction arises everywhere, where is it in the fundamental theorem?
- 维基百科: List of adjoint functors
Helpful ideas about adjunctions
- Math Stack Exchange: How is the notion of adjunction of two functors usefull?
- Matías Menni, Clara Smith. Modes of Adjointness Traces the concept of adjunction back to the origins of the algebraic semantics of modal logic and makes explicit its ubiquity in this branch of mathematics.
- Makkai and Reyes start by stating that categorical logic rests on Lawvere’s insight that fundamental logical operations arise as adjoints to naturally given functors
Existence of left or right adjoint functors
- Formal criteria for adjoint functors - Freyd and Kan
- Math Overflow. How do I check if a functor has a (left/right) adjoint?
Examples of left adjoints and right adjoints
| Name | Categories and Functors | Hom-Set adjunction | Bijection |
| Tensor product - HomSet | {$ \_ \otimes_R Y : \textrm{Mod}_R\leftrightarrow$}{$\textrm{Mod}_S : \textrm{Hom}_S(Y,\_)$} | {$\textrm{Hom}(X\otimes Y,Z)\cong$}{$\textrm{Hom}(X,\textrm{Hom}(Y,Z))$} | {$[f(x\otimes y)=z] \leftrightarrow$}{$ [\bar{f}(x)(y)=z]$} |
| Induction restriction | {$\textrm{Ind}^G_H : \textrm{Rep}_H \leftrightarrow$}{$ \textrm{Rep}_G : \textrm{Res}^G_H $} | {$\textrm{Hom}(\textrm{Ind}^G_H(\rho_W),\theta_V)\cong$}{$\textrm{Hom}(\rho_W,\textrm{Res}^G_H(\theta_V))$} | {$\Phi\leftrightarrow$}{$\Phi\circ i^G_H$} |
| Direct image - Inverse image for {$f:A\rightarrow B$} | {$f_*:PA\leftrightarrow $}{$ PB:f^{-1}$} | {$\textrm{Hom}_{PB}(f_*(A'),B')\cong$}{$\textrm{Hom}_{PA}(A',f^{-1}(B'))$} | {$f_*(A')\leq B'\Leftrightarrow $}{$ A'\leq f^{-1}(B')$} |
| Inverse image - Proper image for {$f:A\rightarrow B$} | {$f^{-1}:PB\leftrightarrow $}{$ PA:f_!$} | {$\textrm{Hom}_{PA}(f^{-1}(B'),A')\cong$}{$\textrm{Hom}_{PB}(B',f_!(A'))$} | {$f^{-1}(B')\leq A'\Leftrightarrow $}{$B'\leq f_!(A')$} |
Overview
Adjunctions express the possible relationship between two categories. This is the basis for classification of adjunctions.
- Seems related to the sevensome of dualities (of opposites).
- Give the ways of expanding a category. Consider maps into it, or select within it a subcategory, or substitute it into a diagram. And also can relate the maps and the diagram. And this may relate to the three-cycle in the house of knowledge - extending a domain (forgetful functor), critical points and continuity (constant functor), superposition of a sequence (diagonal functor). And it may relate to levels of consciousness, to levels of understanding. But what does that have to do with divisions of everything?
- Note the direction that the trivial functors take us. The forgetful functor takes us from D to C, and then the constant function functor takes us further from C to {$C^X$}, and substitution takes us from C to {$C^J$}.
- Identity functor
- Isomorphism
- Equivalence.
- The unit is a natural isomorphism from {$FG$} to {$I_D$} and likewise the counit is a natural isomorphism from {$GF$} to {$I_C$}. Alternatively, {$F\dashv G$} where both functors are full and faithful.
- Also: Self-adjointness
- Duality.
- Equivalence in opposite directions.
- Compatible adjoint functors
- When the two categories are the same, we can include an intermediate inclusion functor.
- Greatest lower bound and least upper bound. Galois connection.
- Efficient solution vs. Difficult problem
- Minimal axiomatization (smallest set of keys to open a set of locks) left adjoint to Totality of satisfaction (maximum set of locks that can be opened by a set of keys)
- Insert category into diagram.
- Left adjoint is colimit of diagram. Right adjoint is limit of diagram. (This grounds my intuition about internal structure and external relationships.)
- Categories must be different. One is more selective, thus has more structure than the other. Ignoring algebraic structure given by operations.
- Free construction is left adjoint to Forgetful functor.
- Left adjoint to free construction is the enveloping functor.
- Right adjoint to Forgetful functor is the minimal construction for definition of added structure (left adjoint is maximal construction)
- Tensor - forgetful - hom (when we are working with a single ring R and forgetting takes R-modules to abelian groups)
- Inclusion of Z into R, free = least upper bound, cofree = greatest lower bound.
- Categories may or may not be different: R-modules vs. S-modules
- Tensor product (internal structure) is left adjoint to Hom functor (external relations).
- Vector space mapped to dual vector space and back. (This is a trivial case of tensor product - homset where y=Id.)
- Category C and {$C^X$}. Defining a constant function.
- Left adjoint is "there exists" value, right adjoint is "for all" value.
- Ignoring topological structure given by grouping. Discrete topology is left adjoint to this, and indiscrete topology is right adjoint to this.
- Aggregation of elements. (Can and should switch order to make compatible.) Left adjoint of inverse image functor is direct image functor, and right adjoint of inverse image functor is the proper image functor. And the right adjoint functor of the proper image functor leads to the infinite three-cycle.
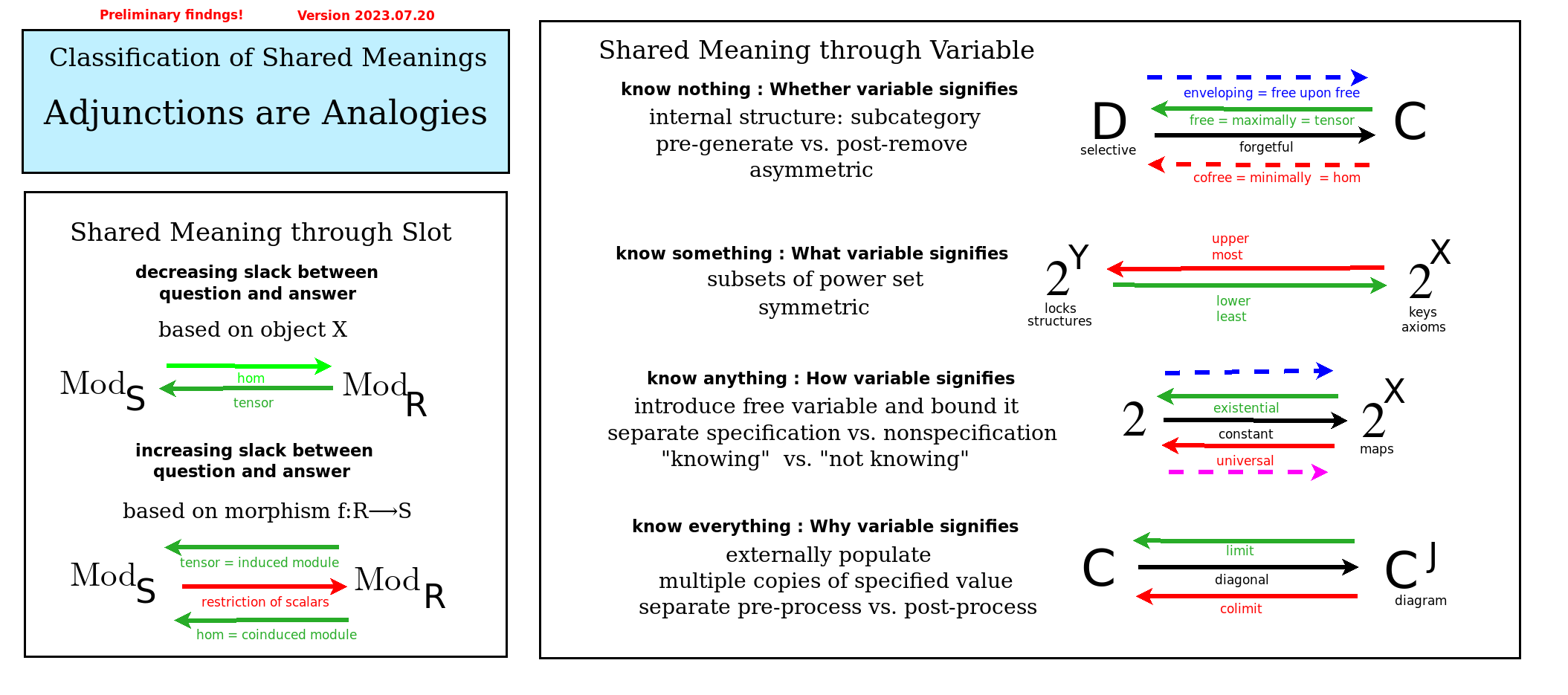
Classification of adjunctions
- The classification establishes 8 categories arranged in 2 sets of 4.
- One set is the perspective formula that relates {$D$}, {$C$}, {$C^X$}, {$C^J$}. It describes the relation between inner structure and external relationships both internally (in terms of {$D$} and {$C$}) and externally (in terms of {$C^X$} and {$C^J$}.
- The other set is a pair of axes ({$2^X$} and {$2^Y$}) and ({$\textrm{Mod}_S$} and {$\textrm{Mod}_R$}) that ground the foursome. They add structure and distinction to the categories.
- The diagonal functor grounds an adjoint triple (nonextendible?). The constant functor grounds an adjoint septuplet (at most). Together they express how the three-cycle works together with the divisions of everything (up to the sevensome) to create structure (as in the house of knowledge).
- The free and forgetful functors ground a fourfold adjoint string (maximally?) which may express the foursome.
- John Baez. Total Freedom. Six kinds of free and forgetful adjoints?
Ideas
General principle: left adjoint is local, right adjoint is global.
Classification of adjoint strings expresses the possiblities for harmonization of the semantics of information (which stays the same) and the syntax of context (which changes). Thus adjoint strings express the ways that a division into information and context can be understood within the context of divisions of everything, namely, within the context of the eightsome. Consider the adjoint string with seven functors, and the infinite adjoint string with period six.
Different kinds of adjunctions are different kinds of equivalences (or wholeness preserving transformations) such as freely generating or forgetting structure, inclusion and restriction - extending or restricting the domain, making copies or eliminating them.
The identity functor can be thought of as the trivial functor for adjunctions involving dualities, two compatible functors.
Isomorphisms
Two categories C and D are isomorphic if there exist functors {$F:C\to D$} and {$G:D\to C$} which are mutually inverse to each other, that is, {$FG=1_{D}$} (the identity functor on D) and {$ GF=1_{C}$} (the identity functor on C).
| identity functor {$\textrm{id}_\textbf{C}:\textbf{C}\rightarrow\textbf{C}$} | identity functor {$\textrm{id}_\textbf{C}:\textbf{C}\rightarrow\textbf{C}$} |
Self-adjoint functor
Galois connections that are isomorphisms
Galois connection Let G act transitively on X (so that for each pair x, y in X there exists a g in G such that {$g\cdot x = y$}). And pick some point x in X. Consider {$\mathcal{B} = \{B \subseteq X : x \in B; \forall g \in G, gB = B \ \mathrm{or} \ gB \cap B = \emptyset\},$} the set of blocks containing x. Further, let {$\mathcal{G}$} consist of the subgroups of G containing the stabilizer of x. ({$G_x = \{g\in G | g\cdot x = x\}$}). Then, the correspondence {$\mathcal{B} \to \mathcal{G}$} where {$B \mapsto H_B = \{g \in G : gx \in B\}$} is a monotone, one-to-one Galois connection (because the action is transitive). (I think this is an isomorphism.)
Equivalences
An equivalence is a translation. A translation is sucessful if the corresponding terms (the translated term and the compared term) have analogous structure and if the terms are explicitly connected. If the terms are different in structure or if they have no connecting link then the translation is not achieved.
An equivalence can be defined as follows:
- An equivalence is a pair of functors {$F$}, {$G$} with natural isomorphisms {$\eta:\textbf{1}_\textbf{C}\rightarrow {G∘F}$}, {$\epsilon:F∘G\rightarrow {1}_\textbf{D}$}. The natural isomorphisms {$\eta_{C} \eta^{-1}_{C}={1}_{G∘F(C)}$}, {$\eta^{-1}_{C} \eta_C ={1}_{C}$}, {$\epsilon_{D} \epsilon^{-1}_{D}={1}_{D}$}, {$\epsilon^{-1}_{D}\epsilon_{D}={1}_{F∘G(D)}$}.
- This is similar to the definition of adjunction in terms of unit and counit.
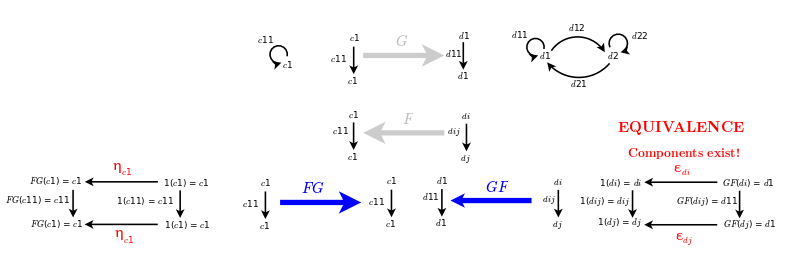
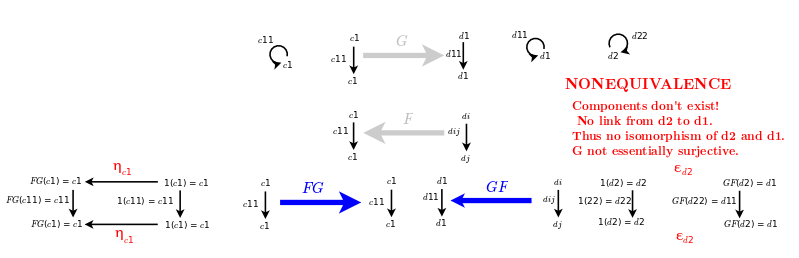
- A functor is an equivalence if and only if it is full, faithful and essentially surjective on objects.
- A functor is full if the function {$\textbf{C}(C,C')\rightarrow \textbf{D}(F(C),F(C'))$} is surjective for all {$C$}, {$C'$} in {$\textbf{C}$}.
- A functor is faithful if the function {$\textbf{C}(C,C')\rightarrow \textbf{D}(F(C),F(C'))$} is injective for all {$C$}, {$C'$} in {$\textbf{C}$}.
- A functor is essentially surjective on objects if for all {$D\in \textbf{D}$}, there exists {$C\in\textbf{C}$} such that {$F(C)\cong D$}.
- This is similar to the definition of adjunction in terms of homsets, and also in terms of the universal mapping property.
If F : D → C is an equivalence of categories, then we have an inverse equivalence G : C → D, and the two functors F and G form an adjoint pair. The unit and counit are natural isomorphisms in this case. Examples
See:  Equivalence of categories: Examples
Equivalence of categories: Examples
- Leinster 36. "let A be the category whose objects are groups and whose maps are all functions between them, not necessarily homomorphisms. Let {$Set_{\neq ∅}$} be the category of nonempty sets. The forgetful functor U : A → {$Set_{\neq ∅}$} is full and faithful. It is a (not profound) fact that every nonempty set can be given at least one group structure, so U is essentially surjective on objects. Hence U is an equivalence. This implies that the category A , although defined in terms of groups, is really just the category of nonempty sets. Andrius: This example shows that the faithfulness and fullness are with regard to the homsets, not the objects. Thus we may have two different groups on the same elements and which thus get mapped to the same set but their homsets remain in bijection between the category of groups and the category of nonempty sets.
- Wikipedia: Consider the category {$C$} having a single object {$c$} and a single morphism {$1_{c}$}, and the category {$D$} with two objects {$d_{1}$}, {$d_{2}$} and four morphisms: two identity morphisms {$1_{d_{1}}$}, {$1_{d_{2}}$} and two isomorphisms {$\alpha \colon d_{1} \to d_{2}$} and {$\beta \colon d_{2} \to d_{1}$}. The categories {$C$} and {$D$} are equivalent; we can (for example) have {$F$} map {$c$} to {$d_{1}$} and {$G$} map both objects of {$D$} to {$c$} and all morphisms to {$1_{c}$}.
- By contrast, the category {$C$} with a single object and a single morphism is not equivalent to the category {$E$} with two objects and only two identity morphisms. The two objects in {$E$} are not isomorphic in that there are no morphisms between them. Thus any functor from {$C$} to {$E$} will not be essentially surjective. This example shows that isomorphism is defined not absolutely as to the form but with regard to the morphisms in the category itself.
- Leinster p.35 Let A be any category, and let B be any full subcategory containing at least one object from each isomorphism class of A . Then the inclusion functor {$B ,→ A$} is faithful (like any inclusion of subcategories), full, and essentially surjective on objects. Hence B is equivalent to A. So if we take a category and remove some (but not all) of the objects in each isomorphism class, the slimmed-down version is equivalent to the original. Conversely, if we take a category and throw in some more objects, [along with the relevant morphisms to and from all isomorphic objects, and other objects], each of them isomorphic to one of the existing objects, it makes no difference: the new, bigger, category is equivalent to the old one.
- Leinster p.35 Let FinSet be the category of finite sets and functions between them. For each natural number n, choose a set n with n elements, and let B be the full subcategory of FinSet with objects 0, 1, . . . . Then B is equivalent to FinSet, even though B is in some sense much smaller than FinSet.
- Leinster p.35 Let C be the full subcategory of CAT whose objects are the one-object categories. Let Mon be the category of monoids. Then C ' Mon. To see this, first note that given any object A of any category, the maps A → A form a monoid under composition (at least, subject to some set-theoretic restrictions). There is, therefore, a canonical functor F : C → Mon sending a one-object category to the monoid of maps from the single object to itself. This functor F is full and faithful (by Example 1.2.7) and essentially surjective on objects. Hence F is an equivalence.
- If f is the inclusion of a closed subspace {$X ⊆ Y$} then the direct image functor {$f_*$} is exact. Actually, in this case {$f_∗$} is an equivalence between sheaves on X and sheaves on Y supported on X. It follows from the fact that the stalk of {$( f_∗ \mathcal{F})_{\mathcal{y}}$} is {$\mathcal{F}_{\mathcal{y}}$} if {$y\in X$} and zero otherwise (here the closedness of X in Y is used).
- “Prove the classical version of Stone’s representation theorem and interpret it in the terms of category theory.” By a famous result of Marshall H. Stone’s, totally disconnected compact Hausdorff spaces, so-called Stone spaces, are dual to Boolean algebras, i.e., the first category is categorically equivalent to the opposite category of the second one. The duality between the two categories is realized by means of a dualizing object, meaning that the equivalence can be expressed as a restriction of a representable functor.
 Equivalence of categories Consider the category {$C$} of finite-dimensional real vector spaces, and the category {$D=\textrm{Mat}(\mathbb{R})$} of all real matrices (the latter category is explained in the article on additive categories). Then {$C$} and {$D$} are equivalent: The functor {$G\colon D\to C$} which maps the object {$A_{n}$} of {$D$} to the vector space {$\mathbb{R}^{n}$} and the matrices in {$D$} to the corresponding linear maps is full, faithful and essentially surjective.
Equivalence of categories Consider the category {$C$} of finite-dimensional real vector spaces, and the category {$D=\textrm{Mat}(\mathbb{R})$} of all real matrices (the latter category is explained in the article on additive categories). Then {$C$} and {$D$} are equivalent: The functor {$G\colon D\to C$} which maps the object {$A_{n}$} of {$D$} to the vector space {$\mathbb{R}^{n}$} and the matrices in {$D$} to the corresponding linear maps is full, faithful and essentially surjective.
Also: Self-Adjoint
The duality involution {$(−)^{op}:\textrm{Cat}\rightarrow\textrm{Cat}$} is self-adjoint.
If a category C has biproducts, then the composite {$⊕∘Δ_n$} of the (discrete n-ary) diagonal functor {$Δ_n$} with the (n-ary) biproduct functor {$⊕$} is self-adjoint.
The contravariant powerset functor {$P:Set→Set^{op}$} is left-adjoint to {$P^{op}:Set^{op}→Set$}, i.e. self-adjoint on the right.
More generally, in a symmetric monoidal closed category {$(C,⊗,I,⊸)$}, for a fixed object A, the functor {$(−)⊸A$} is self-adjoint on the right.
Self-adjoint operator
- Self-adjoint. Algebra = geometry. Local = global. Topological group, Lie group.
- https://encyclopediaofmath.org/wiki/Self-adjoint_differential_equation
- https://encyclopediaofmath.org/wiki/Adjoint_differential_equation
- https://encyclopediaofmath.org/wiki/Adjoint_operator
- Self-adjoint operators are adjunctions in both directions. They are like machines that are symmetrical operating in the forwards and backwards directions. This is physically meaningful for time reversibility.
- Self-adjoint operator may show the equivalent effect (introducing conjugate) of the rotation of a tensor and the rotation of a coordinate space.
- Stone's theorem (the dynamical evolution)
- Spectral theorem (the structure): One-to-one connection between projections (measure valued projections) and self-adjoint operators.
Quantum measurement projects into eigenstate. The projection operator is a mathematical statement of the collapse of the wave function. If you do it twice, then you don't get anything more.
- Self-adjoint operators are weighted sums of projection operators. The weights you can find from experiments by applying a projection operator.
Dualities
Leinster p.35: An equivalence of the form {$A^{op}\simeq B$} is sometimes called a duality between A and B. One says that A is dual to B. There are many famous dualities in which A is a category of algebras and B is a category of spaces.
Leinster: For certain classes of space, the passage from X to C(X) loses no information: there is a way of reconstructing the space X from the ring C(X). For this and related reasons, it is sometimes said that ‘algebra is dual to geometry’. Given a topological space X, let C(X) be the ring of continuous real-valued functions on X. The ring operations are defined ‘pointwise’: for instance, if {$p_1 , p_2 : X → R$} are continuous maps then the map {$p_1 + p_2 : X → R$} is defined by {$(p_1 + p_2 )(x) = p_1 (x) + p_2 (x)(x ∈ X)$}. A continuous map {$f : X → Y$} induces a ring homomorphism {$C( f ) : C(Y) → C(X)$}, defined at {$q ∈ C(Y)$} by taking {$(C( f ))(q)$} to be the composite map {X \overset{f}{\rightarrow} Y \overset{q}{\rightarrow} R.$} Note that {$C( f )$} goes in the opposite direction from f . After checking some axioms (Exercise 1.2.26), we conclude that C is a contravariant functor from Top to Ring.
- Stone duality: the category of Boolean algebras is dual to the category of totally disconnected compact Hausdorff spaces.
- Gelfand–Naimark duality: the category of commutative unital C ∗ -algebras is dual to the category of compact Hausdorff spaces. (C ∗ -algebras are certain algebraic structures important in functional analysis.)
- Algebraic geometers have several notions of ‘space’, one of which is ‘affine variety’. Let k be an algebraically closed field. Then the category of affine varieties over k is dual to the category of finitely generated k-algebras with no nontrivial nilpotents.
- Pontryagin duality: the category of locally compact abelian topological groups is dual to itself. As the words ‘topological group’ suggest, both sides of the duality are algebraic and geometric. Pontryagin duality is an abstraction of the properties of the Fourier transform.
- Let V be a vector space with inner product. Given subspace X of V, consider the orthogonal complement F(X). The functor F is its own left and right adjoint. It describes an antitone Galois connection.
- If topological space X is path-connected, locally path-connected and semi-locally simply connected, then there is a bijection between equivalence classes of path-connected covers of X and the conjugacy classes of subgroups of the fundamental group {$\pi_1(X, x)$}. This is an antitone Galois connection.
 Covering spaces
Covering spaces
Isbell duality. Preorders.
{$(𝒪⊣Spec):CoPresheaves\overset{𝒪}{\underset{Spec}{⇆}}Presheaves$}
Spec is the left Kan extension of the Yoneda embedding along the contravariant Yoneda embedding, while 𝒪 is the left Kan extension of the contravariant Yoneda embedding along the Yoneda embedding.
In the simplest case, namely for an ordinary category {$\mathcal{C}$}, the adjunction between presheaves and copresheaves arises as follows...
- The presheaf category {$[\mathcal{C}^{op}, \mathrm{Set}]$} has all limits, so we can extend the Yoneda embedding to a continuous functor
{$Y \colon [\mathcal{C}, \mathrm{Set}]^{op} \to [\mathcal{C}^{op}, \mathrm{Set}]$} from copresheaves to presheaves.
- Dually, the copresheaf category {$[\mathcal{C}, \mathrm{Set}]^{op}$} has all colimits, so we can extend the co-Yoneda embedding to a cocontinuous functor {$Z \colon [\mathcal{C}^{op}, \mathrm{Set}] \to [\mathcal{C}, \mathrm{Set}]^{op}$} from presheaves to copresheaves.
- Isbell duality says that these are adjoint functors: Y is right adjoint to Z.
The more general case deals with enrichment.
nLab: Spec is the left Kan extension of the Yoneda embedding along the contravariant Yoneda embedding, while {$\mathcal{O}$} is the left Kan extension of the contravariant Yoneda embedding along the Yoneda embedding.
nLab: The codensity monad of the Yoneda embedding is isomorphic to the monad induced by the Isbell adjunction, {$Spec \mathcal{O}$} (Di Liberti 19, Thrm 2.7).
Geometry and algebra as duals by way of adjunctions
- “Make the popular heuristic that geometry and algebra are two sides of the same coin precise in the framework of category theory!” Following William T. Lawvere, (generalized) spaces can be formalized as presheaves and (generalized) algebras of functions over a space as co-presheaves. In the special case of enriched (co-)presheaves the left Kan extensions of the covariant and contravariant enriched Yoneda-embeddings along each other then define an enriched adjunction between spaces and function algebras, the Isbell conjugacy. More generally, the theory of the Isbell envelope allows reasoning about whether two categories satisfy such a notion of Isbell duality. Knowledge of topic no. 4 has to be considered a prerequisite. Though not strictly necessary, understanding a bit of topic no. 16 will be helpful. [Isb66]
nLab: duality between algebra and geometry
- nLab: The duality relevant to the spectral theory is the duality commutative von Neumann algebras and compact strictly localizable enhanced measurable spaces.
 Equivalence of categories One of the central themes of algebraic geometry is the duality of the category of affine schemes and the category of commutative rings. The functor G {\displaystyle G} G associates to every commutative ring its spectrum, the scheme defined by the prime ideals of the ring. Its adjoint F {\displaystyle F} F associates to every affine scheme its ring of global sections.
Equivalence of categories One of the central themes of algebraic geometry is the duality of the category of affine schemes and the category of commutative rings. The functor G {\displaystyle G} G associates to every commutative ring its spectrum, the scheme defined by the prime ideals of the ring. Its adjoint F {\displaystyle F} F associates to every affine scheme its ring of global sections.Dualizing object
- nLab: Dualizing object homming into an object induces dual adjunctions
Fausk, Hu, May: There are many contexts in algebraic geometry, algebraic topology, and homological algebra where one encounters a functor that has both a left and right adjoint, with the right adjoint being isomorphic to a shift of the left adjoint specified by an appropriate "dualizing object". Typically the left adjoint is well understood while the right adjoint is more mysterious, and the result identifies the right adjoint in familiar terms.
Adjoint equivalences
nLab: Adjoint equivalence An adjoint equivalence between categories is an adjunction {$f\dashv g$} in which the unit {$\eta$} and counit {$\varepsilon$} are natural isomorphisms.
Somewhat related? Ambidextrous adjunction. An adjoint triple {$F \dashv G \dashv H$} is called an ambidextrous adjunction (or sometimes ambijunction, for short) if the left adjoint F and the right adjoint H of G are equivalent {$F \simeq H$}.
- nLab: Fundamental theorem of covering spaces For a sufficiently well-behaved topological space X, the functor which sends a covering space of X to the Set-action (permutation representation) of the fundamental groupoid of X on the fibers of E is an equivalence of categories.
- nLab By the universal property of 1-truncation we have an equivalence: {$(‖X‖ 1→Sets)≃(X→Sets)$}
- nLab: Grothendieck's Galois theory Let X be a connected scheme. Then there exists a profinite group {$\pi_1(X)$} – the fundamental group of X – uniquely determined up to isomorphism, such that the category of finite étale coverings {$FEex$} is equivalent to the category {$Fin \pi_1(X) Set$} of finite permutation representations of {$\pi_1(X)$} (finite sets, with the discrete topology, on which {$\pi_1(X)$} acts continuously).
- Grothendieck construction establishes equivalences of bicategories, {$Fib(C)≃2Func(C^{op},Cat)$} and {$Fib_{Grpd(C)}≃2Func(C^{op},Grpd)$}
Compatible functors. Galois connections.
Preorders. Greatest lower bound and least upper bound. Galois connection.
Lower (left) adjoint vs. Upper (right) adjoint
- Let (A, ≤) and (B, ≤) be two preorders (such as partially ordered sets or equivalences). A monotone Galois connection between these posets consists of two monotone functions: F : A → B and G : B → A, such that for all a in A and b in B, we have {$Fa≤b\Leftrightarrow a≤Gb$}.
For categories arising from partially ordered sets {$(P,\leq )$} (with a single morphism from {$x$} to {$y$} if and only if {$x\leq y$}), then adjoint pairs are Galois connections and monads are closure operators.
 Galois connection An essential property of a Galois connection is that an upper/lower adjoint of a Galois connection uniquely determines the other:
Galois connection An essential property of a Galois connection is that an upper/lower adjoint of a Galois connection uniquely determines the other:- F(a) is the least element ~b with a ≤ G(~b), and
- G(b) is the largest element ~a with F(~a) ≤ b.
A consequence of this is that if F or G is invertible, then each is the inverse of the other, i.e. {$F = G^{-1}$}.
| Lower (left) adjoint | Upper (right) adjoint | Notes |
| Inclusion Inc of open subset {$U$} as a subset | Interior Int of a set {$A$} is the union of open sets inside of {$A$} | Awodey 9.11. Inclusion: Open Sets {$\mathcal{O}(X)$} into Power Set {$\mathcal{P}(X)$} and Interior yield a bicondition: {$\mathbf{inc}(U)\subseteq A \Leftrightarrow U\subseteq\mathbf{int}(A)$} |
| Exterior Ext of a set {$A$} is the intersection of closed sets containing {$A$} | Inclusion Inc of closed subset {$U$} as a subset | Awodey 9.11. Inclusion: Open Sets {$\mathcal{O}(X)$} into Power Set {$\mathcal{P}(X)$} and Exterior yield a bicondition: {$U\subseteq\mathbf{ext}(A)\Leftrightarrow \mathbf{inc}(A)\subseteq U $} |
| Sup(L) gives supremum of downset lattice | Embed(x) maps poset element x to principal ideal D(x) = {$\{y\in X|y\leq x\}$} | Embed: Poset X {$\leftrightarrow$} D(X): Sup  Completeness in terms of adjunctions Does Embed have right adjoint? Compare with inclusion of Z into R. Completeness in terms of adjunctions Does Embed have right adjoint? Compare with inclusion of Z into R. |
Seven sketches 1.71. Consider the map {$(3 × −) : \mathbb{N}\rightarrow\mathbb{R}$} which sends x ∈ N to {$3x\in\mathbb{R}$} . Consider the functions {$\lceil x/3 \rceil :\mathbb{R}\rightarrow\mathbb{Z}$} and {$\lfloor x/3 \rfloor :\mathbb{R}\rightarrow\mathbb{Z}$}
- {$x ≤ 3y$} if and only if {$\lceil x/3 \rceil ≤ y $}. Thus {$3 × −$} is right adjoint to {$\lfloor −/3 \rfloor$}.
- {$3x ≤ y$} if and only if {$x ≤ \lfloor y/3 \rfloor$}. Thus {$\lfloor −/3 \rfloor$} is right adjoint to {$3 × −$}.
An antitone Galois connection between A and B is just a monotone Galois connection between A and the order dual {$B^{op}$} of B.
- the connection between fields and groups in Galois theory
- E ↦ Gal(L/E) and G ↦ Fix(G) where subfield E is sent to the group of field automorphisms of L that hold E fixed, and subgroup G is sent to the field consisting of all elements of L that are held fixed by all elements of G. A is the set of all subfields of L that contain K, ordered by inclusion. B is the set of subgroups of Gal(L/K), ordered by inclusion.
- the connection between subsets of vector space V and V*, where V is a vector space with inner product. This expresses orthogonality.
- Given subset of V, define annihilator F(X) as the set of elements of V* that vanish on X. Given subset Y of V*, define G(Y) as the maximal subset of V on which the elements of Y all vanish
- the connection between polynomials and their roots in algebraic geometry
- The variety of zeros (the set of common zeros of the polynomials in S) {$V(S):2^{K[X_1,...,X_n]}\rightarrow 2^{K^n}$} is defined by {$V(S)=\{x\in K^n : f(x)=0 \textrm{for all} f\in S\}$}. The ideal of polynomials vanishing on U is {$I(U): 2^{K^n}\rightarrow 2^{K[X_1,...,X_n]}$} defined as {$I(U) = \{f \in K[X_1,\dots,X_n] : f(x) = 0 \mbox{ for all } x \in U\}$}.
- given a commutative ring R (not necessarily a polynomial ring), there is an antitone Galois connection between radical ideals in the ring and subvarieties of the affine variety Spec(R).
- there is an antitone Galois connection between ideals in the ring and subschemes of the corresponding affine variety.
Is this a Galois connection? The ideal quotient is adjoint to the multiplication by ring ideals.
- If I and J are ideals of a commutative ring R, their ideal quotient (I : J) is the set {$(I:J)=\{r\in R\mid rJ\subseteq I\}$}, which itself is an ideal in R.
- Division is (in general) the attempt to invert multiplication, but in situations where this is not possible, we often attempt to construct an adjoint instead.
Any relation R on X×Y defines a Galois connection.
A function f is a lower (resp. upper) adjoint if and only if f is a residuated mapping (resp. residual mapping). If A, B are posets, a function f: A → B is residuated if and only if the preimage under f of every principal down-set of B is a principal down-set of A. A principal down-set to be one of the form ↓{b} = { b' ∈ B : b' ≤ b }.
Marcel Erné. Adjunctions and Galois Connections: Origins, History and Development.
- the theory of polynomial equations (Lagrange, Galois),
- the modern Galois theory (Dedekind, Artin),
- the origins of lattice theory (Dedekind, Schröder),
- the polarities and lattice-theoretical aspects (Birkhoff),
- the order-theoretical Galois connections (Ore),
- the logical calculus (Boole, Peirce, Schröder),
- the residuation theory (Krull, Ward, Dilworth)
Tai Danae Bradley: Formal Concept Analysis, Simon Willerton: Formal Concept Analysis
- {$B\subseteq fA$} (each feature in B is possessed by every element in A) iff {$A\subseteq gB$} (each element in A has all the features in B).
Efficient solution (minimial axiomatization) vs. Difficult problem (maximal application)
| Left (lower) adjoint | Right (upper) adjoint | Notes |
| give the most efficient solution to the problem posed | pose the most difficult problem that the solution solves | See: Adjoint Functors: Introduction and Motivation |
| "what objects have to exist, and what relations have to exist between them" | "what data can you extract and what restrictions are there on that data" | Comment by Daniel Schepler |
| "syntax functor" F(S) is the minimal axiomatization (optimal syntactic theory) of S | "semantics functor" G(T) is the largest set of all structures (semantic models, algebras) that satisfy the axioms of a theory T. | Lawvere (1969). C is the set of all logical theories (axiomatizations), D is the power set of the set of all mathematical structures, S is a subset of F(T) if and only if G(S) logically implies T |
| minKeys() gives the smallest set of keys to open a set of locks | maxLocks() gives the maximum set of locks that can be opened by a set of keys | Open the most Locks with the least Keys. Runar Bjarnason "Adjunctions in Everyday Life" |
| {$i: P → G$} sends each population to itself as a gene pool {$i(p)=p$} | {$cl: G → P$} sends each gene pool to its closure: the set of all possible animals that could be generated from g under recombination of genes | {$i(p) ≤ g \Leftrightarrow p ≤ cl(g)$} Preorder {$(P, ⊆)$} of possible animal populations, {$p ⊆ q$} if every animal in p is also in q. Preorder (G, ≤) of gene pools, {$1 ≤ h$} if every animal in g could be generated by mating animals in h. Seven sketches 1.74. |
| multiplication by integer y | division by integer y | x,y, z,: BigInt (when y >0); (z * y <= x) == (z <= x / y); (f(z) <= x) == (z <= g(x)) |
An adjunction between categories C and D gives rise to a family of universal morphisms, one for each object in C and one for each object in D. Conversely, if there exists a universal morphism to a functor G : C → D from every object of D, then G has a left adjoint. However, universal constructions are more general than adjoint functors: a universal construction is like an optimization problem; it gives rise to an adjoint pair if and only if this problem has a solution for every object of D (equivalently, every object of C).
- Minimum axioms - remove unnecessary structure - have more examples
- Maximum set of functions - apply to all of space - gives more examples
Passing from adjunctions to monads and back to their monadic adjunctions constitutes itself an adjunction between adjunctions and monads, called the semantics-structure adjunction. (nLab, monad)
- For a category C there exist contravariant functors {$\textrm{Str}:\textrm{Cat}^∗_{/C}\rightarrow \textrm{Mon}(C):\textrm{Sem} with {$\textrm{Str}\dashv\textrm{Sem}$} where {$\textrm{Cat}^∗_{/C}$} denotes the full subcategory of {$\textrm{Cat}_{/C}$} consisting of functors admitting a codensity monad; Str sends a functor to its corresponding codensity monad and Sem sends a monad to the forgetful functor from its E-M category to C. Intuitively speaking we may think of a monad as a kind of structure with which the objects of C can be equipped presented in a syntax-independent way, and we may think of the E-M category of a monad (viewed as a syntax independent presentation of an equational theory) as the category of models of this theory, which is often referred to by logicians as the semantics of the theory.
Possibilities vs. Generator
| Left adjoint | Right adjoint | Notes |
| Assigns to each behavior its free realization. | {$E:Mach(X)\rightarrow Beh(X)$} assigns to each machine its behavior. | Given category {$K$}, input process {$X:K\rightarrow K$}, category of machines {$Mach(X)$}, category of behaviors {$Beh(X)$} Nerode. Universal Realization. |
| functor from reachable automata to behaviors | functor which gives the minimal realization of a behavior | |
| minimal realization | behavior | Goguen 1971 per Maclane's book page 89 |
- Francisco Varela. Principles of Biological Autonomy. Part 1
- Articles about adjunction that cite Varela's "Principles of Biological Autonomy"
- World Cat: Francisco Varela. Principles of Biological Autonomy
Goguen adjunction
- "Realization is Universal"
- Category of machines.
- Objects are sixtuples. Three sets: inputs, outputs, states. Three morphisms: (no-ary) pick an initial state, (unary) state -> output, (binary) input X state -> state. In the case of a Turing machine, the state is the content of the whole tape, and the morphism changes the content of the whole tape.
- Morphisms are machine homomorphisms mapping inputs to inputs, outputs to outputs, states to states.
- Category of behaviors.
- The running of the machines. Can have different implementations of the same behavior.
- Adjunction sends machine to all of its behaviors, and a behavior to a simplest machine that would produce it.
Varela and Goguen
Ideas
- Distinguishing a system with regard to itself and with regard to its environment.
- Establishing system boundaries - cognitive point of view - establishing scope - depends on the cognitive capacities of the distinctor.
- Controlled: Observer may focus on the environment, considering the system as a simple entity with given properties, seeking the regularities of its interaction with the environment.
- Autonomous: Observer may focus on the internal structure of the system, with the properties emerging from the interactions of the component, and the environment simply providing perturbations.
Constant function. Existential and universal quantifiers.
Awodey 9.5. Given distinct variables {$\bar{x}=x_1,x_2,\cdots,x_n$}, define the set of formulas {$\textrm{Form}(\bar{x})=\{\phi(\bar{x})|\phi(\bar{x})$} has at most {$\bar{x}$} free {$\}$}. Define the functor {$*:\textrm{Form}(\bar{x})\rightarrow\textrm{Form}(\bar{x},y)$} which adds a new free variable {$y$}. Then the right adjoint is {$\forall y:\textrm{Form}(\bar{x},y)\rightarrow\textrm{Form}(\bar{x})$} given by {$\forall y.\psi(\bar{x},y)$}. And the left adjoint is {$\exists y:\textrm{Form}(\bar{x},y)\rightarrow\textrm{Form}(\bar{x})$} given by {$\exists y.\psi(\bar{x},y)$}.
Preorders. Defining a constant function
There is a trivial functor that takes us from a constant to a function with that constant value. The left functor will be "there exists" and the right functor will be "for all".
| {$\exists_X:\Omega^X\rightarrow\Omega$}, {$\exists_XP=\top\Leftrightarrow$}{$\exists x\in X(P(x)=\top)$} | dummy variable constant functor {$\Delta_X:\Omega\rightarrow\Omega^X$} which sends {$\top$} to {$\top(x)=\top$} and sends {$\bot$} to {$\bot(x)=\bot$} | {$\forall_X:\Omega^X\rightarrow$}{$\Omega$}, {$\forall_XP=\top\Leftrightarrow$}{$\forall x\in X(P(x)=\top)$} | {$\bot\leq\top,\Omega=\{\bot,\top\},\Omega^X$} is the set of propositional functions {$P:X\rightarrow\Omega$}. {$P\leq Q\Leftrightarrow$}{$\forall X(P\Rightarrow Q)$} (Yoneda embedding for preorders). |
| {$\exists_f:\textrm{Sub}(X)\rightarrow$}{$\textrm{Sub}(Y)$} closes {$X$} in {$X\times_Y T$} and returns the thereby specified subset of {$Y$} | {$f^*:\textrm{Sub}(Y)\rightarrow$} \textrm{Sub}(X)$} maps subobjects {$T$} of {$Y$} to the pullback {$X\times_Y T$}. | {$\forall_f:\textrm{Sub}(X)\rightarrow$}{$\textrm{Sub}(Y)$} closes {$X$} in {$X\times_Y T$} and returns the thereby specified subset of {$Y$} | Given morphism {$f:X\rightarrow Y$} in a category with pullbacks. {$\textrm{Sub}(X)$} is the category that is the preorder of subobjects. |
| {$\Sigma_F$} Union (sums up) data | {$\Delta_F$} duplicate or destroy tables or columns, turns {$\mathcal{D}$}-instances into {$\mathcal{C}$}-instances. | {$\Pi_F$} product, pairs and queries data | Given {$F:C\rightarrow D$} Seven Sketches 3.4.3 |
Schulman: Now we define “{$P$} or {$Q$}” to be {$\left \| P+Q \right \|$}, and similarly “there exists an {$x : A$} such that {$P(x)$}” to be {$\left \| \sum_{x:A} P(x) \right \|$}. As observed by Lawvere [73], this definition of the existential quantifier can be described categorically as the left adjoint to pullback between posets of subobjects {$\textrm{Sub}(\left \| \Gamma \right \|) \rightarrow$}{$ \textrm{Sub}(\left \| \Gamma,x:A \right \|)$}. The untruncated {$\sum_{x:A}$} gives the left adjoint to the pullback between slice categories {$\mathbf{Ctx}_{\left \| \Gamma \right \|}\rightarrow$}{$ \mathbf{Ctx}_{\left \| \Gamma,x:A \right \|}$}, and the truncation reflects it back into monomorphisms. Similarly, the universal quantifier “for all x : A, P(x)” is the right adjoint of the same functor: since the right adjoint {$\prod_{x:A}$} between slice categories already preserves monomorphisms, no truncation is necessary.
| Left-Left | Left | Center | Right | Right-right | Notes |
| {$\Lambda$} | {$\Pi$} | {$\Delta$} maps set {$A$} to the presheaf {$\Delta A$} with constant value {$A$} | {$\Gamma$} | {$\nabla$} | Between {$\mathbf{Set}$} and presheaves {$[\mathscr{O}(X)^{\textrm{op}},\mathbf{Set}]$} (of open subsets {$\mathscr{O}(X)$}) on topological space {$X$}, Leinster, page 50 |
See: nLab: Necessity and possibility for examples.
- In a context of pure logic this would be called existential quantifier ⊣ context extension ⊣ universal quantifier
- In a context of dependent type theory this would be called dependent sum ⊣ context extension ⊣ dependent product.
- In propositional modal logic, with {$T = \Diamond$} “possibility” and {$G = \Box$} “necessity,” where the adjointness {$\Diamond\vdash\Box$} is equivalent to the law known to modal logicians as S5. (Awodey, 10.4)
Given a group {$G$}, a (left) G-set is a pair {$(X,\rho)$} where {$X$} is a set and the action of {$G$} on {$X$} is the map {$\rho :G\times X\rightarrow G$}, where {$\rho(g,x) =g\cdot x= gx$}. Consider the category of G-sets and the category of sets. A morphism in the category of G-sets is a G-map {$f:X\rightarrow Y$} such that {$f(g\cdot x)=g\cdot f(x)$} for all {$g\in G$} and {$x\in X$}.
- Given a set S, combine it with the trivial action to yield a G-set. This has left and right adjoints.
- The left adjoint maps the G-set X to the set {$X^G$} of fixed points.
- The right adjoint maps the G-set X to {$X/G$}, the orbit set of X under G, which is the set of equivalences classes (orbits) of the equivalence relation {$R=\{(x,gx)|x\in X, g\in G\}$} whereby {$x\sim gx$}. The class of {$x$} is {$Gx=\{gx | g\in G\}$} and is called the orbit through {$x$}.
Yoneda embedding
Yoneda embedding is the embedding of a category {$\mathcal{C}$} into {$\mathbf{Set}$} as follows:
{$\mathcal{C}(A,B) \simeq \mathbf{Set}(\mathcal{C}(-,B),\mathcal{C}(-,A))$}
So we can think of the Yoneda embedding as a fully faithful functor {$Z:\mathcal{C}\rightarrow \mathbf{Set}^{\mathcal{C}}$} which sends {$X$} to the functor {$\mathcal{C}(-,X)$} and which sends {$f:X\rightarrow Y$} to the natural transformation which sends functor {$\mathcal{C}(-,Y)$} to {$\mathcal{C}(-,X)$} by prepending {$f$}.
nLab: Adjoint string There is an adjoint 5-tuple between {$[Set^{op}, Set]$} and {$Set$}. Indeed, given a locally small category B, and the Yoneda embedding, {$Y: B \to [B^{op}, Set]$}, then Y being the rightmost functor of an adjoint 5-tuple entails that B is equivalent to Set; see Rosebrugh, Wood. An Adjoint Characterization of the Category of Sets and also Ross Street, Robert Walters. Yoneda Structures on 2-Categories.
Related chat on the Category Theory Zulip server
Preorders. Based on function f.
| Direct image {$\textrm{im}(f):\mathcal{P}(A)\rightarrow\mathcal{P}(B)$} is defined by {$\textrm{im}(f)(U)=$}{$\{b\in B|(\exists a\in U)(f(a)=b)\}$} | Inverse image {$f^{-1}:\mathcal{P}(A)\rightarrow\mathcal{P}(B)$} is defined by {$f^{-1}(V)=$}{$\{a\in A|f(a)\in V\}$} | Given set function {$f:A\rightarrow B$} Awodey Example 9.12 |
| {$f^{-1}:\mathcal{P}(A)\rightarrow\mathcal{P}(B)$} | Dual image {$f_*(U):\mathcal{P}(A)\rightarrow\mathcal{P}(B)$} where {$f_*(U)=$}{$\{b\in B|(\forall a\in A)(f(a)=b\Rightarrow a\in U\}$} | Given set function {$f:A\rightarrow B$} Awodey Example 9.12 |
| Direct image {$\textrm{im}(f):\mathcal{O}(A)\rightarrow\mathcal{O}(B)$} is defined by {$\textrm{im}(f)(U)=$}{$\{b\in B|(\exists a\in U)(f(a)=b)\}$} | Inverse image {$f^{-1}:\mathcal{P}(A)\rightarrow$}{$\mathcal{P}(B)$} is defined by {$f^{-1}(V)=\{a\in A|f(a)\in V\}$} | Given continuous function {$f:A\rightarrow B$} and considering the sets of open subsets as categories (preorders) {$\mathcal{O}(A)$} and {$\mathcal{O}(B)$} Awodey Example 9.12 |
If {$f:X\rightarrow Y$} is a function, then for any subset {$M$} of {$X$} we can form the image F(M) {$=$} f M {$=$} {f(m) | m ∈ M} and for any subset {$N$} of {$Y$} we can form the inverse image {$G(N)=f^{-1}N = \{x\in X | f(x)\in N\}$}. Then {$F$} and {$G$} form a monotone Galois connection between the power set of {$X$} and the power set of {$Y$}, both ordered by inclusion ⊆. There is a further adjoint pair in this situation: for a subset {$M$} of {$X$}, define H(M) {$=$} {y ∈ Y | {$f^{-1}$}{y} ⊆ M}. Then {$G$} and {$H$} form a monotone Galois connection between the power set of {$Y$} and the power set of {$X$}. In the first Galois connection, {$G$} is the upper adjoint, while in the second Galois connection it serves as the lower adjoint.  Galois connection
Galois connection
In the case of a quotient map between algebraic objects (such as groups), this connection is called the lattice theorem: subgroups of {$G$} connect to subgroups of {$G/N$}, and the closure operator on subgroups of {$G$} is given by {$\overline{H}=HN$}.
| Direct image functor {$f_*:Sh(X)\rightarrow Sh(Y)$} | Inverse image functor {$f^*:Sh(Y)\rightarrow Sh(X)$} | Defined with regard to a continuous function from topological space {$X$} to topological space {$Y$}. {$Sh(X)$} and {$Sh(Y)$} are Grothendieck toposes. |
Note that if {$f$} is both surjective and injective, then we have that the direct image functor is not only the left adjoint of the inverse image functor but also the right adjoint.
- Given toposes {$E$}, {$F$}, a geometric function consists of a pair of adjoint functors (inverse image){$f^*:F\rightarrow E:f_*$}(direct image) such that {$f^*$} preserves finite limits.
- If the inverse image {$f^*$} has a left adjoint {$f^!:E\rightarrow F$}, then {$f$} is an essential geometric morphism.
- We can define the adjunction (left and right) in the opposite direction, which might be thought of as an algebraic morphism. This is related to the Isbell duality.
- See nLab: Special classes of geometric morphisms such as global sections, geometric embedding, base change...
Morgan Rogers. Using Topos Theory to Make Analogies Precise. Examples of {$LH/X \leftrightarrow \textrm{Set}$} and {$\textrm{PSH}(M) \leftrightarrow \textrm{Set}$}
- Any Grothendieck topos has a unique geometric morphism to the topos of sets (an adjunction where the left adjoint preserves finite limits).
- Consider the maps from the terminal object to any other object. The functor {$\Gamma$} sends those maps to their set. Consider the map {$\Delta$} that sends a set {$A$} to the disjoint union indexed by {$A$} of copies of the trivial object (?)
- The global sections functor {$\Gamma$} maps the set of global sections to that set. Its left adjoint is the constant map {$\Delta$} which sends a set {$A$} to the disjoint union indexed by {$A$} of copies of {$X$}.
- There can be an extra adjoint {$C$} that can indicate a locally connected topos.
| direct image functor {$f_*:PA\rightarrow PB$} maps subset {$A′⊂A$} to subset {$f(A′)⊂B$}. Then for {$A′⊂A$} and {$B′⊂B$}, {$f(A′)⊂B′$} if and only if {$A′⊂f^{−1}(B′)$} | inverse image functor {$f^{-1}:PB\rightarrow PA$} | {$f_!:PA\rightarrow PB$} maps {$A′⊂A$} to the subset of elements of {$B$} whose fibers (inverse images) lie entirely in {$A'$}. Thus {$B′⊂f_!(A′)\Leftrightarrow f^{−1}(B′)⊂A′$} | given set function {$f:A\rightarrow B$}, the subsets of {$A$} and subsets of {$B$} for posets, {$PA$} and {$PB$}, ordered by inclusion. |
| left Kan extension {$f_!$} | precomposition functor {$f^∗:Sets^{D^{op}}→Sets^{C^{op}}$} given by {$f^∗(Q)(C)=Q(fC)$} | right Kan extension {$f_∗$} | Awodey 9.17 |
| {$f^{-1}$} | inverse image (or pullback functor on sheaves) {$f^*:\textrm{Sh}(Y)\rightarrow \textrm{Sh}(X)$} | direct image (or pushforward functor on sheaves) {$f_*:\textrm{Sh}(X)\rightarrow \textrm{Sh}(Y)$} | (understand the case for sheaves) |
In the adjunction {$f^{-1} \vdash f_*$}, the left adjoint for coherent sheaves will differ from that for sheaves (of sets). Examples
For {$f:X→Y$} a morphism of sites coming from a functor {$f^t:S_Y→S_X$} of the underlying categories, the left Kan extension of functors along {$f^t$} is the inverse image operation {$f^{−1}:\textrm{PSh}(Y)→\textrm{PSh}(X)$}. nLab
{$f_*\dashv f^{-1}$} expresses perfect duality. The trivial functor is {$f_*$} which is aggregation.
Any object {$f:B\rightarrow A$} of a slice category {$C/A$} has a universal property: it is the image of the terminal object {$1_B:B\rightarrow B$} of {$C/B $} under the left adjoint {$f!:C/B\rightarrow C/A$} to pullback along {$f$}.
- A context of six operations {$(f_! \dashv f^!)$}, {$(f^\ast \dashv f_\ast)$} induces an adjoint triple when either {$f^! \simeq f^\ast$} or {$f_! = f_\ast$}. This is called a Wirthmüller context or a Grothendieck context, respectively.
- {$f_! \dashv f^! \simeq f^\ast \dashv f_\ast$} Wirthmüller context
- {$f^\ast \dashv f_\ast = f_! \dashv f^!$} Grothendieck context
| the proper (or extraordinary) direct image {$f_!:Sh(X) → Sh(Y)$} | the proper (or extraordinary) inverse image {$f^!:D(Sh(Y)) → D(Sh(X))$} |
Compact support (relevant for the exceptional functors) suggests a connection with "anything" and "something".
Derivators are the axiomatization of prederivators which come equipped with adjoint functors {$f^? \dashv f_! \dashv f^* \dashv f_* \dashv f^!$} Heuristically, <math>f_*</math> should correspond to inverse limits, <math>f_!</math> to colimits.
Flatness
See: Flatness and Inverse image functor. {$f^{*}$} is (in general) only right exact. If {$f^{*}$} is exact, f is called flat.
Locales and frames
 Complete Heyting algebra: Frames and locales The relation of locales and their maps to topological spaces and continuous functions may be seen as follows. Let {$f: X\to Y$} be any map. The power sets P(X) and P(Y) are complete Boolean algebras, and the map {$f^{-1}: P(Y)\to P(X)$} is a homomorphism of complete Boolean algebras. Suppose the spaces X and Y are topological spaces, endowed with the topology O(X) and O(Y) of open sets on X and Y. Note that O(X) and O(Y) are subframes of P(X) and P(Y). If {$f$} is a continuous function, then {$f^{-1}: O(Y)\to O(X)$}
Complete Heyting algebra: Frames and locales The relation of locales and their maps to topological spaces and continuous functions may be seen as follows. Let {$f: X\to Y$} be any map. The power sets P(X) and P(Y) are complete Boolean algebras, and the map {$f^{-1}: P(Y)\to P(X)$} is a homomorphism of complete Boolean algebras. Suppose the spaces X and Y are topological spaces, endowed with the topology O(X) and O(Y) of open sets on X and Y. Note that O(X) and O(Y) are subframes of P(X) and P(Y). If {$f$} is a continuous function, then {$f^{-1}: O(Y)\to O(X)$}preserves finite meets and arbitrary joins of these subframes. This shows that O is a functor from the category Top of topological spaces to Loc, taking any continuous map {$f: X\to Y$} to the map {$O(f): O(X)\to O(Y)$} in Loc that is defined in Frm to be the inverse image frame homomorphism {$f^{-1}: O(Y)\to O(X).$} Given a map of locales {$f: A\to B$} in Loc, it is common to write {$f^*: B\to A$} for the frame homomorphism that defines it in Frm. Using this notation, {$O(f)$} is defined by the equation {$O(f)^* = f^{-1}.$}
Conversely, any locale A has a topological space S(A), called its spectrum, that best approximates the locale. In addition, any map of locales {$f: A\to B$} determines a continuous map {$S(A)\to S(B).$} Moreover this assignment is functorial: letting P(1) denote the locale that is obtained as the power set of the terminal set {$1=\{*\},$} the points of S(A) are the maps {$p: P(1)\to A$} in Loc, i.e., the frame homomorphisms {$p^*: A\to P(1).$}
For each {$a\in A$} we define {$U_a$} as the set of points {$p\in S(A)$} such that {$p^*(a) =\{*\}.$} It is easy to verify that this defines a frame homomorphism {$A\to P(S(A)),$} whose image is therefore a topology on S(A). Then, if {$f: A\to B$} is a map of locales, to each point {$p\in S(A)$} we assign the point {$S(f)(q)$} defined by letting {$S(f)(p)^*$} be the composition of {$p^*$} with {$f^*,$} hence obtaining a continuous map {$S(f): S(A)\to S(B).$} This defines a functor {$S$} from Loc to Top, which is right adjoint to O.
Any locale that is isomorphic to the topology of its spectrum is called spatial, and any topological space that is homeomorphic to the spectrum of its locale of open sets is called sober. The adjunction between topological spaces and locales restricts to an equivalence of categories between sober spaces and spatial locales.
- The article on
 Stone duality describes an adjunction between the category of topological spaces and the category of sober spaces that is known as soberification. Notably, the article also contains a detailed description of another adjunction that prepares the way for the famous duality of sober spaces and spatial locales, exploited in pointless topology.
Stone duality describes an adjunction between the category of topological spaces and the category of sober spaces that is known as soberification. Notably, the article also contains a detailed description of another adjunction that prepares the way for the famous duality of sober spaces and spatial locales, exploited in pointless topology.
Any function that preserves all joins (and hence any frame homomorphism) has a right adjoint, and, conversely, any function that preserves all meets has a left adjoint. Hence, the category Loc is isomorphic to the category whose objects are the frames and whose morphisms are the meet preserving functions whose left adjoints preserve finite meets. This is often regarded as a representation of Loc, but it should not be confused with Loc itself, whose morphisms are formally the same as frame homomorphisms in the opposite direction.
nLab: Motivation for cohesive topos
- expresses cohesion of geometry
- For cohesive topos by definition the terminal geometric morphism extends to an adjoint quadruple.
- Cohesion specifies how points in a space cohere like a droplet. For example, an open ball of points is a cohesive droplet for a topological space or manifold. This generalizes a basis of a topology.
- Should have {$\Pi(\textrm{Disc}(S))=S$}.
| {$f_!$} | {$f^*$} | {$f_*$} | {$f^!$} | |
| {$Π:H\rightarrow\textrm{Set}$} sends space {$X$} to its set of cohesively connected components. For instance, a single open ball is sent to a singleton {$\{*\}$}. | {$\textrm{Disc}(S)$} is the space created by regarding every element of S as a disconnected point, droplet. | The forgetful functor {$Γ$} forgets the space and returns the underlying set of points. | {$\textrm{coDisc}(S)$} regards all of S as one single big droplet | Between {$H$}, a collection of spaces, and {$\textrm{Set}$} |
For any category C, there is a functor {$ids: C\to Ar(C)$} from C to its arrow category that assigns the identity morphism of each object. This functor always has both a left and a right adjoint which assign the codomain and domain of an arrow respectively; thus we have an adjoint triple {$cod \dashv ids \dashv dom$}. If C has an initial object 0, then cod has a further left adjoint I assigning to each object x the morphism {$0\to x$}; and dually if C has a terminal object 1 then dom has a further right adjoint T assigning to x the morphism {$x\to 1$}. Thus if C has an initial and terminal object, we have an adjoint 5-tuple.
Continuing from the last example, if C is moreover a pointed category (has a zero object, that is, an initial object and terminal object that are isomorphic) with pullbacks and pushouts, then I has a further left adjoint that constructs the cokernel of a morphism {$x\to y$}, i.e. the pushout of {$y \leftarrow x \to 0$}; and T has a further right adjoint that constructs the kernel of a morphism {$x \to y$}, namely the pullback of {$x\to y \leftarrow 0$}. Thus we have an adjoint 7-tuple. In fact, the existence of such an adjoint 7-tuple characterizes pointed categories among categories with finite limits and colimits.
The previous two examples apply also to derivators, and the extension of the analogous adjoint 5-tuple to a 7-tuple again characterizes the pointed derivators. Moreover, the stable derivators are characterized by the extension of this 7-tuple to a doubly-infinite adjoint string with period 6 (GrothShul17).
Moritz Groth, Mike Shulman. Generalized stability for abstract homotopy theories
- We show that a derivator is stable if and only if homotopy finite limits and homotopy finite colimits commute, if and only if homotopy finite limit functors have right adjoints, and if and only if homotopy finite colimit functors have left adjoints. These characterizations generalize to an abstract notion of "stability relative to a class of functors", which includes in particular pointedness, semiadditivity, and ordinary stability. To prove them, we develop the theory of derivators enriched over monoidal left derivators and weighted homotopy limits and colimits therein.
Diagram. Limit functor and colimit functor.
Diagonal functor
The diagonal functor preserves both limits and colimits, thus has both a left adjoint and a right adjoint. This adjoint string expresses the relationship between internal structure (colimits) and external relationships (limits).
| Left adjoint | Diagonal functor | Right adjoint | Notes |
| sum functor | diagonal functor {$\Delta:\textbf{C}\rightarrow$}{$ \textbf{C}\times \textbf{C}$} | product functor | Accordingly as to whether {$\textbf{C}$} has sums and products |
| colimit functor {$\textrm{lim}:\textbf{C}^J\rightarrow \textbf{C}$} | diagonal functor {$\Delta:C\rightarrow C^J$} | limit functor {$\textrm{lim}:\textbf{C}^J\rightarrow \textbf{C}$} | Accordingly as to whether every diagram of shape J has a colimit and limit. {$\textrm{Hom}(\textrm{colim} F,N)\cong$}{$ \textrm{Cocone}(F,N)$} {$\textrm{Hom}(N,\textrm{lim} F)\cong \textrm{Cone}(N,F)$} |
| {$F:\mathbb{Ab}^2\rightarrow \mathbb{Ab}$} assigns to every pair {$(X_1, X_2)$} of abelian groups their direct sum {$X_1+X_2$} | {$G:\mathbb{Ab}\rightarrow$}{$ \mathbb{Ab}^2$} is the functor which assigns to every abelian group {$Y$} the pair {$(Y, Y)$} | Analogous examples are given by other coproducts: direct sum of vector spaces, direct sum of modules, free product of groups, disjoint union of sets. | |
| Join {$\vee : X \times X \rightarrow X$}, {$(x,y)\rightarrow x\vee y$} (if all binary joins exist) | {$q: X \rightarrow X \times X$} given by {$q(x) = (x, x)$} | Meet {$\wedge : X \times X \rightarrow X$}, {$(x,y)\rightarrow x\wedge y$} (if all binary meets exist) | Preorders. Note that the Meet = Tensor has a right adjoint Hom if we fix one factor. |
| Cokernel functor {$L:D\rightarrow Ab$} maps homomorphism to its cokernel. | {$F:Ab\rightarrow D$} maps abelian group {$A$} to homomorphism {$A\rightarrow 0$} | {$G:D\rightarrow Ab$} maps homomorphism to its kernel. | {$Ab$} is the category of abelian groups, {$D$} is the category of homomorphisms of abelian groups. This expresses the universal property of kernels.  Examples Similarly for vector spaces and for modules. Examples Similarly for vector spaces and for modules. |
Instead of the diagonal functor, we can map C into various diagrams and get a similar result. Also:
| {$R:1\rightarrow C$} maps to terminal object {$r$} | {$t:C\rightarrow 1$} unique functor from category {$C$} to the terminal category | {$L:1\rightarrow C$} maps to initial object {$s$} | See Spivak 2013, pg.208, Example 5.1.2.1 |
| Map to least element {$j^l:1\rightarrow X$} | Constant map {$j:X\rightarrow 1=\{*\}$} where {$j(x)=*$} | Map to greatest element {$j^g:1\rightarrow X$} | Terminal object is trivial poset {$1=\{*\}$}, poset {$X$}. {$j(x)=*\leq * \Rightarrow x\leq j^g(*) $} Galois connection.  Completeness in terms of adjunctions Completeness in terms of adjunctions |
Note also that the empty category is the initial object in {$Cat$}.
More examples at  Adjoint functors
Adjoint functors
- Any limit functor is right adjoint to a corresponding diagonal functor (provided the category has the type of limits in question), and the counit of the adjunction provides the defining maps from the limit object (i.e. from the diagonal functor on the limit, in the functor category).
- Any colimit functor is left adjoint to a corresponding diagonal functor (provided the category has the type of colimits in question), and the unit of the adjunction provides the defining maps into the colimit object.
Kan extensions
Data migration and Kan extensions
- Tai Danae Bradley
- Seven Sketches in Compositionality Section 3.4, Adjunctions and Data Migration
- John Baez on Kan extensions in his course.
If, for fixed {$K:C\rightarrow D$} and {$E$}, the left {$\textrm{Lan}_K$} and right {$\textrm{Ran}_K$} Kan extensions of any functor {$F: C\rightarrow E$} along {$K$} exist, then these define left and right adjoints to the pre-composition functor {$K^∗: E^D\rightarrow E^C$}. Riehl 6.1.5
Richard Southwell. Category Theory for Beginners: Kan Extensions.
- The category of graphs {$\textrm{Set}^{A}$} where {$A$} is the category with two objects, edges E and vertices V, and two nontrivial morphisms target {$t:E\rightarrow V$} and source {$s:E\rightarrow V$}.
- {$\Sigma$} is left adjoint to {$\Delta:\textrm{Set}\rightarrow \textrm{Set}^{A}$} (defined before 35:00), which is left adjoint to {$\Pi$} (46:00). {$\Sigma$} goes from Graphs to Sets and takes a graph to a set with one element for each weakly connected component in the graph. And diagonalization {$\Delta$} goes from Sets to Graphs by converting each element to an object with an identity arrow. {$\Pi$} sends a graph to its set of points (self-loops).
For C'= the point (the category with a single object and a single morphism), the right Kan extension of F is the limit of F, {$\textrm{Ran}F≃\textrm{lim}F$} and the left Kan extension is the colimit {$\textrm{Lan}F≃\textrm{colim}F$}. Nlab
Kan extension of adjoint pair is adjoint quadruple.
Kan extensions
- “Explain how all other universal constructions, in particular limits and adjunctions, are subsumed by that of Kan extensions and clarify to what extent the reverse is true!” The notion of Kan extensions allows understanding all other fundamental definitions of category theory, (co-)limits, adjunctions, (co-)ends, as special cases of just one universal construction: finding an optimal solution to the problem of extending a functor from a “subcategory” to the whole category. [Rie17, Chpt. 6]
Preservation of limits and colimits
| Left adjoint | Right adjoint | Notes |
| F preserves small colimits | F is a functor between locally presentable categories | |
| G preserves small limits and is an accessible functor | G is a functor between locally presentable categories |
- Left adjoint exists for functor that preserves limits. Right adjoint exists for functor that preserves colimits.
- Adjoint functors: Limit preservation Every functor that has a left adjoint (and therefore is a right adjoint) is continuous (i.e. commutes with limits in the category theoretical sense); every functor that has a right adjoint (and therefore is a left adjoint) is cocontinuous (i.e. commutes with colimits).
- Exact functor If the functor F is left adjoint to G, then F is right exact and G is left exact.
Tensor product. Internal Hom.
Ideas
Hom functor outputs values in Set, whereas Internal Hom outputs values in the category C. They both take inputs from {$C^{op}\times C$}. A category with Internal Hom is called a closed category. They are closely related to the Yoneda lemma. Examples include cartesian closed categories (Set, or any topos), compact closed categories (notably finite dimensional vector spaces FdVect), monoidal closed categories.
Tensor product increases slack because it makes all of the factors equally available. Internal Hom decreases slack because it tucks them away one by one in a definite order.
Tensor product expresses geometry (homogeneous choice). Internal Hom expresses algebra (thinking step-by-step).
- Tensor product - thinking-in-parallel - homogeneity of choice (geometry). Homset - thinking-in-series - step-by-step (algebra).
- The tensor product - homset adjunction is based on an existing object which it extends either externally or internally.
- MathStackExchange: Proof of Adjointness of Hom and Tensor
- HomSet expresses choice.
- The left adjoint tensor product is like geometry ("homogeneity of choice") and the right adjoint homset is like algebra ("step by step").
- The tensor-curry adjunction relates all and one, as between everything and anything, and between nothing and something. It allows for step-by-step algebra, as by the Yoneda lemma.
The simplest case: Product vs. Exponential Object
Suppose that we have a cartesian closed category {$C$}, which is to say, for any two objects {$V$} and {$W$}, there exists the product {$V\times W$} and the exponential object {$V^W$}. Then we have the following adjunction.
| Product functor {$\_\times A:C\rightarrow C$} sends {$X\rightarrow X\times A$} and {$(h:X\rightarrow Y)\rightarrow$}{$ (h\times 1_A:X\times A\rightarrow Y\times A)$} | Exponential object functor {$U:C\rightarrow C$} sends {$Y\rightarrow Y^A$} and {$(g:Y\rightarrow Z)\rightarrow (g^A:Y^A\rightarrow Z^A)$} | This is the general case for a cartesian closed category |
| Product functor for sets | Exponential object {$Y^A = \{f:A\rightarrow Y\}$} | The category {$\mathbf{Set}$}. The map {$\textrm{eval}:(Y^A\times A)\rightarrow Y$} sends the pair {$(f,a)$} to {$f(a)$}. And for any map {$g:X\times A\rightarrow Y$} the map {$\lambda g:X\rightarrow Y^A$} is the curried form of {$g$}, namely: {$\lambda g(x)(a)=g(x,a)$}. |
| {$(\_\wedge A)$} | {$(\_)^A$} is the Heyting implication {$(A\Rightarrow \_)$} | Heyting algebra is a bounded lattice that has all exponential objects. Awodey 9.13 the bicondition is {$p\wedge q\leq r :: p\leq q\Rightarrow r$} Heyting algebra can be formulated entirely in terms of adjoints. |
| {$Y^A$} exists provided that {$A$} is a locally compact Hausdorff space. Then {$Y^A$} is the set of continuous functions from {$A$} to {$Y$} together with the compact-open topology. | Category of topological spaces |
Modules of rings
Note that here we can be dealing with modules of different rings {$R$} and {$S$} so that we have {$\textrm{Hom}_S(Y\otimes_R X,Z)\cong\textrm{Hom}_R(Y,\textrm{Hom}_S(X,Z))$}
| {$- \bigotimes_R X:\textrm{Mod}_S\rightarrow\textrm{Mod}_R$} | {$\textrm{Hom}_S(X,-):\textrm{Mod}_R\rightarrow\textrm{Mod}_S$} | Note that the {$(R,S)$}-bimodule {$X$} is fixed. {$\textrm{Mod}_S$} and {$\textrm{Mod}_R$} are right modules. And the direction of the arrow switches. There is a natural isomorphism {$\textrm{Hom}_S(Y\bigotimes_R X, Z) \cong$}{$ \textrm{Hom}_R(Y,\textrm{Hom}_S(X,Z))$} Tensor-Hom adjunction |
| internal tensor product | internal Hom functor | |
| smash product | smash-hom adjunction | topological spaces with chosen base points, Tai Danae Bradley |
| currying f(a,b) to create two functions in sequence x=h(b) where h=g(a) | uncurrying | |
| functor {$B ↦ B × C$} | functor {$A ↦ A^C$} | Currying: Set theory for every fixed set C |
| {$L:=X\times –:\mathbf{Set}\rightarrow$}{$\mathbf{Set}$} | {$R:=\mathbf{Set}(X,–):\mathbf{Set}\rightarrow$}{$\mathbf{Set}$} | Product-hom adjunction, see Topology: A Categorical Approach. Page 92. Note that {$\mathbf{Set}(LZ,Y)=$}{$Y^{X\times Z}\cong$}{$ (Y^X)^Z = \mathbf{Set}(Z,RY)$} |
| {$I\times \_$} | {$(\_)^I$} | Cylinder free-path adjunction. Algebraic Topology: A Categorical Approach 6.1. {$I=[0,1]$} |
| Conjunction {$F(x)=a\vee x$} | Implication {$G(y)=y\wedge\not a = a\rightarrow y$} | {$F:2^U\rightarrow 2^U:G$} Fix a. Boolean algebra. A case of the tensor-hom adjunction. |
| Meet (conjunction) {$\_\wedge Y$} | Implication {$Y\Rightarrow\_$} | {$F:2^U\rightarrow 2^U:G$} Fix Y. Propositional logic, Heyting algebra |
| Intersection {$F(M) = L ∩ M $} | Implication {$G(N) = N ∪ (U \ L) =$}{$ (L ∩ N) ∪ (U \ L)$} Intersection + Complement of {$L$} | {$F:2^U\rightarrow 2^U:G$} General case of preorder. Fix L. |
- Heyting algebra. Implication is right adjoint to meet. {$(-\wedge Y)\dashv (Y\Rightarrow -)$} Product vs. homset.
- The category Cat is Cartesian closed, so for any category C the functors (−)×C and [C,−] describe adjoints from Cat to Cat. Geoff Mar
Kurz, Velebil. Enriched logical connections
- Adjunctions of the form {$L\dashv R : Sp^{op}\rightarrow Alg$} between the dual of the category Spa of “spaces” and the category Alg of “algebras” that arise from a object {$\Omega$}, which is both an “algebra” and a “space”.
For a fixed set of “states” S, the {$(S×−⊣(−)^S)$}-adjunction induces a monad {$(S×−)^S$} on Set called the state monad. This is a commonly used monad in computer science. In functional programming languages such as Haskell, states can be used to model “side effects” of computations. (nLab, Monad)
HoTT Book page 101: pair types also have a universal property for “mapping out”, which may look less familiar. In the case of cartesian products, the nondependent version simply expresses the cartesian closure adjunction: ((A × B) → C) ≃ (A → (B → C)).
nLab: Yoneda Lemma (Yoneda embedding is adjunct of hom-functor) The Yoneda embedding functor {$y:𝒞→[𝒞^{op},\textrm{Set}]$} from Def. 2.1 is equivalently the adjunct of the hom-functor {$\textrm{Hom}_𝒞:𝒞^{op}×𝒞⟶\textrm{Set}$} under the product category/functor category adjunction {$\textrm{Hom}(C^{op}×C,\textrm{Set})\overset{≃}{→}\textrm{Hom}(C,[C^{op},\textrm{Set}])$} in the closed symmetric monoidal category of categories.
Hom functor has right adjoint
| suspension functor {$\Sigma$} | loop space functor {$\Omega$} | classifying space construction | case of circle {$S^1$}, Tai Danae Bradley, proof that fundamental group of circle is Z |
In Bott periodicity, the double loop space {$\Omega^{2}BU$} is essentially {$BU$} again, and likewise {$\Omega^{8}BO$} is essentially {$BO$} again.
Currying: Logic Under the Curry–Howard correspondence, the existence of currying and uncurrying is equivalent to the logical theorem {$(A\land B)\to C\Leftrightarrow A\to (B\to C)$}, as tuples (product type) corresponds to conjunction in logic, and function type corresponds to implication.
Currying: Category Theory In closed monoidal categories: Currying is the statement that the tensor product and the internal Hom are adjoint functors; that is, for every object B there is a natural isomorphism: {$\mathrm {Hom} (A\otimes B,C)\cong \mathrm {Hom} (A,B\Rightarrow C)$}
Here, Hom denotes the (external) Hom-functor of all morphisms in the category, while {$ B\Rightarrow C$} denotes the internal hom functor in the closed monoidal category. For the category of sets, the two are the same. When the product is the cartesian product, then the internal {$ B\Rightarrow C$} becomes the exponential object {$ C^{B}$}.
Currying can break down in one of two ways. One is if a category is not closed, and thus lacks an internal hom functor (possibly because there is more than one choice for such a functor). Another ways is if it is not monoidal, and thus lacks a product (that is, lacks a way of writing down pairs of objects). Categories that do have both products and internal homs are exactly the closed monoidal categories.
The setting of cartesian closed categories is sufficient for the discussion of classical logic; the more general setting of closed monoidal categories is suitable for quantum computation.
The difference between these two is that the product for cartesian categories (such as the category of sets, complete partial orders or Heyting algebras) is just the Cartesian product; it is interpreted as an ordered pair of items (or a list). Simply typed lambda calculus is the internal language of cartesian closed categories; and it is for this reason that pairs and lists are the primary types in the type theory of LISP, scheme and many functional programming languages.
By contrast, the product for monoidal categories (such as Hilbert space and the vector spaces of functional analysis) is the tensor product. The internal language of such categories is linear logic, a form of quantum logic; the corresponding type system is the linear type system. Such categories are suitable for describing entangled quantum states, and, more generally, allow a vast generalization of the Curry–Howard correspondence to quantum mechanics, to cobordisms in algebraic topology, and to string theory.[1] The linear type system, and linear logic are useful for describing synchronization primitives, such as mutual exclusion locks, and the operation of vending machines.
Commuting with both limits and colimits. See: Exact functor and consider the difference between left exact functors and right exact functors.
Akhil Mathew Having an adjoint tells you that the functor commutes with (either) limits or colimits. If a functor has a left adjoint, then it commutes with colimits, while if it has a right adjoint, it commutes with limits. For nice categories, one can sometimes conclude the converse. One example of this is in an abelian category. In the case of R-modules, for instance, the adjunction between Hom and the tensor product shows that the tensor product is right-exact (a.k.a. commutes with finite colimits). This is a somewhat more conceptual argument than the usual one.
Cartesian closed categories have binary products and a right adjoint to each functor sending A to AxB, which is essentially the typed lambda-calculus.
See Wikipedia: Currying {$B \mapsto B\times C$} is left adjoint to {$A \mapsto A^C$}. This grounds the equation {$A^{B\times C}\cong (A^C)^B$}.
Akhil Mathew Let X be a locally compact Hausdorff space. Then the functor {$Z↦Z×X$} has an adjoint (namely, the functor {$Y↦YX$}). It follows that taking products with {$X$} preserves push-out diagrams, and more generally all colimits. This is useful sometimes in algebraic topology. For instance, if you have a push-out {$A∪_BC$} and homotopies {$A×I→Z$} and {$C×I→Z$} that agree on {$B×I$}, you get a homotopy {$(A∪_BC)×I→Z$}, the continuity of which might not be immediately obvious otherwise.
- {$Hom_R(A,B)=T(B)$} is a left exact functor from {$Mod-R$} to {$Ab$} and so it has right derived functors {$R^iT(B)=Ext^i_R(A,B)$}.
- {$A\bigotimes_R B=T(A)$} is a right exact functor from {$Mod-R$} to {$Ab$} and so it has left derived functors {$L_iT(A)=Tor^R_i(A,B)$}.
- Tor and Ext. Of particular interest are the derived functors of the tensor product functor of an abelian category, the so-called Tor -functor, and of the hom-functor, the so-called Ext-functor. They have been used to study algebro-topological invariants of, e.g., groups or Lie algebras. [Wei94, § 3.1–§ 3.4], [Bla11, § 11.4–§ 11.5]
- Ext is related to the
 Yoneda product
Yoneda product
- Peter May. Notes on Ext and Tor.
- Math StackExchange. Why is it called adjunction formula?
- page 32
- {$\mathcal{K}_Y\cong\mathcal{K}_X\otimes\mathcal{O}(x)(Y)\otimes\mathcal{O}_Y$}
- page 27. the canonical morphism {$\mathcal{E}\rightarrow(\mathcal{E}^{\vee})^{\vee}$} is adjoint to the evaluation morphism {$\mathcal{E}\otimes_{\mathcal{O}_X}\mathcal{E}^{\vee}\rightarrow\mathcal{O}_X$}
Trivial?
Explain if below is a trivial case of the tensor product - homset adjunction.
| Left adjoint | Right adjoint | Notes |
| {$(-)^*:\mathbf{Vect}_k\rightarrow \mathbf{Vect}^{op}_k$} | {$(-)^*:\mathbf{Vect}^{op}_k\rightarrow \mathbf{Vect}_k$} | each functor send a vector space {$V$} to its dual vector space {$V^*:=\textrm{Hom}(V,k)$} See: Double dualization monad which sends a vector space to its double dual |
| Riehl Ex.5.1.14 similarly discusses the double power set monad |
Free. Forgetful.
Free construction vs. Forgetfulness
- "Free" and "forgetful" are two opposite manifestations of "unrestricted". Like decreasing and increasing slack.
- Forgetfulness, freeness are properties with regard to the two ends of a morphism that restricts it or not, makes it less frequent or not.
- An important application of the Adjoint Functor Theorem is that any equational theory T gives rise to a free a forgetful adjunction between Sets and the category
of models of the theory, or “T -algebras.” (Awodey, 9.37)
- let T be a (finitary) equational theory, consisting of finitely many operation symbols, each of some finite arity (including 0-ary operations, that is, constant symbols), and a set of equations between terms built from these operations and variables. For instance, the theory of groups has a constant {$u$} (the group unit), a unary operation {$g^{−1}$} (the inverse), and a binary operation {$g · h$} (the group product), and a handful of equations such as {$g · u = g$}. The theory of rings has a further binary operation and some more equations. The theory of fields is not equational, however, because the condition {$x \neq 0$} is required for an element {$x$} to have a multiplicative inverse.
- A T -algebra is a set equipped with operations (of the proper arities) corresponding to the operation symbols in T, and satisfying the equations of T . A homomorphism of T -algebras {$h: A → B$} is a function on the underlying sets that preserves all the operations, in the usual sense.
- Let {$T-Alg$} be the category of all such algebras and their homomorphisms. There is an evident forgetful functor {$U : T-Alg → Sets$}. The Adjoint Functor Theorem implies that this functor always has a left adjoint F , the “free algebra” functor.
- Every monad arises from some adjunction, namely the free–forgetful adjunction: {$T(-):C\rightleftarrows C^{T}:{\text{forget}}$} whose left adjoint sends an object {$X$} to the free T-algebra {$T(X)$}. {$C^T$} is the Eilenberg-Moore category. This adjunction is a terminal object in the category {$\textfb{Adj}(C,T)$}.
- For any equational theory T, the forgetful functor from T algebras to Sets has a left adjoint. (Awodey, 9.38)
- The category of algebras for an equational theory T always has a “free T -algebra” functor, left adjoint to the forgetful functor into Sets. This adjunction describes the notion of a T-algebra in a way that is independent of the specific syntactic description given by the theory T , the operations and equations of which are rather like a particular presentation of that notion. In a certain sense that we are about to make precise, it turns out that every adjunction describes, in a
“syntax invariant” way, a notion of an “algebra” for an abstract “equational theory.”
The free-forgetful adjunction between pointed sets and sets induces an endofunctor {$(−)∗:Set→Set$} which adds a new disjoint point. This is called the maybe monad in computer science. (nLab, Monad)
nLab: pointed object The category of pointed objects in C is the co-slice category 1/C under the terminal object. There is an obvious forgetful functor from 1/C to C. If C has finite coproducts, this functor has a left adjoint functor which takes an object X to the coproduct 1⊔X, equipped with its obvious point (this functor underlies the “maybe monad”). This is often written X+ and called “X with a disjoint basepoint adjoined.”
The free-forgetful adjunction between monoids and sets induces an endofunctor {$T:Set→Set$} defined by {$TA:=⨆n≥0An$} giving the free monoid monad. This also goes by the name list monad or Kleene-Star? in computer science. The components of the unit {$η_A:A→TA$} give inclusions sending each element of A to the corresponding singleton list. The components of the multiplication {$μ_A:T^2A→TA$} are the concatenation functions, sending a list of lists to the corresponding list (Known as flattening in computer science). This monad can be defined in any monoidal category with coproducts that distribute over the monoidal product. (nLab, Monad)
Given any adjunction {$(F : C \to D,G : D \to C,\eta,\varepsilon)$} with associated monad T, the functor G can be factored as {$D \stackrel{\tilde G} \to C^T \stackrel{\text{forget}} \to C$}, i.e., G(Y) can be naturally endowed with a T-algebra structure for any Y in D. The adjunction is called a monadic adjunction if the first functor {$\tilde G$} yields an equivalence of categories between D and the Eilenberg–Moore category {$C^T$}. By extension, a functor {$G\colon D\to C$} is said to be monadic if it has a left adjoint {$F$} forming a monadic adjunction. For example, the free–forgetful adjunction between groups and sets is monadic, since algebras over the associated monad are groups, as was mentioned above. In general, knowing that an adjunction is monadic allows one to reconstruct objects in D out of objects in C and the T-action. (Wikipedia: Monad)
| Free construction | Forgetful functor | Notes |
| free functor | from complete semi-lattice to set | MSE: yields the powerset monad |
| free functor | from free semigroup to set | MSE: yields the list monad |
| free vector space functor {$\mathbb{k}[−]:\textbf{Set}\rightarrow\textbf{Vect}_k$} | underlying set functor {$U:\textbf{Vect}_k\rightarrow\textbf{Set}$} | Tai-Danae Bradley |
| map set to K-algebra {$X\rightarrow K[X]$} | map K-algebra to its underlying set | polynomial rings are free commutative algebras |
| turn a graph into a category by concatenating paths - free category | from category to underlying graph | Tai Danae Bradley also Varela, Kaufmann |
| Stone–Čech construction | Inclusion functor U from CHaus into Top | Stone-Čech compactification Category of compact Hausdorff spaces CHaus, category of topological spaces Top. The Axiom of Choice is used to prove the existence of the compactification. |
| functor from monoids to rings | from ring to underlying monoid | integral monoid ring construction |
| take semigroup, add identity, get monoid | from monoid to underlying semigroup | |
| take a commutative monoid, add inverses, get abelian group | take abelian group, forget inverses | Grothendieck group construction |
| abelianization: {$G\rightarrow G^{ab}=G/[G,G]$} | from abelian group to group | |
| take rng {$R$} to a ring with identity {$R\times \mathbb{Z}$} | from ring to underlying rng | |
| assigns to every ring {$R$} the pair {$(R[x],x)$} | forgetful functor {$G:\textbf{Ring}_*\rightarrow\textbf{Ring}$} | {$\textbf{Ring}_*$} pointed commutative rings with unity (pairs (A,a) where A is a ring, a ∈ A) |
| Berci Abelian groups to R-modules. | ||
| {$S\rightarrow M\times S$} with the M-action {$m\cdot <m_1,s>:= <mm_1,s>$}. And given set function {$f:S\rightarrow M$} we have a morphism of M-actions {$\phi :M\times S\rightarrow M$} given by {$<r,s>\rightarrow r\cdot f(s)$} | from monoid to underlying set | Berci Given monoid M, the category of M-actions (M-modules, M-sets) and the category Sets. |
| take integral domain (such as Z) to its field of fractions (such as Q) | forgetful functor {$\textbf{Field}\rightarrow\textbf{Dom}_m$} | category {$\textbf{Dom}_m$} of integral domains with injective morphisms |
| tensor algebra | from algebra to vector space | |
| {$F:A\rightarrow A\otimes_\mathbb{Z} S$} | {$U:R-\textrm{Mod}-S\rightarrow$}{$ R-\textrm{Mod}$} ignoring the right modules | {$(R,S)$}-bimodules and left modules |
| tensor product with {$S$} yields {$F:R-\textbf{Mod}\rightarrow$}{$ S-\textbf{Mod}$} | forgetful functor {$G:S-\textbf{Mod}\rightarrow R-\textbf{Mod}$} | given {$\rho:R\rightarrow S$} |
| forming the disjoint union space (coproduct in Top) with a point space ("adjoining a base point") {$(-)_+ := (-)\sqcup * : \textrm{Top}\rightarrow\textrm{Top}_{*}$} | forgetting base point of a topological space | relating category of topological spaces {$\textrm{Top}$} and pointed topological spaces {$\textrm{Top}_{*}$} |
| {$[x]:\mathbf{Rings}\rightarrow\mathbf{Rings}_*$} adjoins an indeterminate {$[x](R)=(R[x],x)$} | {$U:\mathbf{Rings}_*\rightarrow\mathbf{Rings}$} forgets the distinguished point {$U(A,a)=A$} | Awodey Example 9.10 |
| Sheafification functor {$\textrm{Psh}(X) \overset{j^∗}{\rightarrow} \textrm{Sh}(X)$}, {$P\mapsto j^*P$} characterized by the property that any morphism {$P\rightarrow F$} from a presheaf {$P$} to a sheaf {$F$} uniquely factorises as {$P \rightarrow j^*P \rightarrow F$} | Canonical embedding functor {$\textrm{Sh}(X) \overset{j_*}{\hookrightarrow} \textrm{Psh}(X)$} | Caramello, Lafforgue. Lecture notes. Page 4 |
| {$LC:P(X)\rightarrow D(X)$} sends a subset Y of P(X) to the lower closure of Y | includes a lower set of X as a subset of the powerset of X | P(X) is the powerset of poset X, D(X) is the downset lattice of X (all the lower sets of X) Completeness in terms of adjunctions |
Free-Forgetful adjunction that is also a Galois connection
Pick some mathematical object {$X$} that has an underlying set, for instance a group, ring, vector space, etc. For any subset {$S$} of {$X$}, let {$F(S)$} be the smallest subobject of {$X$} that contains {$S$}, i.e. the subgroup, subring or subspace generated by {$S$}. For any subobject {$U$} of {$X$}, let {$G(U)$} be the underlying set of {$U$}. (We can even take {$X$} to be a topological space, let {$F(S)$} the closure of {$S$}, and take as "subobjects of {$X$}" the closed subsets of {$X$}.) Now {$F$} and {$G$} form a monotone Galois connection between subsets of {$X$} and subobjects of {$X$}, if both are ordered by inclusion. {$F$} is the lower adjoint.  Galois connection
Galois connection
| Free functor {$F:\mathbf{Pos}\rightarrow\mathcal{C}\mathbf{Pos}$} sends {$P$} to the poset of "lower sets" {$\textrm{Low}(P)=$}{$\{Q\subseteq P | p'\leq p\in Q\Rightarrow p'\in Q\}$} | Forgetful functor {$U:\mathcal{C}\mathbf{Pos}\rightarrow\mathbf{Pos}$} forgets that a poset is cocomplete | Awodey Example 9.3. {$\mathbf{Pos}$} posets and monotone maps, {$\mathcal{C}\mathbf{Pos}$} cocomplete posets (join exists for any family of elements) and cocontinuous maps (which respect joins) |
- The insertion of groupoids Gpd into small categories Cat has both a left and a right adjoint
- Free functor from sets to commutative monoids generates bags (multisets). Adjoint functor collapses bags to sets.
- The forgetful functor takes us from RepA -> Vect A (forgets the representation, leaves the vector space). The adjoint functor is the induced module that takes us to A tensor V.
Riehl page 115: There are many instances of free constructions in mathematics. One can define the free (abelian) group on a set, the free ring on a set or on an abelian group, the free module on an abelian group, the free category on a directed graph, and so on. Sometimes there are competing notions of universal constructions: Does the free graph on a set have a single edge between every pair of vertices or none? Does the free topological space on a set have as many open sets as possible or as few? Other times there are none: For instance, there is no “free field.”
Riehl page 115: The universal property of the free vector space functor {$\mathbb{k}[−]:\textbf{Set}\rightarrow\textbf{Vect}_k$} is expressed by saying that it is left adjoint to the underlying set functor {$U:\textbf{Vect}_k\rightarrow\textbf{Set}$}: linear maps {$\mathbb{k}[S]\rightarrow\mathbf{V}$} correspond naturally to functions {$S\rightarrow U(V)$}, which specify the image of the basis vectors {$S⊂\mathbb{k}[S]$}. By the Yoneda lemma, this universal property can be used to define the action of the free vector space functor {$\mathbb{k}[−]$} on maps. The forgetful functor {$U:\textbf{Vect}_k\rightarrow\textbf{Set}$} has no right adjoint, so in this setting there are no competing notions of free construction.
With the free-forgetful adjunctions we have examples where the free construction is a tensor product and it arises as the adjoint of a forgetful map where it is given that {$\rho:\mathbf{R}\rightarrow\mathbf{S}$}, for example. (Is the latter map correct or should it be reversed?) Whereas in the tensor product - homset adjunction the morphism is with regard to the object being tensored.
Kategoriją išreiškus matrica išryškėja ryšys tarp laisvumo (freely generated) ir užmarštumo (forgetfulness functor), mat išrašus visus kategorijos slinkstis, galima "matricų daugyba" išreikšti kaip jos įvairiai komponuojasi, bet tada tenka išreikšti, kaip jos įvairiai sutampa.
nLab: Reflective subcategory is basically one that is the image of a forgetful functor. Many examples are given.
- A full subcategory i:C↪D is reflective if the inclusion functor i has a left adjoint T. The left adjoint is the reflector (free), and the right adjoint is the reflection (forgetful).
- nLab: Property vs. Structure. Whenever C is a full subcategory of D, we can say that objects of C are objects of D with some extra property. But if C is reflective in D, then we can turn this around and (by thinking of the left adjoint as a forgetful functor) think of objects of D as objects of C with (if we're lucky) some extra structure or (in any case) some extra stuff. This can always be made to work by brute force, but sometimes there is something insightful about it. For example, a metric space is a complete metric space equipped with a dense subset. Or, an integral domain is a field equipped with numerator and denominator functions.
- nLab: Reflective localization A localization of a category/of an (∞,1)-category is called reflective if its localization functor has a fully faithful right adjoint, hence if it is the reflector of a reflective subcategory/reflective sub-(∞,1)-category-inclusion. This adjoint exhibits {$L_WC$} as a reflective subcategory of C.
Forgetful without left adjoint
The forgetful functor Field → Set does not have a left adjoint. (Leinster, Example 6.3.5.) The theory of fields is unlike the theories of groups, rings, and so on, because the operation {$x \mapsto x^{-1}$} is not defined for all x (only for {$x\neq 0$}).
Forgetful without right adjoint
If a functor does not commute with colimits, then it does not have a right adjoint.
The abelianization functor does not have a right adjoint because the forgetful functor does not commute with colimits.
Free constructions
See: Forgetful functor
- Free module: the forgetful functor from {$\mathbf{Mod}(R)$} (the category of R-modules) to {$\mathbf{Set}$} has left adjoint {$\operatorname{Free} _{R}$}, with {$\displaystyle X\mapsto \operatorname {Free} _{R}(X)$}, the free R-module with basis X.
- Free group
- Free lattice
- Universal enveloping algebra
Free construction with left adjoint
| Left adjoint | Free construction | Forgetful functor | Notes |
| The universal enveloping functor U which constructs the most general algebra containing all representations of a Lie algebra | Construct a Lie algebra from an algebra by taking the Lie bracket to be the commutator. | Forget the Lie bracket and simply have an algebra without it. | Universal enveloping algebra Given an underlying field, {$\mathbf{Alg}$} is the category of algebras (unital associative algebras?), {$\mathbf{LieAlg}$} is the category of Lie algebras. |
Forgetful with left and right adjoints
Tensor - Forgetful - Hom
If we are dealing with {$R\textrm{-Mod}$} of the same ring {$R$}, then we actually have an adjoint string of functors centered on the forgetful functor {$U:R\textbf{-Mod}\rightarrow\textbf{Ab}$}. Its left adjoint is {$A\rightarrow R\otimes A$} and its right adjoint is {$A\rightarrow\textrm{Hom}_{\mathbb{Z}}(R,A)$}.
Given a group {$G$}, a (left) G-set is a pair {$(X,\rho)$} where {$X$} is a set and the action of {$G$} on {$X$} is the map {$\rho :G\times X\rightarrow G$}, where {$\rho(g,x) =g\cdot x= gx$}. Consider the category of G-sets and the category of sets. A morphism in the category of G-sets is a G-map {$f:X\rightarrow Y$} such that {$f(g\cdot x)=g\cdot f(x)$} for all {$g\in G$} and {$x\in X$}.
- We have the forgetful functor that takes us from the G-set to the set.
- The left adjoint maps S to {$G\times S$}. G acts on G as a group and acts on S trivially. (This is the tensor product adjoint.)
- Alternatively, G acts on all the functions from G to S by having G act on itself. (This is the homset adjoint.)
Forgetful with right adjoint
The left adjoint is free and the right adjoint is cofree.
Define whether the relevant concept (open) is to be understood maximally (all subsets) or minimally (almost no subsets).
| Left adjoint endows the set with the discrete (free) topology (all subsets are open). The left adjoint constructs a topological space from a set {$S$} in such a way that continuous maps from this space to another space {$T$} correspond naturally and bijectively to functions {$S\rightarrow U(T)$}. | from topological space to set | Right adjoint endows the set with the indiscrete (cofree) topology (only open sets are the whole set and the empty set). The right adjoint constructs a topological space from a set {$S$} in such a way that continuous maps from {$T$} to this space correspond naturally and bijectively to functions {$U(T)\rightarrow S$}. | ||
| {$\Delta:\textrm{Set}\rightarrow\textrm{Space}$} equips a set with the discrete topology. In consequential spaces, the discrete topology says that only eventually constant sequences converge. | {$\Gamma:\textrm{Space}\rightarrow\textrm{Set}$} is the underlying set functor. | {$\nabla:\textrm{Set}\rightarrow\textrm{Space}$} equips a set with the indiscrete topology. In consequential spaces, the indiscrete topology says that every sequence converges [uniquely] to every point. | Shulman gives these adjunctions between topos of spaces {$\textrm{Space}$} and topos of sets {$\textrm{Set}$}. A consequential space is a set equipped with, for every sequence {$(x_n)$} and point {$x_{\infty}$}, a set of “reasons why” or “ways in which” {$(x_n)$} converges to {$x_{\infty}$}. | |
| F(M) is the group obtained from monoid M by throwing in an inverse to every element. | from group to monoid | R(M) is the group which is the submonoid of M consisting of all invertible elements of M. | Leinster, page 45, example 2.13 d | |
| induction (a left Kan extension of the representation functor along the inclusion of the subgroup into the group) from a representation of a subgroup to representation of a group which extends it most generally {$\textrm{ind}^G_H:\textrm{Rep}_F(H)\rightarrow$}{$\textrm{Rep}_F(G)$}, {$\textrm{ind}^G_H:V\rightarrow$}{$ F[G]\otimes_{F[H]}V$} | restriction of representation of group to a representation of its subgroup {$\textrm{res}^G_H:\textrm{Rep}_F(G)\rightarrow$}{$\textrm{Rep}_F(H)$} | coinduction (exists for finite groups) (a right Kan extension of the representation functor along the inclusion of the subgroup into the group) {$\textrm{coind}^G_H:\textrm{Rep}_F(H)\rightarrow$}{$\textrm{Rep}_F(G)$}, {$\textrm{coind}^G_H:V\rightarrow$}{$\textrm{Hom}_{F[H]}(F[G],V)$} | ||
| extension of scalars | restriction of scalars | coextension of scalars | Frobenius reciprocity |
A left adjoint takes us from a set to a discrete graph (unconnected points); from a set to a discrete metric space (all distances are the same to others, zero to oneself); from a set to a discrete topological space (all subsets are open).
Arturo Magidin Ever wondered why the underlying set of a product of topological spaces is the product of the underlying sets, and the underlying set of a coproduct of topological spaces is also the coproduct/disjoint union of the underlying sets of the topological spaces? Why the constructions in topological spaces always seem to start by doing the corresponding thing to underlying sets, but in other categories like Group, R−Mod, only some of the constructions do that? (I know I did) It's because while in Group the underlying set functor has a left adjoint but not a right adjoint, in Top, the underlying set functor has both a left and a right adjoint (given by endowing the set with the discrete and indiscrete topologies).
Cofree coalgebra refers to a right adjoint to the forgetful functor from the category of comonoids (coalgebras with respect to the tensor product) Coalg(M) to the monoidal category M.
Algebra-left and geometry-right - this is the opposite conclusion for the case of the tensor product and homset?
- Having a right adjoint means that we have a geometry (a space) because it means that we have a global construction and thus we have a "choice framework", in other words, homogeneity.
- Having a left adjoint means that we have algebra, we have step-by-step constructions.
Inclusion. Least upper bound. Greatest lower bound.
(inclusion?) functor with both a left adjoint (from - lean on the inner structure - requalification - best post-approximation) and a right adjoint (to - lean on the external whole - best pre-approximation)
What is the difference between inclusion and forgetting? In the case of the preorders Z and R, the morphisms in R for objects of Z all carry over to Z. Whereas that is not the case when we include groups as sets.



| Left adjoint | Inclusion functor | Right adjoint | Notes |
| ceiling function {$\mathbb{R}\rightarrow \mathbb{Z}$} {$i\in \mathbb{Z} | x\leq i \wedge$}{$(\forall j\in \mathbb{Z})(x\leq j \Rightarrow i\leq j)$} | inclusion {$i:\mathbb{Z}\rightarrow\mathbb{R}$}, {$x_\mathbb{Z}\equiv x_\mathbb{R}$} | floor function {$\mathbb{R}\rightarrow \mathbb{Z}$} {$i\in \mathbb{Z} | i\leq x$}{$ \wedge (\forall j\in \mathbb{Z})(j\leq x \Rightarrow j\leq i)$} | morphism {$x\rightarrow y$} whenever {$x\leq y$}, think of counting as moving upward, thus defining "pre-approximation" and "post-approximation" |
| unfoldment of pointed graph as tree | forgetful from tree to pointed graph | unfoldment of pointed graph as tree | Varela "Principles of Biological Autonomy", pg.97 describes the left adjoint and I think the right adjoint is the same. Pointed graph morphisms (and likewise tree morphisms) map pointed vertex to pointed vertex and edge to edge going outwards |
Free construction with left adjoint, forgetful with right adjoint
| {$V$} assigns to a category to its set of connected components, and a functor to the induced mapping | {$F$} assigns to a set the discrete category on that set (only morphisms are the identity morphisms) | {$U$} assigns to a category its set of objects | {$R$} assigns to a set the indiscrete category on that set (exactly one morphism between any two objects) | Adjoint functors, Awodey, 2006. 9.6 |
Any two nonempty indiscrete categories are equivalent to each other.
Change of rings.
| induced module {$f_! M = S\otimes_R M:\text{Mod}_R \rightarrow$}{$\text{Mod}_S$} | restriction of scalars {$f^* N = N_R:\text{Mod}_S\rightarrow$}{$\text{Mod}_R $} | coinduced module {$f_* M = \operatorname{Hom}_R(S, M):\text{Mod}_R \rightarrow$}{$\text{Mod}_S$} |  Change of rings Given a ring homomorphism {$f: R \to S$}, there are three ways to change the coefficient ring of a left R-module Change of rings Given a ring homomorphism {$f: R \to S$}, there are three ways to change the coefficient ring of a left R-module |
The change of rings is related to Shapiro's lemma which can be stated for rings (in terms of Ext), and group rings (in terms of Ext), and group cohomology (in terms of the induced representation).
 Weil restriction In algebraic geometry, the term "restriction of scalars" is often used as a synonym for Weil restriction. From the standpoint of sheaves of sets:
Weil restriction In algebraic geometry, the term "restriction of scalars" is often used as a synonym for Weil restriction. From the standpoint of sheaves of sets:- Left adjoint: restriction of scalars is just a pushforward along the morphism {$\textrm{Spec}(L)\to \operatorname{Spec}(k)$}
- Right adjoint:
 fiber product of schemes. A morphism of schemes {$X → Y$} can be imagined as a family of schemes parametrized by the points of Y. Given a morphism from some other scheme Z to Y, there should be a "pullback" family of schemes over Z. This is exactly the fiber product {$X\times_Y Z \rightarrow Z$}. The proof that fiber products of schemes always do exist reduces the problem to the tensor product of commutative rings (cf.
fiber product of schemes. A morphism of schemes {$X → Y$} can be imagined as a family of schemes parametrized by the points of Y. Given a morphism from some other scheme Z to Y, there should be a "pullback" family of schemes over Z. This is exactly the fiber product {$X\times_Y Z \rightarrow Z$}. The proof that fiber products of schemes always do exist reduces the problem to the tensor product of commutative rings (cf.  gluing schemes).
gluing schemes).
 Change of rings: Relation between the extension of scalars and the restriction of scalars The extension of scalars functor is left adjoint to the restriction of scalars functor.
Change of rings: Relation between the extension of scalars and the restriction of scalars The extension of scalars functor is left adjoint to the restriction of scalars functor. Math Stack Exchange: Qiaochu Yuan on tensor-hom adjunction It's cleanest to describe the tensor-hom adjunction with three different rings instead of one, to make it as hard as possible to accidentally write down the wrong thing, so let {$A$},{$B$},{$C$} be three different rings, let {$_AM_B$} be an {$(A,B)$}-bimodule, let {$_BN_C$} be a {$(B,C)$}-bimodule, and let {$_AK_C$} be an {$(A,C)$}-bimodule. Then
{$\textrm{Hom}_{-C}( _AM_B \; \otimes_B \; _BN_C \; , \; _AK_C ) ≅ \textrm{Hom}_{B-}( _AM_B \; , \; \textrm{Hom}_{-C}( _BN_C \; , \; _AK_C))$} as {$(A,A)$}-bimodules
Qiaochu Yuan: It's an isomorphism of (A,A)-bimodules. There are two A-module structures available, one coming from acting on M (contravariantly because it's in the first slot of the hom, so it switches to a right action) and one coming from acting on K (this stays a left action), and the tensor-hom adjunction respects both.
{$\textrm{Hom}_{-A}( _AM_B \; \otimes_B \; _BN_C \; , \; _AK_C ) ≅ \textrm{Hom}_{B-}( _BN_C \; , \; \textrm{Hom}_{A-}( _AM_B \; , \; _AK_C))$} as {$(C,C)$}-bimodules.
Specialize to the case that {$A=B=C$}, then {$\textrm{Hom}_A$} has different meanings unless {$A$} is commutative and {$M$}, {$N$}, {$K$} are plain {$A$}-modules, in which case there's no need to make left/right distinctions. (Specifically, {$\textrm{Hom}_A$} means left the second, fifth, and sixth times you used it, but right the first, third, and fourth times.)
The dual version of Beck's monadicity theorem characterizes comonadic adjunctions. For example, consider the adjunction {$ - \otimes_A B : \mathbf{Mod}_A \rightleftarrows \mathbf{Mod}_B : \operatorname{forget}$} for a ring homomorphism {$A \to B$} between commutative rings. This adjunction is comonadic, by Beck's theorem, if and only if B is faithfully flat as an A-module. It thus allows to descend B-modules, equipped with a descent datum (i.e., an action of the comonad given by the adjunction) to A-modules. The resulting theory of faithfully flat descent is widely applied in algebraic geometry.
An adjoint triple {$F\dashv G\dashv H$} is Frobenius if F is naturally isomorphic to H. nLab: Frobenius functor
- K. Morita proved that the extension of scalars functor for a morphism of rings {$f:R→S$} is Frobenius iff the morphism f itself is Frobenius in the sense of (Kasch), that is: {$_R S$} is finitely generated projective and {$_S S_R≅\textrm{Hom}_R(_R S, _R R)$} as {$R−S$}-bimodules. This is in the spirit of the finite-dimensional duality coded e.g. in the notion of Frobenius algebra.
Lifting adjunctions.
Quillen adjunction A Quillen adjunction {$(F, G): C \leftrightarrows D$} between two closed model categories C and D is a special kind of adjunction between categories that induces an adjunction between the homotopy categories Ho(C) and Ho(D) via the total derived functor construction. In the total derived functor construction {$LF: Ho(C) \leftrightarrows Ho(D): RG$}, the left adjoint LF is the total left derived functor and the right adjoint RG is the total right derived functor. In the Quillen adjunction, F preserves cofibrations and trivial cofibrations. G preserves fibrations and trivial fibrations.
 Homotopy category (Quillen's definition) One first defines a weak homotopy equivalence: a continuous map is called a weak homotopy equivalence if it induces a bijection on sets of path components and a bijection on homotopy groups with arbitrary base points. Then the (true) homotopy category is defined by localizing the category of topological spaces with respect to the weak homotopy equivalences. That is, the objects are still the topological spaces, but an inverse morphism is added for each weak homotopy equivalence. This has the effect that a continuous map becomes an isomorphism in the homotopy category if and only if it is a weak homotopy equivalence. There are obvious functors from the category of topological spaces to the naive homotopy category (as defined above), and from there to the homotopy category.
Homotopy category (Quillen's definition) One first defines a weak homotopy equivalence: a continuous map is called a weak homotopy equivalence if it induces a bijection on sets of path components and a bijection on homotopy groups with arbitrary base points. Then the (true) homotopy category is defined by localizing the category of topological spaces with respect to the weak homotopy equivalences. That is, the objects are still the topological spaces, but an inverse morphism is added for each weak homotopy equivalence. This has the effect that a continuous map becomes an isomorphism in the homotopy category if and only if it is a weak homotopy equivalence. There are obvious functors from the category of topological spaces to the naive homotopy category (as defined above), and from there to the homotopy category.
- Results of J.H.C. Whitehead, in particular Whitehead's theorem and the existence of CW approximations,[4] give a more explicit description of the homotopy category. Namely, the homotopy category is equivalent to the full subcategory of the naive homotopy category that consists of CW complexes. In this respect, the homotopy category strips away much of the complexity of the category of topological spaces.
- Example: Let X be the set of natural numbers {0, 1, 2, ...} and let Y be the set {0} ∪ {1, 1/2, 1/3, ...}, both with the subspace topology from the real line. Define f: X → Y by mapping 0 to 0 and n to 1/n for positive integers n. Then f is continuous, and in fact a weak homotopy equivalence, but it is not a homotopy equivalence. Thus the naive homotopy category distinguishes spaces such as X and Y, whereas they become isomorphic in the homotopy category.
- nLab: In classical homotopy theory, a fibration p:E→B is a continuous function between topological spaces that has a certain lifting property. The most basic property is that given a point {$e∈E$} and a path {$[0,1]→B$} in B starting at {$p(e)$}, the path can be lifted to a path in E starting at e.
- Alexander Berglund, Kathryn Hess. Homotipical Algebra and Morita Theory for Corings Adjunctions of modules lifted to become adjunctions of comodules.
Consider the case of induced homomorphisms. We have continuous maps such as {$\phi:X\rightarrow Y$} between topological spaces. We can suppose that the spaces are pointed and the maps likewise so that we have {$\phi:(X,x_0)\rightarrow (Y,y_0)$}. Then we have an induction functor that takes us to the fundamental groups and their induced homomorphism {$\phi_*:\pi_1(X,x_0)\rightarrow\pi_1(Y,y_0)$}. What is the adjoint functor that takes us back?
Monad related.
Monads and adjunctions
Anirudh Sankar. Monads and algebraic structures.
Monads
- A monad is exactly the same thing as a monoidal monoid in the monoidal category {$C^C$} with composition as the monoidal product, {$G ⊗ F = G ◦ F$}. (Awodey, 10.2)
- Monads are precisely the monoids among endofunctors {$ \operatorname {End} (C)$}, which is equipped with the multiplication given by composition of endofunctors.
- An endofunctor T arises from an adjunction if and only if it is the functor part of a monad.
Duality
- Expanding (replacing Identities with L*R) and collapsing (replacing L*R with Identity).
Examples of Monads
Tom Ellis regarding monads:
- Maybe comes from the free functor into the category of pointed sets and the forgetful functor back
- [ ] comes from the free functor into the category of monoids and the forgetful functor back
- Sjoerd Visscher: Cont r comes from the adjunction of the contravariant functor Op r : Hask^op --> Hask with itself, with Op r a = a -> r.
- Vitus: State monad can be "decomposed" as the pair of adjoint functors F and G:
- data F b a = F (a,b)
- data G b a = G (b -> a)
- instance Functor (F b) where fmap f (F (a,b)) = F (f a, b)
- instance Functor (G b) where fmap f (G g) = G (f . g)
Bartosz Milewski: Unit lets us introduce the composition R ∘ L anywhere we could insert an identity functor on D; and counit lets us eliminate the composition L ∘ R, replacing it with the identity on C. That leads to some “obvious” consistency conditions, which make sure that introduction followed by elimination doesn’t change anything.
- In Haskell, unit is known as "return" (or "pure") and counit is known as "extract".
- The unit (or return) is a polymorphic function that creates a default box around a value of arbitrary type. The counit (or extract) does the reverse: it retrieves or produces a single value from a container.
The contravariant power set functor is its own right adjoint, giving {$Set(A,PB)≅Set(B,PA)$}. Note that {$hom(A,PB)=hom(A,hom(B,Ω))≅hom(A×B,Ω)=P(A×B)$} inducing a double power set monad taking a set A to {$P^2A$}. The components of the unit are the principal ultrafilter functions {$η_A:A→P^2A$} which send an element a to the set of subsets of A that contain a. The components of the multiplication μA is the inverse image function for the map {$η_{PA}:PA→P^3A$}. Which can be painfully stated as: the function taking a set of sets of sets of subsets to the set of subsets of A with the property that one of the sets of sets of subsets is the set of all sets of subsets of A that include that particular subset as an element. (nLab, Monad)
Category of adjunctions inducing a particular monad
Math Stack Exchange. Category of adjunctions inducing a particular monad.
- Every pair {$F \dashv G$} of adjoint functors {$F: \mathcal C \to \mathcal D$}, {$G: \mathcal D \to \mathcal C$} induces a monad {$\mathbb T = (T,\eta,\mu)$} on {$\mathcal C$}. Given a monad {$\mathbb T = (T,\eta,\mu)$} on {$\mathcal C$}, we define {$\operatorname{Adj}(\mathbb T)$} to be the category of adjunctions inducing {$\mathbb T$}. Its objects are adjoint pairs of functors {$F \dashv G$} between {$\mathcal C$} and some category {$\mathcal D$} such that the monad induced by the adjunction is {$\mathbb T$}, i.e. {$GF = T$}, the unit is {$\eta$}, and {$G\varepsilon F = \mu$} where {$\varepsilon$} is the counit. The morphisms between two such adjunctions {$F \dashv G$}, {$F' \dashv G'$} are functors {$H: \mathcal D \to \mathcal D'$} such that {$HF=F'$} and {$G' H = G$}.
Two extremes: (initial objects) Kleisli adjunctions and (terminal objects) Eilengberg-Moore adjunctions
- Kleisli adjunctions keep the objects the same and only change the morphisms using T. Eilenberg-Moore adjunctions map from an object X to the free T-algebra T(X).
Jeremy Gibbons: Every pair of adjoint functors gives rise to a monad. The converse holds too: every monad arises in that way. In fact, it does so in two canonical ways. One is the Kleisli construction Petr describes; the other is the Eilenberg-Moore construction. Indeed, Kleisli is the initial such way and E-M the terminal one, in a suitable category of pairs of adjoint functors. They were discovered independently in 1965. If you want the details, I highly recommend the Catsters videos.
Kleisli category
Kleisli category associated to a monad T is equivalent to the category of free T-algebras. The Kleisli category is one of two extremal solutions to the question Does every monad arise from an adjunction? The other extremal solution is the Eilenberg–Moore category.
Kleisli adjunctions
Corresponding to our intuition of what an initial object is in familiar categories like Top or Set, the Kleisli adjunction can be considered to be the smallest adjunction giving rise to the monad T. Its associated category (known as the Kleisli category) can furthermore be considered the category of “free algebras for the monad”. As we would then expect, its comparison functor is rarely an isomorphism or an equivalence of categories (although, as we will see, it is an equivalence with a certain subcategory)
Kleisli adjunctions
- The Giry Monad and Markov kernels
- C*Algebras and *-homomorphisms, Kleisli category is equivalent to C*-Algebras - completely positive unital maps
Maybe Monad
- Riehl, Category Theory in Context: Example 5.3.2. The Kleisli adjunction for the maybe monad is identified in Example 5.2.10(i) as the adjunction between the category of sets and the category of sets and partially-defined functions: {$\textrm{Set}\dashv\textrm{Set}∂$}.
- The maybe monad is the operation X↦X∐*. The idea here is that a function X⟶Y in its Kleisli category is in the original category a function of the form X⟶Y∐* so either returns indeed a value in Y or else returns the unique element of the unit type/terminal object *. This is then naturally interpreted as “no value returned”, hence as indicating a “failure in computation”.
- nLab: Maybe Monad
- Nikolai Durov, New Approach to Arakelov Geometry The algebraic structure of the would be “field with one element” is regarded as being the maybe monad, hence modules over {$F_1$} are defined to be monad-algebras over the maybe monad, hence pointed sets.
Emily Riehl. A categorical view of computational effects.
Categorical probability theory
- Arthur Parzygnat
- Videos
- Thoughts on math and science
- nLab: Giry monad
- nLab: Monads of probability measures and valuations
- nLab: Probability theory
- David Corfield. What is this category enchrined in?
Adjoint modality
Adjoint cylinder, Adjoint modality
- nLab: Adjoint modality An adjunction between idempotent monad and idempotent comonad (nLab: adjoint monads).
- Equivalently, an adjoint cylinder is an adjoint triple such that the outer two adjoints are full and faithful functors.
- Is meant to express specifically a duality between opposites.
- nLab: adjoint monad Every adjoint triple {$F^∗⊣F_∗⊣F^!$} induces an adjoint pair {$F^∗F_∗⊣F_∗F^!$}. The endofunctor {$F^∗F_∗$} is underlying a monad induced by the adjunction {$F^∗⊣F_∗$} and {$F_∗F^!$} is underlying a comonad induced by the adjuntion {$F_∗⊣F^!$}. This pair of a monad and a comonad are adjoint.
- nLab: Hegel's Science of Logic with reference to adjunctions.
- Aufhebung Lawvere inspired by Hegel
Other.
Adjoint triple
- If one of the two adjoint pairs induced from an adjoint triple involving identities, then the other exhibits an adjoint cylinder / unity of opposites.
- An affine morphism is an adjoint triple of functors in which the middle term is conservative. For example, any affine morphism of schemes induce an affine triples of functors among the categories of quasicoherent modules.
- An adjoint triple of functors among {$A_\infty$}- or triangulated functors with certain additional structure is called spherical . See e.g. (Anno). The main examples come from Serre functors in a Calabi-Yau category context.
- An adjoint triple {$F \dashv G \dashv H$} is called an ambidextrous adjunction (or sometimes ambijunction, for short) if the left adjoint F and the right adjoint H of G are equivalent {$F \simeq H$}.
Long adjoint strings
nLab: Adjoint string Let [n] denote the totally ordered (n+1)-element set, regarded as a category. The morphisms are the relations {$\geq$}. Functors are order preserving maps. For each positive integer n, we have n+1 order-preserving injections from [n-1] to [n], and n order-preserving surjections from [n] to [n-1]. Thus there are 2n+1 functors in all. Regarded as functors, these injections and surjections interleave to form an adjoint chain of length 2n + 1. These categories, functors, and adjunctions form the simplex category regarded as a locally posetal 2-category; see below.
- Let C be a category with a terminal object but no initial object. Then there are functors {$\delta_i: [n+1,C] \to [n,C]$}, {$0\leq i \leq n$}, {$\sigma_i: [n,C] \to [n+1,C]$}, {$0\leq i \leq n$} such that {$\delta_0 \dashv \sigma_0 \dashv \cdots \dashv \delta_n \dashv \sigma_n$} is a maximal string of adjoint functors (all but {$\sigma_n$} are obtained by applying {$[−,C][-, C]$} to the simplex category example, and {$\sigma_n$} exploits the presence of the terminal object of C).
- Generalizing the simplex category example: if P is a lax idempotent monad with unit {$u: 1 \to P$} and multiplication {$m: P P \to P$} (so that {$m \dashv u P$}), then there is an adjoint string {$P^{n-1} m \dashv P^{n-1} u P \dashv P^{n-2}m P \dashv \ldots \dashv m P^{n-1} \dashv u P^n$} of length {$2 n + 1$}, back and forth between {$P^{n+1}$} and {$P^n$}. The example of [n] and [n+1] above is based on the fact that the simplex category {$\Delta$}, regarded as a locally posetal bicategory, is the walking lax idempotent monoid.
Given an ambidextrous adjunction, {$F \dashv G$} and {$G \dashv F$}, we of course get an infinite adjoint string {$\ldots \dashv F \dashv G \dashv F \dashv \ldots$} of period 2.
More examples of adjunctions
- Algebraic number satisfying polynomial. Constructing algebraic number from algebraic number by field operations. Are these two issues related with an adjunction?
- Solvability - chain related to adjunctions.
- Adjunction example: initial collapsing terminal 2.1.9
- Relational algebra by way of adjunctions, paper, video
- Database queries: Selections, projections, equijoins.
- Elias Zafiris. Category-theoretic analysis of the notion of complementarity for quantum systems. (See:
 Complementarity as with position and momentum, or time and energy.) Adjunction between the category of quantum event algebras and the category of presheaves on Boolean event algebras. Establishes local or partial structural congruences between the quantum and Boolean kinds of event structure. If we consider a Boolean modeling functor {$M:B → L$} there exists precisely one corresponding uniquely defined, up to isomorphism, colimit-preserving functor {$\hat{M}:\textrm{Sets}^{B^{op}}\rightarrow \mathfrak{L}$} such that the following diagram commutes... The functor {$\hat{M}:=\textbf{L}$} is the left adjoint of the categorical adjunction between the categories {$\textrm{Sets}^{B^{op}}$} and {$\textbf{L}:\textrm{Sets}^{B^{op}}\rightarrow \mathfrak{L}$} whilst the right adjoint functor {$\textbf{R}:\mathfrak{L}\rightarrow\textrm{Sets}^{B^{op}}$} is physically interpreted as the Boolean realization functor of {$\mathfrak{L}$} in terms of variable local probing frames, functioning as natural contexts for measurement of observables. The existence of the functorial relations designate the fact that a quantum event algebra {$\mathfrak{L}$} in {$L$} can be expressed in terms of structured multitudes of interlocking local Boolean frames capable of carrying all the information encoded in the former.
Complementarity as with position and momentum, or time and energy.) Adjunction between the category of quantum event algebras and the category of presheaves on Boolean event algebras. Establishes local or partial structural congruences between the quantum and Boolean kinds of event structure. If we consider a Boolean modeling functor {$M:B → L$} there exists precisely one corresponding uniquely defined, up to isomorphism, colimit-preserving functor {$\hat{M}:\textrm{Sets}^{B^{op}}\rightarrow \mathfrak{L}$} such that the following diagram commutes... The functor {$\hat{M}:=\textbf{L}$} is the left adjoint of the categorical adjunction between the categories {$\textrm{Sets}^{B^{op}}$} and {$\textbf{L}:\textrm{Sets}^{B^{op}}\rightarrow \mathfrak{L}$} whilst the right adjoint functor {$\textbf{R}:\mathfrak{L}\rightarrow\textrm{Sets}^{B^{op}}$} is physically interpreted as the Boolean realization functor of {$\mathfrak{L}$} in terms of variable local probing frames, functioning as natural contexts for measurement of observables. The existence of the functorial relations designate the fact that a quantum event algebra {$\mathfrak{L}$} in {$L$} can be expressed in terms of structured multitudes of interlocking local Boolean frames capable of carrying all the information encoded in the former.
| Geometric realization | Nerve operation Singularization | nLab: nerve and realization |
Geometric (topological) realization makes the abstract simplicial set concrete.
nLab: Geometry of Physics: Categories and Toposes: Example 1.61 There is a reflective subcategory-inclusion (Def. 1.60)
{$$ \textrm{Set} \overset {\overset{\pi_0}{\longleftarrow}} {\underset {\hookrightarrow}{\bot}} \textrm{Grp} $$}
of the category of sets (Example 1.2) into the category Grpd (Example 1.16) of small groupoids (Example 1.10) where
- the right adjoint full subcategory inclusion (Def. 1.19) sends a set S to the groupoid with set of objects being S, and the only morphisms being the identity morphisms on these objects (also called the discrete groupoid on S, but this terminology is ambiguous)
- the left adjoint reflector sends a small groupoid {$𝒢\mathcal{G}$} to its set of connected components, namely to the set of equivalence classes under the equivalence relation on the set of objects, which regards two objects as equivalent, if there is any morphism between them.
HoTT Book page 60: Every topological space X has a fundamental ∞-groupoid whose k-morphisms are the k-dimensional paths in X. The weakness of the ∞-groupoid corresponds directly to the fact that paths form a group only up to homotopy, with the (k + 1)-paths serving as the homotopies between the k-paths. Moreover, the view of a space as an ∞-groupoid preserves enough aspects of the space to do homotopy theory: the fundamental ∞-groupoid construction is adjoint to the geometric realization of an ∞-groupoid as a space, and this adjunction preserves homotopy theory (this is called the homotopy hypothesis/theorem, because whether it is a hypothesis or theorem depends on how you define ∞-groupoid). For example, you can easily define the fundamental group of an ∞-groupoid, and if you calculate the fundamental group of the fundamental ∞-groupoid of a space, it will agree with the classical definition of fundamental group of that space. Because of this correspondence, homotopy theory and higher-dimensional category theory are intimately related.
- The adjunction between the singular simplicial set functor and geometric realization, or the adjunction between the nerve functor and the fundamental category functor. Omar Antolín-Camarena, nlab: Nerve and Realization
- Example 3.1.7 For the inclusion ∆ → Cat where [n] is mapped to the category given by the poset in the natural way by adding identities, we get a right adjoint which is commonly known as the nerve functor, and a left adjoint which maps a simplicial set to its homotopy category. Axel Sarlin. The étale fundamental group, étale homotopy and anabelian geometry.
Is the fundamental group functor a left adjoint?
nLab: Grothendieck construction has a left adjoint and a right adjoint.
- (shape modality ⊣ flat modality ⊣ sharp modality) {$\esh \dashv \flat \dashv \sharp $}
- discrete object, codiscrete object, concrete object
- points-to-pieces transform
- structures in cohesion
- dR-shape modality⊣ dR-flat modality ʃ dR⊣♭ dR
- differential cohesion (reduction modality ⊣\dashv infinitesimal shape modality ⊣\dashv infinitesimal flat modality) {$\Re \dashv \Im \dashv \& $}
- reduced object, coreduced object, formally smooth object
- formally étale map
- structures in differential cohesion
- graded differential cohesion
- fermionic modality⊣ bosonic modality ⊣ rheonomy modality (⇉⊣⇝⊣Rh)
A canonical exact sequence relating open immersion, close immersion and six functor formalism.
- See also: Closed immersions and abelian sheaves
- and the chapter Sheaves of Modules about the six functor formalism.
Paul Garrett. Adjoints, naturality, exactness, small Yoneda lemma The proof that left adjoints are right-exact, and that right adjoints are left-exact, uses a small incarnation of Yoneda’s Lemma, and illustrates the importance of naturality of isomorphisms.
Natural examples of sequences of adjoint functors Many important examples.
Left/right exact functor "in nature" which is not a right/left adjoint
Notes
Adjunctions
- Ko Aoki. The sheaves-spectrum adjunction. The smashing spectrum functor is right adjoint to the spectral sheaves functor; it in particular gives an external definition using neither objects, ideals, nor localizations. This sheaves-spectrum adjunction informally means that the smashing spectrum gives the best approximation of a given ∞-category by ∞-categories of sheaves.
- Egbert Rijke: Here's a fun thing you can do with the natural numbers ordered by divisibility: Show that the Fibonacci sequence has a left adjoint.
- Adjunction models the relationship between God and Human, going back and forth, the levels of understanding. Why are there different kinds of adjunctions?
- Fausk, Hu, May. Isomorphisms Between Left and Right Adjoints
- Is there a sense in which the isomorphic adjoints are like the zero vector spaces in exact sequences?
- nLab: Generalisation as an adjunction
- http://www.j-paine.org/generalisation.html
- The examples are two-dimensional points (members of R 2). Generalisation is least-squares fitting, as above. The concept is a line giving the best least-squares fit to the points.
- Compact-open topology If X is locally compact, then X × − {\displaystyle X\times -} from the category of topological spaces always has a right adjoint H o m ( X , − ) {\displaystyle Hom(X,-)}. This adjoint coincides with the compact-open topology and may be used to uniquely define it. The modification of the definition for compactly generated spaces may be viewed as taking the adjoint of the product in the category of compactly generated spaces instead of the category of topological spaces, which ensures that the right adjoint always exists.
- Adjunction relates two worlds, two modules and one can be set to zero, and division of everything structures what happens. Adjunction is a shift between perspectives. Is it one of 12 circumstances?
- Adjunction? Language is more expressive then language is less decidable (less determinable in the proof theoretic sense).
- Example: Presburger arithmetic
- Example: Simplicial homology - easy to formulate but lots to calculate. Singular homology - subtle to formulate, much less to calculate.
- https://ncatlab.org/nlab/show/being According to (Hegel 12) pure being is the opposite of nothing whose unity is pure becoming. According to the formalization of this proposed by (Lawvere 91), this is described by the adjoint modality {$(\emptyset \dashv \ast)$} of the idempotent monad constant on a terminal object {$\ast$} and its left adjoint {$\emptyset$}.
Tensor Hom adjunction
- (AxB->C) left adjoint to (A->(B->C))
- general function left adjoint to values on elements
- free construction left adjoint to forgetful
- Conjugacy ? the values of adjunction
- Lifting a path is like inverting a functor. How is that related to adjunctions? Adjunction is conditional inversion.
Enveloping algebra (important for adjunctions) is related to Hochschild cohomology which is a special case of the functor Ext.
- {$\operatorname{Hom}_{A^e}(A,M)$} (where {$A^e:=A\otimes_k A^{op}$} is the enveloping algebra of A and A is considered an A-bimodule via the usual left and right multiplication)
- Classify adjunctions, metaphors = classify trivialities
- Adjunction: Sigma and Pi in dependent type theory.
- Induction and recursion are adjoints.
- Consider the move from opposites coexist to all things the same as an example of the forgetful functor forgetting the opposites. Are opposites given by {$i^2=-1$}? Can such forgetting ground all of the exact sequences? And does the forgetting mean that they can be understood as adjoint strings?
- Galois adjunctions
- Rushabh Mehta. Galois Covers and the Fundamental Group.
- Compression and decompression (interpolation) as an adjunction.
- Knowledge of why (the essence) lets you compress. But how also lets us compress. Does What let us compress?
- https://ncatlab.org/nlab/show/Functorial+Semantics+of+Algebraic+Theories
- Lawvere's thesis is all about adjunctions.
- Reprints in Theory and Applications of Categories
- https://math.stackexchange.com/questions/467640/categorical-interpretation-of-quantification
- https://topos.site/blog/2023/07/a-nuclear-adjunction-between-poly-and-dir/
- In classifying adjunctions, consider what are the constraints on the categories so that the adjunctions are well defined. For example, what must hold for categories to have all limits or have all colimits? Note that these will be two separate constraints in the case of an adjoint string of two adjunctions.
- Question and answer - two functors in an adjunction. Question goes from the known world (category) (mind that knows) to the unknown world (mind that does not know) and the answer goes in the other direction. So we start with a question and we end with an answer.
- Terrence Tao. Trying to understand the Galois correspondence.
- Kantorovich Lifting: Representation as Fibred Adjunction. Goes between V-SPred and V-Cat.
- John Baez's forgetful functor on representations of Clifford algebras (in talking about symmetric spaces). The adjoint functor is defined by essential fiber, the category of ways that an object b in B can arise from applying a functor {$p:E \rightarrow B$} to some object in {$E$}.
- Free means "no filter" (as in "everything has no filter") whereas forgetting is obstructing.
- Constant (in quantification) brings to mind the representations of the nullsome (and the trivialities).
- Lawvere. Adjointness in Foundations.
- The tensor algebra is the free associative algebra generated by V. The tensor algebra defines a functor T from the category of vector spaces to the category of associative algebras, which is left adjoint to the forgetful functor going in the opposite direction. Spin Lecture 1
https://ncatlab.org/nlab/show/ambidextrous+adjunction
https://mathoverflow.net/questions/13832/analogies-between-analogies reply regarding adjunctions
- Ivan Ivanovich. How Hegel ended up in String Theory
- Combinatorial QFT on Graphs. Get adjoint to coboundary operator. Combining them gives the graph Laplacian.
Polanyi's tacit and explicit. Forgetful functor yields tacit, free construction yields explicit.