• View
• Edit
• History
• Print

Upcoming Videos

Here is a list of upcoming videos that I'm working on.

Coming Soon

Here I order the videos in groups, in terms of the order in which I intend to release the top video in each group.

Mathematics of Divisions of Everything

• John: ...go through the videos we recorded...
• Andrius: Quantum Symmetries Bridge Physics and Metaphysics

Landscape of Truth and Value

• Investigation of the landscape of truth
• Conversations on Relationships with Truth, Deepest Values and investigations

Wondrous Wisdom Concepts

• Narration
• Three Minds Essay at the Theory Translator
• Doubts and Counterquestions
• Expectations and Emotional Responses
• Values and ... ?
• Research: Verbalization and Good Will Exercises
• Meaning of Life - parts 5, 6
• Qualities of Signs
• Qualities of Signs and the Meaning of Life

Physics

• John: Quantum probability theory 2
• Thomas: Quantum Field Theory Personally
• Thomas: General Relativity Personally
• Andrius: Combinatorial Alternative to Wave Functions
• John: Symmetries and contexts with examples: Unitary, Lagrangian, Hamiltonian.
• SU(2) - Andrius and John
• Time and Space as Representations of Decision-Making
• Quantum narrative: Combinatorics of moments of orthogonal Sheffer polynomials
• Classification of orthogonal Sheffer polynomials

Wondrous Wisdom Research

24 Keys to Math

All Upcoming

Here is a list of all of the videos I currently envision.

Wondrous Wisdom

Overview of Wondrous Wisdom

• I present what I know of the language of wondrous wisdom with a series of videos based on slides which I talk about.

Wondrous Wisdom Research Updates

• From the big picture to the role of wisdom
• Relating the counterquestions, the wisdom exercises and the flow of experience
• Investigating meaningful experiences
• Possibly...
  • God Doesn't Have To Be Good (Gospel of John)
  • God Doesn't Have To Be Good (My Life Experiences)

Wondrous Wisdom Future Research

• Analyze God and Other Ultimates

4 Reservations

Counterquestions

• Examples: Doubts and Counterquestions
• Exercises: Examples of Doubts (from every day life)
• Exercises: Examples of Doubts (from literature)
• Exercises: Examples of Doubts (from Scriptures)
• Answers to Exercises
• 8 Counterquestions: Framework for Intelligence
• Engaging the Violent
• Exercises: Examples of Structures
• Answers to Exercises
• Truths of the Heart and of the World

Four reservations

• Operating principles for Needs
• Counterquestions for Doubts
• Directions of the good for Expectations
• Investigations for Values

Application: Peacemaking for Russia and Ukraine

• My letter to the Russian government.
• An Epistemological Portrait of Russian Federation President Vladimir Putin.

Math for God: From Binomial Theorem to Bott Periodicity

Binomial Theorem: Gateway to God in Math

• Pascal's triangle. Calculate, what is the probability that in a family with 3 children there are 2 girls and 1 boy?
• Calculate, for example, (1 + 0.01)^n, which is to say, what happens when you have small growth, as with an interest rate of 1% ?
• The geometry of squares and cubes (in 3 dimensions but also in higher dimensions), how they grow, (x+h)^n, where h is small.
• Derivatives of powers of x, which we can also understand in terms of slopes.
• Prove the binomial theorem, "n choose k", in different ways, counting subsets of sets. One way is to use mathematical induction.
• Relate the binomial theorem to the Euler characteristic and Betti numbers.
• Consider the Gaussian binomial coefficient, how it counts subspaces of vector spaces over a finite field F_q. And we can imagine what happens when q goes to 1.
• Relate the binomial theorem to the binomial distribution and enter the world of probability and statistics but also orthogonal polynomials.
• Discuss the Grassmannian and how it relates to Bott periodicity.

Math tutorials

Q-analogue of Binomial Coefficients

• I want to make a video about the q analogue of the binomial coefficients and how we get the mythical "field with one element" when we take the limit q goes to 1. That is important for modeling choice when we have only one choice to choose from. I think this is relevant for modeling God.

Structure of Finite Fields

• Understand the structure of finite fields of cardinality {$q^n$} and then consider what happens when we take the limit {$q\rightarrow 1$}. This should give insight into modeling {$F_1$}.

Calculating representations of Clifford algebras as relevant for Bott periodicity

Raudys Hierarchy of Statistical Methods

Understand the Raudys hierarchy and how it may express the divisions of everything.

• (1) the Euclidean distance classifier;
• (2) the standard Fisher linear discriminant function (DF);
• (3) the Fisher linear DF with pseudo-inversion of the covariance matrix;
• (4) regularized linear discriminant analysis;
• (5) the generalized Fisher DF;
• (6) the minimum empirical error classifier;
• (7) the maximum margin classifier.

Threesome for Participation

Mathematical Beauty Awakens the Imagination

I made a picture in a talk I gave in Lithuanian http://www.ms.lt/sodas/Mintys/MatematikosGrožisŽadinaVaizduotę

I gave this as an example of mathematical beauty where our mind can break out of the limits of what we can see. I compare that with the visual beauty of the Mandelbrot set, which exemplifies Christopher Alexander's 15 properties of life, including three related to one (good shape), all (local symmetry of background), many (positive, concave space).

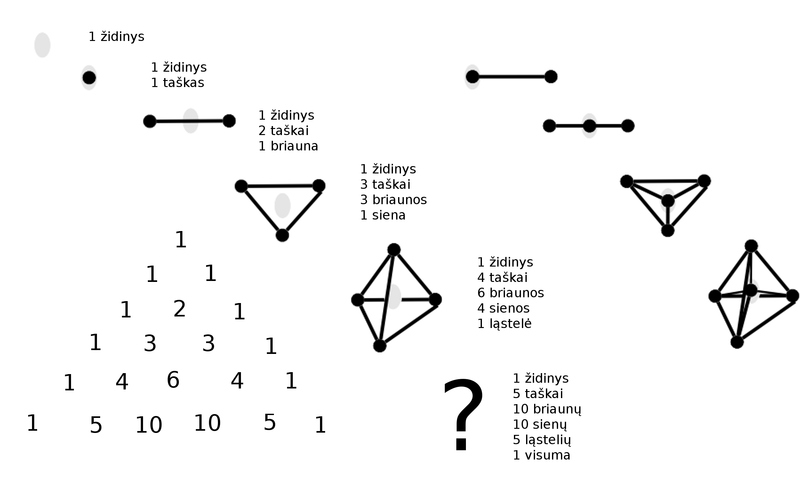
Animating the 4-simplex. Visualizing 4 dimensions with 5 points.

• I wonder how best to animate the 4-simplex. I know some Python. I should learn the basics of Manim.
• I draw a tetrahedron (four points - four dimensions) and introduce a fifth point at the center (which becomes a fifth dimension when I wiggle it around). Using Pascal's triangle we see how the row for an edge 1 2 1

becomes the row for a triangle 1 3 3 1 (one center, three vertices, three edges, one face) becomes the row for a tetrahedron 1 4 6 4 1 (one center, four vertices, six edges, four faces, one volume) becomes the row for a 4-simplex 1 5 10 10 5 1 (one center, five vertices, ten edges, ten faces, five volumes, 1 4-dimensional-cell)

Foursome for Knowledge

I will make many short videos about the Yoneda Lemma and how it functions as a knowledge switch relating the four levels of knowledge: Whether, What, How, Why.

Yoneda Lemma and the four levels of knowledge

• General idea as a knowledge switch
• Natural Isomorphism
• Interpreting the Natural Isomorphism
• Example: Cayley's Theorem
• More examples
• The foursome: overview
• Examples of the foursome
• The foursome as a building block
• The foursome: exercises
• The foursome: discussion of answers
• In terms of Kan extensions
• Isbell duality
• Coends and ends?

Norman Anderson's Information Integration Theory

• Investigate how averaging (by the unconscious) is teased apart as addition and multiplication (by the conscious).

Yates Index Set Theorem

• Explain what this says about the foursome of levels of knowledge: Whether, What, How, Why.

Classifying adjunctions

The Fundamental Theorem of Covering Spaces

• This is part of my study of adjunctions with the goal of classifying adjunctions. This particular adjunction is an equivalence. I have been studying algebraic topology at the New York Category Theory Meetups and you are welcome to join us.

Fivesome for Decision Making

Time and Space as Representations of Decision-Making

Orthogonal Sheffer polynomials

• Classification of orthogonal Sheffer polynomials
• Combinatorics of Hermite polynomials

Minkowski space and Moebius transformations

The Fivesome, Quadraticity and the Eccentricity of the Conics

Sevensome for Logic

Eight dualities

• Investigate the kinds of dualities.

Shu-Hong Zhu's Thesis

• Present as an example of the sevensome. And relate to linear fractional transformations.

Six Conceptions

Symmetric functions of the eigenvalues of a matrix

• Seeking a relation to the six representations, for example, a connection with Hopf algebras.

{$K^{-1}K=I$} and nonexistence of an involution

• Set this up as a problem where the nonexistence of an adjunction indicates the nonexistence of a combinatorial interpretation for an involution.

Grothendieck's six functor formalism

24 Keys to Math

24 Ways of Figuring Things Out in Math

• Surface structure and deep structure Completed.
• Groups of ways of figuring things out (4, 4, 3, 4, 6, 3)
• Talk on visualizations as the source of paradox
• Overviewing the entire system
• Investigating further...

I want to make videos about the 24 ways of figuring things out in mathematics.

Visualization as Restructuring and thus a Source of Logical Paradox

24 Keys to Various Disciplines

• 24 Ways of Figuring Things Out in Biology
• Buckminster Fuller's 24 Ways of Figuring Things Out

Threesome for Participation

• Zig Zag Lemma
• Mathematical Beauty Awakens the Imagination

Math for Divisions of Everything

• Andrius and John: 2x2 matrices and rotations
• Andrius Kulikauskas: SU(2) (junior level)
• John Harland: Quaternions. (junior level)
• Francis Howard: SU(2) (senior level)

6 Conceptions

• Classifying adjunctions
• Grothendieck's six functor formalism

Sevensome for Logic

• Investigate the kinds of dualities.

Language of Wisdom Study Group

• 24 Ways of Figuring Things Out in Biology
• Jere's understanding of atoms and molecules
• Ironija Holokausto kaltininkus pažinojusiųjų atsiminimuose
• Three Languages: Narration, Verbalization, Argumentation
• Foursome and Equation of Life

Investigation of Geometry

• Mathematical frameworks for geometry

Landscape of Truth and Value

• Conversations on Relationships with Truth, Deepest Values and investigations with Samuel Hutchens
• Investigation of the landscape of truth
• Conversations on Relationships with Truth. With Bill Pahl, Thomas Gajdosik, John Harland, Jon Brett, Kirby Urner, Silvijus Pokštas