• View
• Edit
• History
• Print

Orthogonal polynomials

Orthogonal polynomials are inescapable in quantum mechanics. They are the nit and grit of calculations for solving the Schroedinger equation. They have rational terms that beg to be interpreted combinatorially. This line of exploration is very natural to me because of my Ph.D. thesis in algebraic combinatorics.

Interpretation of these polynomial terms spills the guts of quantum mechanics. It yields clues as to how space and time relate to energy, how they get constructed from cells, what is the role of measurement, and overall, how the wave function works.

The harmonic oscillator: Hermite polynomials.

The harmonic oscillator seems to be a paradigmatic example to understand. The solutions involve the Hermite polynomials as key factors. I became curious, what could these polynomials actually mean, combinatorially and physically?

It turns out that there are two variants of Hermite polynomials, those used by physicists and those used by probabilists. Below is a nice interpretation of the probabilist version.

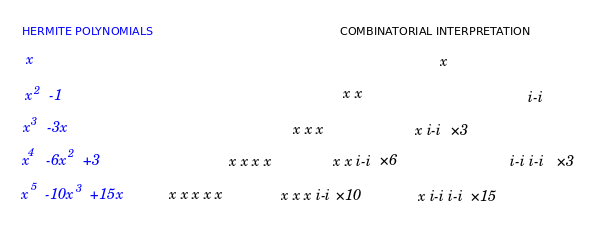
Mathematically, the probabilist Hermite polynomials {$\textrm{He}_n$} are generating (in a sense, "counting") the involutions on {$n$} letters, which is to say, those permutations of {$n$} letters which are their own inverses. These are precisely the permutations that consist of one-cycles and two-cycles. Each one-cycle is assigned weight {$x$} and each two-cycle is assigned weight {$-1$}. For example, there are four involutions on the letters {$1, 2, 3$}, namely the identity {$()$}, which gets weight {$x^3$}, and the three two-cycles {$(1 2)$}, {$(1 3)$}, {$(2 3)$}, which each get weight {$-x$}. Their combined weight is {$\textrm{He}_3=x^3-3x$}.

In physics, the above combinatorics expresses Wick's theorem for fermions. With some imagination and some hindsight, we can interpret {$\textrm{He}_n$} as enumerating the possibilities for a set of {$n$} places in space. The energy rises with the number of places. An empty place is given weight {$x$}. The energy is a sum of contributions from configurations, and the highest power contribution (making for greatest variation) is when each place is empty. A place may be nonempty if it is linked with some other place, in which case they each get weight {$i$} or each get weight {$j=-i$}, contributing a total weight of {$i^2=j^2=-1$}. In working with {$i$} it is crucial to remember that it is never a single number but always stands for identical twins, the conjugates {$i$} and {$j$}, which are alike in all their properties except that they are not each other. We have no basis to distinguish them except that one is not the other. I imagine the contribution of {$i$} indicates momentum and simply time. It is as if a place is nonempty if time is hopping back and forth there. The sense is that a place can be nonempty only if it is occupied in an ambiguous way, so that {$i + (-i)$} = 0 at each nonempty space and yet the total weight is {$-1$} for the pair of nonempty spaces. Note also that we are distinguishing the possibility of "objects" (one-cycles) and "relationships" (two-cycles) which is so important for category theory, notably the two perspectives of the Yoneda lemma. Overall, my point is that a successful interpretation of the polynomial can, should and will carry physical intuition that is simple, deep, rich and basic.

Interpreting the derivative

Taking the derivative of the function {$e^{x^2}$} involves using the chain rule. If we continue taking the derivative, then we are also using the product rule. The function {$e^{x^2}$} persists but get multiplied by a Hermite polynomial. The chain rule yields a new factor of {$2x$}, which is the weight of a square. The product rule has us differentiate the Hermite polynomial, which means eliminating one of the x's, or rather, filling it in with an i, and also filling in the new cell with an i, yielding a weight of -1. Thus although we do add a new cell, but it is filled and also we fill an existing cell. This is the effect of the derivative operator, which is the momentum.

The positions commute in that we don't have to keep track of their order. But we have to keep track of the momentums because their order matters.

The hydrogen atom: Laguerre polynomials

The idea that the weight {$x$} indicates an empty space suggests itself in the intepretation of the Laguerre polynomials, which arise in solving the Schroedinger equation for the hydrogen atom. In combinatorics, the Laguerre polynomials are related to the rook polynomials, which count the ways of placing rooks on a chessboard so that no two rooks attack each other. More abstractly, we can count partially defined permutation matrices, which is to say, matrices of {$0$}s and {$1$}s with at most one {$1$} in each row and each column.

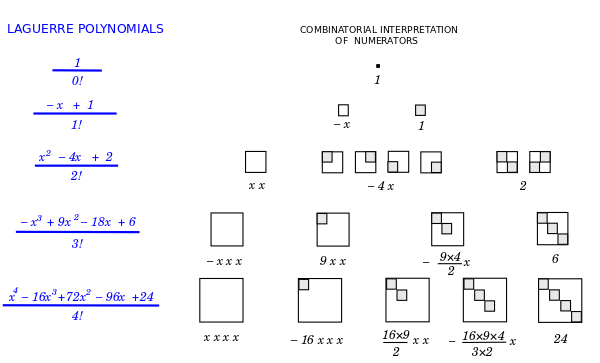
The solution to Schroedinger's equation for the hydrogen atom is given by the radial wave function {$\rho^{l+1}e^{–\rho}\nu(\rho)$} where {$p$} is the distance of the electron from the proton. The asymptotic behavior, when {$\rho\rightarrow\infty$}, so that the electron is free of the proton, is given by the factor {$\rho^{l+1}e^{–\rho}\nu(\rho)$}. The remaining, nonasymptotic factor, {$\nu(\rho)$}, is an associated Laguerre polynomial, multiplied by some normalization constant. This factor accounts for the peculiarities when the electron is close to the proton. The closer the electron, the higher the energy, and the more possibilities.

The associated Laguerre polynomials {$L_n^{(\alpha)}$} are simply a generalization of the Laguerre polynomials {$L_n$}. They are based on rectangular {$n\times(n + \alpha)$} chessboards rather than square {$n\times n$} chessboards but seem to be otherwise the same.

Evidently, the matrices (the boards) and their squares are describing the possible relations between the proton and the electron. Note that the denominator {$n!$} asserts that, say, the order of the {$n$} columns is irrelevant whereas the order of the {$n$} rows is relevant. This suggests, for example, that the proton is taken as given, at the center of mass, and so its possible relations (its rows) are defined absolutely, well ordered, whereas the electron's relations (its columns), are defined relatively, thus not ordered.

We see from the interpretations that the energy is given by the size of the matrices. The factor {$\nu(\rho)=L_{n-l-1}^{2l+1}(2p)$} is indexed by {$0\leq l \leq n$}. This means that, say, the height of the matrix is {$n-l-1$} and the width is {$l+1$}. Gaining or losing energy involves increasing or decreasing the width of the matrix, which is to say, the electron's possible relations

The relation between the electron and proton may be completely undefined, as with a

Exclusivity principle

The rook polynomials in the solution to the hydrogen atom bring to mind the principle of exclusivity which is important for fermions such as the proton and electron.

Exclusivity seems to be a central concept in defining orthogonal polynomials. Kim and Zeng have a marvelous combinatorial formula for the linearization coefficients of the general Sheffer polynomials, which specializes to many of the orthogonal polynomials that come up in solutions of the Schroedinger equation. These linearization coefficients have to do with products of the polynomials and I have yet to understand how they relate to the much simpler questions that I am exploring. However, their formula is based on derangements, which are permutations without fixed points, and thus may perhaps be considered as models of exclusivity.

Infinite well: Chebyshev polynomials

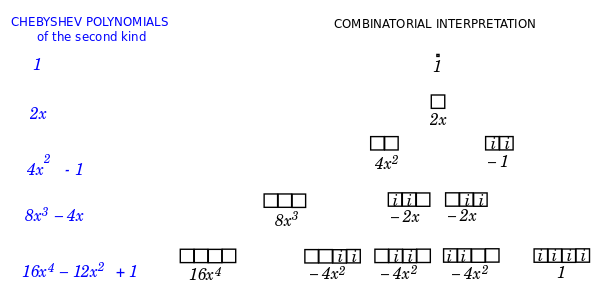
Empty cell has weight 2x

Note that in the Chebyshev polynomial the empty cell is given weight 2x. This is a recurring theme. The physicist Hermite polynomials likewise give the empty cell the weight 2x. And the model of the hydrogen atom expresses the associated Laguerre polynomial in terms of the input {$2\rho$}.

The z-axis component: associated Legendre function

I have an interpretation of the terms of the Legendre polynomial. It is given by the ways of taking paths on a square grid from (0,0) to (n,n) where the possible steps are East (weight x), North (weight 1), and East-North-East (weight -1). In other words, a step north may be thought of as having a particle with weight 1, and a step east-north-east may have, instead, two particles, each with weight i.

This generating function is related to approximating pi with a fraction.

I will try to find interpretations for the associated Legendre functions.

Energy and space. Measurement as the violation of least action

The weight {$x$} is a measurement of space, that is, of an empty place. Such a measurement takes energy. It is a violation of the principle of least action. The energy expresses that violation. Furthermore, measuring empty space, where nothing happens, indicates the perspective of an observer's choice framework, the simplexes.

Other polynomials to consider

• The angular equation (and spherical harmonics): Associated Legendre functions.
• Infinite spherical well (Griffiths, 4.40). Spherical Bessel functions and spherical Neumann functions.

Stephen Wolfram's List of Exact Solutions

Here is a helpful footnote from Stephen Wolfram's book A New Kind of Science, which is available online for free.

Some notable cases where closed-form analytical results have been found in terms of standard mathematical functions include:

• quadratic equations (~2000 BC) (Sqrt)
• cubic, quartic equations (1530s) ({$x^{1/n}$})
• 2-body problem (1687) (Cos)
• catenary (1690) (Cosh)
• brachistochrone (1696) (Sin)
• spinning top (1849 1888 1888) (JacobiSN, WeierstrassP, hyperelliptic functions)
• quintic equations (1858) (EllipticTheta)
• half-plane diffraction (1896) (FresnelC)
• Mie scattering (1908) (BesselJ, BesselY, LegendreP)
• Einstein equations (Schwarzschild (1916), Reissner–Nordström (1916), Kerr (1963) solutions) (rational and trigonometric functions)
• quantum hydrogen atom and harmonic oscillator (1927) (LaguerreL, HermiteH)
• 2D Ising model (1944) (Sinh, EllipticK)
• various Feynman diagrams (1960s-1980s) (PolyLog)
• KdV equation (1967) (Sech etc.)
• Toda lattice (1967) (Sech)
• six-vertex spin model (1967) (Sinh integrals)
• Calogero–Moser model (1971) (Hypergeometric1F1)
• Yang–Mills instantons (1975) (rational functions)
• hard-hexagon spin model (1979) (EllipticTheta)
• additive cellular automata (1984) (MultiplicativeOrder)
• Seiberg–Witten supersymmetric theory (1994) (Hypergeometric2F1).

When problems are originally stated as differential equations, results in terms of integrals ("quadrature") are sometimes considered exact solutions—as occasionally are convergent series. When one exact solution is found, there often end up being a whole family—with much investigation going into the symmetries that relate them. It is notable that when many of the examples above were discovered they were at first expected to have broad significance in their fields. But the fact that few actually did can be seen as further evidence of how narrow the scope of computational reducibility usually is. Notable examples of systems that have been much investigated, but where no exact solutions have been found include the 3D Ising model, quantum anharmonic oscillator and quantum helium atom. - Stephen Wolfram, A New Kind of Science, Notes to Chapter 12, Section 6.

Stephen Wolfram champions a computational approach, which favors form over content. He bets that there are not that many forms available and that by running through all possibilities we will stumble across the right one. But I rather invest to penetrate the meaning of what we already know Nature to be saying. I am combinatorially interpreting the exact solutions of the Schroedinger equation to discover clues to unlock the mystery of more general situations.

For my research notes, see: Research.OrthogonalPolynomials, Research.QuantumPhysicsResearch

As usual, many of my observations are speculative. You may wonder, What does Andrius know about quantum physics?