• View
• Edit
• History
• Print

Feynman diagrams

I have been studying quantum physics in order to gain intuition on Lie theory. In making sense of the Schroedinger equation, I explored the combinatorics of orthogonal polynomials, which manifested two kinds of causality that I am familiar with from the division of everything into five perspectives for decision-making: Every effect has had its cause but not every cause has had its effect.

I am now studying quantum field theory in order to understand these ideas in the most realistic setting where we have creation and annihilation of particles and we are working in relativistic space time.

How can I efficiently master the fundamentals of quantum field theory that are relevant for my research into orthogonal polynomials?

It seems that the heart of quantum field theory is actually not that complicated. There are these layers of daunting mathematics but they are basically irrelevant to the heart of the matter, which is combinatorial.

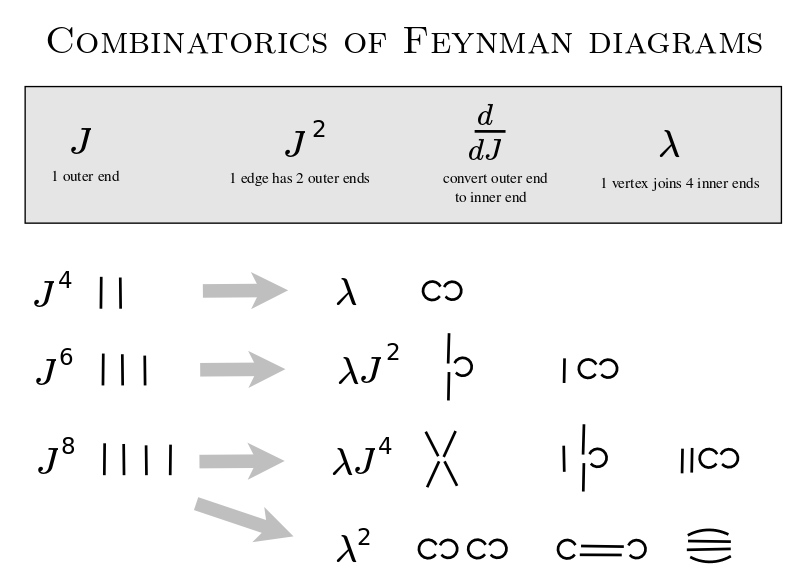
Quantum field theory is primarily (more than 50%) about understanding and interpreting the combinatorics of Feynman diagrams (or whatever equivalent formulation). This is much the same as saying that quantum mechanics is primarily about understanding and interpreting the Schroedinger equation.

Combinatorially, the Feynman diagrams let us count the ways that we can start with {$n$} incoming particles, have {$k$} interactions take place, and end up with {$n$} outgoing particles.

Physically, the Feynman diagrams serve to portray and calculate what could happen starting with a set of incoming particles and ending with a set of outgoing particles. Which is to say, in between there could be all manner of interactions, which includes particles being created and annihilated.

The diagram consists of vertices (where interactions take place) and edges that connect them (by which particles travel). The edges can be external (physically real - incoming and outgoing) or internal (between vertices, thus virtual). In the internal edges, you aren't bound by the speed of light.

All of the potential energy manifests itself at the vertices. A vertex can involve at most 4 edges if we are in 4 dimensional space time. The potential energy is thus local and is based on the particles involved. The kinetic energy is all in the edges by which a particle moves from one interaction to another interaction. So the diagrams are constructing space-time from local interactions. Lorentz invariance comes because the interactions are local.

If an edge is directed, then the particle is charged, and it can be interpreted as moving in one direction with one charge or in the reverse direction with the opposite charge. If an edge is nondirected, then it has no charge. So this is a way of defining charge.

I see how Wick's theorem relates to Hermite polynomials. I imagine that Feynman diagrams will relate somehow to Zeng saplings.

Pedagogically, it has similar challenges as quantum mechanics. One approach is to get into the nitty gritty of generating Feynman diagrams and calculating with them (in the spirit of Griffiths). But that can leave one completely lacking any overall understanding. An alternative, which Zee takes in his book "Quantum Field Theory in a Nutshell", is to present you with the pedagogically relevant math equations (a baby equation, a child equation, and the real thing) and argue that the heart of the matter is in the simplistic baby equation, and then leave it to you to figure out the Feynman diagram rules, what they mathematically must be. What seems to work for me is to approach the subject from different teachers with their different angles.

I have to learn how to do the calculations and generate the diagrams. But basically, as Zee explains, in the baby version, it's a matter of having one infinite series of differential operators e^{lambda (d/dJ)^4} act upon another infinite series of powers in a variable e^{J^2}. You look at a specific term in the output, fixing the power of lambda and the power of J, which has one differential operator acting on one power. What keeps that from being trivial is that the differential operator is in the fourth power (because you have four external legs, as when you have two incoming and two outgoing), and also that it acts on a "mother function" e^{J^2}. So that allows for some combinatorics that results from the product rule and the chain rule interacting over four applications. Each diagram in the term will have the same number of vertices (interactions), as specified by the power of lambda.

In the resulting combinatorics, we end up with contractions

Here we have the exact same "mother function" as we do for the Hermite polynomials and the quantum harmonic oscillator.

Feynman propagator

My research notes: Research.FeynmanDiagrams