Math 4 Wisdom. "Mathematics for Wisdom" by Andrius Kulikauskas.

Andrius proposes
building AI tools for our
Theory Translator

Jere updates us
on developments in
TimberFish Ecotechnology

Andrius proposes
the CIMC fund publication
of his Allegory

Welcome to Math 4 Wisdom. Read the transcript and watch the video.


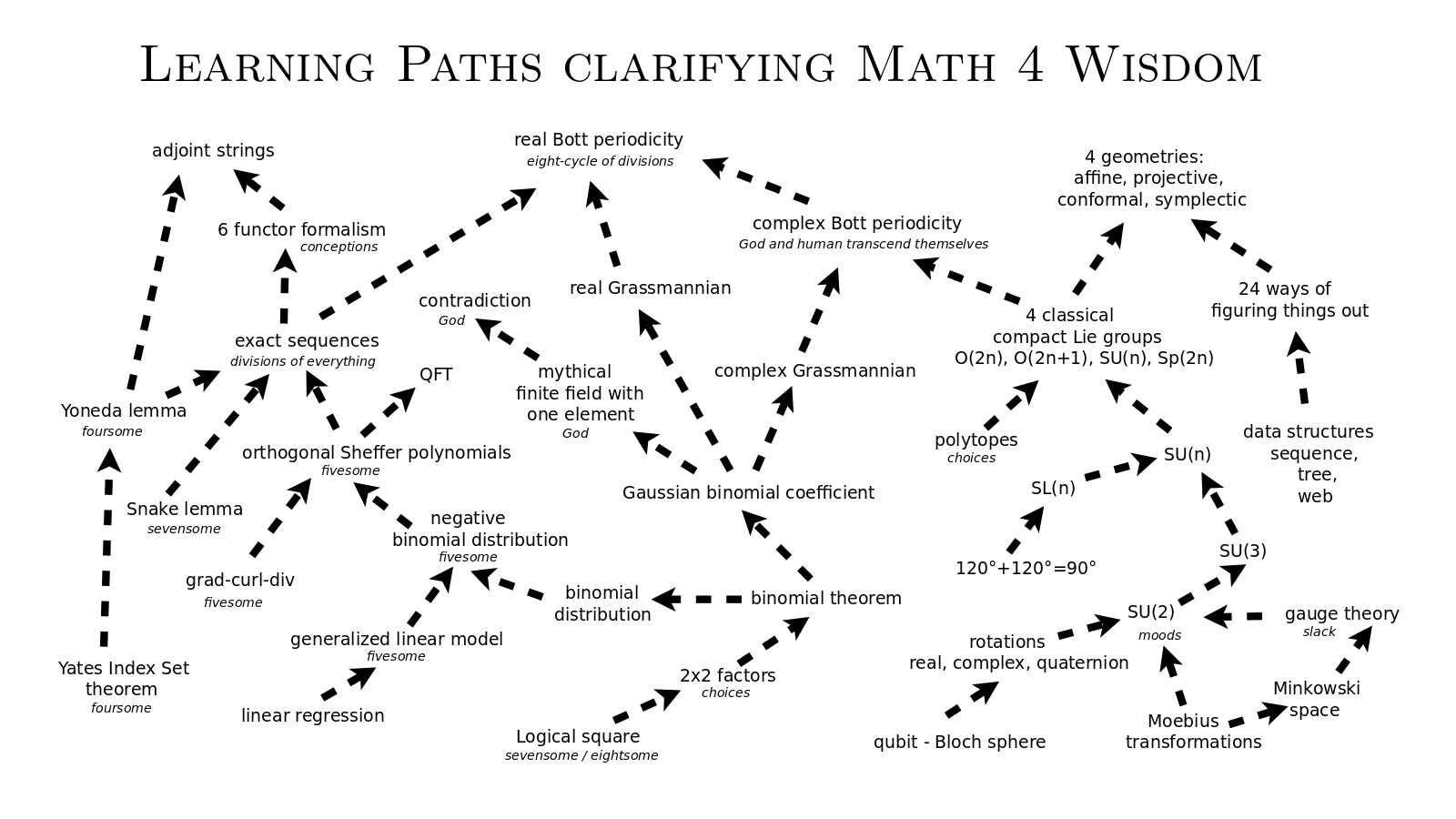Andrius Kulikauskas hosts Math 4 Wisdom	Learning Paths in Math 4 Wisdom

Math 4 Wisdom is an investigatory community for absolute truth led by Andrius Kulikauskas. That's me!

In particular, our community supports my efforts to develop Wondrous Wisdom, a language of wisdom based on the cognitive frameworks that I have been documenting since 1982. This includes showing where they arise in advanced mathematics, including algebraic topology (Bott periodicity, chain complexes), category theory (Yoneda lemma, adjunctions), complex geometry (Möbius transformations), combinatorics (binomial theorem), automata theory (Chomsky hierarchy) and quantum physics (orthogonal Sheffer polynomials).

Research.Notes . . . September 04, 2025, at 06:57 PM by AndriusKulikauskas:
Research.LivingWithThreeMinds . . . August 31, 2025, at 12:44 PM by AndriusKulikauskas:
Exposition.Introduction . . . August 31, 2025, at 10:39 AM by AndriusKulikauskas:

We present our ongoing research at the Math 4 Wisdom YouTube channel.

Please join us! Our social hub is the Math 4 Wisdom Email Group. You can subscribe or unsubscribe yourself. Here is our archive. Thank you, Marcus Petz, Jere Northrop, Daniel Friedman and all for your thoughtful letters. My letters include:

Welcome to the Math 4 Wisdom email group!, How best to participate at Math 4 Wisdom?, 2025.07.30 My priorities for investigation, collaboration and outreach

Andrius Kulikauskas and colleagues

I, Andrius Kulikauskas, offer a context of Wondrous Wisdom through my own ongoing investigations into absolute truth.

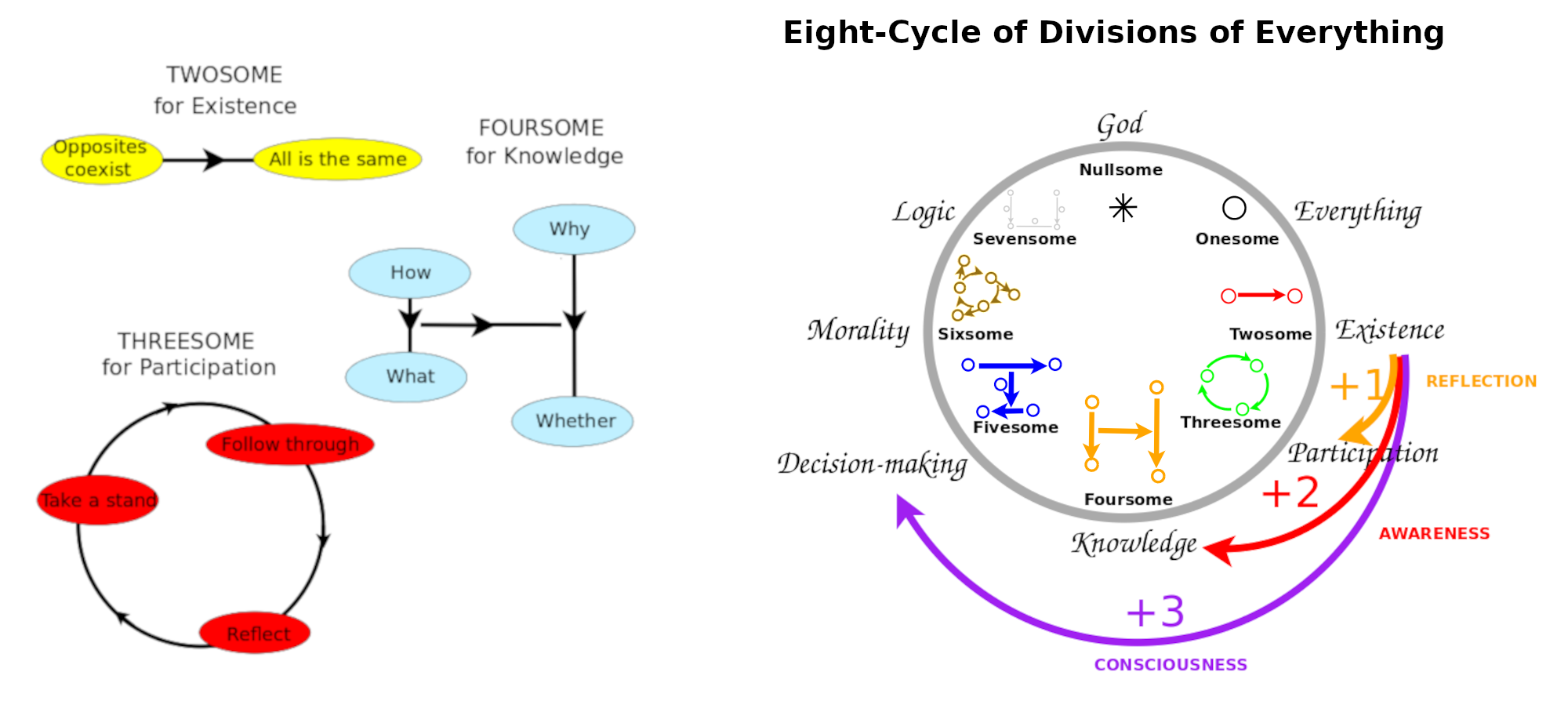
Language of Wisdom is a bottom-up documentation of the cognitive frameworks of the perspectives by which we experience life, especially abstractly, as divorced from direct experience, and from accumulated assumptions, considering the limits of consciousness itself, and thereby, the possibilities of the conscious and the unconscious.
Logos: God as Theory is a top-down interpretation of these frameworks in terms of God's investigations (whether, what, how, why there is God? respectively, as God, I, You, Other) and human's investigations (how to live as God? namely, through eternal life, wisdom, good will, God's will).
Math 4 Wisdom is my work to identify those frameworks where they appear in the language of advanced mathematics. I present these findings in terms of '''three minds - the unconscious (which knows the answers), the conscious (which asks the questions) and consciousness (which relates them with investigations) - that can be observed in psychology, neuroscience, consciousness studies and related disiciplines.
Landscape of Truth is my view on our Math 4 Wisdom community as a social experiment. We are applying knowledge usefully, as in peacemaking. We are learning to investigate alongside each other, leveraging the diversity in our relationships with truth, living in consciousness.
Personal Growth is my concern to grow forever, learn forever, live forever as a person and as a leader.
God's Investigations is my endeavor to recognize, engage and support God as an investigator.

I work at this wiki (in English) and also at www.ms.lt (in Lithuanian).

Wondrous Andrius

Thank you! for supporting Math4Wisdom through Patreon

Sign up here!
Thank you to Daniel Friedman, John Harland, Bill Pahl and 3 anonymous supporters!