Introduction E9F5FC

Questions FFFFC0

• View
• Edit
• History
• Print

狭义相对论

读物

• Split-complex number
• Why does E=mc2 and why should we care?

Formulas

My approach is to focus on the problem, which follows from the Pythagorean theorem, that the speed of light is different for different observers. And then various resolutions are possible to this problem. But I focus on velocity.

The speed of light is constant in a frame.

• Consider a clock where light bounces up and down, and let the clock be at rest in one frame, which is moving with velocity {$v$} in terms of another frame. For simplicity, we can consider a single bounce down.
• Then the speed of light as measured in the first frame appears to contract as observed from the second frame.

The speed of light {$c$} is the same constant in all frames.

• In each frame {$f$}, the speed of light is given by {$\frac{x_f}{t_f}$}.
• Thus it seems that time contracts (if the distance does not) or that space contracts (if the time does not).

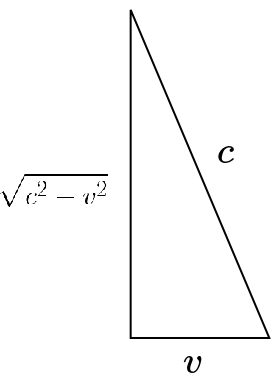
{$x=tc$} and {$x'=t'\sqrt{c^2-v^2}$}

If {$x=x'$}, then {$tc=t'\sqrt{c^2-v^2}$} and thus {$t=t'\sqrt{1-\frac{v^2}{c^2}}$}. Light clock is perpendicular to motion.

If {$t=t'$}, then {$\frac{x}{c}= \frac{x'}{\sqrt{c^2-v^2}}$} and thus {$x=\frac{x'}{\sqrt{1-\frac{v^2}{c^2}}}$}. Comparing rods is parallel to motion.

The Lorentz transformation is:

{$t' = \gamma (t-\frac{vx}{c^2})$}

{$x' = \gamma (x-vt)$}

where {$\gamma = \frac{1}{\sqrt{1-\frac{v^2}{c^2}}}$}. Note that {$v\leq c$} implies that {$\gamma \geq 1$}.

Define {$\tau = ct$}, {$\tau'=ct'$}, {$\beta=\frac{v}{c}$}. Let {$\theta$} be the angle in my right triangle which is between the leg {$\sqrt{c^2-v^2}$} and the hypotenuse {$c$}. We can have a similar right triangle with hypotenuse {$1$} and its legs will have lengths {$\alpha=\frac{1}{\gamma}$} and {$\beta$}. Thus we have {$\textrm{sec}\;\theta=\frac{1}{\alpha}=\gamma$} and {$\textrm{tan}\;\theta=\frac{\beta}{\alpha}=\beta\gamma$}. Thus we can write the Lorentz transformation as:

{$\tau' = \tau\;\textrm{sec}\;\theta - x\;\textrm{tan}\;\theta$}

{$x' = x\;\textrm{sec}\;\theta - \tau\;\textrm{tan}\;\theta$}

Furthermore we have

{$$\gamma = \textrm{sec}\;\theta = \frac{c}{\sqrt{c^2-v^2}} = \frac{c+v+c-v}{2\sqrt{c^2-v^2}}=\frac{1}{2}(\sqrt{\frac{c+v}{c-v}}+\sqrt{\frac{c-v}{c+v}})$$}

{$$\beta\gamma = \textrm{tan}\;\theta = \frac{v}{\sqrt{c^2-v^2}} = \frac{c+v-c+v}{2\sqrt{c^2-v^2}}=\frac{1}{2}(\sqrt{\frac{c+v}{c-v}}-\sqrt{\frac{c-v}{c+v}})$$}

We can simplify the mathematics by setting the "inferred speed of light" {$c^2 - v^2 = 1$}. (Rather than setting {$c=1$}). Then by the formulas above we get {$\textrm{sec}\;\theta = \gamma = c$} and {$\textrm{tan}\;\theta = \beta\gamma = v$}. The Lorentz transformation becomes remarkably simple:

{$\tau' = \tau c - x v$}

{$x' = x c - \tau v$}

The transformation matrix is:

{$\begin{pmatrix} c & -v \\ -v & c \end{pmatrix} \begin{pmatrix} \tau \\ x \end{pmatrix} = \begin{pmatrix} \tau' \\ x' \end{pmatrix} $}

The eigenvalues and eigenvectors are:

{$\begin{pmatrix} c & -v \\ -v & c \end{pmatrix} \begin{pmatrix} a \\ a \end{pmatrix} = (c - v) \begin{pmatrix} a \\ a \end{pmatrix} $}

{$\begin{pmatrix} c & -v \\ -v & c \end{pmatrix} \begin{pmatrix} a \\ -a \end{pmatrix} = (c + v) \begin{pmatrix} a \\ -a \end{pmatrix} $}

{$\begin{pmatrix} c & -v \\ -v & c \end{pmatrix} = \frac{1}{2a^2} \begin{pmatrix} a & -a \\ a & a \end{pmatrix} \begin{pmatrix} c-v & 0 \\ 0 & c+v \end{pmatrix} \begin{pmatrix} a & a \\ -a & a \end{pmatrix} $}

Thus one eigenvector has {$x=\tau=ct$} with eigenvalue {$c - v$}. The other eigenvector has {$x=-\tau=-ct$} with eigenvalue {$c+v$}.

This matrix represents a split complex number {$c - jv$}.

It can be thought of as a hyperbolic rotation by a hyperbolic angle.

{$\begin{pmatrix} \textrm{cosh}\;a & \textrm{sinh}\;a \\ \textrm{sinh}\;a & \textrm{cosh}\;a \end{pmatrix}$}

Note that the determinant of the matrix is {$\textrm{cosh}^2\;a - \textrm{sinh}^2\;a = 1$}, just as {$c^2 - v^2 = 1$}.

We can write {$\textrm{cosh}\;(-a) = c = \textrm{sec}\;\theta$} and {$\textrm{sinh}\;(-a) = -v = \textrm{tan}\;\theta$}. They are different interpretations of the same triangle.

{$e^a = \textrm{sec}\;\theta - \textrm{tan}\;\theta = c + v$}

{$e^{-a} = \textrm{sec}\;\theta + \textrm{tan}\;\theta = c - v$}

These are the two eigenvalues of the transformation matrix.

These eigenvalues can be intepreted in terms of the following tangent half-angle formula:

{$\textrm{tan}\;\frac{1}{2}\theta \pm \frac{\pi}{2} = \textrm{sec}\;\theta \pm \textrm{tan}\;\theta$}

{$\tau' = c\tau - vx$}

{$x' = -v\tau + cx$}

{$\tau'^2 = (c\tau - vx)^2 = c^2\tau^2 - 2cv\tau x + v^2x^2$}

{$x'^2 = (-v\tau + cx)^2 = v^2\tau^2 - 2cv\tau x + c^2x^2$}

{$-\tau'^2 + x^2 = (v^2-c^2)\tau^2 + (c^2-v^2)x^2 = -\tau^2 + x^2$}

{$\sqrt{v^2-c^2}\tau' = i c\tau - i vx$}

{$\sqrt{c^2-v^2}x' = -v\tau + cx$}

{$\begin{pmatrix} x' \\ i\tau' \end{pmatrix} = \begin{pmatrix} c & -iv \\ -iv & c \end{pmatrix} \begin{pmatrix} x \\ i\tau \end{pmatrix} $}

{$s^2 = x_0^2 - x_1^2$}

{$s^2 = (ct)^2 - x_1^2$}

{$s^2 = (ct)^2(1 - \frac{x_1^2}{c^2t^2})$}

{$s = ct\sqrt{1 - \frac{v^2}{c^2}}$}

{$\frac{s}{c} = t\sqrt{1 - \frac{v^2}{c^2}} = \tau$}

Proper time. In the case of a particle, it refers to a clock traveling with that particle.

{$P = m(\frac{x_0}{\tau}, \frac{x_1}{\tau}, ... )$}

{$x_0 = ct$}

{$p_0=\frac{mct}{\tau}$}, {$p_1=\frac{mx_1}{\tau} = \frac{mx_1}{t}\frac{t}{\tau}$}

{$\frac{t}{\tau}=\frac{1}{\sqrt{1 - \frac{v^2}{c^2}}}$}

{$p_0=\frac{mc}{\sqrt{1 - \frac{v^2}{c^2}}}$}, {$p_1=\frac{mv}{\sqrt{1 - \frac{v^2}{c^2}}}$}

{$(1+x)^n=1 + nx + \cdots$}

{$(1-\frac{v^2}{c^2})^{-\frac{1}{2}} = 1 + \frac{v^2}{2c^2} + \cdots $}

{$p_1 = mv + \frac{mv^3}{2c^2}$}, {$p_0 = mc + \frac{1}{2c}mv^2 + \cdots $}

{$cp_0 = mc^2 + \frac{1}{2}mv^2 + \cdots $}

{$E = mc^2$}

{$x_0^2 - x_1^2$}

{$p_0^2 - p_1^2$}

{$(mc\gamma )^2 - (mv\gamma )^2$}

{$m^2\gamma^2(c^2 - v^2)$}

{$m^2\gamma^2 c^2(1 - \frac{v^2}{c^2}) = m^2c^2$}

{$p_0^2 - p_1^2$}

{$(\frac{E}{c})^2 - p^2 = m^2c^2$}

{$E^2 = c^2p^2 + m^2c^4$}

{$E^2 = m^2c^4$}

{$E=mc^2$}

Causality

Simultaneity. Same place: {$x=0$}, same time: {$t=0$}.

{$t=0, x'=0$}

{$t'=(t-\frac{u}{c^2}x$}\gamma = 0 because {$t=0, x=0$}

{$\frac{u}{c}=\beta$}

{$x_1' = \frac{x_1 - \beta x_0}{\sqrt{1-\beta^2}}$} and {$x_0' = \frac{x_0 - \beta x_1}{\sqrt{1-\beta^2}}$}

{$s^2 = x_0^2 - x_1^2$}

{$x_0^2 = (ct)^2$}

{${x_0'}^2 - {x_1'}^2 = (x_0 - \beta x_1)^2\gamma - (x_1 - \beta x_0)^2 \gamma $}

{$= \frac{x_0^2 - 2\beta x_0x_1 + \beta^2 x_1^2 - (x_1^2 - 2\beta x_0x_1 + \beta^2 x_0^2)}{1 - \beta^2}$}

{$= \frac{x_0^2 + \beta^2x_1^2 - x_1^2 - \beta^2x_0}{1 - \beta^2} = x_0^2(1-\beta^2)$}

Notes

https://www.wolframphysics.org/technical-introduction/potential-relation-to-physics/motion-and-special-relativity/

• Road to Reality: (Moebius) transformations send circles to circles on the Riemann sphere. This remarkable fact has a significance for relativity theory that we shall come to in §18.5 (and it has deep relevance to spinor and twistor theory; see §22.8, §24.7, §§33.2,4)
• Albert Einstein. Relativity: The Special and the General Theory
• Quantum mechanics deals with mass behavior whereas relativity with idealized center of mass. Four layers of parsing relate them.
• In special relativity, think of distance squared over time as surface area per time, the difference beween the surface areas of two spheres, one expanding with velocity v, and the other with velocity c.
• My approach to special relativity lets me work in units in my own frame.
• Special relativity - causal connection - are they time like connected.
• Do the quaternions relate to Minkowski space (-,+,+,+) ? with one dimension plus three dimensions ?
• Local - special relativity, global - general relativity
• Penrose, Rindler. Spinors and Space-Time: Volume 1, Two-Spinor Calculus and Relativistic Fields

From a dream: I imagined that I was entering a spherical world full of structures, and that my perspective upon those structures was a hyperbolic geometry, expressing the Lorentz contraction, thus special relativity.

In physics, the identity component of the Lorentz group acts on the celestial sphere in the same way that the Möbius group acts on the Riemann sphere. In fact, these two groups are isomorphic. An observer who accelerates to relativistic velocities will see the pattern of constellations as seen near the Earth continuously transform according to infinitesimal Möbius transformations. This observation is often taken as the starting point of twistor theory.

https://physics.stackexchange.com/questions/566963/what-is-the-exact-meaning-of-lorentz-invariance-for-a-quantum-scalar-field

• Louis Kauffman. Special Relativity and a Calculus of Distinctions.

Minkowski space. Time {$-t^2$} has us step out (thus reversing direction), space {$x^2+y^2+z^2$} has us step in.