Math 4 Wisdom. "Mathematics for Wisdom" by Andrius Kulikauskas.

See: Research Priorities

Not Current Priorities

Wondrous Wisdom

I want to understand the science of love as a framework for that unfolding from the Indefinite to the Definite to the Imagineable to the Unimagineable.
- I am making a diagram of the most basic concepts.
  - I want to relate to that diagram the concepts of the meaning of life, which I refer to in my presentation Divine Understanding and Human Imagination
- I am trying to understand God's perspective.

I am improving my understanding of the meaning of life.
I want to understand the dynamics of human experience in terms of three languages: argumentation (how things come to matter), verbalization (how meaning arises) and narration (how events happen).
- Study the truths of the heart and the world to understand how meaning arises.
- Study chess games for how issues come to matter.
- Study the mathematical concepts in the Mathematical Companion to understand how meaning arises.
I want to relate the houses of knowledge (ways of figuring things out) in various disciplines related to life, including biology, chemistry, microbiology, ecotechnology, mathematics, as well as for various personalities.

Mathematical physics

Work out a physical interpretation of the combinatorics of orthogonal Sheffer polynomials for a new understanding of Schroedinger's equation with the hope of applying that further to quantum field theory.
- Write up and publish a video of my current understanding: A Combinatorial Alternative to the Wave Function
- Divide up the understanding I seek into elements and related problems, organize them and note for each element and each problem the progress, if any, that I have made.
  - Diagram the big picture of what is involved in this understanding.
- Understand the Kim Zeng involution.
- Understand the polynomial coefficients
  - Reinterpret the trees in terms of particle clocks.
  - Interpret {$A(t), u(t)$} and {$u'(t)$} in terms of the combinatorics. Figure out how to calculate these series.
- Consider what momentum {$\hat p=-i\hbar\frac{\partial}{\partial x}$} and expected momentum would mean combinatorially in the case of the quantum harmonic oscillator
- Understand the quantum narrative in terms of the combinatorics of the moments.
  - Given the recurrence formula, write out the definitions of the five polynomials.
    - Understand how to interpret the quantum narrative for the moments, the polynomial coefficients and the probability distributions.
    - Compare the notation that Chihara, Kim and Zeng, and I use for the Meixner polynomials, Charlier polynomials, Laguerre polynomials, Hermite polynomials and Meixner-Pollaczek polynomials.
    - Understand how to define the Laguerre polynomials.
    - Understand how to define the Kravchuk polynomials.
  - Given the polynomials, understand the moments in terms of combinatorial objects.
    - I want to understand if the Meixner polynomials relate at all with the ordered Bell numbers.
  - Relate the combinatorial objects which express the moments with Zeng's formula for the moments in terms of permutations.
    - I want to compare the expression of the moments of the Meixner polynomials in terms of permutations (by Kim and Zeng) with the expression for the moments of the orthogonal Sheffer polynomials, and also with the generating function for the moments of the Meixner polynomials.
  - I want to understand how the moments transform as we go from the Meixner to the Charlier, Laguerre, Hermite and Meixner-Pollaczek polynomials.
- Give a combinatorial interpretation of the definite integral of the square of the wave function (the product {$P_n(x)P_n(x)$}) from {$x$} to {$x+\delta$}.
- Write out Meixner's proof of the classification of the orthogonal Sheffer polynomials.
  - I am trying to understand how to calculate a nice and meaningful expression for {$A(t)$} as I do for {$u(t)$}.
- I want to understand how the associated distributions likewise transform as we proceed from the Meixner to the other polynomials.
  - I want to understand how these moments ground the distribution associated with the Meixner polynomials.
  - I want to understand how to use complex integration to get the distribution for the Laguerre polynomials.
  - I want to understand how to get the distribution of the Meixner-Pollaczek polynomials.

Geometry

Overview the geometrical concepts, branches presented in the Math Companion
- Consider how they fit within the entirety of mathematics
Identify key perspectives on geometrical thinking
Compare those key perspectives across eight layers of geometry

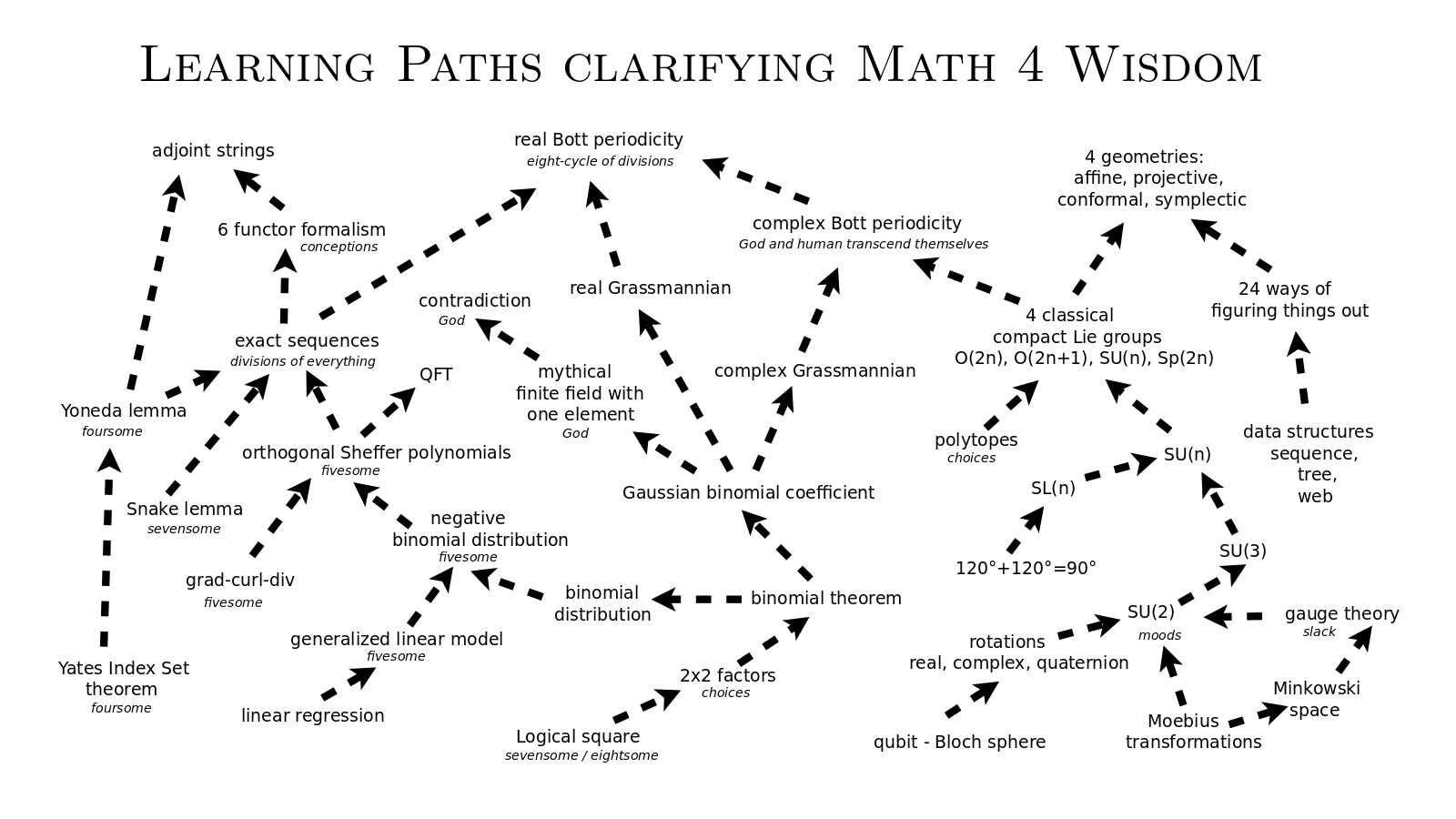
Organize my learning paths

Start by mapping out my interests related to geometry
Map out all of my interests in math
- List the relevant math structures for me to understand and why
- Make a diagram relating these structures
- Add links to related math that would help me understand
Improve my existing map of branches of mathematics
- Consider how my map of interests relates to the map of all of math

Peacemaking

Sketch an epistemological portrait of Vladimir Putin.

From before

My key wiki pages for learning, studying, investigating math

Connections in math with the cognitive frameworks of Wondrous Wisdom (up to 2021)
- Coincidences which suggest potential connections
Math big picture My efforts to understand all of math
- The purpose of math Understand what distinguishes math from other languages and disciplines.
- Math discovery Uncover the system by which things are figured out in mathematics.
- Map of math Show how math unfolds, how its various branches and concepts arise.
  - Math Companion Organize concepts from The Princeton Companion to Mathematics.
- Basic math Formulate and appreciate the most basic mathematical principles.
- Implicit math Understand the metaphysical roots of math as a cognitive language that we experience.
- Math dimensions Distinguish and investigate the many dimensions of math, such as beauty, history, education, insight, learning, humanity.
My research interests in math from 2020, from 2019 and from 2018.
Math I want to learn
- Topics, readings, videos from 2021
- Questions from 2020