- MathNotebook
- MathConcepts
- StudyMath
- Geometry
- Logic
- Bott periodicity
- CategoryTheory
- FieldWithOneElement
- MathDiscovery
- Math Connections
Epistemology
- m a t h 4 w i s d o m - g m a i l
- +370 607 27 665
- My work is in the Public Domain for all to share freely.
- 读物 书 影片 维基百科
Introduction E9F5FC
Questions FFFFC0
Software
See: Math Concepts, Math Intuition, Math answers
Understand mathematics in its entirety, how the various areas, concepts and truths of math unfold.
2017 Proposal: A Research Program for the Big Picture in Mathematics which I submitted, unsuccessfully, for a European Philosophy of Science Association fellowship to study at the Munich Center for Mathematical Philosophy.
- Explore how math concepts connect different branches of math by way of basic structures.
- What is the role of perspectives in math?
- How are perspectives related to objects, concepts, theorems, variables, problems, insights, principles etc.?
- Consider how the principles of life relate to the kinds of answers.
- Consider how the principles of life relate basic math principles with beauty.
I am investigating from the following directions:
- the ways of figuring things out
- the ways that variables are used
- geometries and transformations (for moods)
- visualizations (sequences, hierarchies, networks)
- the areas of math
I am also studying the thinking of mathematicians who take a broader view of mathematics.
The above overview has me want to focus on perspectives. They express how geometry restructures analysis with algebra. And how do they relate to objects, theorems, etc.?
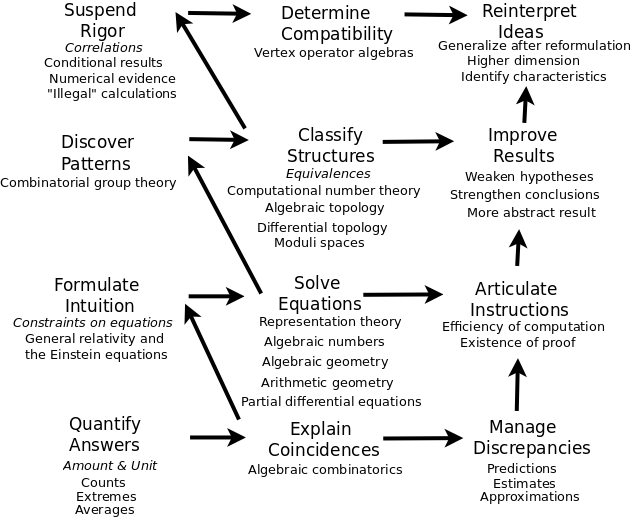
The above diagram relates constructions, equations and instructions. These three remind me of the methods of proof, which similarly consist of equations (bijection, substitution), instructions (induction, separation of cases) and constructions (algorithm construction, construction), and distinguish analytic continuum and algebraic discreteness, as with restructuring. Thus we may have a network of equations, a sequence of instructions, and a hierarchy of constructions, which are restructured, from analysis to algebra.
Constructions, equations and instructions also remind me of category theory, type theory and proof theory, as with the Curry-Howard-Lambek correspondence.
