Introduction E9F5FC

Questions FFFFC0

• View
• Edit
• History
• Print

See: John Baez: Duality in Logic and Physics

I am studying the various cases of duality in math. I imagine that at the heart is the duality between zero and infinity by way of one as in God's Dance. Duality is the basis for logic, and mathematics gives the ways of deviating from duality. Duality is also the structural mirror established within the foursome, fivesome, sixsome and sevensome.

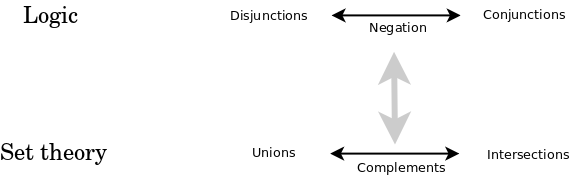
Logic: Duality

Duality arises from a symmetry between two ways of looking at something where there is no reason to choose one over the other. This is driven by the sevensome in defining logic as the balancing of the conscious (not known) and the unconscious (known), what is and what is not (but complements it).

• Logic deals with syntax - external relationships, as in category theory, because it is the syntactic form of the argument which is independent of the actual content.
• Stone's representation theorem for Boolean algebras. Every Boolean algebra is isomorphic to a certain field of sets. Thank you to Eugenijus Paliokas for pointing that out.
• Set theory and first order logic express the same duality of classical logic.
• Generalized by Stone's duality: categorical dualities between certain categories of topological spaces and categories of partially ordered sets. They form a natural generalization of Stone's representation theorem for Boolean algebras. Stone-type dualities provide the foundation for pointless topology and are exploited in theoretical computer science for the study of formal semantics.
• Duality theory for distributive lattices provides three different (but closely related) representations of bounded distributive lattices via Priestley spaces, spectral spaces, and pairwise Stone spaces. This generalizes the well-known Stone duality between Stone spaces and Boolean algebras. There are three equivalent ways of representing bounded distributive lattices. Each one has its own motivation and advantages, but ultimately they all serve the same purpose of providing better understanding of bounded distributive lattices.

Math is subtle deviations from pure duality

These subtle deviations seem to leverage infinity.

• Topology is based on defining open sets to require the inclusion of arbitrary unions but only finite intersections of open sets.
• In ring theory, there is a subtle distinction between the descending chain condition - Artinian rings, and the ascending chain condition - Noetherian rings.

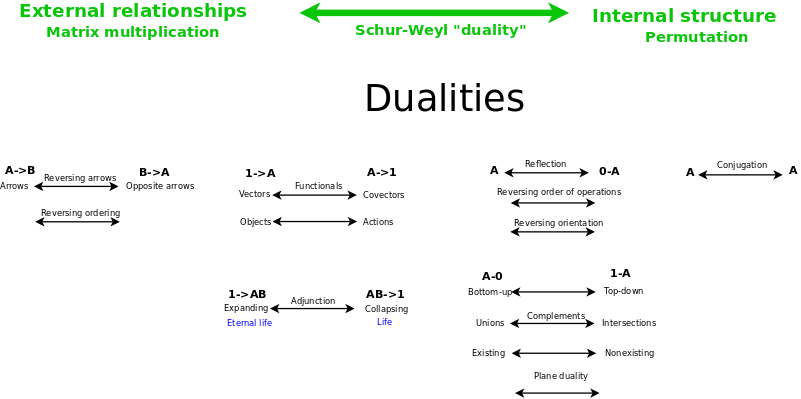
Logic in Mathematics: The Kinds of Duality

Sources of examples of duality

• List of dualities (Wikipedia)
• Wikipedia Category: Duality theories
• nLab: Duality.
• Math Overflow

Involutions

• Involutions
• Involutions are counted by Young tableaux (standard tableaux). So what do special rim hook tableaux count? And can we prove therefore that there is no involution for K-1 K = 1 ? For if there was an involution then we would have a way to deal with all involutions?
• My dream of Young tableaux whose entries were short and long dashes - "this is the fundamental unit of information".
• Tableaux as the square root of a matrix.
• The asymptotic growth of the number of involutions grows as the square root of n. This supports the idea of the involutions as a "square root" of... matrices?

The fundamental anti-duality (Schur-Weyl duality) between external representations and internal structure

• Schur–Weyl duality is a mathematical theorem in representation theory that relates irreducible finite-dimensional representations of the general linear and symmetric groups.
• Four flavors of Schur-Weyl duality
• Tannaka duality An algebra A is reconstructible from the fiber functor on the category of all its modules. (I think: an algebra A is reconstructible from all of its representations.)
  • Tannaka duality: A simple case of Tannaka duality is that of G-sets of a group, i.e. representations on a set. In this case, Tannaka duality follows entirely from repeated application of the ordinary Yoneda lemma.

Anti-duality: Internal structure and external relationships

• This is the point of Hopf algebras: multiplication (generating external structure) is dual to comultiplication (generating internal structure)
• An automorphism (mapping a structure to itself) is an internal isomorphism. Typically, isomorphisms are external.
• This is the duality of category theory: External relationships can restate internal structure.
• Kategorijų teorijos prieštaringumas yra, kad pavyzdžiai yra "objektai" su vidinėmis sandaromis, nors tai kertasi su kategorijų teorijos dvasia.
• Matematika skiria vidines sandaras (semantika) ir išorinius santykius (sintaksė). Užtat labai svarbu mąstyti apie "viską", kuriam nėra išorinių santykių. Panašiai gal būtų galima mąstyti apie nieką, kur nėra vidinės sandaros. Nors viskas irgi neturi vidinės sandaros. Užtat viskam semantika ir sintaksė yra atitinkamai visiškai paprasta.
• Duality between matrices expressed explicitly (in terms of entries) and implicitly (in terms of eigenvalues).
• Math Overflow: How to constructively/combinatorially prove Schur-Weyl duality?
• Peter-Weyl, Howe and Schur-Weyl theorems for current groups
• Skew Howe duality generalizes Schur Weyl duality and makes it look like a duality. See video by Catharina Stroppel. Representation Theory and Categorification. III.

https://arxiv.org/abs/1210.6437

Dualities in the symmetric functions: Elementary and homogeneous; Schur and power; monomial and forgotten?

Anti-Duality: Symmetry and Structure

• A "transformation group" is a group acting as transformations of some set S. Every transformation group is the group of all permutations preserving some structure on S, and this structure is essentially unique. The bigger the transformation group, the less structure: symmetry and structure are dual, just like "entropy" and "information", or "relativity" and "invariance".
• Matrix algebra - linear algebra - like category theory - expresses external relationships. Symmetric groups and their permutations express internal structure. Schur-Weyl duality relates them.

Field With One Element: A Forced Analogy

• The "field with one element" F1 is not a mathematical object; it refers to a collection of analogies between algebra and combinatorics. One central analogy is the idea that {$GL_n(F_1)$} should be the symmetric group {$Σ_n$}. (Barratt-Priddy theorem)

Duality: Translating structures

• Any two structures which have a nice map from one to the other have a duality in that you can start from one and go to the other.
• Galois theory: field extensions (solutions of polynomials) and groups
• Lie groups: solutions to differential equations. Lie's idée fixe was to develop a theory of symmetries of differential equations that would accomplish for them what Évariste Galois had done for algebraic equations: namely, to classify them in terms of group theory. Lie and other mathematicians showed that the most important equations for special functions and orthogonal polynomials tend to arise from group theoretical symmetries. In Lie's early work, the idea was to construct a theory of continuous groups, to complement the theory of discrete groups that had developed in the theory of modular forms, in the hands of Felix Klein and Henri Poincaré. The initial application that Lie had in mind was to the theory of differential equations. On the model of Galois theory and polynomial equations, the driving conception was of a theory capable of unifying, by the study of symmetry, the whole area of ordinary differential equations. However, the hope that Lie Theory would unify the entire field of ordinary differential equations was not fulfilled. Symmetry methods for ODEs continue to be studied, but do not dominate the subject. There is a differential Galois theory, but it was developed by others, such as Picard and Vessiot, and it provides a theory of quadratures, the indefinite integrals required to express solutions.
• de Rham cohomology links algebraic topology and differential topology
• Hilbert's Nullstellensatz
• Class field theory provides a one-to-one correspondence between finite abelian extensions of a fixed global field and appropriate classes of ideals of the field or open subgroups of the idele class group of the field.
• One may ask analytic questions about algebraic numbers, and use analytic means to answer such questions; it is thus that algebraic and analytic number theory intersect. For example, one may define prime ideals (generalizations of prime numbers in the field of algebraic numbers) and ask how many prime ideals there are up to a certain size. This question can be answered by means of an examination of Dedekind zeta functions, which are generalizations of the Riemann zeta function, a key analytic object at the roots of the subject.[79] This is an example of a general procedure in analytic number theory: deriving information about the distribution of a sequence (here, prime ideals or prime numbers) from the analytic behavior of an appropriately constructed complex-valued function.
• In mathematics, monstrous moonshine, or moonshine theory, is a term devised by John Conway and Simon P. Norton in 1979, used to describe the unexpected connection between the monster group M and modular functions, in particular, the j function. It is now known that lying behind monstrous moonshine is a vertex operator algebra called the moonshine module or monster vertex algebra, constructed by Igor Frenkel, James Lepowsky, and Arne Meurman in 1988, having the monster group as symmetries. This vertex operator algebra is commonly interpreted as a structure underlying a conformal field theory, allowing physics to form a bridge between two mathematical areas. The conjectures made by Conway and Norton were proved by Richard Borcherds for the moonshine module in 1992 using the no-ghost theorem from string theory and the theory of vertex operator algebras and generalized Kac–Moody algebras.
• Isbell duality relates higher geometry with higher algebra. nLab: Gelfand duality is the Isbell duality for the case of compact topological spaces and commutative C-star algebras.
• Topos links geometry and logic.
• The AGT correspondence is a relationship between Liouville field theory on a punctured Riemann surface and a certain four-dimensional SU(2) gauge theory obtained by compactifying the 6D (2,0) superconformal field theory on the surface.
• The modularity theorem (formerly called the Taniyama–Shimura–Weil conjecture and several related names) states that elliptic curves over the field of rational numbers are related to modular forms.

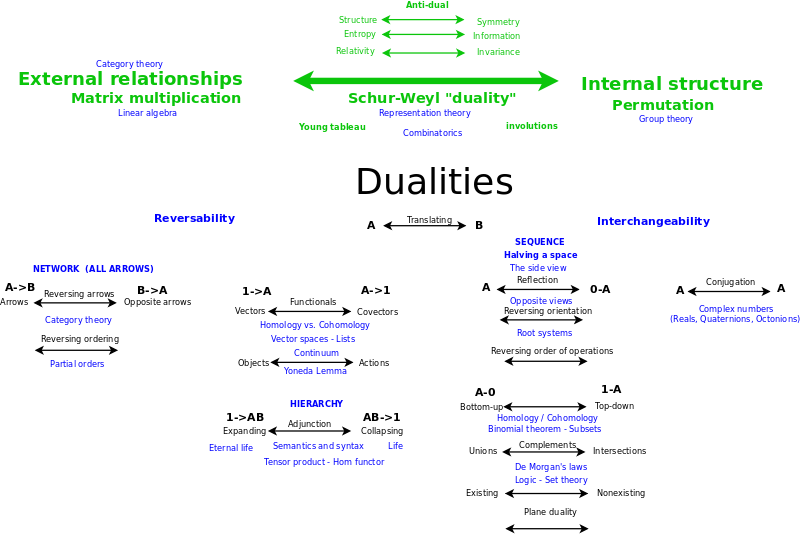
Internal, Implicit Dualities

Duality: Conjugation

• Square roots of -i. There are two square roots of -1. One we call +i, the other -i, but neither should have priority over the other. Similarly, clockwise and counterclockwise rotations should not be favored. Complex conjugation is a way of asserting this. (Note that the integer +1 is naturally favored over -1. But there is no such natural favoring for i. It is purely conventional, a misleading artificial contrivance.)
• Conjugation (ab)* = b*a* is very important in the Cayley-Dickson construction of the numbers: real, complex, quaternion, octonion.
• Conjugation establishes the twosome by way of the Complex numbers. The Reals give the onesome. And this is followed by the Quaternions defining the threesome and so presumably the Octonions define the foursome.

Duality: Halving space: Rotation: Reversing orientation

• Coxeter groups are built from reflections. Reflections are dualities.
• A rectangular matrix can be written out from left to right or right to left. So we have the transpose matrix.
• If G is a group and ρ is a linear representation of it on the vector space V, then the dual representation ρ* is defined over the dual vector space V* as follows: ρ*(g) is the transpose of ρ(g−1), that is, ρ*(g) = ρ(g−1)T for all g ∈ G. A general ring module does not admit a dual representation. Modules of Hopf algebras do, however.

Duality: Reflection

• Dual root system - roots and coroots, given by the inner product, thus by reflection to match the shorter root with the longer root. This is generalized by the root datum of an algebraic group, which furthermore determines the center of a group. The dual root datum is gotten by switching the characters with the 1-parameter subgroups, and the roots with the coroots.
• Given a connected reductive algebraic group G, the Langlands dual group is the complex connected reductive group whose root datum is dual to that of G.

Duality: Reversing order of operations

• Normality says conjugate invariancy: gN = Ng.
• Wikipedia: In applications to logic, this then looks like a very general description of negation (that is, proofs run in the opposite direction). If we take the opposite of a lattice, we will find that meets and joins have their roles interchanged. This is an abstract form of De Morgan's laws, or of duality applied to lattices.
• This is related to the duality between left and right multiplication. Examples include Polish notation.
• For a normal subgroup, the left cosets match the right cosets.

Duality: Bottom-up and Top-down

• Coordinate systems can be organized "bottom up" or "top down". This yields the duality in projective geometry.
• Root systems relate reflections (hyperplanes) and root vectors. Given a root R, reflecting across its hyperplane, every root S is taken to another root -S, and the difference between the two roots is an integer multiple of R. But this relates to the commutator sending the differences into the module based on R.
• Cotangent space and tangent space (or is this between covariant and contravariant?)
• For integers, decomposition into primes is a "bottom up" result which states that a typical number can be compactly represented as the product of its prime components. The "top down" result is that this depends on an infinite number of exceptions ("primes") for which this compact representation does not make them more compact.
• Duality of silence (top-down) and speaking (bottom-up).

Duality: Complements

• Center and totality for a simplex and other infinite families of complex polytopes.
• Duality (projective geometry). Interchange the role of "points" and "lines" to get a dual truth: The plane dual statement of "Two points are on a unique line" is "Two lines meet at a unique point". (Compare with the construction of an equilateral triangle and the lattice of conditions.)
• Poincare duality states that if M is an n-dimensional oriented closed manifold (compact and without boundary), then the kth cohomology group of M is isomorphic to the (n − k)th homology group of M, for all integers k. At the heart of Poincare duality are dual cell structures, which are the foundation for string diagrams, whereby an object, morphism, morphism-between-morphism can be represented by a dot, string, face or by a face, string, dot. Verdier duality is a generalization.
• Twisted Poincaré duality is a theorem removing the restriction on Poincaré duality to oriented manifolds. The existence of a global orientation is replaced by carrying along local information, by means of a local coefficient system.
• Jordan curve theorem (separating the inside and outside of a curve) generalized by the Jordan–Brouwer separation theorem, generalized by Alexander duality about the Betti numbers of the simplicial complex, and in the modern statement, between the reduced homology or cohomology of a compact, locally contractible subspace X of a sphere and its complement Y, Hq(X) and Hn-q-1(Y). Generalized by Spanier–Whitehead duality. Sphere complements determine the homology, and the stable homotopy type, though not the homotopy type.
• Beta-dual space is a certain linear subspace of the algebraic dual of a sequence space.
• The Riemann-Roch theorem relates the complex analysis of a connected compact Riemann surface with the surface's purely topological genus g, in a way that can be carried over into purely algebraic settings. First for Riemann surfaces, then for algebraic curves. Serre duality is present on non-singular projective algebraic varieties V of dimension n (and in greater generality for vector bundles and further, for coherent sheaves). It shows that a cohomology group Hi is the dual space of another one, Hn−i. Coherent duality is a generalization applying to coherent sheaves. Grothendieck local duality is a duality theorem for cohomology of modules over local rings, analogous to Serre duality of coherent sheaves. The Grothendieck–Riemann–Roch theorem from about 1956 is usually cited as the key moment for the introduction of this circle of ideas. The more classical types of Riemann–Roch theorem are recovered in the case where S is a single point (i.e. the final object in the working category C). Using other S is a way to have versions of theorems 'with parameters', i.e. allowing for continuous variation, for which the 'frozen' version reduces the parameters to constants. In other applications, this way of thinking has been used in topos theory, to clarify the role of set theory in foundational matters. Assuming that we don’t have a commitment to one 'set theory' (all toposes are in some sense equally set theories for some intuitionistic logic) it is possible to state everything relative to some given set theory that acts as a base topos.
• In differential geometry, the Atiyah–Singer index theorem, proved by Michael Atiyah and Isadore Singer (1963), states that for an elliptic differential operator on a compact manifold, the analytical index (related to the dimension of the space of solutions) is equal to the topological index (defined in terms of some topological data). It includes many other theorems, such as the Riemann–Roch theorem, as special cases
• Dualizing sheaf.
• Artin-Verdier duality is a duality theorem for constructible abelian sheaves over the spectrum of a ring of algebraic numbers, introduced by Artin and Verdier (1964), that generalizes Tate duality. Tate duality or Poitou–Tate duality is a duality theorem for Galois cohomology groups of modules over the Galois group of an algebraic number field or local field.
• In Galois cohomology, local Tate duality (or simply local duality) is a duality for Galois modules for the absolute Galois group of a non-archimedean local field. It is named after John Tate who first proved it. It shows that the dual of such a Galois module is the Tate twist of usual linear dual. This new dual is called the (local) Tate dual. Local duality combined with Tate's local Euler characteristic formula provide a versatile set of tools for computing the Galois cohomology of local fields. Tate duality is a version for global fields.
• The dualizing complex DX on X is defined to be ... where p is the map from X to a point. Part of what makes Verdier duality interesting in the singular setting is that when X is not a manifold (a graph or singular algebraic variety for example) then the dualizing complex is not quasi-isomorphic to a sheaf concentrated in a single degree.
• The Hodge isomorphism or Hodge star operator is an important linear map introduced in general by W. V. D. Hodge. It is defined on the exterior algebra of a finite-dimensional oriented vector space endowed with a nondegenerate symmetric bilinear form. The result when applied to an element is called the element's Hodge dual.
• Lefschetz duality is a version of Poincaré duality in geometric topology, applying to a manifold with boundary.

Duality: Complements: Plane duality

• Dual graph of a plane graph G is a graph that has a vertex for each face of G. The dual graph has an edge whenever two faces of G are separated from each other by an edge, and a self-loop when the same face appears on both sides of an edge.
• Dual polyhedron
• Tangents
• Dual curve of a given plane curve C is a curve in the dual projective plane consisting of the set of lines tangent to C. There is a map from a curve to its dual, sending each point to the point dual to its tangent line.
• Dual polygon: rectification; polar reciprocation (pole and polar); projective duality; combinatorially.
• Fenchel's duality theorem ... Fenchel's theorem states that the two problems have the same solution. The points having the minimum vertical separation are also the tangency points for the maximally separated parallel tangents.
• Stokes' theorem. Stokes' theorem is a vast generalization of the fundamental theorem of calculus, which states that the integral of a function f over the interval [a, b] can be calculated by finding an antiderivative F of f: General Stokes theorem: duality between the boundary operator on chains and the exterior derivative. Stokes' theorem says that the integral of a differential form ω over the boundary of some orientable manifold Ω is equal to the integral of its exterior derivative dω over the whole of Ω. Stokes' theorem says that this is a chain map from de Rham cohomology to singular cohomology with real coefficients; the exterior derivative, d, behaves like the dual of ∂ on forms. This gives a homomorphism from de Rham cohomology to singular cohomology.

Duality: Existing and nonexisting

• Switching of "existing" and "nonexisting", for example, edges in a graph. This underlies Ramsey's theorem. Tao: "the Ramsey-type theorem, each one of which being a different formalisation of the newly gained insight in mathematics that complete disorder is impossible."
• Duality - parity - išsiaiškinimo rūšis

Intersections and Unions

• Stone duality are categorical dualities between certain categories of topological spaces and categories of partially ordered sets.
  • Schuller on Stone's Theorem
• The dual of the category of frames is called the category of locales and generalizes the category Top of all topological spaces with continuous functions. The consideration of the dual category is motivated by the fact that every continuous map between topological spaces X and Y induces a map between the lattices of open sets in the opposite direction as for every continuous function f: X → Y and every open set O in Y the inverse image f -1(O) is an open set in X.
• Jónsson–Tarski duality General frames bear close connection to modal algebras. ... In the opposite direction, it is possible to construct the dual frame ... A frame and its dual validate the same formulas, hence the general frame semantics and algebraic semantics are in a sense equivalent.
• Inclusion-exclusion principle
• Esakia duality is the dual equivalence between the category of Heyting algebras and the category of Esakia spaces. Esakia duality provides an order-topological representation of Heyting algebras via Esakia spaces.
• Alvis–Curtis duality is a duality operation on the characters of a reductive group over a finite field. Kawanaka introduced a similar duality operation for Lie algebras. The dual ζ* of a character ζ of a finite group G with a split BN-pair is defined to be...

Generated by complements

• De Groot dual of a topology τ on a set X is the topology τ* whose closed sets are generated by compact saturated subsets of (X, τ). Saturated subset is an intersection of open subsets.

External, Explicit Dualities

Duality: Functionals

• Vectors and covectors. A vector is 1-dimensional and a covector is n-1 dimensional hyperplane (tangent plane), see Penrose chapter 12.
• A dual vector space (or just dual space for short) consisting of all linear functionals on V, together with the vector space structure of pointwise addition and scalar multiplication by constants.
• Internal vs. external geometry = implicit vs. embedding = vector space vs. dual space (functionals)
• dual set is a set B∗ of vectors in the dual space V∗ with the same index set I such that B and B∗ form a biorthogonal system. The dual set is always linearly independent but does not necessarily span V∗. If it does span V∗, then B∗ is called the dual basis or reciprocal basis for the basis B.
• Dual basis in a field extension
• Dual bundle of a vector bundle π : E → X is a vector bundle π∗ : E∗ → X whose fibers are the dual spaces to the fibers of E.
• Grothendieck's relative point of view studies and object X by considering instead morphisms f: X → S where S is a fixed object. This idea is made formal in the idea of the slice category of objects of C 'above' S. To move from one slice to another requires a base change; from a technical point of view base change becomes a major issue for the whole approach (see for example Beck–Chevalley conditions). A base change 'along' a given morphism g: T → S is typically given by the fiber product, producing an object over T from one over S.
• Pontryagin duality of a locally compact abelian group G is the group given by maps (characters) from it to the circle group T. The reciprocal lattice is related to this.
• Tannaka–Krein duality theory concerns the interaction of a compact topological group and its category of linear representations. It is a natural extension of Pontryagin duality, between compact and discrete commutative topological groups, to groups that are compact but noncommutative. ... In contrast to the case of commutative groups considered by Lev Pontryagin, the notion dual to a noncommutative compact group is not a group, but a category Π(G) with some additional structures, formed by the finite-dimensional representations of G. The idea of Tannaka–Krein duality: category of representations of a group. A generalization of Tannaka–Krein theory provides the natural framework for studying representations of quantum groups, and is currently being extended to quantum supergroups, quantum groupoids and their dual Hopf algebroids.
• The dual of a universal enveloping algebra, as a vector space, and as one kind of quantum group, Hopf algebra, is another kind of quantum group, Hopf algebra.
• Given the lattice of characters of a maximal torus, the dual lattice is given by the 1-parameter subgroups.
• The Langlands program seeks to relate Galois groups in algebraic number theory to automorphic forms and representation theory of algebraic groups over local fields and adeles.
• The Langlands conjectures imply, very roughly, that if G is a reductive algebraic group over a local or global field, then there is a correspondence between "good" representations of G and homomorphisms of a Galois group (or Weil group or Langlands group) into the Langlands dual group of G. A more general formulation of the conjectures is Langlands functoriality, which says (roughly) that given a (well behaved) homomorphism between Langlands dual groups, there should be an induced map between "good" representations of the corresponding groups. To make this theory explicit, there must be defined the concept of L-homomorphism of an L-group into another. That is, L-groups must be made into a category, so that 'functoriality' has meaning. The definition on the complex Lie groups is as expected, but L-homomorphisms must be 'over' the Weil group.
• Geometric Langlands duality from six dimensions Edward Witten
• Langlands program. An Elementary Introduction to the Langlands Program by Stephen Gelbart.Langland Frenkel. 6D (2,0) superconformal field theory.
• Dual object is a category theory generalization of the concept of dual space in linear algebra.
• When dealing with topological vector spaces, one is typically only interested in the continuous linear functionals from the space into the base field F = C or R. A Continuous dual space or topological dual is a linear subspace of the algebraic dual space V and V'. For any finite-dimensional normed vector space or topological vector space, such as Euclidean n-space, the continuous dual and the algebraic dual coincide.
• In functional analysis and related areas of mathematics a dual topology is a locally convex topology on a dual pair, two vector spaces with a bilinear form defined on them, so that one vector space becomes the continuous dual of the other space. The different dual topologies for a given dual pair are characterized by the Mackey–Arens theorem. All locally convex topologies with their continuous dual are trivially a dual pair and the locally convex topology is a dual topology.
• A dual pair or dual system is a pair of vector spaces with an associated bilinear map to the base field. A dual pair generalizes this concept of continuous dual to arbitrary vector spaces, with the duality being expressed as a bilinear map. Using the bilinear map, semi norms can be constructed to define a polar topology on the vector spaces and turn them into locally convex spaces, generalizations of normed vector spaces.
• A dual wavelet is the dual to a wavelet. In general, the wavelet series generated by a square integrable function will have a dual series, in the sense of the Riesz representation theorem. The Hilbert space representation theorem establishes an important connection between a Hilbert space and its (continuous) dual space. If the underlying field is the real numbers, the two are isometrically isomorphic; if the underlying field is the complex numbers, the two are isometrically anti-isomorphic. The (anti-) isomorphism is a particular, natural one.
• The Riesz–Markov–Kakutani representation theorem relates linear functionals on spaces of continuous functions on a locally compact space to measures.
• The dual space X' of a stereotype space is defined as the space of all linear continuous functionals f : X → C endowed with the topology of uniform convergence on totally bounded sets in X.
• Dual abelian variety can be defined from an abelian variety A, defined over a field K. To an abelian variety A over a field k, one associates a dual abelian variety Av (over the same field), which is the solution to the following moduli problem. ... the points of Av correspond to line bundles of degree 0 on A, so there is a natural group operation on Av given by tensor product of line bundles, which makes it into an abelian variety. There is a general form of duality between the Albanese variety of a complete variety V, and its Picard variety.
• Weil pairing is generalized by Cartier duality, which is an analogue of Pontryagin duality for noncommutative schemes.

Duality: Actions and Objects

• We can look at the operators that act or the objects they act upon. This brings to mind the two representations of the foursome.
• The Yoneda Lemma gives our connection to Why, and collapsing a network's node or relating it to its arrows. Relationship with Why as given by the eightfold way.

Duality: Adjunction

• Adjoint bendrai ir Adjoint functors. The minimialistic solution - the maximalist problem solved. The most efficient solution - the most difficult problem solved. Wikipedia: It can be said that an adjoint functor is a way of giving the most efficient solution to some problem via a method which is formulaic. A construction is most efficient if it satisfies a universal property, and is formulaic if it defines a functor. Universal properties come in two types: initial properties and terminal properties. Since these are dual (opposite) notions, it is only necessary to discuss one of them.
• A functor F : C ← D is a left adjoint functor if for each object X in C, there exists a terminal morphism from F to X. A functor G : C → D is a right adjoint functor if for each object Y in D, there exists an initial morphism from Y to G.
• A counit–unit adjunction between two categories C and D consists of two functors F : C ← D and G : C → D and two natural transformations...
• A hom-set adjunction between two categories C and D consists of two functors F : C ← D and G : C → D and a natural isomorphism...
• Example of adjoint functors Given inclusion i:Z->R, with morphism x->y in R whenever x<=y, then the right adjoint is the floor function and the left adjoint is the ceiling function. A pair of adjoint functors is what is needed to make two categories compatible in their objects and morphisms.
• A very general comment of William Lawvere is that syntax and semantics are adjoint: take C to be the set of all logical theories (axiomatizations), and D the power set of the set of all mathematical structures. For a theory T in C, let F(T) be the set of all structures that satisfy the axioms T; for a set of mathematical structures S, let G(S) be the minimal axiomatization of S. We can then say that F(T) is a subset of S if and only if T logically implies G(S): the "semantics functor" F is left adjoint to the "syntax functor" G. Peter Smith. The Galois Connection between Syntax and Semantics.
  • Posina Venkata Rayudu, see here and here: According to Professor F. William Lawvere: Syntax is NOT the adjoint of semantics
• division is (in general) the attempt to invert multiplication, but many examples, such as the introduction of implication in propositional logic, or the ideal quotient for division by ring ideals, can be recognised as the attempt to provide an adjoint.
• Tensor products are adjoint to a set of homomorphisms.
• The two facts that this method of turning rngs into rings is most efficient and formulaic can be expressed simultaneously by saying that it defines an adjoint functor. Continuing this discussion, suppose we started with the functor F, and posed the following (vague) question: is there a problem to which F is the most efficient solution? The notion that F is the most efficient solution to the problem posed by G is, in a certain rigorous sense, equivalent to the notion that G poses the most difficult problem that F solves.
• Consider an object Y in a category with pullbacks. Any morphism f : X → Y induces a functor f ∗ : Sub ( Y ) ⟶ Sub ( X ) on the category that is the preorder of subobjects. It maps subobjects T of Y (technically: monomorphism classes of T → Y to the pullback X × Y T ). If this functor has a left- or right adjoint, they are called ∃ f and ∀ f, respectively.[3] They both map from Sub ( X ) back to Sub ( Y ) . Very roughly, given a domain S ⊂ X to quantify a relation expressed via f over, the functor/quantifier closes X in X × Y T and returns the thereby specified subset of Y.

Duality: Reversing the maps

• Dual (category theory)
• Opposite category. Morphisms can be organized from left to right or from right to left. The opposite category turns all of the arrows around.
  • If a category is equivalent to the opposite (or dual) of another category then one speaks of a duality of categories, and says that the two categories are dually equivalent.
  • Colimits and limits
  • Monomorphisms ("one-to-one") and epimorphisms (forcing "onto").
  • Coproducts and products
  • Initial and terminal objects
  • Covariance and contravariance
  • Wikipedia: Fibrations and cofibrations are examples of dual notions in algebraic topology and homotopy theory. In this context, the duality is often called Eckmann–Hilton duality.
  • L.Lafforgue When one considers a concrete category, replacing it by the opposite category most often completely changes the point of view and, in particular, the constructions of limits and colimits in a given category most often do not have the same level of difficulty and depth at all. For example, the opposite of the algebraic category C of commutative rings is the category of affine schemes to which all the usual vocabulary of geometry applies whereas it does not apply at all to C. Generally speaking, when one category can be considered "geometric", the opposite category cannot be considered "geometric" at all. In a "geometric" category, the limits that are well defined are usually relatively elementary, whereas the colimits are usually much more subtle, deeper and mathematically richer. This fundamental asymmetry of geometry is reflected in particular by the fact that the opposite category of a topos (different from the trivial topos with a single object and a single morphism) is never a topos. In particular, the opposite of the category Set is not a topos and, already in Set, the construction of colimits, i.e. quotient sets, is more subtle and richer than the construction of limits, i.e. subsets defined by equations. On the other hand, the proper of linear properties is to be symmetrical: the opposite of an additive category is an additive category, and the opposite of an abelian category is an abelian category. This means in particular that all cohomological functors, which are defined from "geometrical" categories to "linear" categories, go from a fundamentally asymmetrical world to a symmetrical world. Going to the symmetrical world of linear structures makes it possible for "dualities" to appear: Poincaré's duality and its reinterpretation and generalisation by Grothendieck in what he called the "formalism of the six operations" are at the centre of the linearisation of geometry by cohomological fonctors.
  • Pierre-Alain Jacqmin The geometric world and the algebraic world are in some sense dual to each other. The dual of the category of topological spaces is (quasi)-algebraic, the dual of the category of affine scheme is the category of commutative rings, the dual of the category of locales is the category of frames, the dual of the category of compact Hausdorff spaces is the category of commutative unital C*-algebras, etc. Since those two worlds are dual to each other, but in each of them limits are easier to understand than colimits, this means that the equivalences appearing in these dualities contain a lot of information. Moreover, the case of the category of sets which trivially belongs to both worlds is intriguing, but confirms that, intrinsically, limits are easier to understand than colimits
  • L.Lafforgue For any field k, the category of finite dimensional vector spaces over k is self-dual : it is naturally equivalent to its opposite category. This was generalised by Grothendieck to the context of categories of linear sheaves. As these categories have non trivial local Ext cohomology, the abelian categories of linear sheaves have to be replaced by their associated derived categories to make possible some self-duality. Furthermore, the "finite dimension" condition has to be replaced by a requirement that the sheaves under consideration are "constructible" in some sense. This is part of Grothendieck's "six operations formalism".
• Every isomorphism is a duality in that it goes hand in hand with its inverse. If the domain and codomain are the same, then it is self-dual.
• Duality (order theory). Every partially ordered set P gives rise to a dual (or opposite) partially ordered set which is often denoted by Pop or Pd. This dual order Pop is defined to be the set with the inverse order. Dual properties:
  • Greatest elements and least elements
  • Maximal elements and minimal elements
  • Least upper bounds (suprema, ∨) and greatest lower bounds (infima, ∧)
  • Upper sets and lower sets
  • Ideals and filters
  • Closure operators and kernel operators.
• Self-dual notions:
  • Being a (complete) lattice
  • Monotonicity of functions
  • Distributivity of lattices, i.e. the lattices for which ∀x,y,z: x ∧ (y ∨ z) = (x ∧ y) ∨ (x ∧ z) holds are exactly those for which the dual statement ∀x,y,z: x ∨ (y ∧ z) = (x ∨ y) ∧ (x ∨ z) holds
  • Being a Boolean algebra
  • Being an order isomorphism.
• Since partial orders are antisymmetric, the only ones that are self-dual are the equivalence relations.

Duality: Reversing the ordering

• Wikipedia: Reversing the direction of inequalities in a partial order. (Partial orders correspond to a certain kind of category in which Hom(A,B) can have at most one element.)
• Analysis provides lower and upper bounds on a function or phenomenon which helps define the geometry of this space.

Other

• Araki duality for free fields: the commuting algebra of the local algebra of a region O in space-time is equal to the local algebra of the set of points that are spacelike separated from O.

Mathematics: Almost Duality - Duality Breaking

The duality between zero and infinity, between nothing and everything, is broken in many subtle ways. Here are some examples:

• By definition, a topological space includes both an entire set X and the empty set. However, the intermediary sets are closed under arbitrary unions, but only finite intersections. What would happen if they were closed under infinite intersections?
• Perhaps similarly, having in mind the Zariski topology, ideals of a ring are defined with respect to multiplication (union) but not addition (intersection).
• Meromorphic function is the quotient of two holomorphic functions, thus compares them.

Dual values

• Usually the term "dual problem" refers to the Lagrangian dual problem but other dual problems are used, for example, the Wolfe dual problem and the Fenchel dual problem.
• In Wolfe duality, the objective function and constraints are all differentiable functions. Using this concept a lower bound for a minimization problem can be found because of the weak duality principle.
• In mathematical optimization theory, duality or the duality principle is the principle that optimization problems may be viewed from either of two perspectives, the primal problem or the dual problem. The solution to the dual problem provides a lower bound to the solution of the primal (minimization) problem.[1] However in general the optimal values of the primal and dual problems need not be equal. Their difference is called the duality gap. For convex optimization problems, the duality gap is zero under a constraint qualification condition.
• The duality gap is the difference between the values of any primal solutions and any dual solutions. The duality gap is zero if and only if strong duality holds. Otherwise the gap is strictly positive and weak duality holds.
• In computational optimization, another "duality gap" is often reported, which is the difference in value between any dual solution and the value of a feasible but suboptimal iterate for the primal problem. This alternative "duality gap" quantifies the discrepancy between the value of a current feasible but suboptimal iterate for the primal problem and the value of the dual problem; the value of the dual problem is, under regularity conditions, equal to the value of the convex relaxation of the primal problem

Mathematical Tension: Equivalence and Uniqueness

In Math, there is an everpresent tension between the notions of equivalence class and uniqueness. If something is mathematically significant, it should in some sense be unique. But math is a model and so, as such, can never be entirely unique but represents a variety of cases. Thus it is ever natural to define equivalence classes, especially in math itself. For example, a rational number is an equivalence class that establishes a proportion.

Ways of figuring things out

• Duality of the deep and the broad.
• Įvairios simetrijos - išsiaiškinimo būdų sandaros.

Duality in Physics

Duality in Mathematics and Physics by Sir Michael Atiyah

Conjugation

• Electricity and magnetism - Electrical circuits In special relativity, applying the Lorentz transformation to the electric field transforms it into a magnetic field. This duality is related to the Langlands duality between a group and its Langlands group.

Complements

• S-duality strong coupling - weak coupling. Realizations include Seiberg duality, Montonen–Olive duality, Generalizes Maxwell duality. Anton Kapustin and Edward Witten suggested that the geometric Langlands correspondence can be viewed as a mathematical statement of Montonen–Olive duality.

Functionals

• T-duality
• AdS/CFT correspondence
• SYZ conjecture
• Mirror symmetry

More:

The transpose of a linear map between two vector spaces, defined over the same field, is an induced map between the dual spaces of the two vector spaces

Duality breaking

• Duality breaking allows that God is good and not bad. Because we want to break the duality of good and bad, increasing and decreasing slack. Orientation is a complete, absolute, total distinction between inside and outside, their complete segregation and isolation. (In contrast to the yin-yang symbol.) So it is highly tenuous - it can break at any single point - but it can eternally grow more weighty.
• Duality breaking (for slack) - disconnecting the local and the global - for example, defining locally Euclidean spaces - in lattice terms, as a consequence of limiting processes, disconnecting the inf from the sup, breaking their duality.
• The Cayley-Dickson construction is all about duality breaking. It thereby yields noncommutativity, nonassociativity, etc.
• A vector is 1-dimensional (and its dimension) and its covector is n-1 dimensional (it is normal to the vector). In this sense they complement each other.
• Vectors are described in terms of partial derivatives (based on the local coordinate systems) whereas covectors are described in terms of (total) forms dx.
• Inner products are sesquilinear - they have conjugate symmetry - so as not to yield lopsided answers. If they yield a complex root as an answer, then one version should yield one root and the other version should yield the other root. In other words, in a complex field, the inner product should be thought of as yielding two answers - both answers - distinguished by the notation, left-right or right-left.
• Kai užsimirštame, kai žinojimas tampa nežinojimu (pavyzdžiui, metant monetą) tada iškyla jungtinės priešingybės (conjugates).
• Electrical duality Topology and Elementary Electric Circuit Theory, II: Duality Tony Phillips

Note that turns left and right are conjugates but not a division of everything because there can be no turn. Instead, the twosome is "turn" (left/right) and "no-turn". "Turn" does not need to be marked, but "no-turn" needs to be marked ("no"). Although, content-wise, not-turning is unmarked and turning is marked.

This duality between compact and non-compact symmetric spaces is a generalization of the well known duality between spherical and hyperbolic geometry. Wikipedia: List of simple Lie groups: Symmetric spaces

Tannaka duality

Cohomology at nLab: Cohomology is dual to homotopy (as an operation): the cohomology of X with coefficients in A is the homotopy of A with co-coefficients in X. Cohomology should be thought of as "cohomotopy". For any {$A\in H$} the set {$H(S^n,A)$} is equivalently:

• the A-cohomology of {$S^n$}
• the nth homotopy group of A

Examples in Math Companion:

• Platonic solids
• Points and lines in the projective plane
• Sets and their complements
• Dual vector spaces
• Polar bodies
• Duals of Abelian groups
• Homology and cohomology
• Differential forms: k-forms and k-dimensional surfaces
• Distributions: ...
• Mirror symmetry: (conjectural) Calabi-Yau manifolds and mirror manifolds
• Fourier transform?
• Representation theory: Langlands dual of certain non-Abelian groups

Another key concept for me is the idea of an "unmarked opposite" vs. a "marked opposite".

• We can have what is beyond a system be identified with an opposite within the system. For example, a blank sheet of paper can be noted by the empty set. The empty set is opposite to nonempty sets. And there is a sense in which the empty set is preferred, is central. Or we can have the identity element of a group which expresses no action at all. Similarly, good can be distinguished from bad by claiming that God is good, where God is what is beyond the system. So here in this sense I say that good is the marked opposite, the one identified with what is beyond the system.
• Also, in a different sense, in a system, a marked opposite is when you have two opposites (choices) that are clearly distinguished and one is the default (thus preferred) because it is unmarked, whereas the other one is marked to distinguish it and thus secondary. For example, 1 and -1. 1 is unmarked and -1 is marked (and it actually has an extra mark). And they are clearly distinct: -1 x -1 = 1 whereas 1 x 1 = 1.
• Finally, we can have "unmarked opposites" where two choices are distinct but otherwise not distinguishable. They have yet to be marked. For example, the two square roots of -1. One will imagined clockwise, the other counterclockwise, perhaps. But which is which doesn't matter. Only when we name them using + and -, only when we attribute such a prejudice to them, do we lose touch with their original indistinguishability, thus ending up with i and -i, forgetting that -i is no less basic than +i.

So I'm very interested where such dualities and opposites come up in math.

Unmarked opposite

• turinys = raiška. "Those things are which show themselves to be." buvimo pagrindas
• inner 2-cycle, kurio paprastai nebūna.
• complex numbers i=j iš kurio atsiveria 1<>-1, i<>-i. Paprastai i -> j -> i ... banguoja, o šitą sustabdžius gaunasi +1 +1 +1 +1 amžinai ir atitinkamai -1-1-1-1 amžinai.

Notes

Duality

• Duality of nonrelevance in system (kernel) and nonrelevance beyond system (cokernel).
• Compare the kinds of dualities with the kind of transformations of perspectives and then with the kinds of geometric transformations.
• In the automata hierarchy, consider how to model duality of internal structure and external network.
• Duality of vectors and covectors (linear functionals) - flipsides of composition - what is "inside" and "outside" the composer.
• Conjugates can be thought of as "twins", whereas +1 and -1 are "spouses".
• Conjugate = mystery = false. (Hidden distinction).
• i->j is asymmetric, one-directional. i<->i* is symmetric, two-directional, breaks anti-symmetry, hides anti-symmetry (which is i and which is j?)
• Algebra - geometry duality. (Pullback). Morphism <-> ring homomorphism. Intrinsic and extrinsic geometry. Ambient space. Relation between two spaces. Varieties [morphisms X to Y] <-> Affine F-algebras [F-linear ring homomorphisms F[Y] to F[x]]
• Study the idea behind linear functionals, fundamental representations, eigenvectors, cohomology, and other maps into one dimension.
• Duality examples (conjugates)
  • complex number "i" is not one number - it is a pair of numbers that are the square roots of -1
  • spinors likewise
  • Dn where n=2
  • the smallest cross-polytope with 2 vertices
  • taking a sphere and identifying antipodal elements - this is a famous group
  • polar conjugates in projective geometry (see Wildberger)
  • Study how Set breaks duality (the significance of initial and terminal objects).
• Each physical force is related to a duality:
  • Charge (matter and antimatter) - electromagnetism
  • Weak force - time reversal
• So the types of duality should give the types of forces.
• John Baez on duality: Dyson's Threefold Way: either X is not isomorphic to its dual (the complex case), or it is isomorphic to its dual (in the real or quaternionic cases). Study his slides!
• John Baez on duality in logic and physics
• Algebra (of the observer) and analysis (of the observed) exhibit a duality of worldviews.
• The interpretation {$\mathbb{C} \leftrightarrow \mathbb{R}^2$} gives meaning to the two axes. One axis the opposites 1 and -1 and the other axis is the opposites i and j. And they become related 1 to i to -1 to j. Thus multiplication by i is rotation by 90 degrees. It returns us not to 1 but sends us to -1.
• Composition algebra. Doubling is related to duality.
• Linear functionals. One-dimensional economic thinking is like linear functionals - the dual space of the multidimensional reality. In finite dimensions, the dual dual is the same as what we started. But in infinite dimensions not necessarily. Does this suggest that our life is infinite-dimensional, which is to say, it can't be captured by a one-dimensional shadow?
• Dualities related to the separation of various kinds of "pre" and "post" operations as occur with the Yoneda lemma.
• Hypothesis: Logical connectives ("the gadgets") express the various forms of duality.
• Is the notion of cohomology symmetric in a way that homology is not? (By analogy, is homology like the natural numbers, and cohomology like the integers?)
• David Ellerman. The Logical Theory of Canonical Maps About duality.
• David Ellerman. On the Duality between Existence and Information.

Opposites

• Exercise: Find all matrices with eigenvalues 1 and -1. {$\lambda=\frac{a_{11}+a_{22} \pm \sqrt{(a_{11}+a_{22})^2 - 4|A|}}{2}$} so |A|=-1.

{$\begin{pmatrix} \pm \sqrt{1 + a_{12}a_{21}} & a_{12} \\ a_{21} & \mp \sqrt{1 + a_{12}a_{21}} \end{pmatrix}$} such as {$\begin{pmatrix} 0 & -1 \\ 1 & 0 \end{pmatrix}\begin{pmatrix} i & 0 \\ 0 & -i \end{pmatrix}\begin{pmatrix} 0 & i \\ i & 0 \end{pmatrix}$}

• Multiplying by {$\begin{pmatrix} x \\ y \end{pmatrix}$} yields three ways of coding opposites: {$\begin{pmatrix} iy \\ ix \end{pmatrix}$} {$\begin{pmatrix} -y \\ -x \end{pmatrix}$} {$\begin{pmatrix} ix \\ -iy \end{pmatrix}$} where in each case two of three are applied: flipping, multiplying by i, multiplying by -1.
• Adjunction is a form of duality.
• Equality and equivalence, in general, are forms of duality.
• Duality is an extension of equivalence where the two sides of the equation are somehow different. For example, one side may be a variable and the other side a value that it is set to.
• Conjugates i and j are the form of duality that is the same as equality. Except that they are not identified as such.
• Duality (opposites coexist) and equality (all is the same) form a duality, as in the twosome.

Duality

• The breaking of duality in topology (in the definition of open sets) relates the discrete and the continuous.
• Multiplication is nonidentity - the factors are treated as having noncomparable elements. Whereas duality inverts, bijects and identifies matching elements as the same.

There is a duality between the two evaluation strategies known as call-by-name and call-by-value. This is expressed by the symmetry of sequent calculus.

• the dual space suggests that maps to a one-dimensional space (like money) are equivalent to the multi-dimensional space. But is that true in the case of money? And does that mean that in life we are in the infinite-dimensional case where the dual dual is not the same as what we started with?
• There is a duality between operations in set theory and logical connections. Topos theory shows what about sets makes this work and thus how to generalize that with topology and with category theory.
• AdS/CFT_correspondence

Stone-Weyl duality

• Catharina Stroppel. Representation Theory & Categorification.
• Frobenius reciprocity Restriction and induction are adjoint functors. In the case of finite groups, they are actually both left- and right-adjoint to one another.

Commutative algebra ^op = Geometry

nLab: State has a table of dualities between algebra and geometry.

Yevgeny B. Karasik. Duality revolution: Discovery of new types and mechanisms of duality that are revolutionizing science and technology as well as our ability to solve problems

nLab: syntax-semantics duality