Introduction E9F5FC

Questions FFFFC0

• View
• Edit
• History
• Print

See: Math, Discovery, 20110402 Math Deep Structure, 20160620 Discovery in Mathematics, Math Discovery Examples, Variables

Discovery in Mathematics: A System of Deep Structure

I'm now rewriting the above article in two parts:

• Mathematics Expresses Discovery
• Mathematics Unfolds Through Ambiguity

Notes

• Algebra studies particular structures and substructures.

Zermelo-Fraenkel axioms of set theory

• Axiom of Extensionality. Two sets are the same set if they have the same elements.
• Axiom of Regularity. Every non-empty set x contains a member y such that x and y are disjoint sets. This implies, for example, that no set is an element of itself and that every set has an ordinal rank.
• Axiom Schema of Specification. The subset of a set z obeying a formula ϕ(x) with one free variable x always exists.
• Axiom of Pairing. If x and y are sets, then there exists a set which contains x and y as elements.
• Axiom of Union. The union over the elements of a set exists.
• Axiom Schema of Replacement. The image of a set under any definable function will also fall inside a set.
• Axiom of Power Set. For any set x, there is a set y that contains every subset of x.
• Well-Ordering Theorem. For any set X, there is a binary relation R which well-orders X.

Also:

• Axiom of infinity. Let S(w) abbreviate w ∪ {w}, where w is some set. Then there exists a set X such that the empty set ∅ is a member of X and, whenever a set y is a member of X, then S(y) is also a member of X.

Implicit math: Sets are simplexes. Are simplexes defined by their subsimplexes as well?

• Well-ordering theorem. Each vertex is related by edges to the other vertices. Established by the q-weight.
• Axiom of power set. The power sets are the lattice paths in Pascal's triangle.
• Axiom of union. Simplexes combine to form larger simplexes.
• Axiom of pairing. Simplexes can be "collapsed" or "represented" by a vertex, the highest vertex. Two vertices are linked by an edge.
• Axiom of regularity.
• Axiom of extensionality. Simplexes are defined by their vertices. And the edges?

Eightfold way

• Axiom of Pairing. If x and y are sets, then there exists a set which contains x and y as elements.
• Axiom of Extensionality. Two sets are the same set if they have the same elements.
• Axiom of Union. The union over the elements of a set exists.
• Axiom of Power set. For any set x, there is a set y that contains every subset of x.
• Axiom of Regularity. Every non-empty set x contains a member y such that x and y are disjoint sets.
• Well-ordering theorem. For any set X, there is a binary relation R which well-orders X.
• Axiom Schema of Specification. The subset of a set z obeying a formula ϕ(x) with one free variable x always exists.
• Axiom Schema of Replacement. The image of a set under any definable function will also fall inside a set.

Reorganizings

• Evolution. Tree of variations. Axiom of Pairing (subbranches are part of a branch).
• Atlas. Adjacency graph. Axiom of Extensionality. Two levels of equality.
• Handbook. Total order. Well-Ordering Theorem.
• Chronicle. Powerset lattice. Axiom of Power Set.
• Catalog. Decomposition. Axiom of Union.
• Tour. Directed graph. Axiom of Regularity.

Relate to multiplication

Attach:multiplicationmodels.png Δ

Notes

In algebraic problem solving, we are working in the level, one sheet of paper. In analytic problem solving, we are working in the meta level, above the many sheets of paper.

Total order is the same as a labeled simplex.

Extension: 3! + (4 + 4 + 4 + 6) = 4!

3! = 2! + 4 (representations: 2 for edge and 4 for vertex)

We may assign the weight q^(k-1) to the kth vertex and the weights 1/q to each new edge. These weights give each vertex a unique label. The weight of each k-simplex is then the products of the weights of their vertices and edges. The Gaussian binomial coefficients count these weighted k-simplexes. Without the weights the vertices are distinct but there is no way to distinguish them. The symmetry group is the Symmetric group which relabels the vertices.

Matematikos išsiaiškinimo būdai

• Alexander Bogomolny sarašas

Ways of figuring things out in mathematics

Discovery. What are the ways of figuring things out in mathematics? We can study mathematics as an activity by which we create and solve mathematical problems. The techniques and structures that we use in our minds are much more elemental than the mathematical output which they generate.

I have described and systematized 24 ways of figuring things out in mathematics. I now want to relate that to an overall methodology for answering mathematical questions.

A Conversation with Gary Klein. How firefighters deal with challenges on-the-fly.

I'm giving a talk on the ways of figuring things out in Mathematics.

It's based on a letter that I wrote about a comprehensive system that I organized of 24 such ways.

It needs to be 10 minutes long, 1,000 words.

Discovery in Mathematics: A System of Deep Structure

I will talk about how we may systematically study the ways of figuring things out in mathematics.

George Polya, in his book, "How to Solve It", considers Euclid's problem of how to construct an equilateral triangle. If we are given the side AB, how do we construct the other two? The solution is a recurring idea which Polya calls the "pattern of two loci". We think of there being two separate conditions. One side must extend a length AB from the point A. Another side must extend a length AB from the point B. We thus draw two circles of radius AB centered at A and B. The points where the two circles intersect are those where we can draw a third point C which satisfies both conditions so that our triagle is equilateral.

I realized that our minds solve this problem by imagining a powerset lattice of conditions. Circle A is one condition, circle B is another condition, and the intersection of A and B satisifies the union of these two conditions. Our minds have thus solved the surface problem (constructing a triangle) by considering a simpler, deeper structure (a lattice of conditions). This brings to mind linguist Noah Chomsky's work in syntax and architect Christopher Alexander's work on pattern languages.

I collected such problem solving patterns discussed in Paul Zeitz's book "The Art and Craft of Problem Solving" and other sources. Each distinct pattern makes use of a structure which is familiar to mathematicians and yet is not explicit but mental. We may consider those math structures to be cognitively "natural" which are used by the mind in solving math problems. I present to you 24 patterns which I identified and systematized them in a way which suggests they are complete.

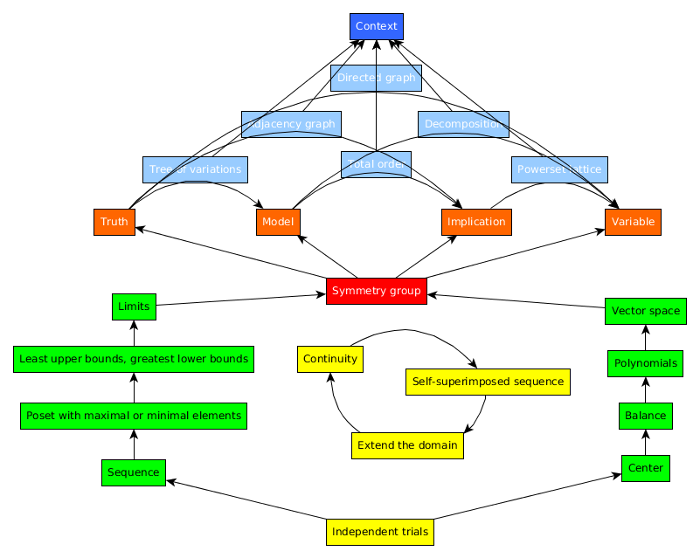
The system distinguishes between

We may always start a fresh sheet (independent trials).

cognitive structures used on a single mental "sheet", as in algebra (center, balance, polynomials, vector spaces),

those that suppose an endless sequence of sheets, as in analysis (sequence, poset with maximal or minimal element, least upper bounds or greatest lower bounds, limits).

Sheets may be "stitched together" (extend the domain, continuity, self-superimposed sequence).

Algebraic and analytic approaches thus combine to give a complete, explicit system (symmetry group).

Within a system, we can relate an explicit sheet where it has fixed expression with an implicit mental sheet where it is imagined and worked on (truth, model, implication, variable).

We can then manipulate a problem explicitly as one of six visualizations of a graph structure (tree of variations, adjacency graph, total order, powerset lattice, decomposition, directed graph).

However, the meaning of any explicit expression such as 10+4= ultimately depends on what is implicit, whether we have in mind, for example, the integer Z or a clock Z12 (context).

• The Pairing axiom can be defined from other Zermelo Fraenkel axioms. (How?) And what does that mean for my identification of the axioms with the ways of figuring things out?

George Polya's book "How to Solve It" showed how we can collect recurring cognitive "patterns" which mathematicians apply intuitively in a variety of settings. For example, in drawing an equilateral triangle, given the first side AB, how do we draw the other two? Using the "pattern of two loci", we draw circles of radius AB centered at A and B and find their intersections. I note here that, in solving this problem, our mind constructs a lattice of conditions on the solution: the plane (no condition), circle A (one condition), circle B (one condition) and the intersection of A and B (two conditions). Thus the surface problem (constructing a triangle) is solved in the mind by considering a simpler, deeper structure (a lattice of conditions). This brings to mind linguist Noah Chomsky's work in syntax and architect Christopher Alexander's work on pattern languages.

I collected such problem solving patterns discussed in Paul Zeitz's book "The Art and Craft of Problem Solving" and other sources. [1] Each distinct pattern makes use of a structure which is familiar to mathematicians and yet is not explicit but mental. We may consider those math structures to be cognitively "natural" which are used by the mind in solving math problems. I identified 24 patterns and systematized them in a way which suggests they are complete. I will present this system as drawn and described in more detail at [2].

The system distinguishes between cognitive structures used on a single mental "sheet", as in algebra (center, balance, polynomials, vector spaces), and those that suppose an endless sequence of sheets, as in analysis (sequence, poset with maximal or minimal element, least upper bounds or greatest lower bounds, limits). We may always start a fresh sheet (independent trials). Sheets may be "stitched together" (extend the domain, continuity, self-superimposed sequence). Algebraic and analytic approaches thus combine to give a complete, explicit system (symmetry group). Within a system, we can relate an explicit sheet where it has fixed expression with an implicit mental sheet where it is imagined and worked on (truth, model, implication, variable). We can then manipulate a problem explicitly as one of six visualizations of a graph structure (tree of variations, adjacency graph, total order, powerset lattice, decomposition, directed graph). However, the meaning of any explicit expression such as 10+4= ultimately depends on what is implicit, whether we have in mind, for example, the integer Z or a clock Z12 (context).

Notes

• Consider how the four levels of geometry-logic bring together the four levels of analysis and the four levels of algebra, yielding the 12 topologies. And why don't the two representations of the foursome yield a third representation?
• Extension of a domain - Analytic continuation - complex numbers - dealing with divergent series.
• Root systems relate two spheres - they relate two "sheets". Logic likewise relates two sheets: a sheet and a meta-sheet for working on a problem. Similarly, we model our attention by awareness, as Graziano pointed out. This is stepping in and stepping out.
• Mathematical mind/brain unites logical language (left brain - logical reasoning) with spatial visual thinking (right brain - geometric intuition). Consider what this means as two parallel ways of thinking for the 4 logic-geometry levels in the ways of discovery.
• geometry (bundle) links algebra (fiber) with analysis (base) and the latter manifold is also understood (ambiguously) algebraically as a Lie group. Algebra is a (finite) cognitive pattern that restructures the (infinite) Analysis, the model of the world. Together they are a restructuring. In the house of knowledge for mathematics, the three-cycle relates analysis and algebra as structuring and restructuring. Thus this restructuring (the six restructurings) is the output of the house of knowledge and the content of mathematics, its branches, concepts, statements, problems, etc.
• Analysis is the infinity of sheets, the recurring sequence of not going beyond oneself. But algebra is the single sheet which is the self that it all goes into, where all of the actions, all of the sheets coincide as one sheet, one going beyond. Thus the cardinal (of algebra) arises from the ordinal (of analysis).
• The ordinal (list) is deterministic whereas the cardinal (set) is nondeterministic.

(polynomial coefficient) Ordinal/List/Analysis vs. Cardinal/Set/Algebra (polynomial root) - the coefficients and roots are related by the binomial theorem, the factors are choices.

• Are there 6+4 branches of math? How are the branches of math related to the ways of figuring things out?
• Proceed from balance - note how additive balance precedes multiplicative ratio precedes possibly negative (directional) ratio precedes anharmonic ratio precedes cross-ratio - and see how balance gets variously extended, as with the anharmonic group and the Moebius transformations. And relate that to the Balance as a way of figuring things out.
• In the house of knowledge for mathematics, the three-cycle establishes the substructures for the symmetry group. Similarly, in physics, it establishes the scales for isolating a system (?)
• How does logic come from a quadratic form? Four ways of relating level and metalevel with "and".
• Terrence Tao problem solving

https://books.google.lt/books/about/Solving_Mathematical_Problems_A_Personal.html?id=ZBTJWhXD05MC&redir_esc=y

• Physics is measurement. A single measurement is analysis. Algebra gives the relationships between disparate measurements. But why is the reverse as in the ways of figuring things out in mathematics?
• Ways of discovery in math: Tricki.org. Overview by Timothy Gowers.
• Towards a Periodic Table of Ways of Knowing in the light of metaphors of mathematics Anthony Judge
• Associative composition yields a list (and defines a list). Consider the identity morphism composed with itself.
• Kan extensions are examples of "extending the domain". So consider what they say about the three-cycle in the house of knowledge, how they relate to arguments by continuity and by self-superimposition.

Think of monads as describing models, that is, simplified accounts of a system. Note that monads are built on adjoint functors, which express least upper bounds and greatest lower bounds. So this suggests that the four levels of logic/geometry are related to the four levels of algebra/analysis. But how, perhaps inversely? Because the bounds are third level, but the models are second level. Thus:

• center / induction = variables
• balance-parity / maximum-minimum = working backwards, implication
• sets / bounds = models
• vector spaces / limits = contradictions

What this suggests is that the richest structures are inherently contradictory. But if we pull back to simpler structures then they become safer.

• Relate content and context: Problem -> Contentualize -> Contextualize -> Reformulate problem -> Find relevant categorical requirements -> Solve problem
• House of knowledge: Pushdown automata: Every question has an answer. Their two wings, entering the game and leaving the game, are linked by the three-cycle.
• Trejybės ratas matematikos žinojimo rūmuose. Vis trys nariai susiję su lygtimi X=X. Žr. Curry-Howard-Lambek?
  • apimties išplėtimas - su kategorijų teorija (Kan plėtiniai)
  • tolydumas - su homotipų teorija
  • sekų sulyginimas - su programavimu
• X=X relates the conscious-unbounded (algebra) and the unconscious-bounded (analysis).
• Another way of constructing an equilateral triangle from its side. Build it in a cube. Given a line segment, construct a square with its diagonal, and then a cube from that square. Then can connect the line segment with two other such diagonals to form the equilateral triangle.
• Matt Parker: Math Mistakes

House of knowledge and divisions of everything

• 0 center, 1 balance, 2 sets (for what exists or not), 3 lists, 4 - limit?, 5 - least upper bound?, 6 - max or min, 7 induction.
• How do the kinds of variables relate to the imagination?
• How do the 24 kinds of variables relate to the 4 circulations?
• How does the three cycle relate the algebraic and analytic wings of math's house of knowledge?
• Attiyah: Limits (singularities, zeroes) exist in the ideal world but not the real world. Thus the house of knowledge for mathematics constructs the ideal world from the real world.
• Pair polytope types to get six ways of structuring mathematics as in the house of knowledge.
• Meta-Meta-Theory Tool MMT as a UniFormal framework. Relevant for structure of knowledge - of modeling world by minicolumn?
• In the house of knowledge for mathematics, the three-cycle consists of extending the domain, arguing by continuity, and self-comparing information. These three activities relate to the construction of an adjunction and how that construction adds one, two, or three perspectives, thus extends a division of everything.
• History of math https://www.amazon.com/Cult-Pythagoras-Math-Myths/dp/0822962705
• There are four ways to consider how a level equals a metalevel.
• Choosing a good notation is done through variables. A good notation distinguishes the relevant origin, balance (units around origin), set, list.
• Equality is self-superposition in threesome. Thus 3 is 5-2. Then extend domain. Continuity (homotopy ?) Defines critical point.
• In the six methods of proof, note that three are prior to system and three are within a system. Compare that with the house of knowledge which also distinguishes between ways of figuring things out that are prior to system and after there is system.
• Colimit (algebra, inner structure) -> division of everything (adjoint string) -> limit (analysis)
• Three-cycle: operation +1 (loopspace...), +2 (induction-restriction-coinduction...), +3 (long exact from short exact by derived functor, snake lemma)
• Vector spaces (lists) are colimits (on the algebra side) and analytic limits are categorical limits (on the analysis side).
• Continuity arguments are common in algebraic topology
• Discovery has to do with focusing attention. Attention can focus on a single sheet, blank sheet. Or it can focus on a series of sheets.
• 4 levels of logic/geometry: A) contradiction - odd orthogonal (no barrier), B) model is closed, a substructure - even orthogonal (preserves orientation), C) backwards - go from final model to ever simpler models, D) variable - relate the levels of models.

In the house of knowledge for mathematics

• Algebraic structure grounds colimits (and sets) and analytic relationships ground limits (and adjoints).
• Are the algebraic structures defined in terms of center, balance, sets, lists of morphisms?
• Are the analytic relationships defined in terms of induction (as in defining composition), maximum-minimum, adjoint, limits of morphisms?
• Continuity arguments include the intermediate value theorem.
• Where in the house of knowledge is setting up the distinction between one and all?
• The axioms of set theory describe the ways of figuring things out in a system. The concepts of category theory describe the ways of figuring things out before there is a system. (Thus in category theory we work with many copies of the same structure, whereas in set theory we work with a single copy.)
• The algebraic wing is in terms of nullsome (center), onesome (balance), twosome (set), threesome (list) and the analytic wing is in terms of foursome (induction), fivesome (maximum-minimum), sixsome (least upper bound - greatest lower bound), sevensome (limit).

In my study of mathematics, and in trying to solve mathematical problems, how could I make use of the house of knowledge for mathematics?

• The twelvefold way (circumstances) relates lists, sets, multisets as occur in the ways of figuring things out.

Axiomatization leads to overcontextualization but opens opportunity for eternal life. Relate to Goedel's theorem.

Example - Tom Munnecke's inverted perspective is like finding the proper "center" or "origin" for solving a math problem.

MathDiscovery

• https://karendcampe.wordpress.com/2023/02/04/february-calendar-problems/

Discovered math is Platonic, nonaxiomatic, and so can be stated vaguely, so long as clearly. Invented math is artificial and so must be stated precisely, rigorously, axiomatically. Ways of figuring things out are the ways of discovery. The way that math unfolds is the way of invention. Thus I want to relate discovery and invention.

Math discovery

• Geometry/Logic levels explain how many sheets/origins are involved: 0, 1, 2 or 3
• Rotation is total symmetry. That is why it is the basis for geometry and Lie groups.
• Lie groups show how rotations can be connected together - and how many rotations can be involved in the linking.
• The three-cycle relates algebraic symmetry (the circle) and analytic symmetry {$e^{i\theta}$}.
• Another example of algebraic symmetry ({$i$}) - analytic symmetry (sin or cos) - shows the significance of the square (90 degrees) as for the special orthogonal groups.
• Algebraically-analytically how does it work for the symplectic groups and rotations in the quaternions?
• For what values n do we have analytic symmetry {$f^{(n)}(x)=f(x)$} ?
• Algebra is thinking step-by-step and so it exhibits finiteness. Analysis is discovering the boundaries between steps and so exhibits continuity by discovering the critical points, as in Moore's theory. Healthy irony (verbalization) codes the analogue signal (the emotional tension between expression and meaning) into a discrete alphabet (of boxes organized in a cognitive network).
• How is gravity related to the argument by continuity?
• https://www.masterclass.com/classes/terence-tao-teaches-mathematical-thinking
• Independent trials are the basis for independence of variables and thus randomness. This randomness, this independence is the original implicit context. We can always start over with a new sheet of paper. And that fact manifests itself either as a blank piece of paper (which we work on further) or as a sequence of papers (which we refine).
• The final context is what we can have by letting go of the assumptions that we have taken up. We can take up a new implicit context.
• Our ability to make assumptions and let them go is what allows for symmetry groups. They make context explicit.
• Does the gradation of mathematical proofs match with the six pairs of levels in the system within the 24 ways of figuring things out in mathematics?

The house of knowledge for mathematics describes 4 representations (properties) of everything (onesome, totality), which through their unity establish, define space as algebraic, consisting of enumerated dimensions:

• center (nullsome)
• balance
• set of roots of a polynomial
• list of basis vectors

(Relate this to the binomial theorem.) And it describes 4 representation of the nullsome (center), which through their unity establish, define a point as analytic. This describes four choices:

• induction (adding a vertex, converting the center to a vertex, recursively)
• max or min (adding an axis, as with cross polytopes)
• least upper or greatest lower bound (making a division, a separation on one side or the other)
• limit (center?)

4 levels of knowledge is sufficient (in the chain complexes). The house of knowledge describes those 4 levels. It relates the analytical view of a point with the algebraic view of a space. Consider the Zig Zag Lemma as applying the three-cycle to set up four levels of knowledge, 4 x 3 = 12 circumstances.

Matematikos žinojimo rūmų sparnus sieja

• algebra veda iš centro į sąrašą
• analizė vedą iš sąrašo (indukcijos) į centrą (limitą)

Apsikeičia - ar tai padalinimų ratas? Kiekviename sparne požiūriai prisideda +0, +1, +2, +3.