- MathNotebook
- MathConcepts
- StudyMath
- Geometry
- Logic
- Bott periodicity
- CategoryTheory
- FieldWithOneElement
- MathDiscovery
- Math Connections
Epistemology
- m a t h 4 w i s d o m - g m a i l
- +370 607 27 665
- My work is in the Public Domain for all to share freely.
- 读物 书 影片 维基百科
Introduction E9F5FC
Questions FFFFC0
Software
Geometry problems, Geometry theorems, Geometries, Four geometries, Six transformations, Geometry illustrations, Universal hyperbolic geometry, Triangle geometry, Algebraic geometry, Algebraic topology, Lie theory
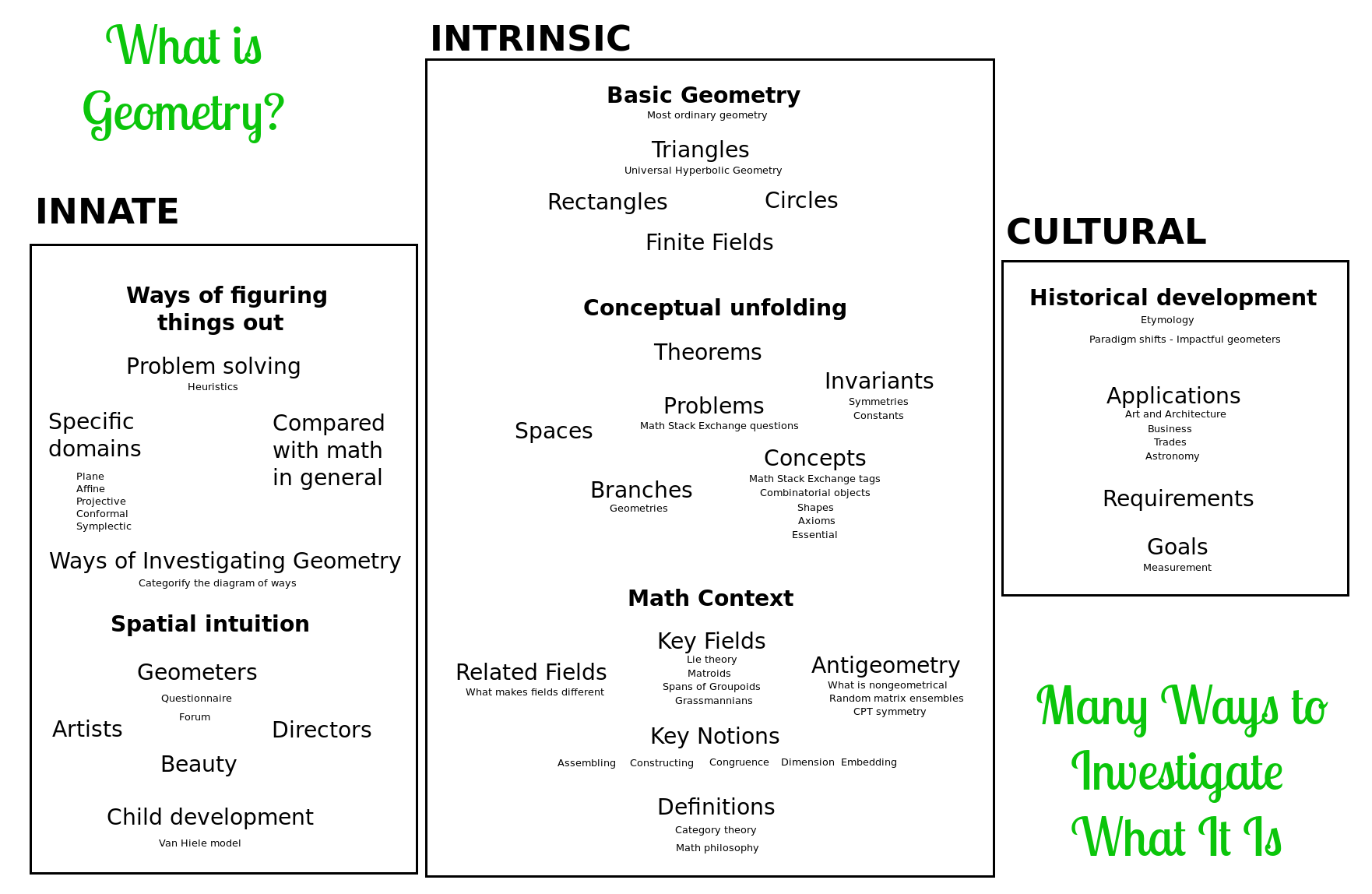
What is geometry?
In what sense, if any, are there four basic geometries: affine, projective, conformal, symplectic?
Overall goals:
- To explain what is geometry.
- To understand what geometry contributes to the overall map of mathematics.
- To distinguish four geometries: affine, projective, conformal and symplectic.
- To understand the relationship between geometries and logic, the classical Lie groups/algebras, category theory, etc.
- To have a better understanding of mathematical concepts, tools, theorems and examples that would serve me in understanding all branches of mathematics.
Motivations:
- Map of branches of mathematics
- Ways of figuring things out in mathematics.
- Keturių klasikinių Lie grupių ir algebrų kombinatorinės ištakos
- Overviewing Bott periodicity
- A Geometry of Moods: Evoked by Wujue Poems of the Tang Dynasty
| 几何 | Jǐhé געאָמעטרי |
Investigations: What is geometry?
Cultural grounds
- Consider the semiotics of signs and symbols, which may be geometrically simple or complex. How is meaning ascribed to specified arrangements of shapes, colors, fonts, brush strokes?
- Consider how other civilizations, in various times and places, have thought of geometry or related disciplines.
- Consider the logic by which alien cultures could include color, time, font, style, calligraphy, symbols, hieroglyphs in geometry or not.
- Consider the development of geometry historically, the significance of key concepts.
- Consider the etymology of geometrical terms in various languages such as Greek, Latin and Chinese.
- Survey applications of geometry.
- Consider the goals of geometry.
- Consider what geometry needs to be so that the goals of geometry could be achieved.
Innate grounds
- Study spatial intuition
- Engage participants at forums for geometers. (ZulipChat)
- Create a questionnaire for geometers to collect their intuition.
- Interview the blind about their understanding of geometry and space.
- Study how artists think of space.
- Study how directors think of space and staging and blocking.
- Study what ordinary people and geometers consider beautiful in geometry.
- Consider how notions of geometry grow during childhood development.
- Study the Van Hiele model
- Systematize the ways of figuring things out in geometry.
- Characterize the observer of geometry.
- Systematize the ways of investigating the foundations of geometry.
Intrinsic grounds
- Consider geometry in the wider context of mathematics.
- Overview definitions and foundations of geometry.
- Consider geometry from the point of view of category theory.
- Consider the philosophy of geometry and the questions that it pursues.
- Consider the branches of geometry in the broader context of the branches of mathematics, especially, how geometry relates algebra, analysis, logic and combinatorics.
- Consider how adding, changing or removing a notion takes us from the most ordinary geometry to variants and other branches of math.
- Consider what is antigeometry, for example, maximally nonuniform choice or non choice.
- Study random matrix ensembles and how they ground CPT symmetry.
- Overview definitions and foundations of geometry.
- Systematize concepts in geometry.
- Characterize what it means for concepts to be essential.
- Analyze the geometry related tags at Math Stack Exchange.
- Analyze geometry in terms of geometrical spaces.
- Analyze geometry in terms of invariants and geometric invariant theory.
- Analyze geometry in terms of symmetries.
- Analyze geometry in terms of axioms: Euclid's, Birkhoff's, Hilbert's, Tarski's
- Analyze geometry in terms of important constants.
- Analyze combinatorial geometry in terms of basic combinatorial objects.
- Analyze geometry in terms of the classification of shapes.
- Systematize geometry theorems, and especially the major theorems, in terms of branches of geometry and sophistication of concepts.
- Systematize branches of geometry.
- Systematize geometry problems including for affine, projective, conformal and symplectic geometry.
- Study the questions about geometry asked at MathStackExchange and MathOverFlow.
- Consider what notions are common to all geometries.
- Consider comprehensively a portion of geometry, especially basic geometry.
- Systematize triangle geometry in terms of centers, problems, concepts, theorems, constructions, how they unfold.
- Consider the six transformations and how they act on {$0, 1, \infty$}.
- Systematize the geometry of circles.
- Systematize the geometry of rectangles.
- Systematize Universal hyperbolic geometry.
- Consider geometry over finite fields, how that relates to choice and the binomial theorem, and how that gets extended to continuous fields and the role of the Grassmannian.
- Consider the geometry of the mythical finite field with one element {$F_1$}.
- Consider the significance of Lie theory in geometry.
- Consider what is the most ordinary geometry that other variants and disciplines build on.
- Systematize triangle geometry in terms of centers, problems, concepts, theorems, constructions, how they unfold.
Epistemology
- How is geometry (and the house of knowledge) related to the fivesome?
Rings
- Why are rings important for geometry rather than just groups?
Topos
- "Grothendieck thought about this very hard and invented his concept of topos, which is roughly a category that serves as a place in which one can do mathematics." A place for figuring things out? What would that mean? Ways of extending the mind by leveraging basic ways of figuring things out and organizing them around a particular observer? The axiomatic system (4 levels, 6 pairs) in which axiomatic math is done?
Curvature
- Does the inside of a sphere have negative curvature, and the outside of sphere have positive curvature? And likewise the inside and outside of a torus?
- Why is negative curvature - the curvature inside - more prominent than positive curvature - the outside of a space?
Asymmetry
- Try to understand asymmetric functions, for example, by setting {$q_3^2=0$}.
Space vs. Time
- What does the definition of space (separating local choice and global position) say about time?
What is geometry?
How I would define geometry
Geometry is the uniformity of choice.
- Regularity of choice allows a space as a whole to have properties, for example, translational symmetry becomes possible.
- A choice may be the product of choices, yielding a product of dimensions.
- We have the logic of choice understood specifically, for a point, but also its implications generally, for a space.
- As the choice becomes irregular, the notion of geometry gets lost.
- Geometry, the regularity of choice, is the set up, the preconditions, for symmetry.
- Geometry is the uniformity of choice. Here the notion of choice comes up again. Note the difference between geometry (as a science of spatial measurement) and topology (as a science of spaces). A graph is geometric in that it consists of points which allow for a choice of edges but is not geometric in the sense that the points may allow for different kinds of choices. What is the relationship between geometry and symmetry? and also randomness? and information? Does geometry of itself entail zero information?
Four choice frameworks
- Four choice frameworks determine four basic geometries.
- There are four geometries (affine, projective, conformal, symplectic) and they relate to the relations between coordinate systems (0, 1, 2, 3).
- There are six transformations between four geometries and they relate ways of looking at triangles.
Bundles
- Space arises with bundles, which separate the homogeneous choice, relevant locally, from the position, given globally.
- A geometry (like hyperbolic geometry) allows for a presentation of a bundle, thus a perspective on a perspective (atsitokėjimas - atvaizdas). Compare with: įsijautimas-aplinkybė.
Manifesting logic (existence, universality)
- Geometry relates to logic.
- Geometry along with logic is the interface between algebra and analysis.
- Get a geometry for each of the Dynkin diagrams.
- Four kinds of rigidifying structure: fixed dimension (orthogonal odd extra), distance (orthogonal), angle (unitary), oriented area (symplectic)
- Rigidity is the invariant that gets preserved by group actions.
- Metric establishes distance
- Adding an inner product to a vector space makes it a Euclidean space/Lorentzian space/pseudo-Riemannian vector space, not just linear algebra.
- Smooth structure on manifold does not rigidify it very much and yields differential topology.
- Adding a complex structure yields complex geometry.
- Adding algebraic structure yields algebraic geometry.
- Consider the "forms" that we add, such as a symplectic form.
- Can add a vector bundle with connection. Or a vector bundle metric.
- Less rigidly, one can put a special function (such as a Morse function) on a manifold. This gives homotopy type information. And the critical point structure gives a rigid description of the manifold (how it divides into cells and which points flow to which points along gradients).
- Geometric topology is in the middle, between geometry and topology. It considers the embeddings of one manifold into another. It can distinguish spaces that are homotopy equivalent but not homeomorphic.
- How do we assign this needed structure? Such a local structure could provide a measure of ‘distance’ between points (in the case of a metric structure), or ‘area’ of a surface (as is specified in the case of a symplectic structure, cf. §13.10), or of ‘angle’ between curves (as with the conformal structure of a Riemann surface; see §8.2), etc. In all the examples just referred to, vector-space notions are what are needed to tell us what this local geometry is, the vector space in question being the n-dimensional tangent space {$T_p$} of a typical point p of the manifold M (where we may think of {$T_p$} as the immediate vicinity of {$p$} in {$M$} ‘infinitely stretched out’; see Fig. 12.6). Penrose, Road to Reality, page 293, §14.1.
- Mostow rigidity theorem Hyperbolic manifolds.
Quadratic forms
- Quadratic forms establish a metric for distance, angle, oriented area.
- Quadratic forms are key for geometry. Moebius transformation involves complex numbers and 2 x 2 matrix. Whereas Clifford algebra involves quadratic form - as a lens for perspectives? Think of a linear form (proportion) as a plain sheet of glass, and a quadratic form as a convex and/or concave lens.
- Quadratic forms are a basic nontrivial homogeneous choice.
Constructions
- Each kind of geometry is based on a different tool set for constructions, on different symmetries, and on a different relationship between zero and infinity. And a different way of relating two dimensions.
- Each geometry is the action of a monoid, thus a language. But that monoid may contain an inverse, which distinguishes the projective geometry from the affine geometry.
- In a free monoid the theorems are equations and they are determined by what can be done with associativity. This is first order logic. A second order logic or higher order logic would be given by what can be expressed, for example, by counting various possibilities.
- Abstract incidence geometries (Axiomatic projective geometry being an example). (Suggested by Todd Trimble).
- They can be considered in various ways as hypergraphs (in graph theory) and block designs (in combinatorial design theory). Matroids are downward-closed hypergraphs (abstract simplicial complexes) with the augmentation property.
Congruence
- At its roots, geometry consists of a notion of congruence between different objects in a space. In the late 19th century, notions of congruence were typically supplied by the action of a Lie group on space. Lie groups generally act quite rigidly, and so a Cartan geometry is a generalization of this notion of congruence to allow for curvature to be present. The flat Cartan geometries — those with zero curvature — are locally equivalent to homogeneous spaces, hence geometries in the sense of Klein.
Symmetries, equivalences, invariant
- Geometry is about symmetries - the Erlangen program.
 Clifford-Klein form Wilhelm Killing thought that for free mobility of rigid bodies there are four spaces: Euclidean, hyperbolic, elliptic and spherical.
Clifford-Klein form Wilhelm Killing thought that for free mobility of rigid bodies there are four spaces: Euclidean, hyperbolic, elliptic and spherical.
- Felix Klein's Erlangen program whereby we consider transformation groups which leave geometric properties invariant
- Felix Klein, Erlangen program
- Lie groups play an enormous role in modern geometry, on several different levels. Felix Klein argued in his Erlangen program that one can consider various "geometries" by specifying an appropriate transformation group that leaves certain geometric properties invariant. Thus Euclidean geometry corresponds to the choice of the group E(3) of distance-preserving transformations of the Euclidean space R3, conformal geometry corresponds to enlarging the group to the conformal group, whereas in projective geometry one is interested in the properties invariant under the projective group. This idea later led to the notion of a G-structure, where G is a Lie group of "local" symmetries of a manifold.
- nLab: Klein geometry is homogeneous space (coset space) {$G/H$} in the context of differential geometry.
- A Klein geometry is a pair {$(G,H)$} where G is a Lie group and H is a closed Lie subgroup of G such that the (left) coset space {$X≔G/H$} is connected. G acts transitively on the homogeneous space X.
- Klein geometries form the local models for Cartan geometries.
 space form
space form
 Killing-Hopf theorem and curvature: hyperbolic space, Euclidean space, n-dimensional sphere. Discrete groups of isometries. Reduction to generalized crystallography.
Killing-Hopf theorem and curvature: hyperbolic space, Euclidean space, n-dimensional sphere. Discrete groups of isometries. Reduction to generalized crystallography.
- nLab: Cartan geometry Cartan geometry is geometry of spaces that are locally (infinitesimally, tangentially) like coset spaces G/H, i.e. like Klein geometries. Intuitively, Cartan geometry studies the geometry of a manifold by ‘rolling without sliding’ the ‘model geometry’ G/H along it. Hence Cartan geometry may be thought of as the globalization of the program of Klein geometry initiated in the Erlangen program.
- A Cartan geometry is defined by principal connection data (hence by cocycles in nonabelian differential cohomology) this means that it serves to express all these kinds of geometries in connection data.
- Cartan connection
- nLab: Principal connection Connection on a principal bundle.
- nLab: Principal bundle
- nLab: Bundle
- moving frames
- Ehresmann connection.
- Geometry is about defining equivalence (of shapes), thus the transformations that maintain equivalence, and the symmetries of those transformations.
- Geometry is about invariants, thus inner products.
- Chromogeometry - Norman Wildberger - the relationship between groups of symmetries, as given by the relationship between inner products
- A quadratic subject, with quadratic concepts: quadrance and spread. (Norman Wildberger)
Figures
- Shape, size, relative position of figures
- Wikipedia defines geometry as "concerned with questions of shape, size, relative position of figures, and the properties of space".
- MathWorld defines geometry as "the study of figures in a space of a given number of dimensions and of a given type", and formally, as "a complete locally homogeneous Riemannian manifold".
- groupoidification and geometric representation
- A groupoid is a category with inverses. It is like a set with symmetries. Vector spaces can be thought in terms of groupoids and linear operators in terms of spans of groupoids. Incidence geometry, including projective geometry, has figures and incidence relations involving them. Spans of groupoids define "invariant witnessed relations" which are the essence of incidence geometry.
- Groupoidification generalize facts from linear algebra as facts about incidence geometry.
- Every Dynkin diagram gives rise to a flavor of incidence geometry, for example, {$A_3$} relates points, lines and planes.
Linking dimensions (choices)
- Geometry is about rotations as the links between dimensions.
- In linking dimensions, the ways of relating the duality of counting forwards and counting backwards.
- Geometries show how to relate (ever more tightly) two distinct dimensions.
Curvature - inversion of rotation
- Geometry is the study of curvature (Atiyah's video talk on Geometry in 2, 3 and 4 dimensions. Intrinsic and extrinsic curvature. Sphere has constant curvature. Sphere - positive - genus 0. Torus (cylinder) - zero curvature - genus 1. Higher genus - negative curvature.
- 2 dimensions - Scalar curvature R
- 3 dimensions - Ricci curvature {$R_{ij}$}
- 4 dimensions - Riemann curvature {$R_{ijk}$}
Embedding spaces
- how to embed a lower dimensional space into a higher dimensional space
- choice relates a space with a subspace that is one dimension less
- Grassmannians
- Tits buildings, symmetric spaces
- how to expand our vision (from a smaller space to a larger space) (Tadashi Tokieda)
Geometry is the way of fitting a lower dimensional vector space into a higher dimensional vector space.
- Tensors give the embedding of a lower dimension into a higher dimension. Taip pat tensoriai sieja erdvę ir jos papildinį, kaip kad gyvybę ir meilę. Tai vyksta vektoriais (tangent space) ir kovektoriais (normal space?) Tad geometrijos pagrindas būtų Tensors over a ring. Kovektoriai išsako idealią bazę. Tensorius susidaro iš kovektorių ir kokovektorių. Ir tie, ir tie yra tiesiniai funkcionalai. Tikai baigtinių dimensijų vektorių erdvėse kokovektoriai tolygūs vektoriams.
- Dflags explain how to fit a lower dimensional vector space into a higher dimensional vector space.
- A geometric embedding is the right notion of embedding or inclusion of topoi F↪E F \hookrightarrow E, i.e. of subtoposes. Notably the inclusion Sh(S)↪PSh(S) Sh(S) \hookrightarrow P of a category of sheaves into its presheaf topos or more generally the inclusion ShjE↪E Sh_j E \hookrightarrow E of sheaves in a topos E E into E E itself, is a geometric embedding. Actually every geometric embedding is of this form, up to equivalence of topoi. Another perspective is that a geometric embedding F↪E F \hookrightarrow E is the localizations of E E at the class W W or morphisms that the left adjoint E→F E \to F sends to isomorphisms in F F.
Dimension
- Notions of dimension d (Mathematical Companion):
- locally looks like d-dimensional space
- the barrier between any two points is never more than d-1 dimensional
- can be covered with sets such that no more than d+1 of them ever overlap
- the largest d such that there is a nontrivial map from a d-dimensional manifold to a substructure of the space
- the sum of dth powers of the diameter of squares that cover the object, with d such that the sum is between zero and
Relating spaces
- the relationship between two spaces, for example, points, lines, planes
Relating expectations
- establishing the boundary between self and world, and transformations of that boundary
- the ways that our expectations can be related, thus how we are related to each other
- the relationship between our old and new search. And search is triggered by constancy, which is the representation of the nullsome which is related to anything and thus to calm and expectations, space and time, etc.
Vector space foundations
- the ways that a vector space is grounded
Construction of sets of roots of polynomials
- In mathematics, especially in algebraic geometry and the theory of complex manifolds, coherent sheaves are a class of sheaves closely linked to the geometric properties of the underlying space. The definition of coherent sheaves is made with reference to a sheaf of rings that codifies this geometric information.
- Coherent sheaves can be seen as a generalization of vector bundles. Unlike vector bundles, they form an abelian category, and so they are closed under operations such as taking kernels, images, and cokernels. The quasi-coherent sheaves are a generalization of coherent sheaves and include the locally free sheaves of infinite rank.
- The snake lemma (relevant for the sevensome and the eightfold way) holds on all Abelian categories.
 Sheaf A sheaf is a tool for systematically tracking data (such as sets, abelian groups, rings) attached to the open sets of a topological space and defined locally with regard to them. For example, for each open set, the data could be the ring of continuous functions defined on that open set. Such data are well behaved in that they can be restricted to smaller open sets, and also the data assigned to an open set are equivalent to all collections of compatible data assigned to collections of smaller open sets covering the original open set (intuitively, every datum is the sum of its constituent data).
Sheaf A sheaf is a tool for systematically tracking data (such as sets, abelian groups, rings) attached to the open sets of a topological space and defined locally with regard to them. For example, for each open set, the data could be the ring of continuous functions defined on that open set. Such data are well behaved in that they can be restricted to smaller open sets, and also the data assigned to an open set are equivalent to all collections of compatible data assigned to collections of smaller open sets covering the original open set (intuitively, every datum is the sum of its constituent data).
 Ringed space A ringed space {$X,\mathcal{O}_{X}$} is a topological space {$X$} together with a sheaf of rings {$\mathcal{O}_{X}$} on {$X$}. The sheaf {$\mathcal{O}_{X}$} is called the structure sheaf of {$X$}.
Ringed space A ringed space {$X,\mathcal{O}_{X}$} is a topological space {$X$} together with a sheaf of rings {$\mathcal{O}_{X}$} on {$X$}. The sheaf {$\mathcal{O}_{X}$} is called the structure sheaf of {$X$}.
- A ringed space is a family of (commutative) rings parametrized by open subsets of a topological space together with ring homomorphisms that play roles of restrictions. Precisely, it is a topological space equipped with a sheaf of rings called a structure sheaf. It is an abstraction of the concept of the rings of continuous (scalar-valued) functions on open subsets.
- An arbitrary topological space {$X$} can be considered a locally ringed space by taking {$\mathcal{O}_{X}$} to be the sheaf of real-valued (or complex-valued) continuous functions on open subsets of {$X$}. The stalk at a point {$x$} can be thought of as the set of all germs of continuous functions at {$x$}; this is a local ring with the unique maximal ideal consisting of those germs whose value at {$x$} is {$0$}.
- If {$X$} is a manifold with some extra structure, we can also take the sheaf of differentiable, or complex-analytic functions. Both of these give rise to locally ringed spaces.
- A coherent sheaf on a ringed space {$(X,{\mathcal {O}}_{X})$} is a sheaf {$\mathcal {F}$} satisfying the following two properties:
- {$\mathcal {F}$} is of finite type over {$\mathcal{O}_X$}, that is, every point in {$X$} has an open neighborhood {$U$} in {$X$} such that there is a surjective morphism {$ {\mathcal{O}}_{X}^{n}|_{U}\to {\mathcal {F}}|_{U}$} for some natural number {$n$};
- for any open set {$U\subseteq X$}, any natural number {$n$}, and any morphism {$ \varphi :{\mathcal{O}}_{X}^{n}|_{U}\to {\mathcal {F}}|_{U}$} of {$\mathcal{O}_X$}-modules, the kernel of {$\varphi$} is of finite type.
- To every algebraic variety {$V$} one can associate a Grothendieck category {$\operatorname {Qcoh}(V)$}, consisting of the
 quasi-coherent sheaves on {$V$}. This category encodes all the relevant geometric information about {$V$}, and {$V$} can be recovered from {$\operatorname {Qcoh}(V)$} (the Gabriel–Rosenberg reconstruction theorem). This example gives rise to one approach to noncommutative algebraic geometry: the study of "non-commutative varieties" is then nothing but the study of (certain) Grothendieck categories.
quasi-coherent sheaves on {$V$}. This category encodes all the relevant geometric information about {$V$}, and {$V$} can be recovered from {$\operatorname {Qcoh}(V)$} (the Gabriel–Rosenberg reconstruction theorem). This example gives rise to one approach to noncommutative algebraic geometry: the study of "non-commutative varieties" is then nothing but the study of (certain) Grothendieck categories.
- The prototypical example of a Grothendieck category is the category of abelian groups; the abelian group {$\mathbb{Z}$} of integers can serve as a generator.
- More generally, given any ring {$R$} (associative, with {$1$}, but not necessarily commutative), the category {$\operatorname{Mod}(R)$} of all right (or alternatively: left) modules over {$R$} is a Grothendieck category; {$R$} itself can serve as a generator.
- Given a topological space {$X$}, the category of all sheaves of abelian groups on {$X$} is a Grothendieck category.
- Given a ringed space {$(X,{\mathcal{O}}_{X})$}, the category of sheaves of {$O_X$}-modules is a Grothendieck category.
- Given an (affine or projective) algebraic variety {$V$} (or more generally: any scheme), the category {$\operatorname{Qcoh}(V)$} of quasi-coherent sheaves on {$V$} is a Grothendieck category.
- nLab: Locale, nLab:Frame can be pointless
Space and time: What we are left when we remove everything (Kant)
- nLab: geometry
- nLab seems to define geometry as part of an Isbell duality between geometry (presheaves) and algebra (copresheaves) where presheaves (contravariant functors C->Set) and copresheaves (functors on C) are identified with each other and thus glued together (for some category C).
- Isbell duality A general abstract adjunction {$(𝒪⊣Spec):CoPresheaves\overset{𝒪}{\underset{Spec}{⇆}}Presheaves$}
- relates (higher) presheaves with (higher) copresheaves on a given (higher) category C
- interprets presheaves as generalized spaces and copresheaves as generalized quantities modeled on C
- thus the "free construction" left adjoint {$𝒪$} takes us from geometry to algebra and the "forgetful" right adjoint {$Spec$} takes us from algebra to geometry
- relates to Gelfand duality, Stone duality, or the embedding of smooth manifolds into formal duals of R-algebras
- nLab: Space and Quantity Isbell duality
Abstract and concrete
- Geometry is concrete, it is a manifestation. Thus group actions can represent an abstract structure (of actions) in terms of a geometrical space (set, vector space, topological space). And this makes for understanding of the abstract in terms of the concrete.
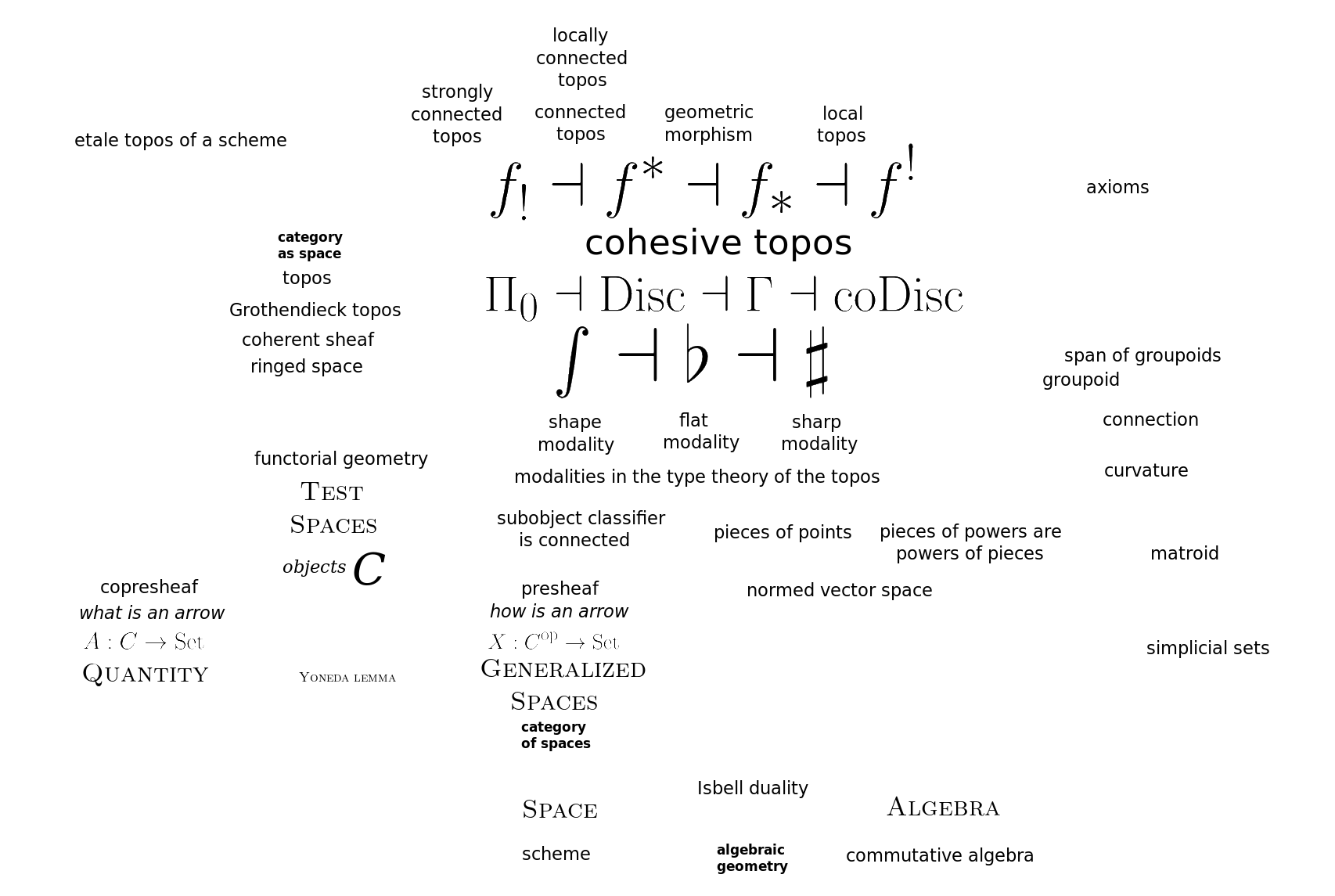
Cohesive topos
- nLab: Modality
- nLab: Cohesive {$(\infty,1)$}-topos
- nLab: Internal modal logic
- Geometric morphism
Schemes
- Ravi Vakil: The intuition for schemes can be built on the intuition for affine complex varieties. Allen Knutson and Terry Tao have pointed out that this involves three different simultaneous generalizations, which can be interpreted as three large themes in mathematics.
- (i) We allow nilpotents in the ring of functions, which is basically analysis (looking at near-solutions of equations instead of exact solutions).
- (ii) We glue these affine schemes together, which is what we do in differential geometry (looking at manifolds instead of coordinate patches).
- (iii) Instead of working over C (or another algebraically closed field), we work more generally over a ring that isn’t an algebraically closed field, or even a field at all, which is basically number theory (solving equations over number fields, rings of integers, etc.).
Properties of space
Spaces of solutions
- Algebraic geometry is the study of spaces of solutions to algebraic equations.
Decisive Abstract General Relations
- Posina Venkata Rayudu. What are Foundations of Geometry and Algebra? Lawvere. "Decisive Abstract General Relations" DAGR
- nLab: Functorial semantics of Algebraic theories
Non-commutative geometry
- Instead of considering the space itself, consider its dual - the space of functions on the space. The corresponding category is in a sense dual to the category of the spaces. Consider commutative algebras of functions (which is the case for ordinary spaces) but also non-commutative algebras (yielding non-commutative geometry).
Spatial intuitions
- Eric Lord Geometry is that in math which is based on our spatial intuitions regarding the real world.
Engaging the Unconscious
- Teasing out notions of location, vantage point, presentation, perspective, figure, invariance.
- Consider how to variously define a circle, a triangle, a line.
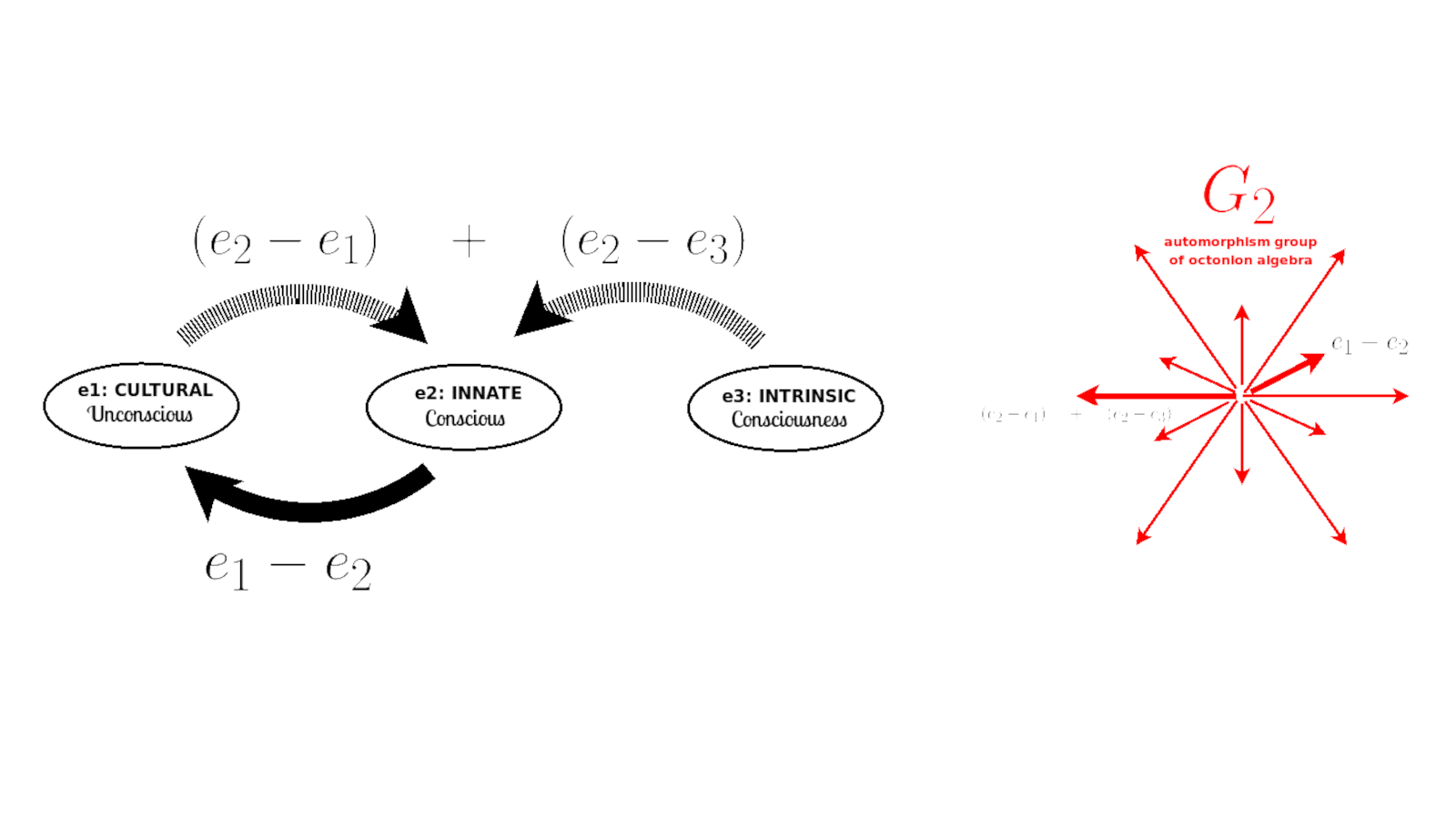
Laying down the requisites for geometry. The purpose is to be able to describe our world view on things in the world. The three minds give the possible world views (+0, +1, +2, +3 perspectives). The world - the available mental states - is given by Bott periodicity.
- Topology establishes position relative to global context.
- Incidence structure establishes location relation to other locations: How to get from one location to another.
- Perspective... Coordinate system... establishes absolute location with regard to a privileged location.
- Geometry establishes the relations between coordinate systems - the rigidity - the cost of travel.
- Geometry is a world view where there can be zero, one, two or three perspectives at play.
Geometry in which space looks the same in all directions: Euclidean, spherical, hyperbolic. Topology, Geometry and Life in Three Dimensions - with Caroline Series.
- Geometric structure means that we can locally have distances and angles that look as if we're locally in the infinite plane, which goes off to infinity.
读物
Sources of information
- List of geometry topics Geometries. Euclidean geometry foundations, 2-dimensional, 3-dimensional, n-dimensional concepts.
Readings about Geometry
 Geometry
Geometry
- Kenneth Brown. Buildings.
- Garret Sobczyk. New Foundations in Mathematics: The Geometric Concept of Number. In this book, I emphasize the development of linear algebra and basic ideas of differential geometry in terms of GA, including the basic concept of the spectral basis. The idea of a spectral basis is what really connects the ideas of a geometric algebra to the traditional approaches to linear algebra and ubiquitous matrices. When GA is properly understood as providing a geometric basis for matrices, the well-established consistency of matrix algebra, in turn, proves the mathematical soundness of GA, without the need to go into more complicated arguments involving tensor analysis and the higher level abstract concepts of advanced mathematics.
- I believe that it is the natural completion of the concept of number to include the concept of direction, and it should be taught that way down into the high school level.
- Garret Sobczyk. The Spectral Basis of a Linear Operator
- Sobczyk. What's in a Pauli matrix?
- Matrix Gateway to Geometric Algebra, Spacetime and Spinors
- Sobczyk. List of publications.
- Includes five transformations! Translation, inversion, dilation, reflection, transversion.
- F.William Lawvere. Taking categories seriously
 Lawvere, What are Foundations of Geometry and Algebra? Functorial Semantics.
Lawvere, What are Foundations of Geometry and Algebra? Functorial Semantics.
- David Corfield: Spatial notions of cohesion as the basis for geometry. A fourfold adjunction: components {$\dashv$} discrete {$\dashv$} points {$\dashv$} codiscrete, and a threefold adjunction of modalities based on that, originally due to Lawvere.
- John Baez about toposes and Lawvere: "In algebraic geometry we are often interested not just in whether or not something is true, but in where it is true." Relate this to scopes: truths about everything, anything, something, nothing.
- What is (a) geometry?
- Muhammad Zubair Ahmad. What is required of a system of mathematical objects and structures to be called a geometry
- Lawvere. Axiomatic Cohesion. Give seven levels as categories grounding geometry:
- I. Categories of space as cohesive backgrounds
- II. Cohesion versus non-cohesion; quality types
- III. Extensive quality; intensive quality in its rarefied and condensed aspects; the canonical qualities form and substance
- IV. Non-cohesion within cohesion via constancy on infinitesimals
- V. The example of reflexive graphs and their atomic numbers
- VI. Sufficient cohesion and the Grothendieck condition
- VII. Weak generation of a subtopos by a quotient topos
- Lawvere. Some Thoughts on the Future of Category Theory
- Lawvere. Cohesive Toposes -- Combinatorial and Infinitesimal Cases
- Lawvere. Lectures on Cohesive Toposes. 2008.
- nLab: Space and Quantity
- Hans Freudenthal. Lie groups in the foundations of geometry.
- Alfred Tarski. What are Logical Notions?
- Todd Trimble. Concrete Groups and Axiomatic Theories I.
- David Corfield. Logic as Invariant Theory Revisited.
- Coxeter. Introduction to geometry.
- Geometry at Cut-the-Knot
- Hilbert. Foundations of Geometry.
- Dubrovin, Fomenko, Novikov. Modern Geometry - Methods and Applications. Part I. The Geometry of Surfaces, Transformation Groups, and Fields.
- Dubrovin, Fomenko, Novikov. Modern Geometry - Methods and Applications. Part II. The Geometry and Topology of Manifolds.
- Dubrovin, Fomenko, Novikov. Modern Geometry - Methods and Applications. Part III. Introduction to Homology Theory.
- John O'Connor
- Sylvain Poirier
- Nickolas Rollick: Algebraic Geometry
- Grothendieck
- Robin Hartshorne, Algebraic Geometry
Sheaves
Schemes
- The Idea of a Scheme
- The Geometry of Schemes, Isenbott and Harris, nicely illustrated concrete examples
Symmetry
- From Summetria to Symmetry: The Making of a Revolutionary Scientific Concept
- Ten symmetries of space time
- Symmetry and the Standard Model Matthew Robinson
- Symmetries and Group Theory in Particle Physics: An Introduction to Space-Time and Internal Symmetries by Giovanni Costa, Gianluigi Fogli
- The Geometry of 3-Manifolds
- Lectures on the Geometric Anatomy of Theoretical Physics
- John Baez. Geometric Representation Theory
Differential Geometry
Noncommutative geometry
- Alain Connes downloads
- Alain Connes: The Music of Shapes
- Alain Connes: Noncommutative Geometry and PhysicsHistory of Geometry
- Audun Holme. Geometry: Our cultural heritage. Online. A good source of examples to think about for math discovery.
- Pierre Cartier: Mad Day's Work: From Grothendieck to Connes and Kontsevich, The Evolution of Concepts of Space and Symmetry
- Berger: Geometry Revealed
- 5000 Years of Geometry: Mathematics in History and Culture] Offers in-depth insights on geometry as a chain of developments in cultural history.
- Audun Holme. A Royal Road to Algebraic Geometry
- Robin Hartshorne Geometry: Euclid and Beyond
- Foundations of geometry
Challenges in Geometry
- Dimension 3: relate Jones quantum invariants (knots, any manifold) with Perlman-Thurston.
- Dimension 4: understand the structure of simply-connected 4-manifolds and the relation to physics.
- Atiyah speculation: Space + Circle = 4 dimensions (Riemannian). Donaldson theory -> geometric models of matter? Signature of 4-manifold = electric charge. Second Betti number = number of protons + neutrons.
Geometry Frameworks
- A topos {$\mathcal{E}$} is cohesive over a base topos {$\mathcal{S}$} if we have an adjoint string {$f_!⊣f^*⊣f_*⊣f!$} where {$f_!,f_*:\mathcal{E}\rightarrow\mathcal{S}$}, {$f^*,f^!:\mathcal{S}\rightarrow\mathcal{E}$} and {$f_!$} preserves finite products.
- Geometric morphism A geometric morphism (and, in the opposite direction, an algebraic morphism) is the adjunction {$f^*⊣f_*$} at the heart of the adjoint string for a cohesive topos.
Isbell duality
Coherent sheaf
Ringed space
Grothendieck topos
Scheme
Span of groupoids
Curvature and connection
Normed vector space
Space and quantity
- From the point of view of the Erlangen program, one may understand that "all points are the same", in the geometry of X. This was true of essentially all geometries proposed before Riemannian geometry, in the middle of the nineteenth century. Thus, for example, Euclidean space, affine space and projective space are all in natural ways homogeneous spaces for their respective symmetry groups. The same is true of the models found of non-Euclidean geometry of constant curvature, such as hyperbolic space.

Important ideas
Notions basic to all geometries
- Euclid's 4 axioms are the trivial notions of the four geometries.
Ring theory
- Rings are important because we want to work with ideals and not subrings, because we are dealing with what is not as well as what is, because we are constructing both top-down and bottom-up.
Noncompact and compact
- Caucher Birkar - noncompact spaces hide information. That is why we work with compact spaces. And why we work with projective spaces.
Thurston's Geometrization conjecture in three dimensions
- Uniformization theorem in two dimensions
My ideas
- Time loop. Inside = outside. Internal. Inside you have apparatus. Infinitely. Not compact.
- Space. Goes from inside to outside by way of perspective that takes you beyond yourself. (Note that going beyond oneself reverses the usual direction of the twosome which leads us from outside to inside. Explain the relationship.)
Ideas
- Fiber is a Zero.
Construction of the continuum
- Start with 0 dimension: a point. Every point is the same point. Then consider embedding a point in 1 dimension. The point does not yet distinguish between the two sides because there is no orientation. A distinction comes with the arisal of a second point. But whether the second point distinguishes the two sides depends on global knowledge. So there must be a third point. This is the relationship between "persons": I, You, Other. Either the dimension is a closed curve or it is an open line. This is "global knowledge". So there is the distinction between local knowledge and global knowledge. But basically geometry is a construction of the continuum, either locally or globally. The construction takes place through infinite sequences, through completion. This completion is not relevant for all constructions.
Basic Geometry
Conics
- Eccentricity defines a conic as the points such that a fixed multiple (the eccentricity) times the distance to a line (directrix) is equal to the distance to a point (focus). The conic is thus a lens (God the Spirit) that relates the line (God the Father) and the point (God the Son). The conic thus relates a higher dimension (the line) with a lower dimension (the point), thus expanding one's perspective. Also, the directrix and focus bring to mind Appolonian polarity.
Polyhedra
- Schematic point of view, or "arithmetics" for regular polyhedra and regular configurations of all sorts.
Circle
- (1 + ti)(1 + ti) = (1 - t2) + (2t) i is the rational parametrization of the circle.
Sphere
- What about the sphere? The stereographic projection of the circle onto the plane in Cartesian coordinates is given by (1 + xi + yj)(1 + xi + yj) where ij + ji = 1, that is, i and j anticommute.
- square-root-of-pi is gamma-of-negative-one-half (relate this to the volume of an odd-dimensional ball: pi-to-the-n/2 over (n/2)!
The eightfold layers of geometry bring to mind the layers of music.
Ask for help and advice
David Michael Roberts. The Higher Geometer. (Mathstodon)
Notes
Frederic Schuller's course, "Lectures on the Geometric Anatomy of Theoretical Physics", starts by previewing eight levels: logic, set theory, topology, topological manifolds, differentiable manifolds, bundles, geometry (symplectic / Lorentzian metric), and on top of that, various subjects in physics (classical mechanics, electromagnetism, quantum mechanics, statistical physics, special / general relativity.
Show that geometry is based on eight levels as organized by Bott periodicity. Then show that this means that the possible geometries are very limited as given by the inner products and the classical Lie groups, which participate in Bott periodicity.
Todd Trimble. Buildings and BN pairs.
Symmetric spaces as the basis for geometry.
- Lavor, Alves. Slides: Distance Geometry and Clifford Algebra
- F. William Lawvere - What is a Space?
- F. William Lawvere - Dialectic of the Continuous and Discrete
Geometry describes things in the world.
Lawvere: Most important topos is the etale topos of a given scheme of a given geometry. In analytic geometry, there is the implicit function theorem and so can talk of homeomorphisms. But this is lacking in algebraic geometry, where the square root is not invertible. But there is an infinitesimal analogue that the derivative at each point, which is a linear transformation, should be invertible.
Why is color not part of geometry? Could it be for another civilization? Or time? Or temperature? Or calligraphy? Hieroglyphics? Semiotics?
What can we say about the symplectic form {$x_1y_2-x_2y_1$}? and how does it relate to symplectic geometry? {$\textrm{Sp}(1,\mathbb{R})=\{A:\mathbb{R}\rightarrow\mathbb{R} | \omega(Ax,Ay)=\omega(x,y) \textrm{ for all } x,y\in\mathbb{R}^2\}$}.
Robin Hartshorne. Algebraic Geometry.
Is p-adic geometry related to fractions and thus the number of bits of information needed to express that?
Could there be four geometries based on the four normed division algebras? Real, complex, quaternion, octonion? and their projective planes? But the symplectic geometry seems based on quaternions. What would octonion geometry mean?
- Geometry arises on a vector space when we place a quadratic form on it, {$Q:V\rightarrow K$}. It gives a notion of length of a vector because {$Q(av)=a^2Q(v)$}, and also a notion of distance because there is a symmetric bilinear form {$B(v,w)=\frac{1}{2}(Q(v+w)-Q(v)-Q(w))$}.
- https://en.wikipedia.org/wiki/Cayley%E2%80%93Klein_metric Are there niine Cayley-Klein geometries?
In choice frameworks, such as the simplex, the center is the basis for geometry and the vertices are the basis for matter. Together can they ground general relativity?
Course: Nonlinear Dynamics. Geometry of Chaos.
John Onstead. One Space to Rule Them All. Thinking through a hierarchy of notions of space.
| O coordinate systems | 1 coordinate system | 2 coordinate systems | 3 coordinate systems |
| fixed dimension | distance | angle | oriented area |
| proof by contradiction | model | implication - working backwards | variables |
Todd Trimble recommended Lawvere on algebraic theories and on hyperdoctrines, helpful for understanding variables.
Mark Ronan. Lectures on Buildings.
Mark Ronan. Symmetry and the Monster.
Geometries may be modding out by different dimensions... projective by a line, conformal by ? symplectic by ?
- https://en.wikipedia.org/wiki/Geometric_probability
- Category theory Zulip chat. What are Categories of Spaces?
- Philosophy Stack Exchange. Can there be a rule of thumb / algorithm to optimize level of generality?
Shoelace formula for oriented area of a polygon
Coxeter. Regular polytopes. Includes prehistory. Boole.
90 degrees + 90 degrees can equal anything. But specifically can go from the diameter of a cube (standing on its vertex) to the vertex and back on the diameter to any point. But the same is true for 120 + 120.
- Mikhail Kapranov. Supergeometry in mathematics and physics. (Conscious) square roots of (unconscious) observables.
- David Corfield. Supergeometry.
- Michael Friedman. Dynamics of Reason.
- David Corfield. Friedman's Dynamics of Reason.
- David Corfield. Homotopification.
1999. I asked God which questions I should think over so as to understand why good will makes way for good heart. He responded:
- What captures attention and guides it? mažėjantis laisvumas
- What drops down upon reality and bounces away in random paths? didėjantis laisvumas
- What is wound in one direction, and lives through spinning in the opposite direction? prasmingas - kodėl
- What falls as rain day and night until there sprout and grow plants that will bear fruit? pastovus - kaip
- What like a ray reflects off of society and does not return? betarpiškas - koks
- What by its turning (in the direction of winding) commands our attention and then slips away to the side? tiesus - ar