• View
• Edit
• History
• Print

KimZeng trees, Research Program Fivesome, Meixner polynomials

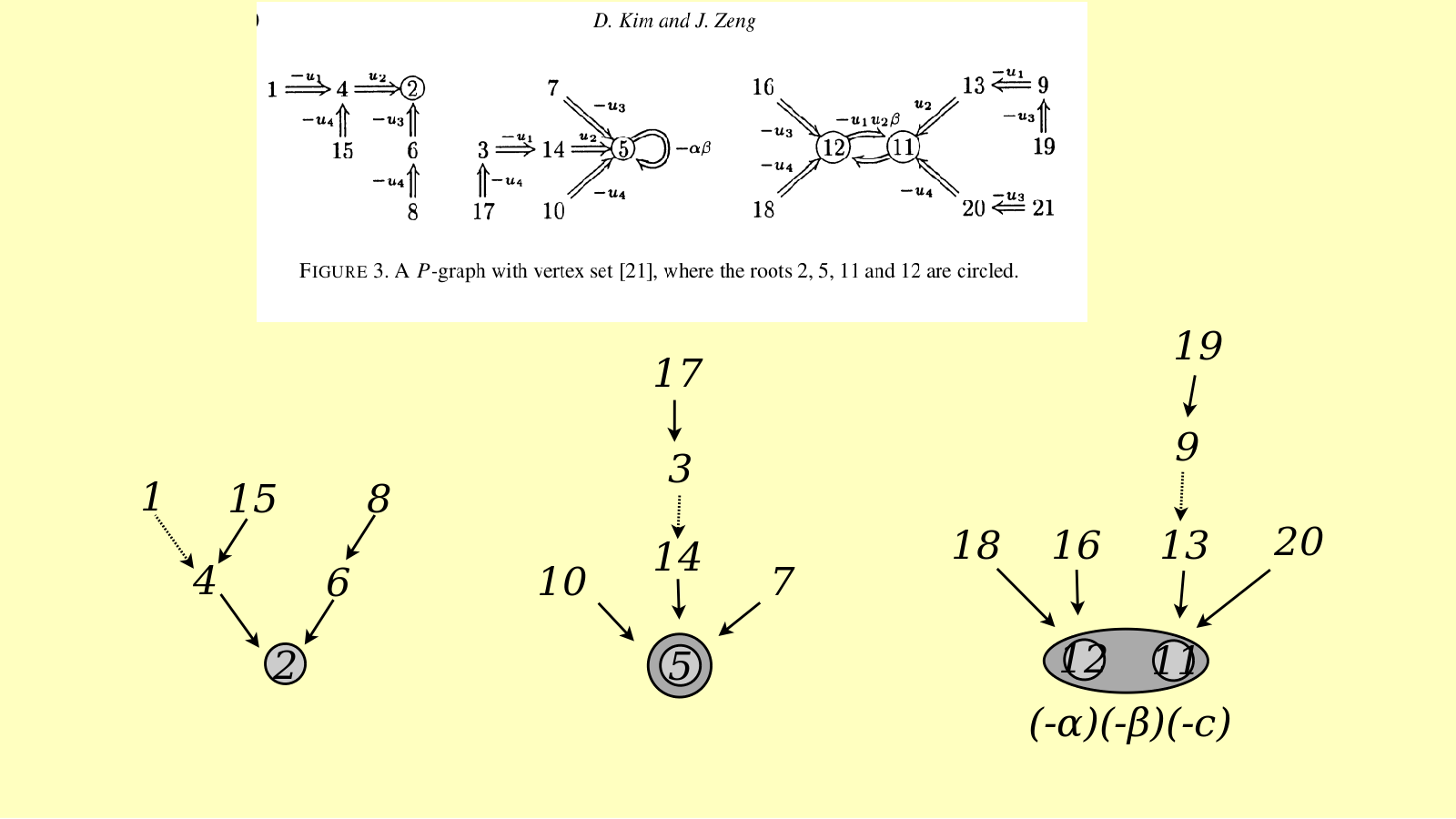
Here is my combinatorial interpretation of the orthogonal Sheffer polynomials. It is based on Kim-Zeng's interpretation, which is a direct reading of the recurrence relation, suitably written out.

This has a basic form of memory. Is it like a pushdown automata, which has sequential memory? Or is it more powerful than that?

Causal tree

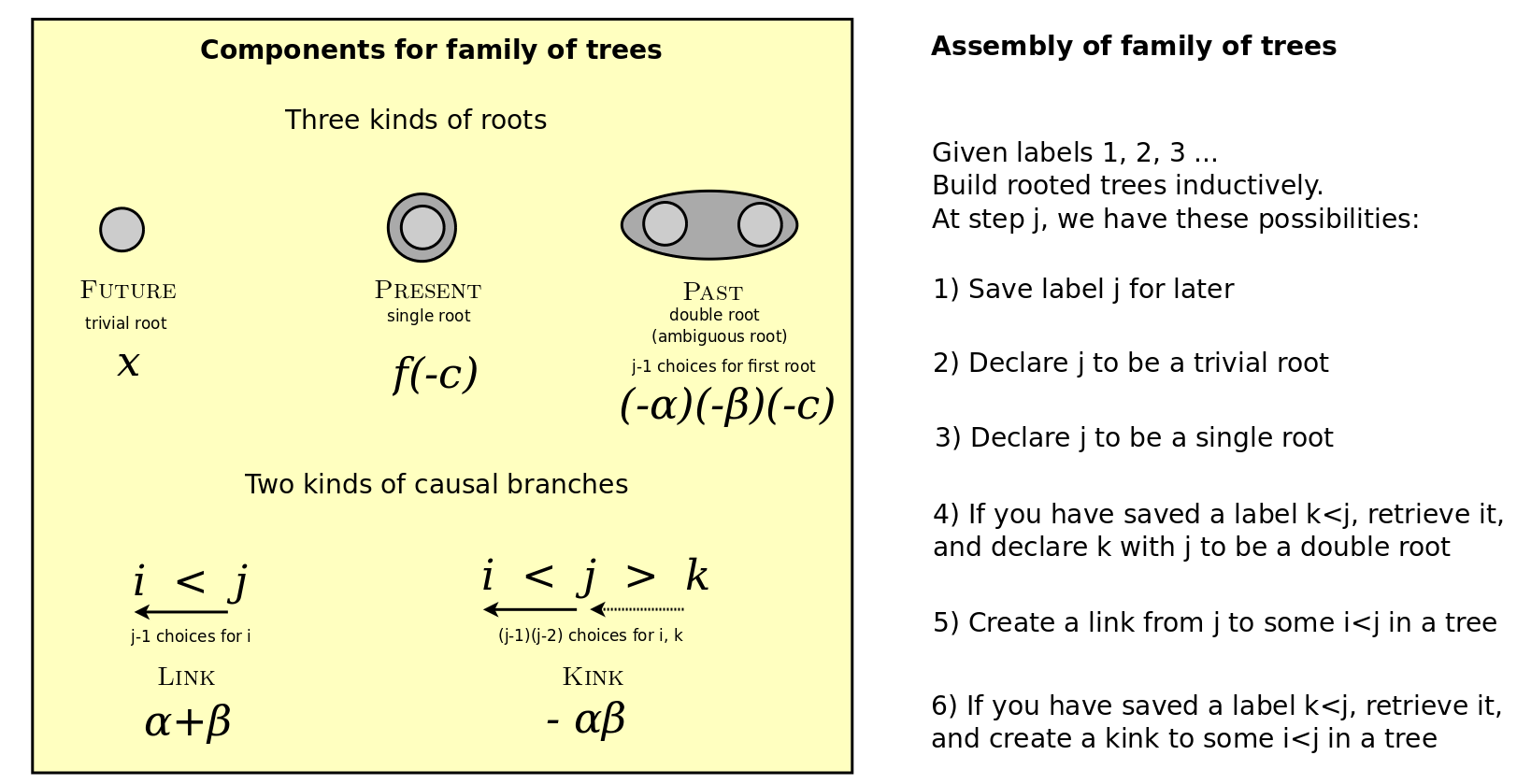
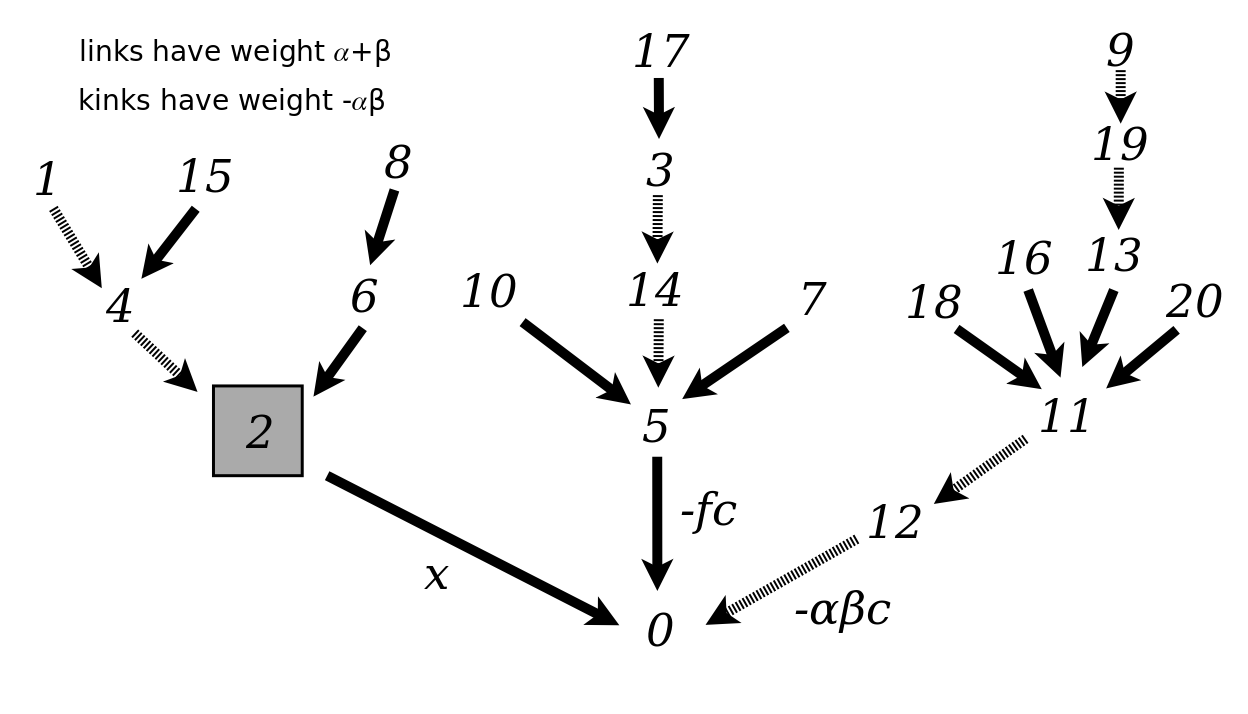
Rather than deal with a family of trees, it may be simpler, and more meaningful, as a growth process, to consider them all as a pointed partition where the parts are causal trees. For this we need to have an initial free space (the root of the tree) that we lay down at the very beginning and that has no weight. Then with each subsequent label we have four choices - we put it down as a link, or put it down as a kink, or save it, or create a new compartment. In the case of a compartment, we may think of it as a potential branch for the main tree, which may become an actual branch upon evaluating the weight {$x$}.

In this way, the trivial roots are compartments, the single roots are links to the main root, and the double roots are kinks to the main root. In this way, we don't need to have the extra condition that the adjacent labels to the single root or double root are not kinks, or that the labels in a double root's tree are all greater than either root.

Thus we have eliminated the different kinds of root, or rather, have the notion of compartment, as we should. We have, as a result, a single causal tree with links and kinks, and with compartments, which is physically more relevant. Indeed, mathematically, this also says that we are starting with {$P_0(x)=1$}.

Compare with pointed partitions

Sheffer Polynomials: Combinatorial Space for Quantum Physics (slides)

Given {$\sum_{n=0}^{\infty}P_n(x)\frac{t^n}{n!} = A(t)e^{xu(t)}$} we have {$n!P_n(x)=\frac{\textrm{d}^n}{\textrm{d}t^n}A(t)e^{xu(t)}\bigg|_{t=0}$} which is the sum of pointed partitions having weights {$A^{(k)}(0)xu^{(l_1)}(0)xu^{(l_2)}(0)\cdots xu^{(l_m)}(0)$} where {$k+l_1+l_2+\dots +l_m = n$}. If we have {$A(t)=1+a_1t + a_2t^2 + a_3t^3+\cdots$} and {$u(t) = t+ u_2t^2 + u_3t^3+\dots$} then the weights are {$k!a_k x^m l_1!u_{l_1}l_2!u_{l_2}\cdots l_m!u_{l_m}$}. And so we have {$n!P_n(x)=\sum_{m=0}^n x^m \sum_{k+l_1+l_2+\cdots +l_m=n}k!l_1!l_2!l_m!a_k u_{l_1}u_{l_2}\cdots u_{l_m}$}. Indeed, {$P_n(x)=\sum_{m=0}^n x^m \sum_{k+l_1+l_2+\cdots +l_m=n}\binom{n}{k,l_1,l_2,\dots, l_m} a_k u_{l_1}u_{l_2}\cdots u_{l_m}$}.

We can now place this into our recurrence relation:

{$P_{n+1}(x)=[x-(((-\alpha)+(-\beta))n+cf)]P_n(x)-(-\alpha)(-\beta)[n(n-1) + nc]P_{n-1}(x)$}

{$\sum_{m=0}^{n+1} x^m \sum_{k+l_1+l_2+\cdots +l_m=n+1}\binom{n+1}{k,l_1,l_2,\dots, l_m} a_k u_{l_1}u_{l_2}\cdots u_{l_m}=$}

{$[x-(((-\alpha)+(-\beta))n+cf)]\sum_{m=0}^n x^m \sum_{k+l_1+l_2+\cdots +l_m=n}\binom{n}{k,l_1,l_2,\dots, l_m} a_k u_{l_1}u_{l_2}\cdots u_{l_m}-(-\alpha)(-\beta)[n(n-1) + nc]\sum_{m=0}^{n-1} x^m \sum_{k+l_1+l_2+\cdots +l_m=n-1}\binom{n-1}{k,l_1,l_2,\dots, l_m} a_k u_{l_1}u_{l_2}\cdots u_{l_m}$}