Math 4 Wisdom. "Mathematics for Wisdom" by Andrius Kulikauskas.

See also my extended abstract for the Applied Category Theory 2023 conference.

The Yoneda Embedding Expresses Whether, What, How, Why

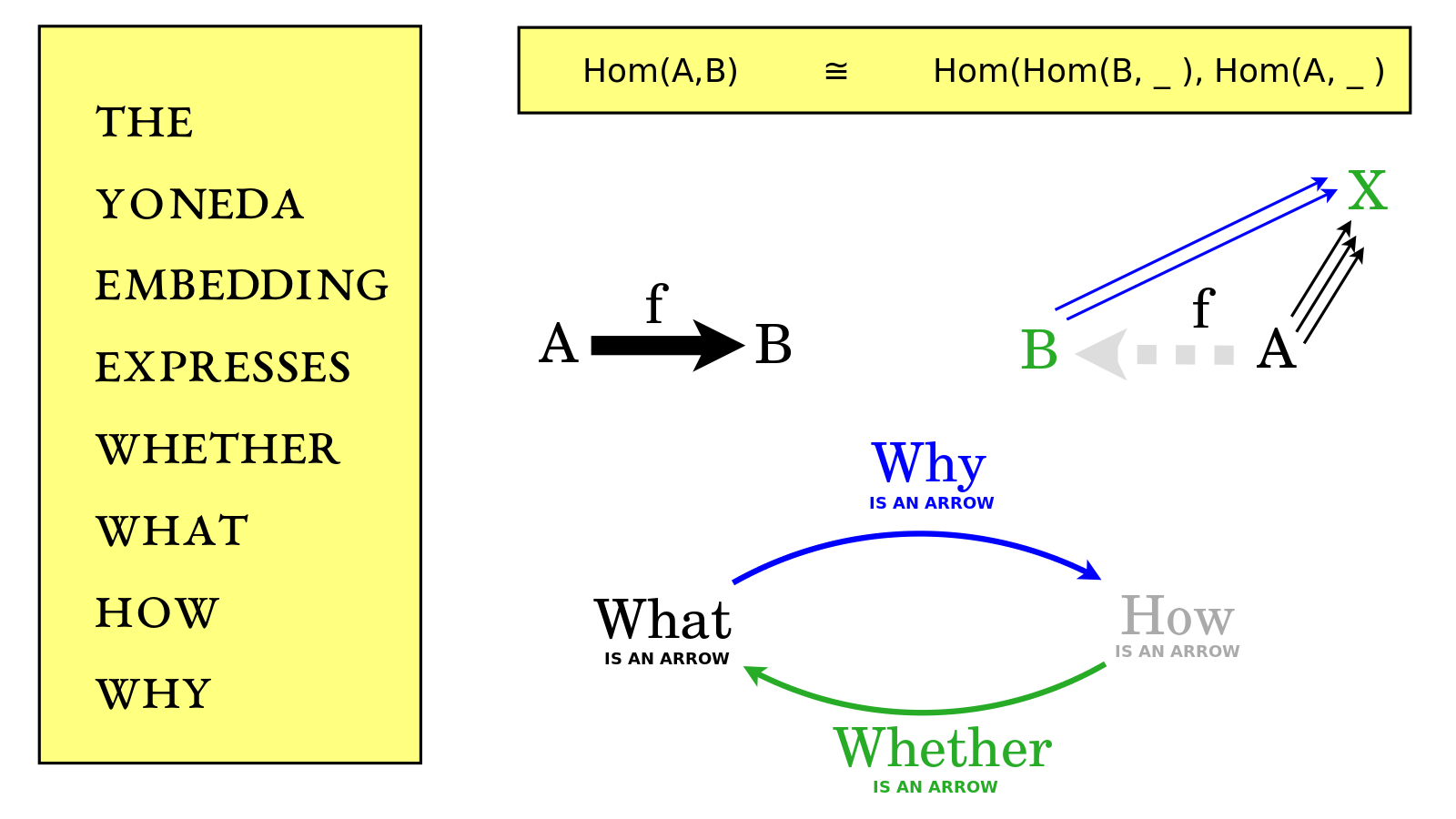
The Yoneda Lemma is the fundamental theorem of category theory. The Yoneda Embedding is the backbone of the Yoneda Lemma. I will show how the Yoneda Embedding relates four levels of knowledge - Whether, What, How, Why - as applied to an arrow f from A to B.

I am Andrius Kulikauskas and this is Math 4 Wisdom.

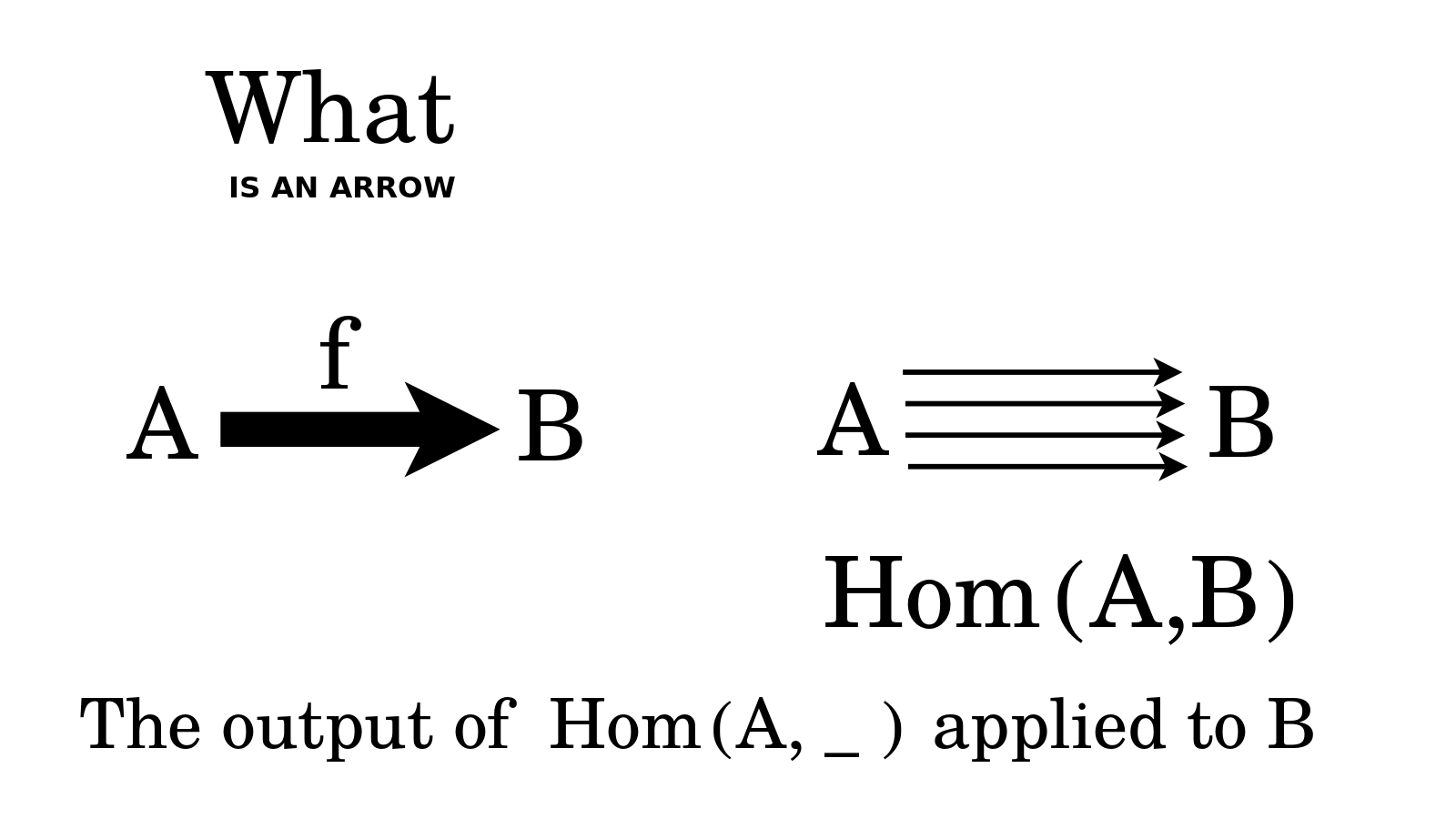
What is an arrow {$f$} from {$A$} to {$B$}? Basically, that is what I have drawn. But specifically, it is an element in the set of arrows that go from {$A$} to {$B$}. We give such a set the name {$\textrm{Hom}(A,B)$} and we call it a homset. {$\textrm{Hom}$} is short for homomorphism since we are typically thinking of {$A$} and {$B$} as being mathematical objects of the same kind, in the same category, such as groups or spaces or graphs, and then the arrows are structure preserving maps, known as morphisms or homomorphisms.

Furthermore, we can think of {$\textrm{Hom}(A, \_ )$} as a function, known as a functor, whose input is an object such as {$B$} and whose output is the set of arrows from {$A$} to {$B$}. We can think of the functor {$\textrm{Hom}(A, \_ )$} as the action of laying down the arrows from a fixed {$A$} to the input {$B$}. In the words of Steve Adowey, "A functor is a picture of one category in another category." Here the functor is taking us from the world of {$A$} and {$B$} to the world of sets, thus picturing what their relationship looks like in the world of sets. What is an arrow {$f$} from {$A$} to {$B$}? It is part of this picture, it is an element in the set of arrows which is outputted.

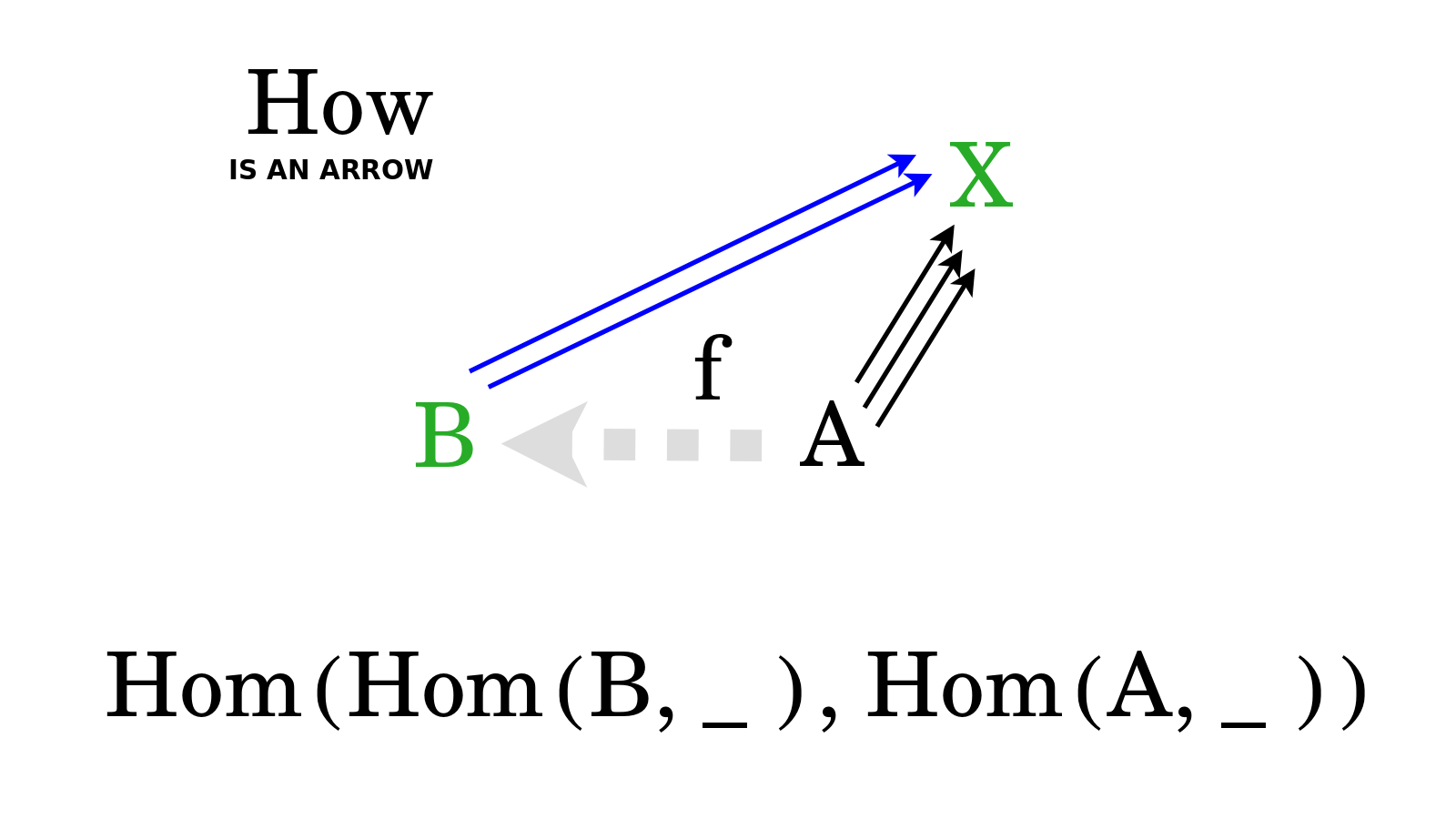
How is an arrow {$f$} from {$A$} to {$B$}? It is the action which prepends this arrow as a puzzle piece that was missing. Consider the arrows from {$B$} to {$X$}. If we prepend the arrow {$f$}, then by composition we will get arrows from {$A$} to {$X$}. We are filling in the arrow that was not, that was lacking, that was missing. In doing so, we are extending the arrows from {$B$} to {$X$} so that they become arrows from {$A$} to {$X$}. Indeed, our action is extending the functor {$\textrm{Hom}(B,\_)$} which lays down arrows from {$B$} to some {$X$}, and that extension yields arrows from {$A$} to that {$X$}, which is what the functor {$\textrm{Hom}(A,\_)$} does. This turns out to be a natural transformation, which is to say, a map, a morphism, an arrow from one functor to another functor. The natural transformation works by filling in the missing arrow with a particular arrow such as {$f$}. The Yoneda lemma says, in this case, that for each arrow {$f$} from {$A$} to {$B$} there is a corresponding natural transformation, and here those are all of the natural transformations, there are no other possible, there are no mysteriously clever natural transformations that could satisfy functoriality, which is to say, act suitably, harmoniously, systematically, within the system of arrows that {$f$} belongs to.

A natural transformation is a functor between functors, an arrow between arrows. In the words of Steve Awodey, "A good way to think of a functor is as a kind of construction." When we think How there is an arrow {$f$} from {$A$} to {$B$}, we think of this arrow as this natural transformation, this action which fills in the gap from {$A$} to {$B$} with a particular arrow {$f$} from {$A$} to {$B$} and thereby extends the elements of the output of the functor {$\textrm{Hom}(B,\_)$} to yield elements in the output of {$\text{Hom}(A,\_)$}. We write these natural transformations {$\textrm{Hom}(\textrm{Hom}(B,\_),\textrm{Hom}(A,\_)$} and note that the order of {$A$} and {$B$} has become reversed because we are prepending the arrow {$f$} to an old arrow from {$B$} to {$X$} to yield a new arrow from {$A$} to {$X$}. How is an arrow {$f$} from {$A$} to {$B$}? It is the natural transformation which places the arrow {$f$} to bridge the gap from {$A$} to {$B$}.

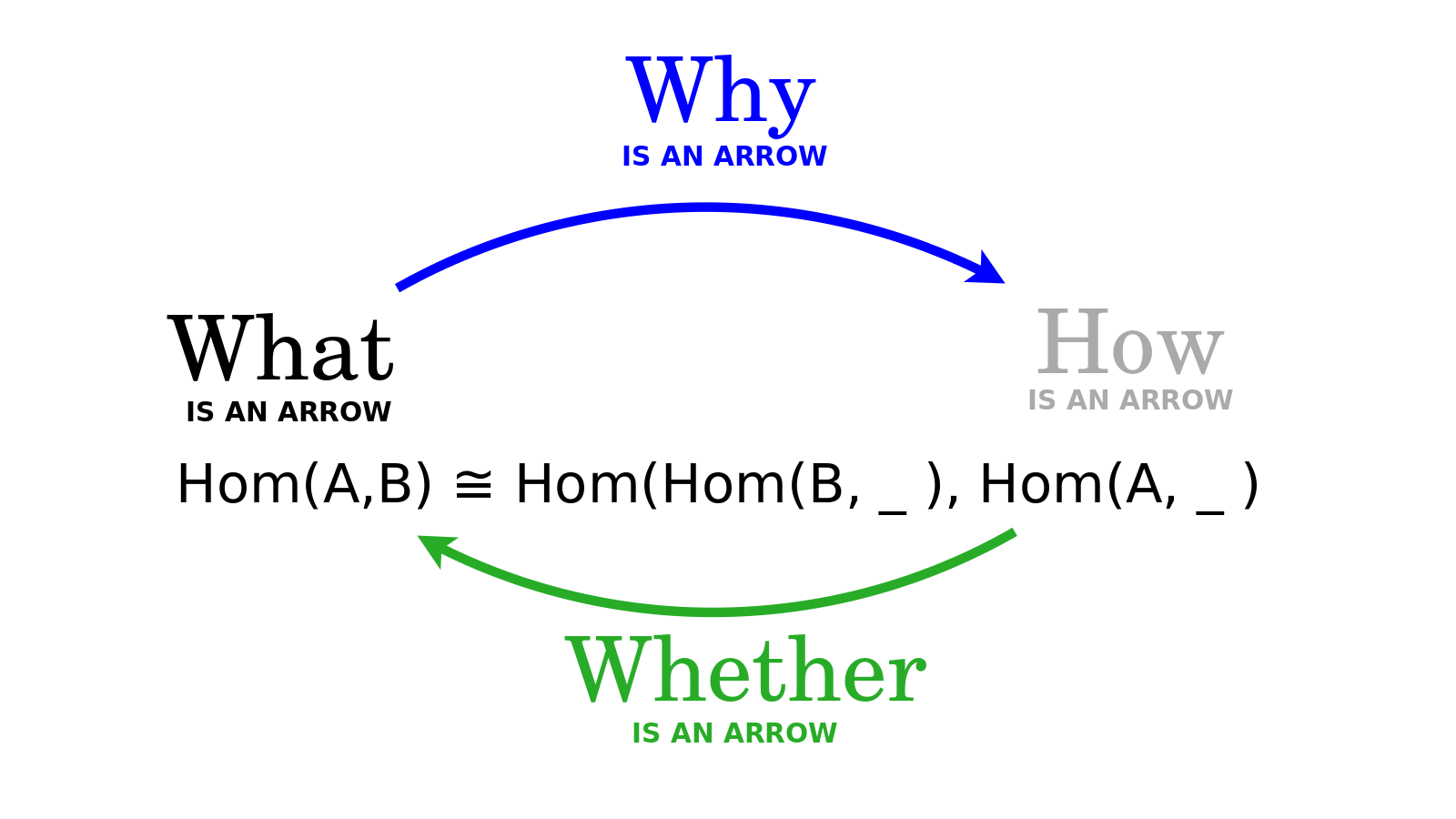
The Yoneda embedding relates What is an arrow {$f$} and How is an arrow {$f$}. The Yoneda embedding sets up a natural isomorphism between these two ways of looking at things. This natural isomorphism consists of two natural transformations. One natural transformation takes us from the world of How to the world of What and thereby describes Whether there is an arrow. The other natural transformation moves us in the opposite direction, from the world of What to the world of How and thereby describes Why there is an arrow. These natural transformations involve functoriality, the assurance that the whole system fits together harmoniously, which I discuss later in this video, but for now I will simply focus on the related bijection between What is an arrow {$f$} and How is an arrow {$f$}. This bijection consists of two set functions, one of which takes us from What to How, and the other one of which takes us from How to What.

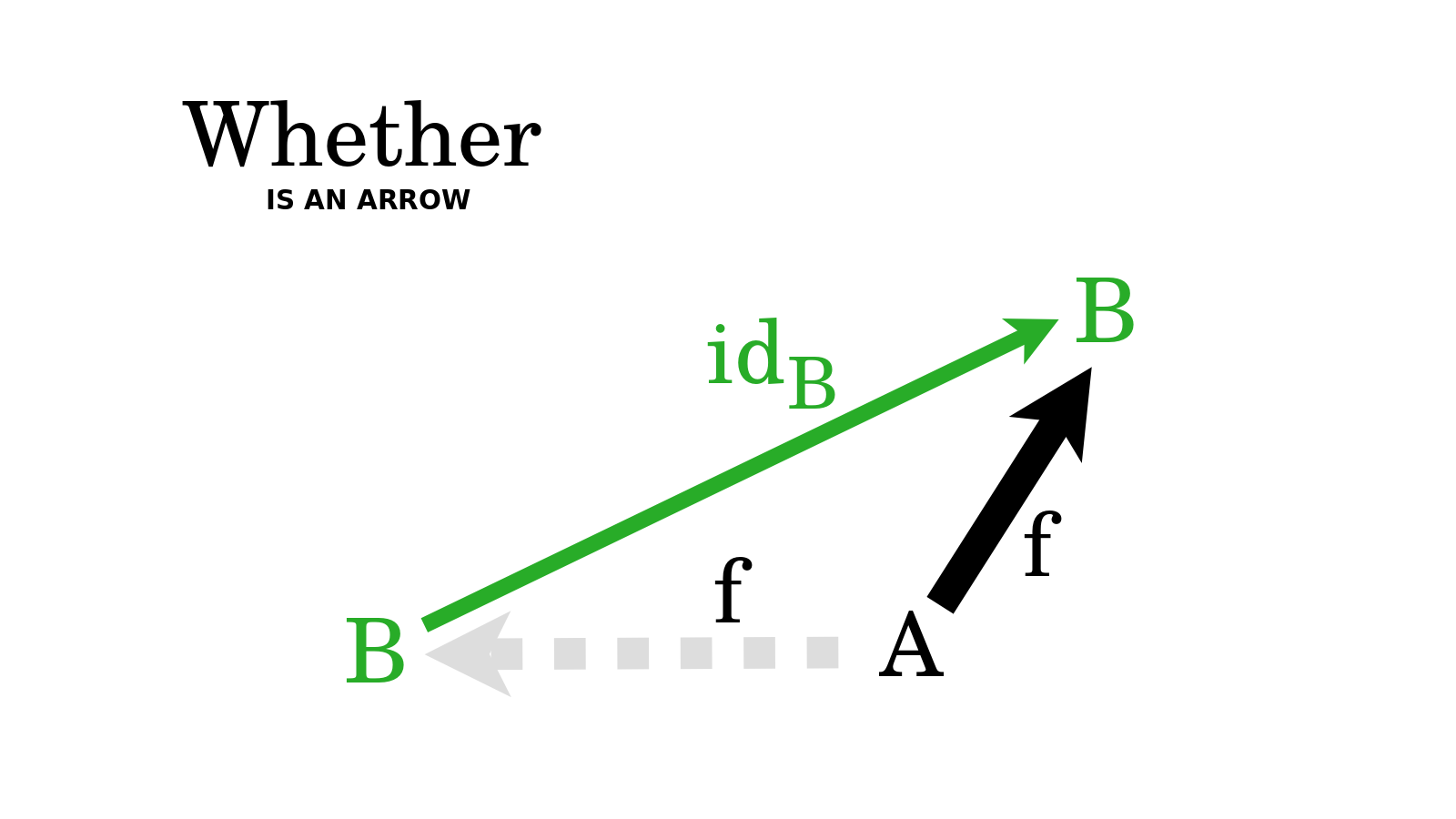
Let us now start with How is an arrow {$f$} from {$A$} to {$B$}. By this I mean that there is a gap from {$A$} to {$B$} and we know how to fill that gap with the arrow {$f$}. And in doing so, we will extend any arrow from {$B$} to {$X$} by prepending {$f$}, yielding an arrow from {$A$} to {$X$}. Here I will cite what Eugenia Cheng, in her new book "The Joy of Abstraction", calls "The Yoneda-ey principle". She says, "the one thing we know we have in any world of homsets is the identity, and all the Yoneda functors and natural transformations are acting by composition on one side or the other." For us this means, let us consider the case when {$X=B$}, and specifically, the identity morphism from {$B$} to {$B$}, in other words, the do-nothing action on {$B$}, which does nothing to {$B$} but just keeps it the way it is. Then the action How prepends to it the arrow {$f$} and this yields that very same arrow {$f$}, which is What {$f$} is. Thus the trivial extention of {$f$}, the do-nothing action from {$B$} to {$B$}, this existential stub, is the grounds Whether there is an arrow {$f$}. It is the aspect, the feature, the essence, by which the action How yields the arrow What. Whether is what takes us from How to What.

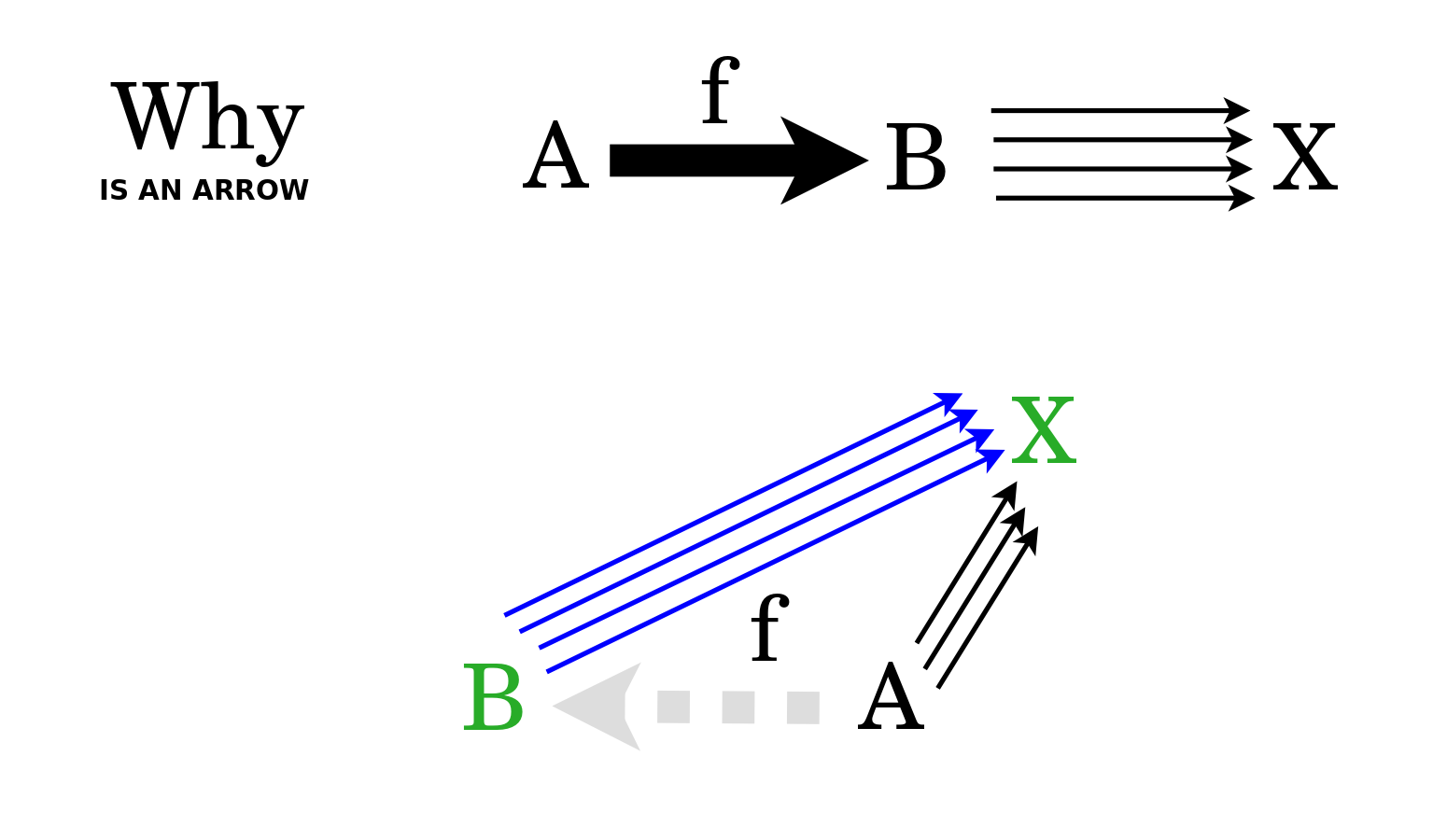
In the other direction, let us start with What is an arrow {$f$} from {$A$} to {$B$}. And let us consider all of the arrows that pass through it, from {$A$} through {$B$} to {$X$}, where {$X$} may be any object. Note that these are all arrows from {$A$} to {$X$}. Here I will cite Tai-Danae Bradley's blog post "The Yoneda perspective". She says, "Mathematical objects are completely determined by their relationships to other objects." In other words, you can judge a person by the company they keep. But let us focus not on objects, but rather the arrows. The reason Why there is an arrow {$f$} from {$A$} to {$B$} is that this is the action we can extract from that collection of all of the arrows which pass through on their way to some {$X$}. It is the action of prepending {$f$} to each input arrow {$B$} to {$X$}. That extraction is the essence of the arrow {$f$}, it is the reason Why it exists within the entire, harmonious system of arrows. Thus Why takes us from What is the arrow {$f$} to the action How is the arrow {$f$}.

In summary, we've conceived the Yoneda Embedding in terms of four levels of knowledge: Whether, What, How, Why. We can appreciate why there are four understandings. What and How give us two different ways of looking at arrows. What shows that the arrow is. How shows that the arrow is not and so we can place it where it is not. It make sense that, as regards our experience, How precedes What. In our experience, we fill in the missing arrows and then we have them. We experience the gaining of knowledge but not the losing of it. Even in cases where we realize that we were mistaken, we are gaining knowledge. However, mathematically, it is the same whether we add an arrow or remove it.

What and How refer to possibilities within sets in the familiar world of Sets, which we could say is the world of every day appearances. But underlying that we can have a more fundamental world beneath the appearances, where {$A$} and {$B$} and {$X$} and arrows such as {$f$} reside. The point of the Yoneda Embedding is that this cryptic world can be studied in terms of the world of appearances, which is to say, of sets and set functions, including sets of arrows. The way we do that is, in the world of What, to think of the set of arrows from {$A$} to {$B$}. The Yoneda embedding asserts that this corresponds to sets of natural transformations, the actions How we go from the set of arrows from {$B$} to {$X$} to the set of arrows from {$A$} to {$X$} by prepending {$f$}. Note that in the world of What, the arrow {$f$} goes from a cryptic object {$A$} to a cryptic object {$B$}, but in the world of How, the corresponding action {$f$} goes from a set of arrows to another set of arrows, which is to say, lives completely in the world of arrows. Practically speaking, the cryptic arrow {$f$} gets lifted up into the world of appearances when we think of it actively, in terms of How it functions.

Whether and Why take us back and forth between these two worlds of What and How. Whether and Why both refer to ideal notions in the cryptic world. Whether relies on the do nothing action, which is intrinsically self-contradictory, as when we speak of silence or when we count nothing or when we write of a blank page, for these things are not self-contradictory only if we consider them second hand, at a meta level, and yet here they are considered first hand, on the level. Why relies on the fact that the cryptic world of arrows obeys composition, so that if we have an arrow from {$A$} to {$B$}, and another arrow from {$B$} to {$X$}, then they will necessarily yield some arrow from {$A$} to {$X$}. Why leverages the fact that the system is absolutely harmonious with regard to composition and thus we can extract Why, the action of placing in the arrow {$f$} so that all of the compositions it initiates are harmonious.

This analysis of the Yoneda Embedding in terms of Whether, What, How, Why suggests that these four levels of knowledge do function together as a cognitive framework. All four perspectives have a role to play. They may indeed form a complete set as I claim based on many other examples. However, in this formulation, we could wonder, what would it mean to relate the natural transformations Whether and Why, perhaps with a new pair of arrows?

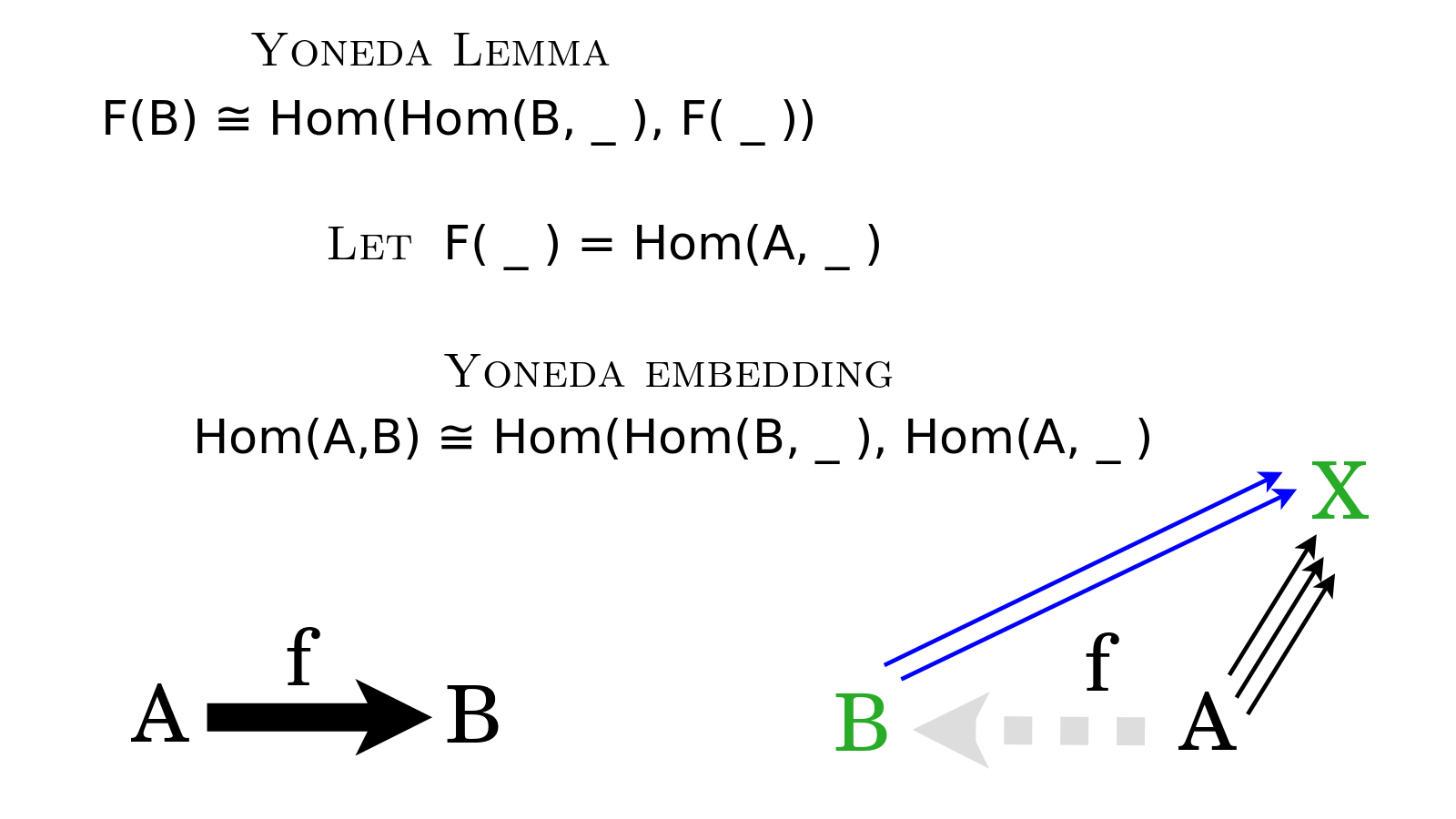
The Yoneda Lemma is a more general version of the Yoneda Embedding. The logic is basically the same but the circumstances are more abstract. Instead of an object {$A$} and a functor {$\textrm{Hom}(A,\_)$}, we think more generally in terms of a functor {$F(\_)$}. Recall that the natural transformations Whether and Why focused on the arrows from {$B$} to {$X$} and from {$B$} to {$B$}, and since those arrows do remain, the logic is practically unchanged. It's just unclear how to draw the diagrams now.

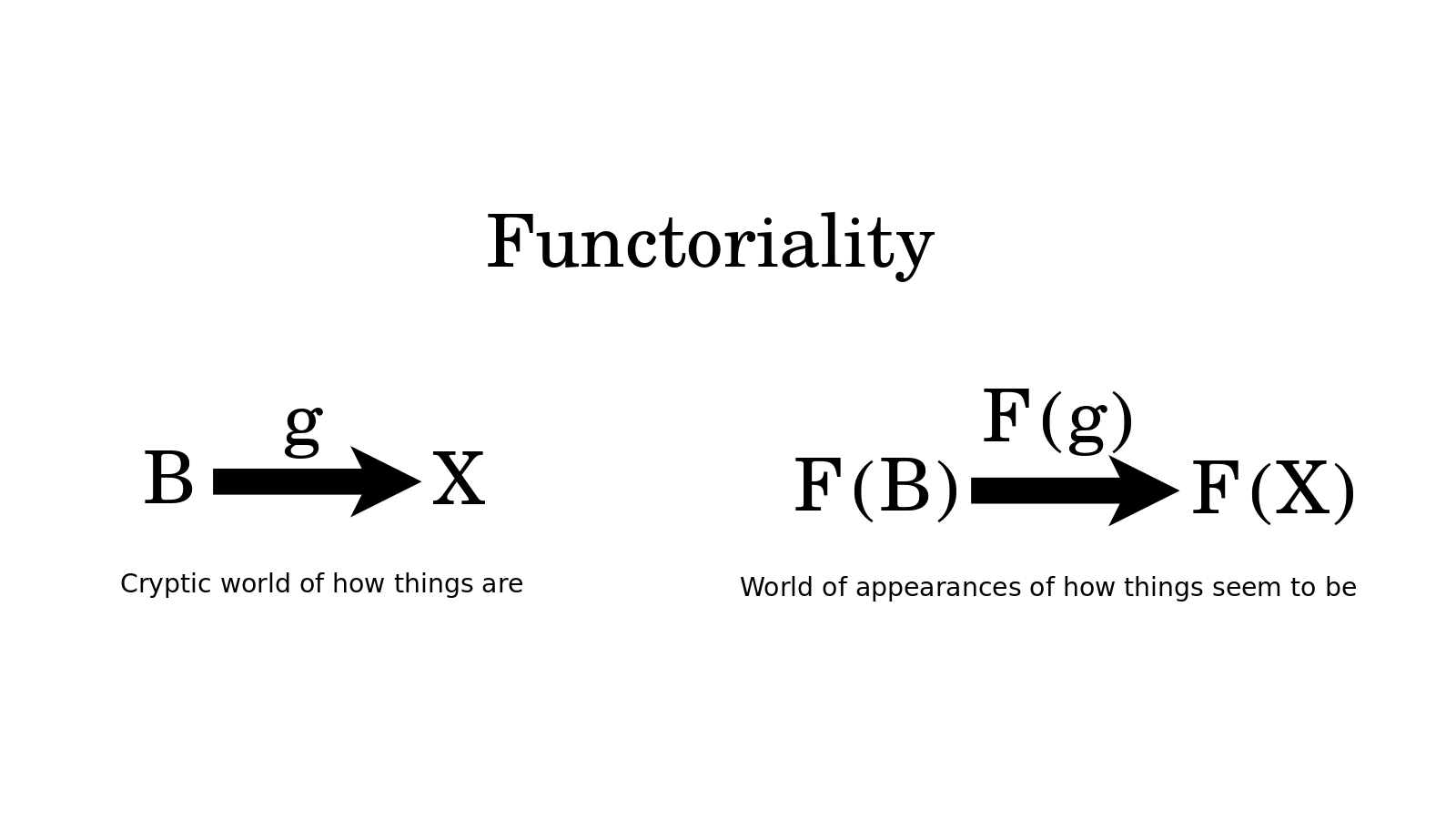
What is more clear in the Yoneda Lemma, however, is that the function {$F(B)$} represents the world of appearances which the functor {$F$} outputs, as when Steve Awodey talks of making a picture. Functoriality is the fact that arrows in the input world lift up to the output world, along with their compositionality, their identity morphisms and associativity.

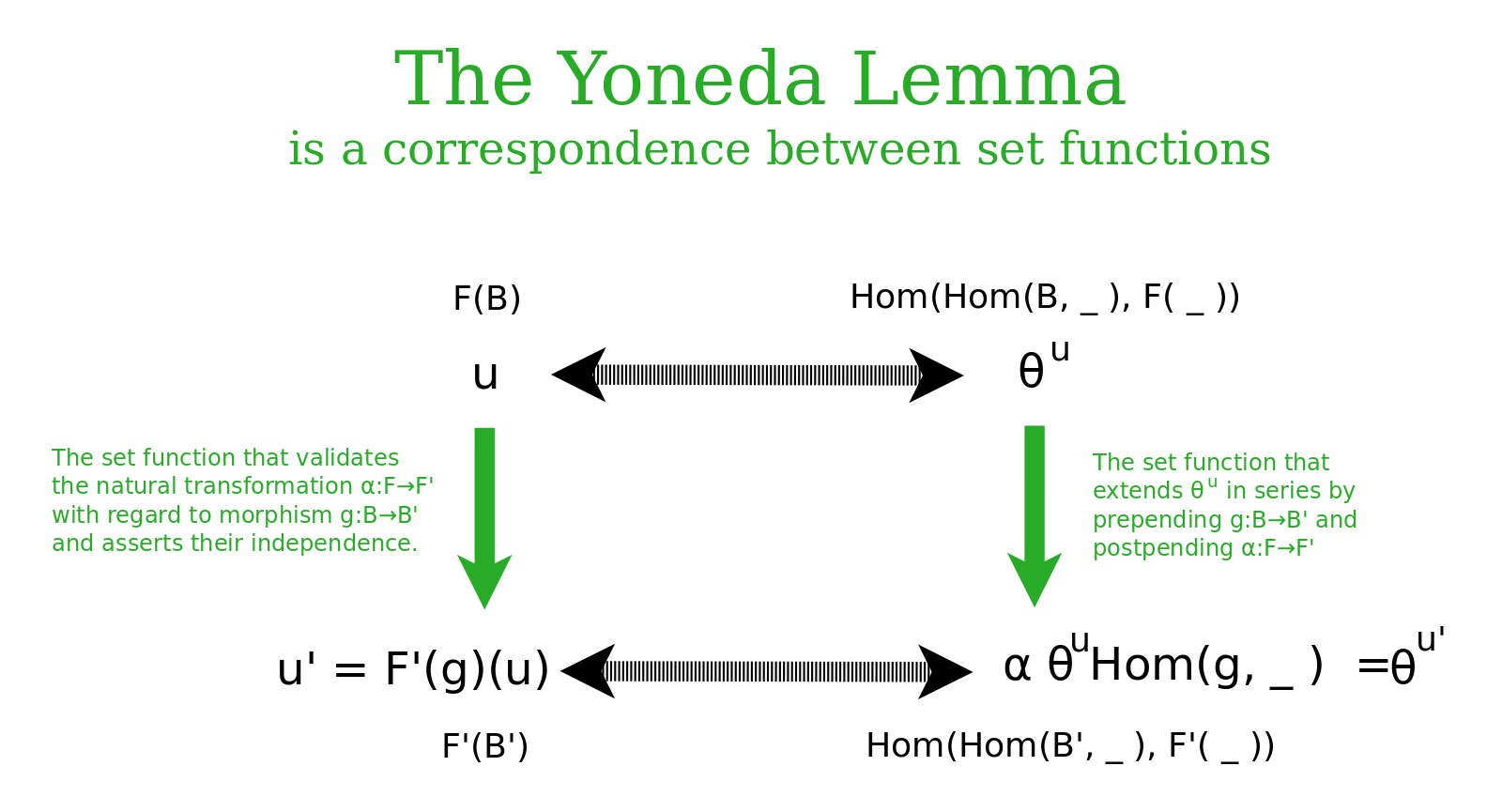
The Yoneda Lemma is a statement about a natural isomorphism which relates two functors, which are two different ways of looking at the same thing. The outputs of these functors is in the world of sets and set functions. So the natural transformations back and forth are expressed as set functions. These set functions are indexed by the objects and morphisms in the underlying world, and are valid for all morphisms {$B'\rightarrow B$} and {$F\rightarrow F'$}.

For the Yoneda embedding, we were describing a bijection relating the arrow in the world of What and the action of laying down an arrow in the world of How. More generally, with the Yoneda Lemma, we have a bijection between elements {$u$} of a set {$F(B)$} in the world of What and the corresponding natural transformation {$\theta^u\in\textrm{Hom}(\textrm{Hom}(B,\_),F(\_))$} in the world of How. This bijection is natural in both {$F$} and {$B$}. Here this means that we can prepend with morphism {$g:B\rightarrow B'$} and postpend with natural transformation {$\alpha:F\rightarrow F'$} and we will get a bijection between elements {$u'\in F'(B')$} and the natural transformations {$\theta^{u'}\in\textrm{Hom}(\textrm{Hom}(B',\_),F'(\_))$}.

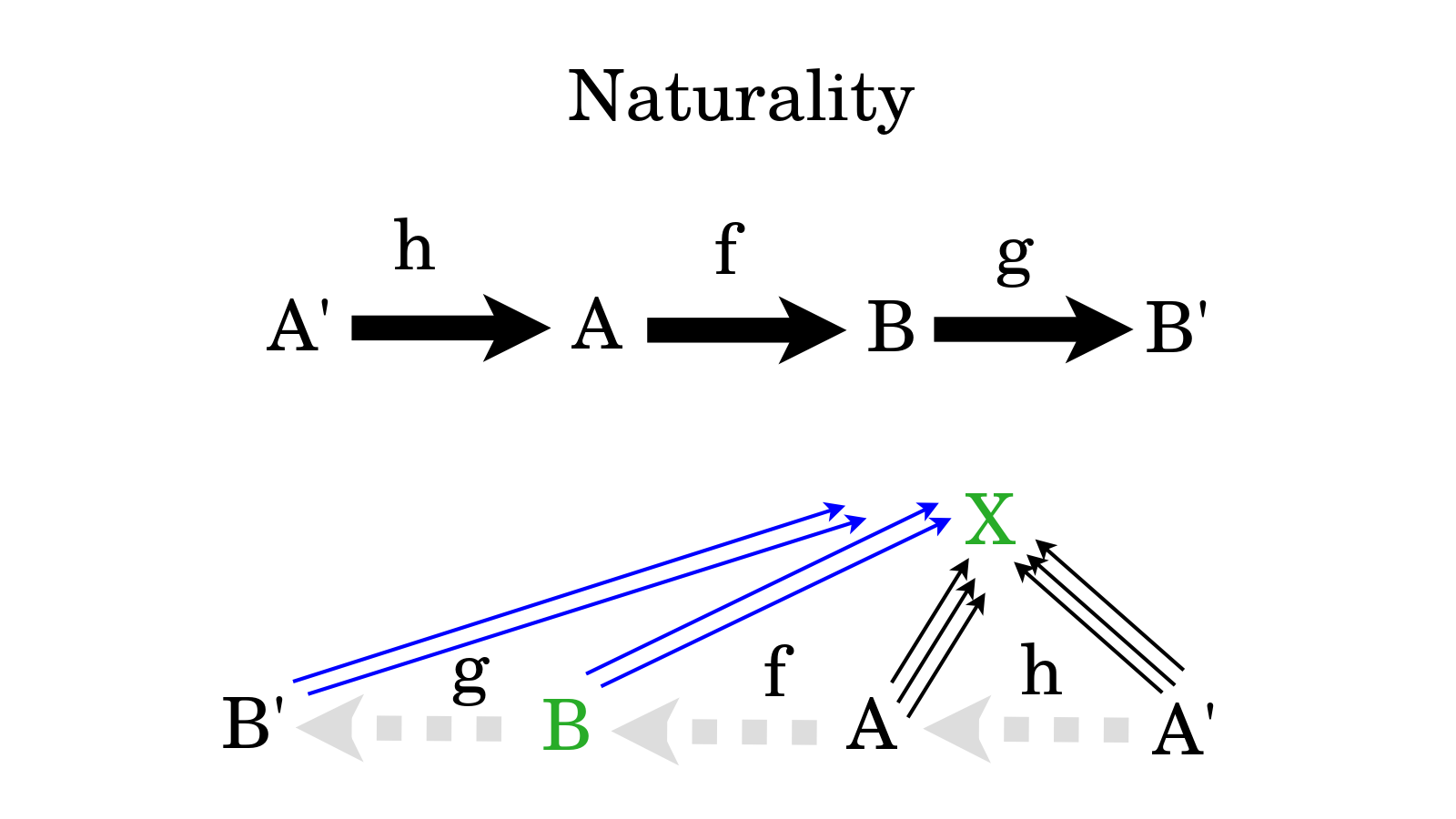
Naturality in the Yoneda embedding means that in our bijection for arrows from {$A$} to {$B$} we can prepend arrows and postpend arrows and it doesn't matter which we do first. We have associativity, and we maintain our bijection for arrows from {$A'$} to {$B'$} relating the worlds of What and How.

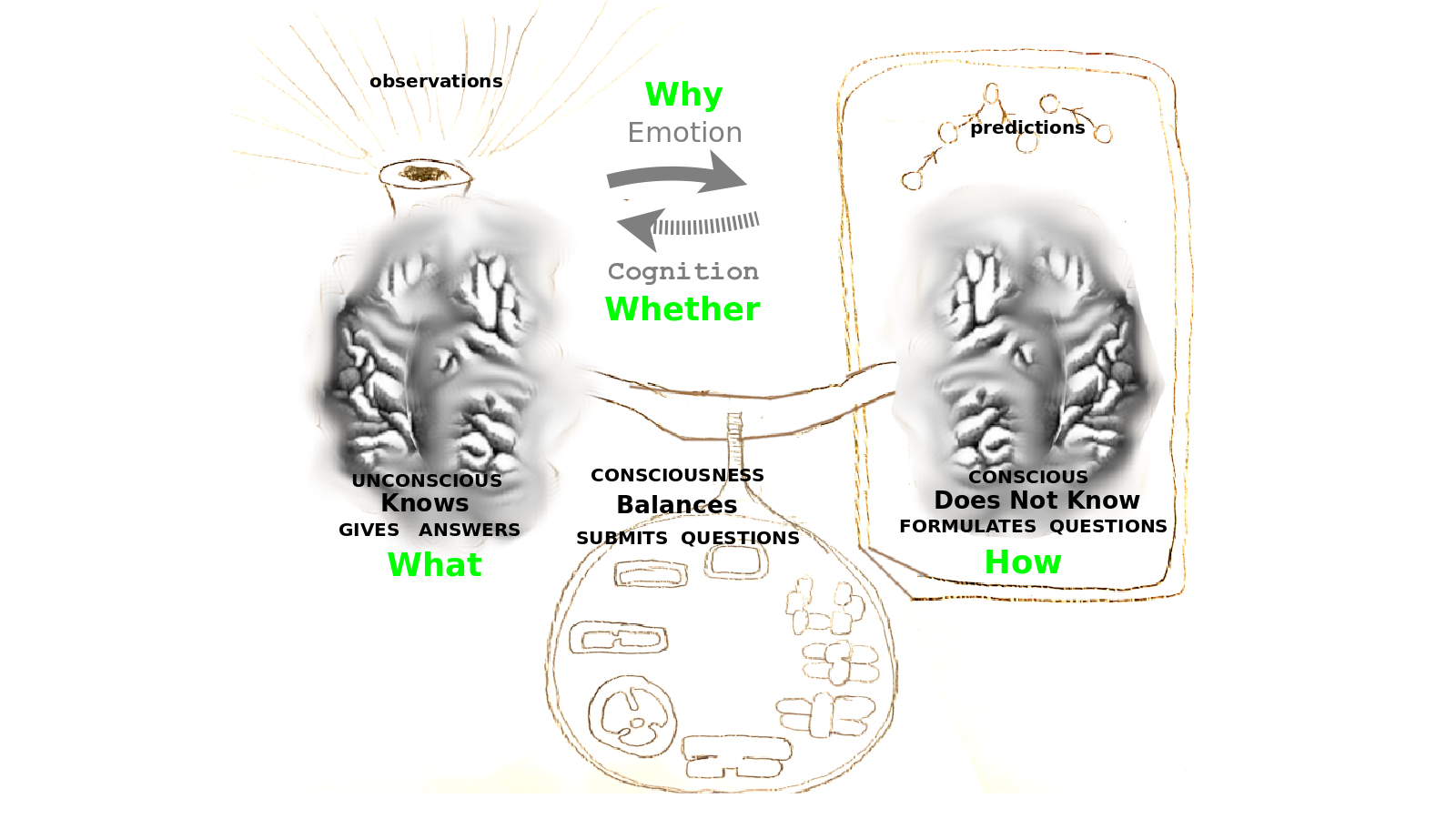
We can think of the Yoneda embedding as modeling the dialogue between two minds, a mind that knows answers and a mind that does not know, thus asks questions which are answered. This dialogue between What and How may be the reason that human and animal brains are divided into right and left hemispheres and likewise they may ground a role for gender in social dialogue. We also can see the two points of view related in Jesus's Great Commandment. In the world of What, we love God directly with all of our body, all of our mind, all of our heart, all of our will. In the world of How, we love our neighbor as ourselves, we love arrow by arrow.

The Yoneda embedding is one example in mathematics that can help us understand the relationship between Whether, What, How, Why. There are many other examples in the insights of profound thinkers and in every day life. We can think of Why as knowledge of everything, How as knowledge of anything, What as knowledge of something, Whether as knowledge of nothing. We have seen the role of the do-nothing action in defining Whether and we could also consider a do-something action that defines What an arrow is, a do-anything action that defines How to prepend an arrow in all manner of situations, and a do-everything action performed by the arrow we extract from its relationships with absolutely everything.

Thank you for considering with me the Yoneda embedding as an example that illustrates the cognitive framework for knowledge in terms of four levels: Whether, What, How, Why. Please let me know if you would like to see more videos on category theory and on this cognitive framework for knowledge. You can do that by leaving comments, liking this video, subscribing to this channel, joining our email discussion group and supporting me through Patreon. I am Andrius Kulikauskas and this is Math 4 Wisdom.