Math 4 Wisdom. "Mathematics for Wisdom" by Andrius Kulikauskas.

A Geometry of Moods

Evoked by Wǔjué Poems of the Táng Dynasty

This is a rerecording, on March 11th, 2023, of an academic talk that I presented on August 14th, 2018, at the discussion panel on Philosophy and Literature at the XXIV World Congress of Philosophy in Beijing, China. I thank the Lithuanian Science Council, which awarded me a travel grant that enabled my participation, and the European Union, which provided the funding, and also my parents Edmundas and Rūta, who provided additional support.

I am Andrius Kulikauskas, host of Math 4 Wisdom. At the end of this video, I add some remarks on how the six geometric transformations I describe are Möbius transformations. This becomes apparent if I rethink the reflection transformation across a line as the more sophisticated and yet more natural inversion transformation across the boundary of a circle. All Möbius transformations can be generated from inversions. The wonderful conclusion is that the mind understands the boundary between the self and the world as a circle on a sphere. And that leads to new ideas for a question that I am currently investigating, What is geometry?

Subjectively, we experience moods in seemingly thousands of different shades. Currently, we have no model for describing their variety. (Ekkekakis, 2013) I sketch a research program of our personal moods to identify, reproduce, contrast, transform, interpret and appreciate them so that we might understand and share them just as we do any language.

Evoking Basic Feelings

A first step is to model our most basic emotional responses. I started with six responses which are essentially those which psychologists Paul Ekman and Harriet Oster found can be observed in the faces of young infants, namely: happiness, sadness, excitement, surprise, fright and disgust. (Oster & Ekman, 1978) What is the simplest way that I might evoke these responses within myself? I once read that we are struck by existential sadness when our deeply held assumptions turn out to be wrong. So I imagined myself as a child playing with alphabet blocks. I would pick up a block, guess what letter was on the other side, and see if I was right.

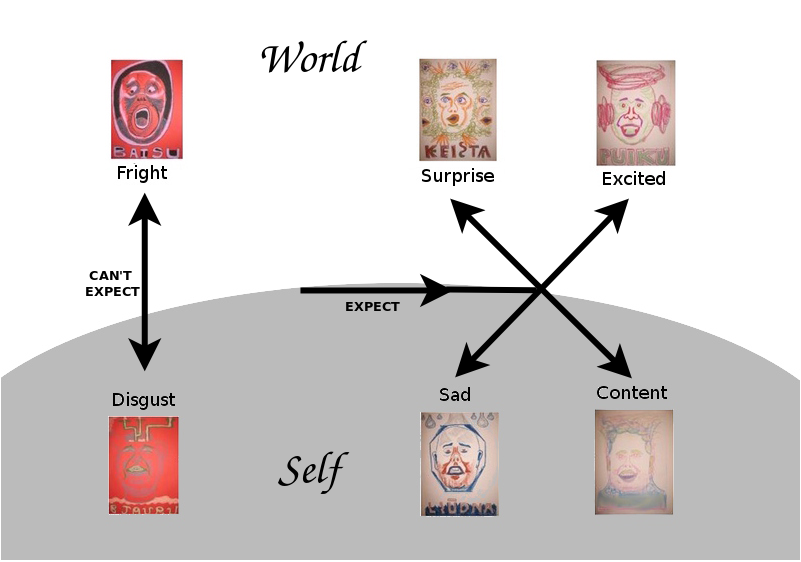
Suppose I don't know the block very well. If I guess wrong, then I am surprised, but if I guess right, then I am excited. However, if I know the block with absolute certainty, if I can't imagine I could be wrong, if my self and my world depend on that, and yet indeed I am wrong, then I feel devastated, but if I am right, I feel content and assured. And so by such introspection it is clear that our cognition grounds our emotion. A crucial distinction is between that knowledge which we personally identify with, by which we define ourselves, and that knowledge which is more distant, exploratory, theoretical. Furthermore, when I experience what I can't in any way expect because it is too sudden, too strange or too undesireable, then if it comes from beyond, I am frightened, and if it comes from within, I feel disgusted.

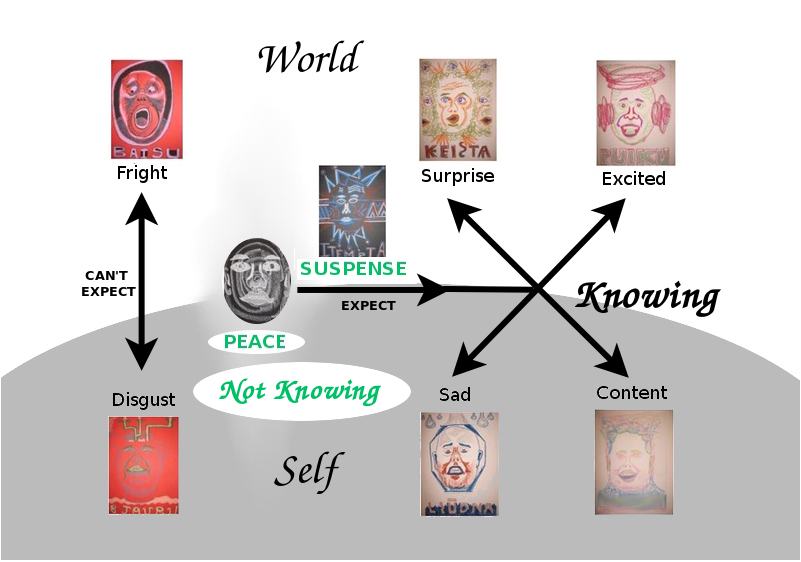
The structure of this model gives subjective meaning to the facial expressions we observe. It also makes sense of two emotional responses which we can introspect but which we do not and cannot observe, namely peace and suspense. We feel suspense after we have made an expectation and before we know whether it has been met, and we feel peace when we make no expectations. These are responses of not knowing, whereas the other six are for knowing. We see from this model that seeking peace (which has us be sensitive to all emotions) and seeking happiness (by avoiding sadness) are two very different approaches to living.

We can thus evoke distinct, basic, pure, vivid emotional responses by manipulating abstract expectations. It is remarkable that psychologists have not appreciated the significance of our imagination's ability to evoke feelings. They focus on physiology and conclude that there are no basic emotions, indeed, no reproducible emotions, because they lack any consistent expression. (Barrett, 2017) It is as if they were linguists for whom shouting and whispering were different activities and who never understood that they may convey the same name. They do not appreciate the mind as an abstract system of activity which maintains a coherence that need not have any particular neurological analogue.

Proceeding similarly, we can show how to evoke other feelings including fright and disgust; suspense and peace; anxiety, anger and hate, relief and depression; beauty, intimacy and love; humility and resignation, guilt and shame, self-assurance and pride; empathy and humor; pleasure and pain.

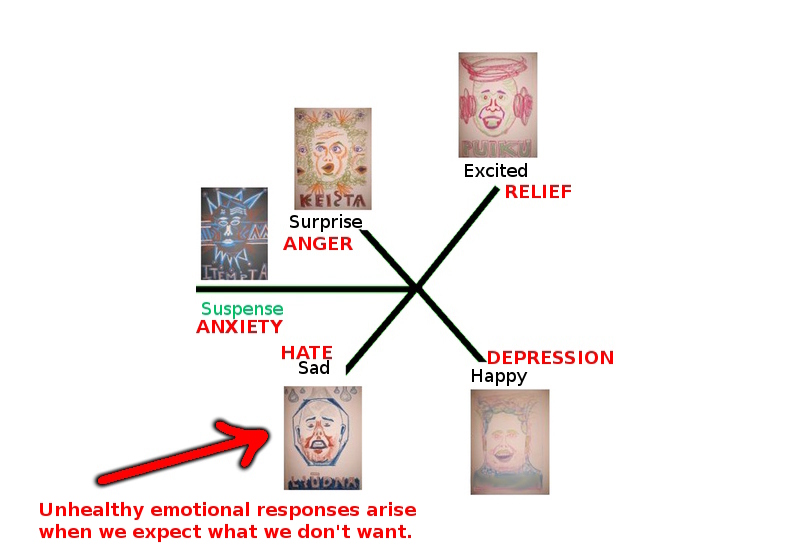
Negative moral tones arise when we expect that which we do not wish. For example, if I expected to find my bicycle where I left it, then I will be surprised if I don't; but if I expected it to be stolen, then I will be angry if it is, but relieved if it is not.

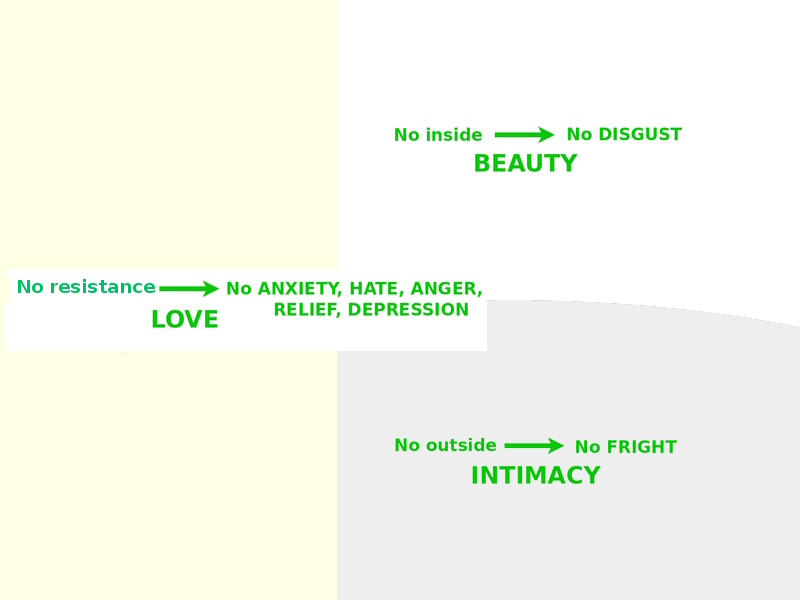
We feel positive moral tones as the impossibility of negative moral tones. For example, if we perceive that everything is outside of us, then disgust is impossible, and so we feel beauty. Thus we feel beauty not as our own emotional response, but rather as an afterglow, emanating from our beautiful environment.

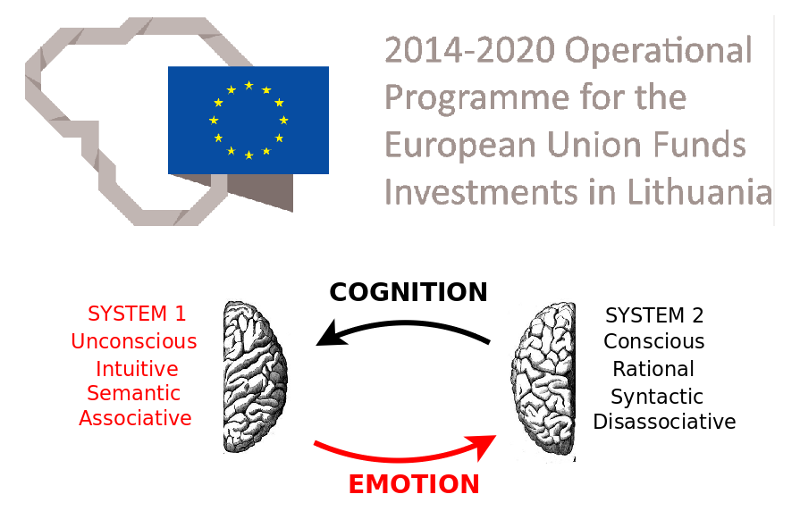
This model also draws attention to the role of the conscious and unconscious. I may consciously expect that my wife will die from cancer, but my unconscious mind may yet expect otherwise, holding true to my desire that she live. This may evidently be healthy. Thus this model suggests itself as a tool for investigating such distinctions between our conscious and unconscious, or in contemporary terms, Kahneman's System 2 and System 1. (Kahneman, 2011)

Studying How Poems Evoke Moods

Psychologists only distinguish between good moods and bad moods. But let us now investigate how our expectations can give rise to a language of thousands of moods. We might study music, dreams, activities, but especially, poetry. Are two people able to interpret a poem in the same way so that it evokes the same mood?

Quiet Night Thoughts, by Chinese poet Li Bai of the Tang Dynasty, is a classic poem about his travels far from home.

 Bed. Beyond, bright moon shines.
 Seems like on the ground is frost.
 I raise my head - see bright moon.
 I lower my head - think of home.

Note how this poem organizes the spaces for our expectations. The bed is a boundary beyond which we feel the moon is beautiful and the frost is surprising. The poet's neck, which raises and lowers his head, is yet another boundary. The poet thinks of home, which is dear to him, and of itself that surely makes him happy. Yet when he contemplates that his home is so distant, it is sad to think that he is here and not there. Overall, we can specify a mood of conditional sadness, which depends on his reflection on his great distance from his happiness, as measured by the beauty of the moon and the surprise of the frost.

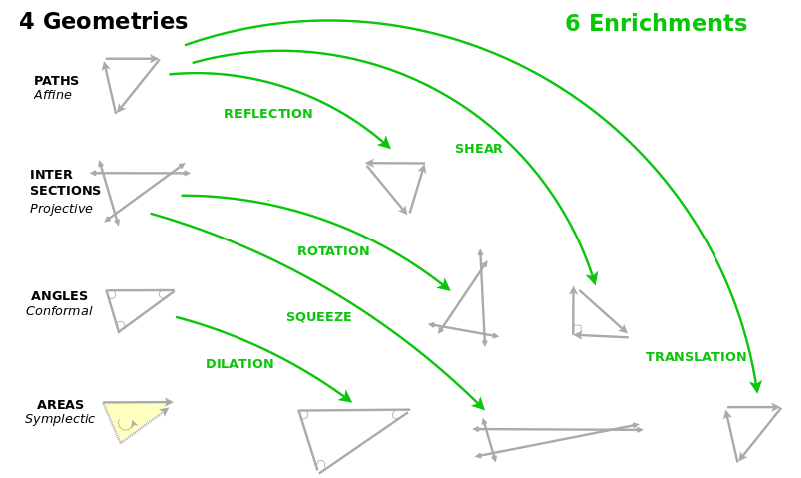
I made a study of 37 classic wŭjué poems (five-character quatrains) from the reknowned collection "Three Hundred Tang Poems" (Tángshī sānbǎi shǒu). (Bynner Jiang, 1972) Each poem made use of one of six different transformations of the boundary that defines the self and world which are familiar to geometers: reflection, shear, rotation, dilation, squeeze and translation. These transformations are six ways of enriching a geometry.

In the simplest affine geometry, a triangle consists of three paths from A to B to C. In a projective geometry, it consists of lines intersecting at A and B and C. Lines moving back and forth allow us to confront our own moods. In a conformal geometry, it is formed by angles at A and B and C. This lets us admit of other moods, perpendicular with ours or not. And in a symplectic geometry, it is an oriented area defined by A and B and C. Here we may attribute a mood to our environment.

A reflection allows us to look back upon ourselves. A shear transformation lets our view be perpendicular to that of another who sees what we don't see. A rotation lets our view dance from point to point. A dilation has our view expand it, whereas a squeeze transformation has it keep the same area but recast the proportions of its shape. A translation has us move to a new situation. I simply wish to suggest that conceptual geometry is the key to an interpretation of the situations which define the boundary between our selves and our world which determines our mood.

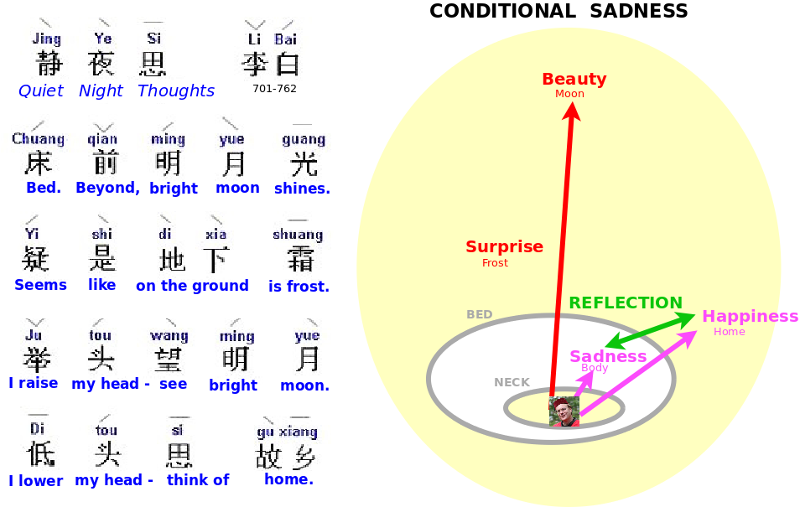
7 poems establish a mood by reflection. I see myself, as if in a mirror, in a foreign world: I talk up a boatsman, whether he's from my village; in my dashing enemy I perceive my own ambitions. In Li Bai's poem, Quiet Night Thoughts, his bed marks the boundary between familiar and foreign.

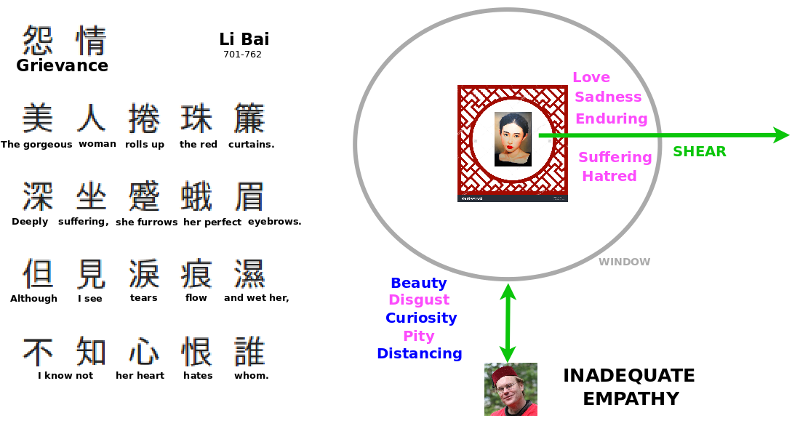
4 poems establish a mood by a shear transformation, that is, by defining perpendicularity: flowers bloom apart from us; I awoke to realize I had slept through a passing storm; one must comport oneself anew after inauspicious omens; venerable ladies discuss the absent Emperor. In Li Bai's poem, Grievance, an injured beauty opens her window, but I remain disengaged.

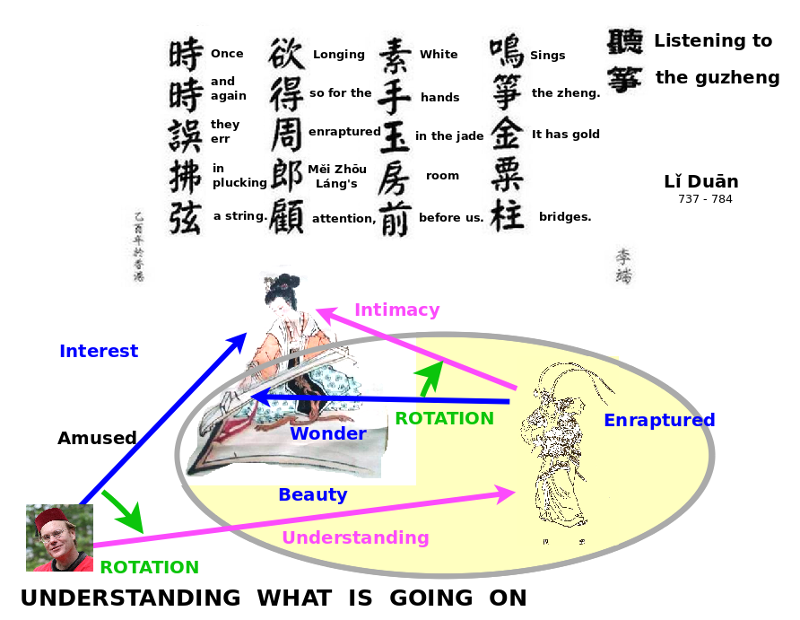
5 poems establish a mood by rotation, turning our attention. A sensitive friend, however far away, will hear the falling of the pine cone, which I hear in the stillness of the mountains. The buddy at my side may succumb to temptation to drink a cup of wine. A general will shoot an arrow blindly into the storm and, in the morning, find it driven into a stone. In Li Duan's poem, Listening to the Guzheng, the harpist commands not only of the warrior's attention, but mine own, as well.

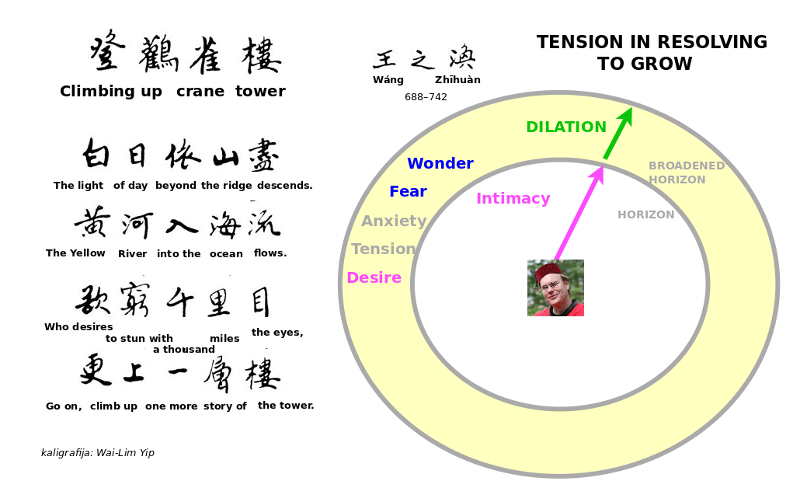
7 poems establish a mood by dilation, that is, by increasing or decreasing scope. That is our relationship with our environment and its mood. Mountains and paths are snowed over, as if there were no boundaries, and yet we see a fisherman, all alone, in his small boat, covered by his bamboo coat, his personal boundary. Stopping at the edge of the wilderness, as the plains open up, a traveler is overcome by sadness, he feels himself too large, but then the moon draws near, reflected in the creek. (This is an example of how one transformation may be extended by another, even in a short poem.) Wang Zhihuan's poem, Climbing Up Crane Tower, widens endlessness, as you imagine climbing one more flight of stairs.

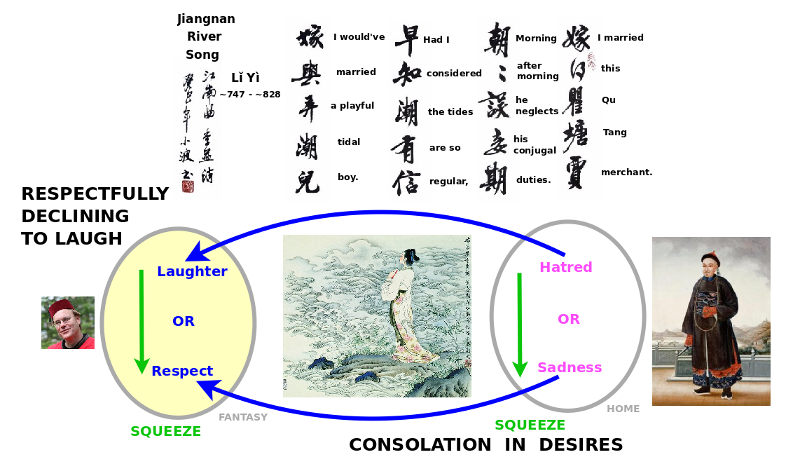
9 poems establish a mood by a squeeze transformation, whereby an area remains constant but its proportions change. Similarly, a poem may relate a general's silk flag with a thousand shouts from the tents. Li Yi's poem, Jiangnan River Song, considers is a wife better off with an inattentive merchant or a commoner who is regular as the tides.

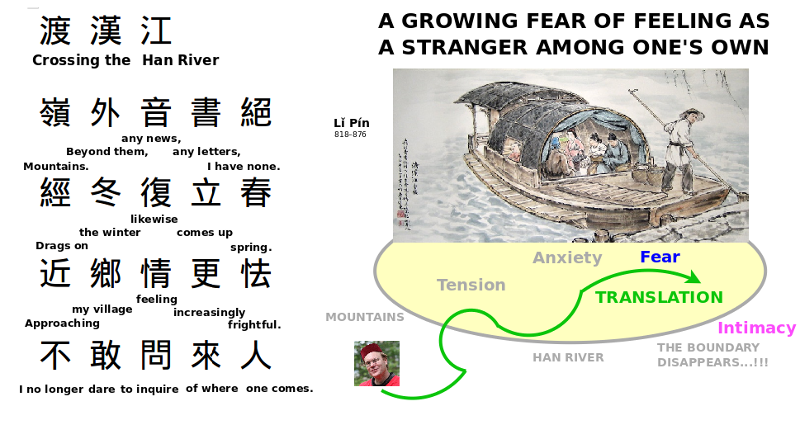
6 poems establish a mood by translation. The elder dame of the estate comes to tears from hearing a song of her homeland. Li Pin feels a growing fear, as he gets closer to home, that he will feel a stranger there, in his poem, Crossing the Han River.

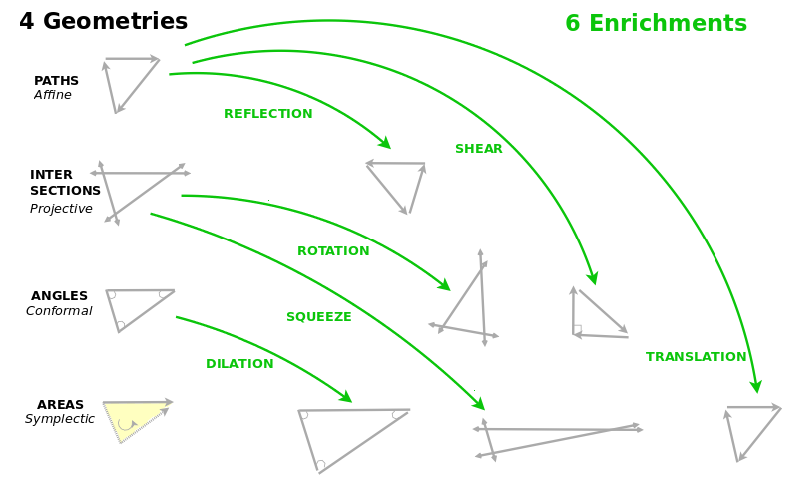
All 37 poems nicely distributed themselves according to these six geometrical transformations. This suggests that spatial relations are the key to the mood which a poem establishes. And the purpose of that mood and of the poem, I believe, is to foster our growth to empathize with others, to know ourselves, and to develop commonality. Classic poems let us believe that they can indeed evoke in us specific, comparable, well defined moods. Working further, we may truly externalize this internal language of moods.

Thank you to Sylvain Poirier for his online notes about geometry from which I made use of the six transformations he described.

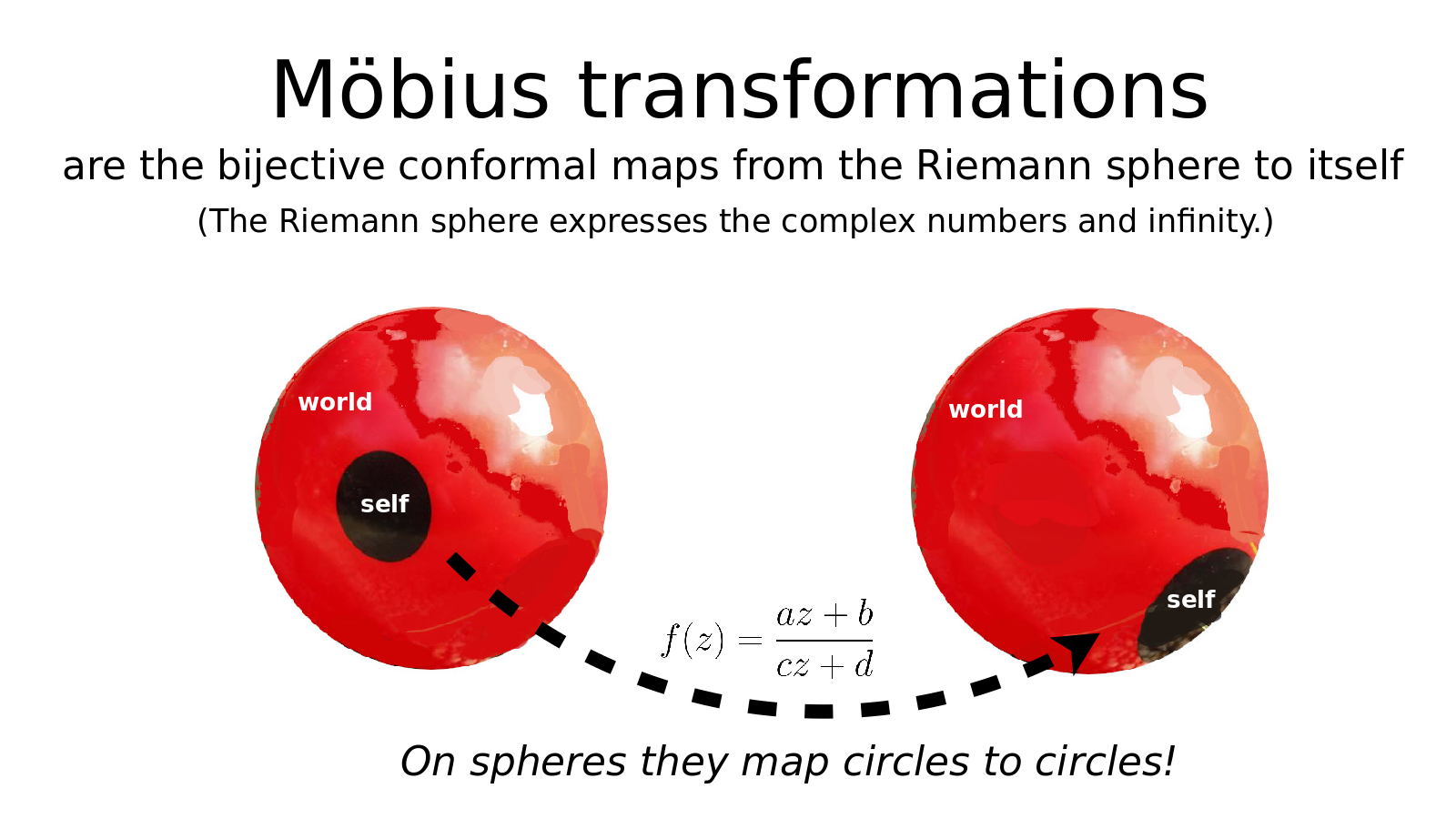
Several years after this presentation I wondered where these six transformations appear in mathematics. I learned about the Möbius transformations, which are functions of the form f(z) = (az+b)/(cz+d) where z is a complex number and so are a, b, c and d. We can add a point at infinity to the complex plane, yielding the Riemann sphere, and then Möbius transformations map the Riemann sphere onto the Riemann sphere, bijectively. These maps are conformal, which means they preserve angles. They map circles to circles. This suggests that we think of the boundary between the self and the world as the boundary that separates a circle from what is beyond.

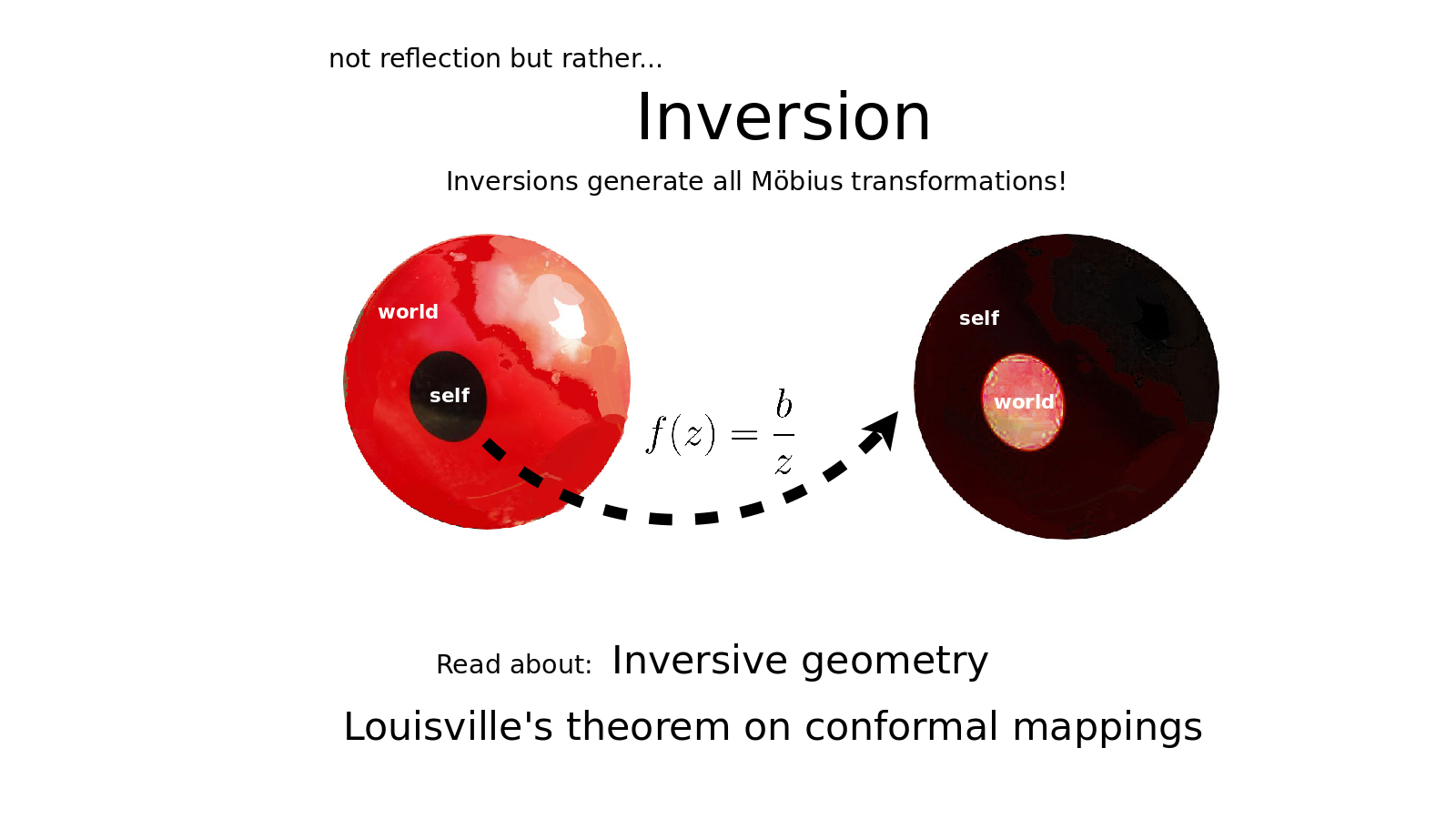
The Möbius transformations include all six transformations but I was missing the most important one, which is inversion. The function f(z)=b/z swaps the inside of a circle with the region beyond it. This expresses well what I had called reflection in the poem which starts "Bed. Beyond, bright moon shines." This is not reflection across equal territories but rather inversion out of the circle which surrounds the poet, namely, their bed. Inversions back and forth generate all of the Möbius transformations. Whereas reflection is understood mathematically as dilation with a negative sign.

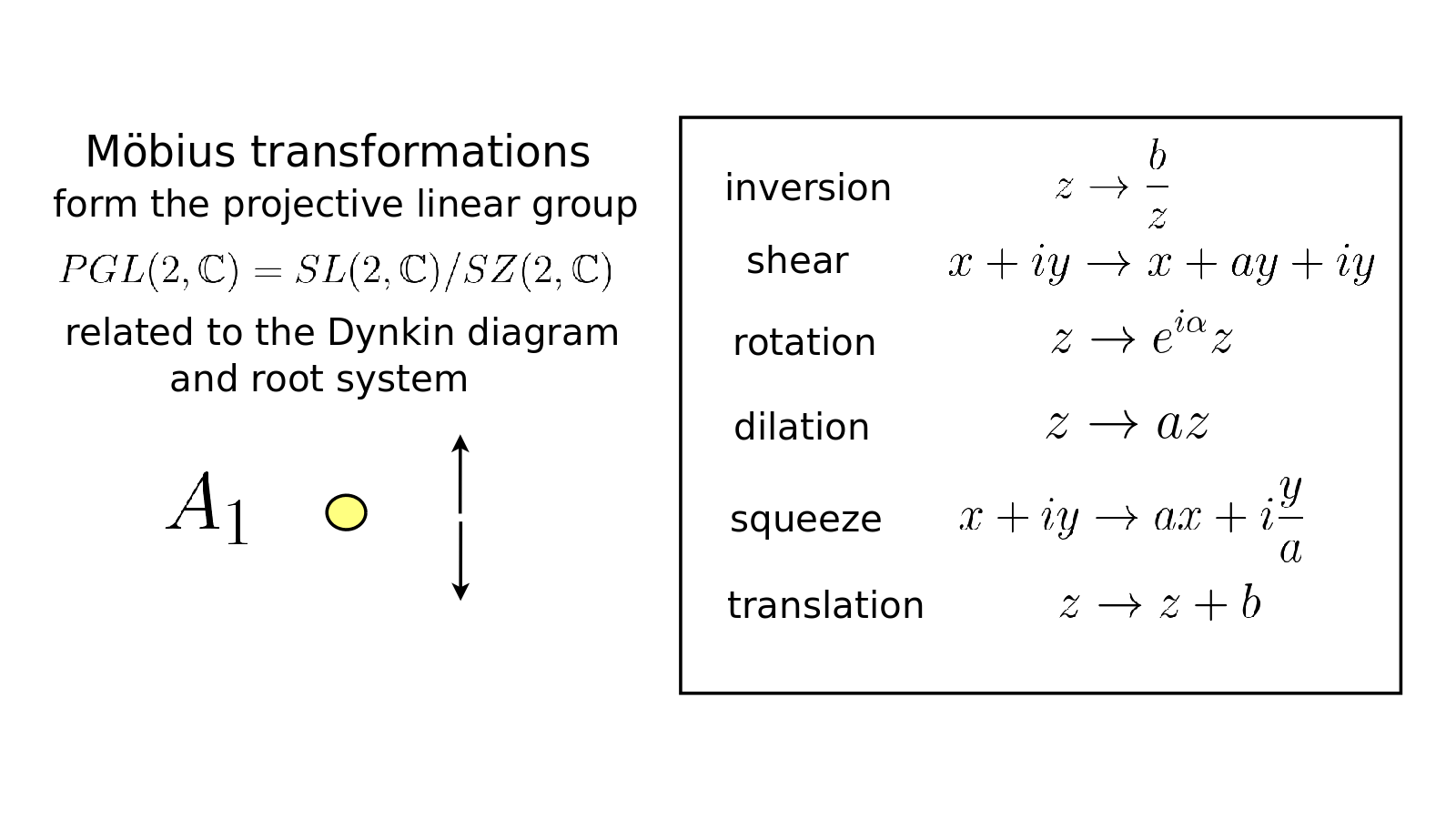
Möbius transformations form the Möbius group, also known as the projective linear group. This is related to the special linear group SL(2), which has the most basic root system, {$A_1$}. Mathematically, we can study the nature of these transformations and their relationships. A lot is known about that.

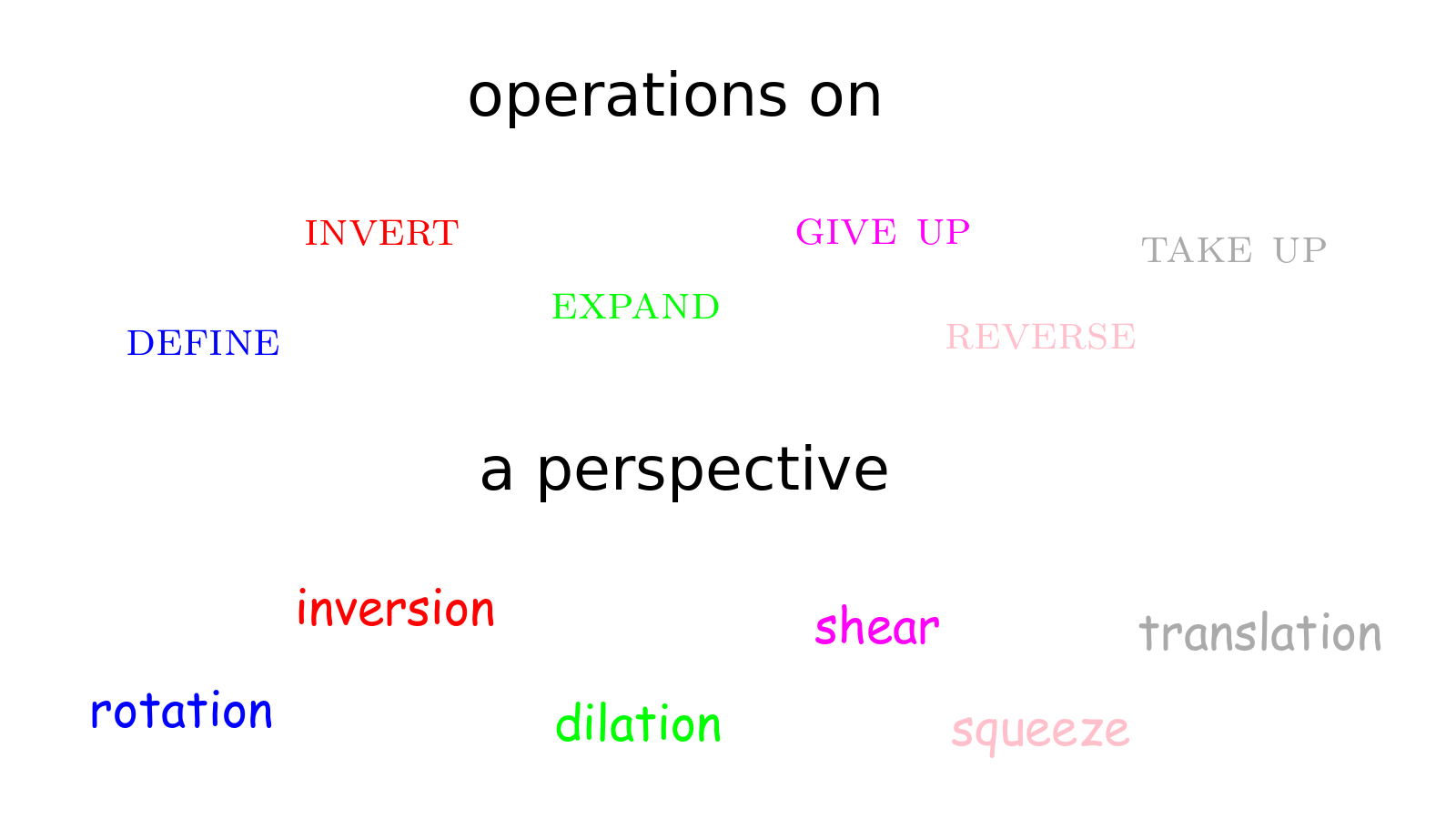
Philosophically, we can think of a circle on a sphere as modeling a perspective. The transformations may correspond to the ways the we relate to a perspective, the operations on perspectives. We can define our perspective and then expand it. We can give up our perspective and take it up again. We can invert our perspective, looking back at ourselves, but we can also reverse our perspective, switching its direction. Such a reversal happens when we reflect upon ourselves.

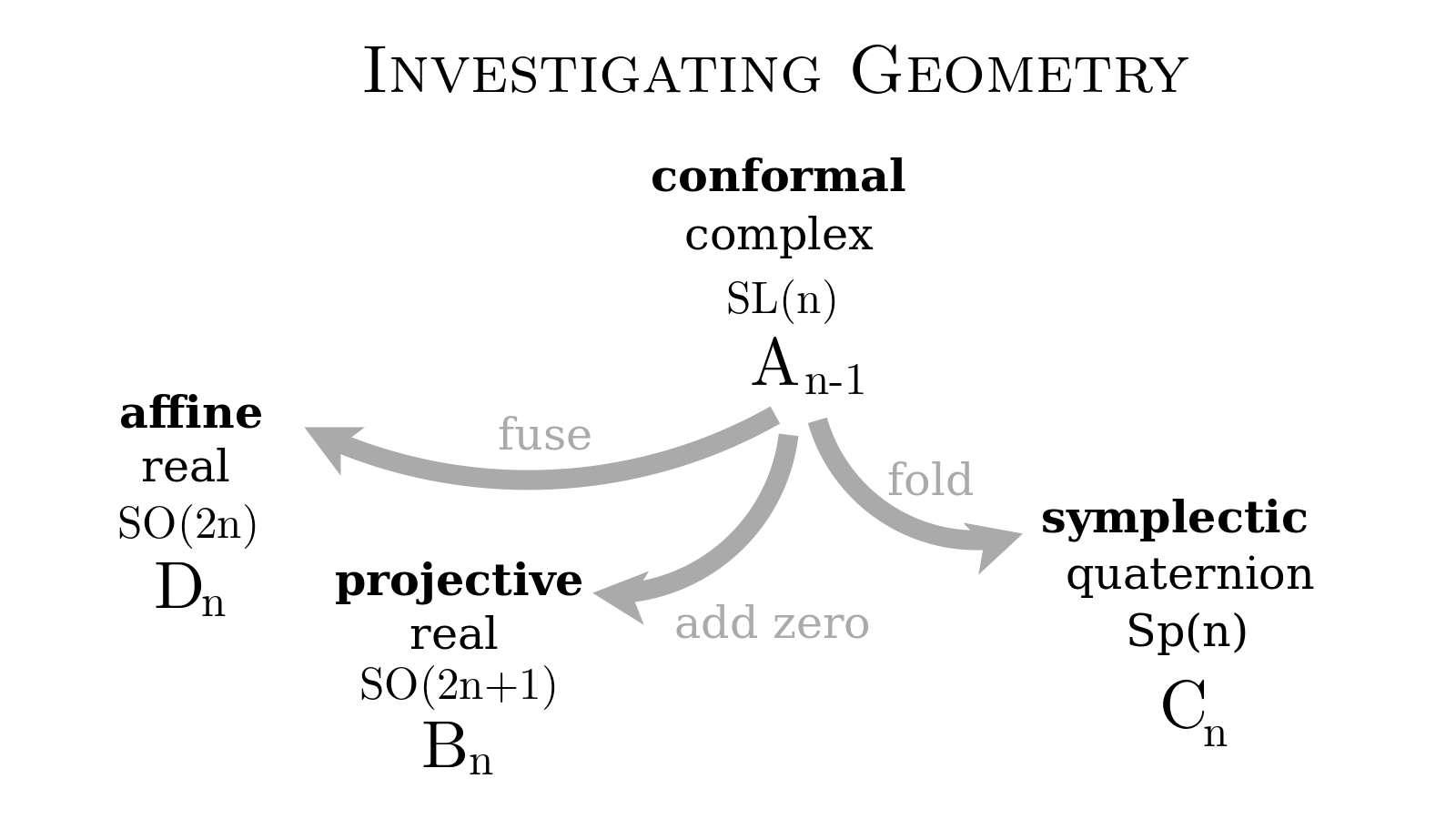
What Möbius transformations describe is apparently the most basic geometry, the one which makes sense for a baby in the womb, or a newborn baby or any such being which spends time by itself, with a scarcity of external stimulus, and thus may contemplate, for example, its relationship with the unknown, I may say, with God beyond. Inversions model how I imagine God going beyond herself into herself, thus creating her self. And they model how we go beyond ourselves out onto the God beyond.

This geometry is grounded in the most basic numbers, which are called the complex numbers, and which relate two dimensions so that there can be rotations, as with circles. This is the conformal geometry that preserves angles. We know from Lie theory that there are three other classical families. I am investigating how they may ground three additional geometries. In a future video, I will explain how the root systems variously encode the duality in the counting of numbers forwards and backwards. For now I will simply say that the two-dimensions can be split, which I suspect yield affine geometry or projective geometry, based on vector spaces in even or odd dimensions over the real numbers. Or the two-dimensions can be folded, so to speak, doubled, pairing position and momentum, yielding four-dimensional vector spaces based on quaternions, grounding symplectic geometry.

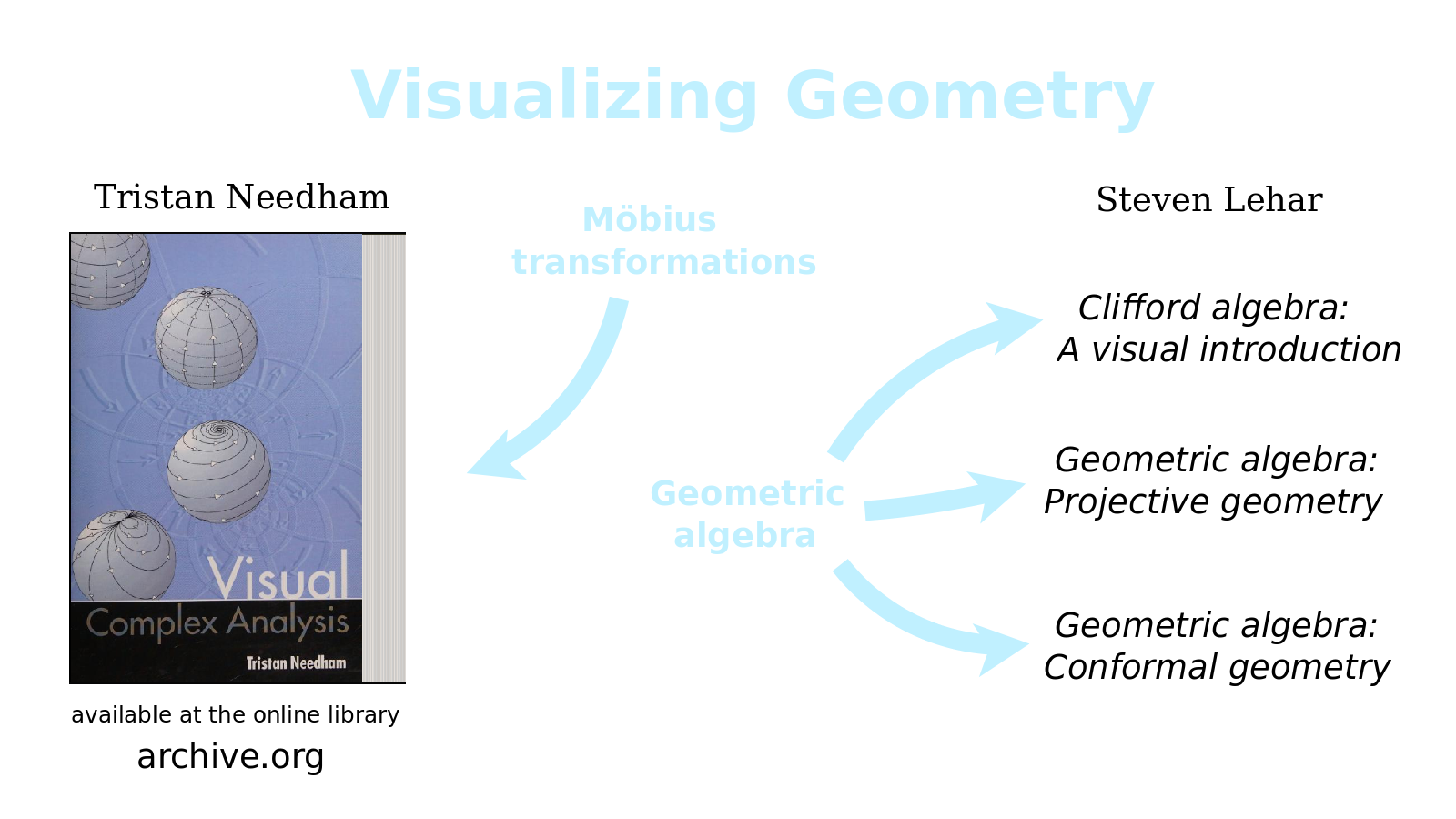
At this point, I look forward to studying with you and others to learn more about Möbius transformations and how they relate to various geometries. A classic book to study is Visualizing Complex Analysis by Tristan Needham and it is available online. I am also intrigued to think about the articles by independent researcher Steven Lehar, with a PhD in Cognitive & Neural Systems, who argues that the world we see around us is actually inside our head. Furthermore, the form that it has inside our head is shaped very much in the spirit of the geometry of Moebius transformations. His works offer a thoughtful opportunity to delve into Clifford algebras, geometric algebra, projective geometry, conformal geometry and perhaps symplectic geometry. These topic can further take us to Bott periodicity, which is a key phenomenon in advanced mathematics that may model the eight-cycle of mental states, what I call divisions of everything, divisions of our mind's mental sphere, the brain's global workspace.