• View
• Edit
• History
• Print

---

Jere describes the TimberFish Table Top Unit

Marcus will present Econet Action Plan at IAS Commons

Andrius models Active Inference with triangle centers

---

Welcome to Math 4 Wisdom. Read the transcript and watch the video.

Andrius Kulikauskas hosts Math 4 Wisdom	Learning Paths in Math 4 Wisdom

Math 4 Wisdom is an investigatory community for absolute truth led by Andrius Kulikauskas. That's me!

---

• Research.Notes . . . April 17, 2025, at 05:36 PM by AndriusKulikauskas:
• Research.Hamiltonians . . . April 16, 2025, at 03:18 PM by AndriusKulikauskas:
• Research.BottPeriodicityForOctonionManiacs . . . April 14, 2025, at 07:53 PM by AndriusKulikauskas:

---

We present our ongoing research at the Math 4 Wisdom YouTube channel.

Please join us! Our social hub is the Math 4 Wisdom Email Group. You can subscribe or unsubscribe yourself. Here is our archive. Thank you, Marcus Petz, Leland Beaumont, Jere Northrop, Jon Brett, Ryan Buchanan and all for your thoughtful letters. My letters include:

Andrius Kulikauskas and our study group leaders

Our activity focuses on our study groups.

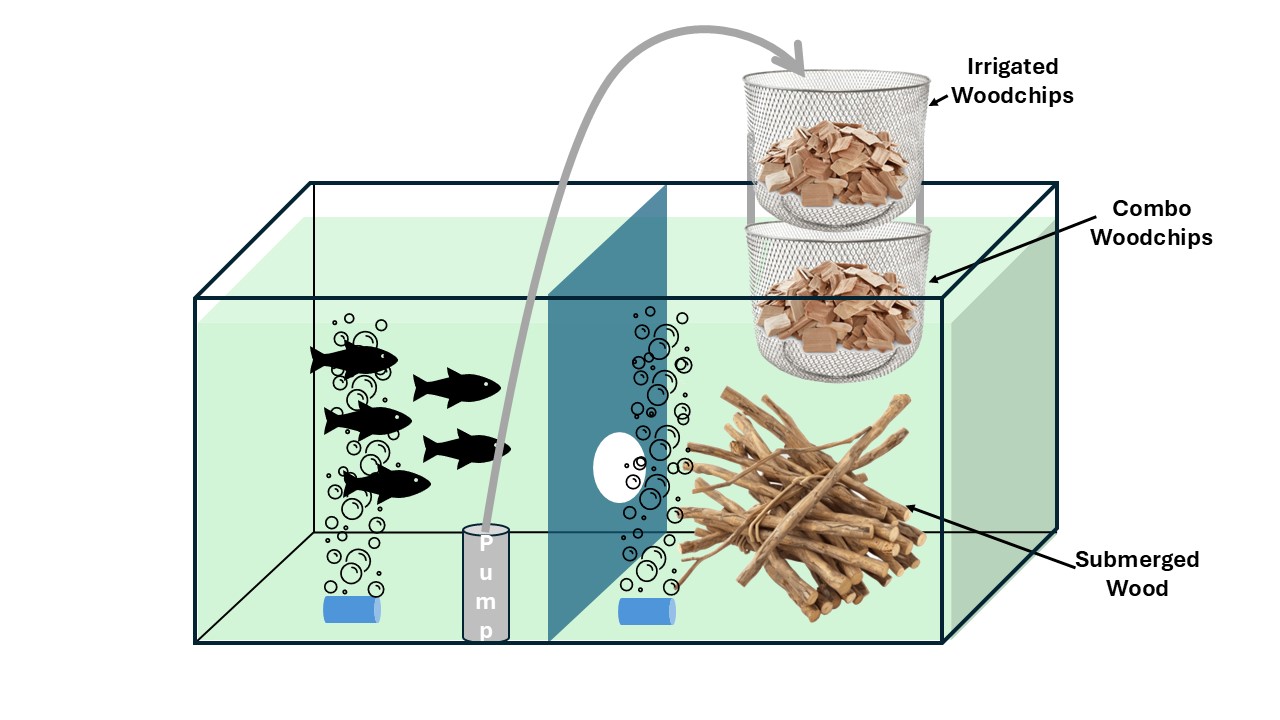
• Jere Northrop : Language of Wisdom Jere is a cofounder of Timberfish Technologies. He has a PhD in biophysics, is an innovator in environmental technologies, and has thought through a constructed language, Ododu, inspired by the Relational Symmetry Paradigm.
  • Jere and Andrius are discovering fundamental connections between their languages of wisdom, Relational Symmetry Paradigm and Wondrous Wisdom, respectively.
  • Andrius is documenting Jere's knowledge of the ways of figuring things out in ecotechnology.
  • Jere is developing ecotechnology with Ecological Intelligence for a new version of Timberfish Technologies.
  • Andrius is trying to describe three conceptual languages by which we experience life: argumentation by which issues come to matter, verbalization by which concepts acquire meaning, and narration by which events happen.
• John Harland : Physics John has a PhD in functional analysis. He teaches math at Palomar College.
  • John seeks to contribute to a more solid or plausible ontological foundation for physics.
  • John is exploring, Does an apparent time factor of {$\frac{1}{2}$} arise in comparing classical and quantum unitary representations of relativistic dynamical systems?
  • John is currently studying the Dirac equation, spin {$\frac{1}{2}$} and {$SU(2)$}.
  • Andrius is exploring double causality as a framework for physics. He is investigating the combinatorics of orthogonal Sheffer polynomials to develop a combinatorial interpretation of the Schroedinger equation which may work for quantum field theory as well.
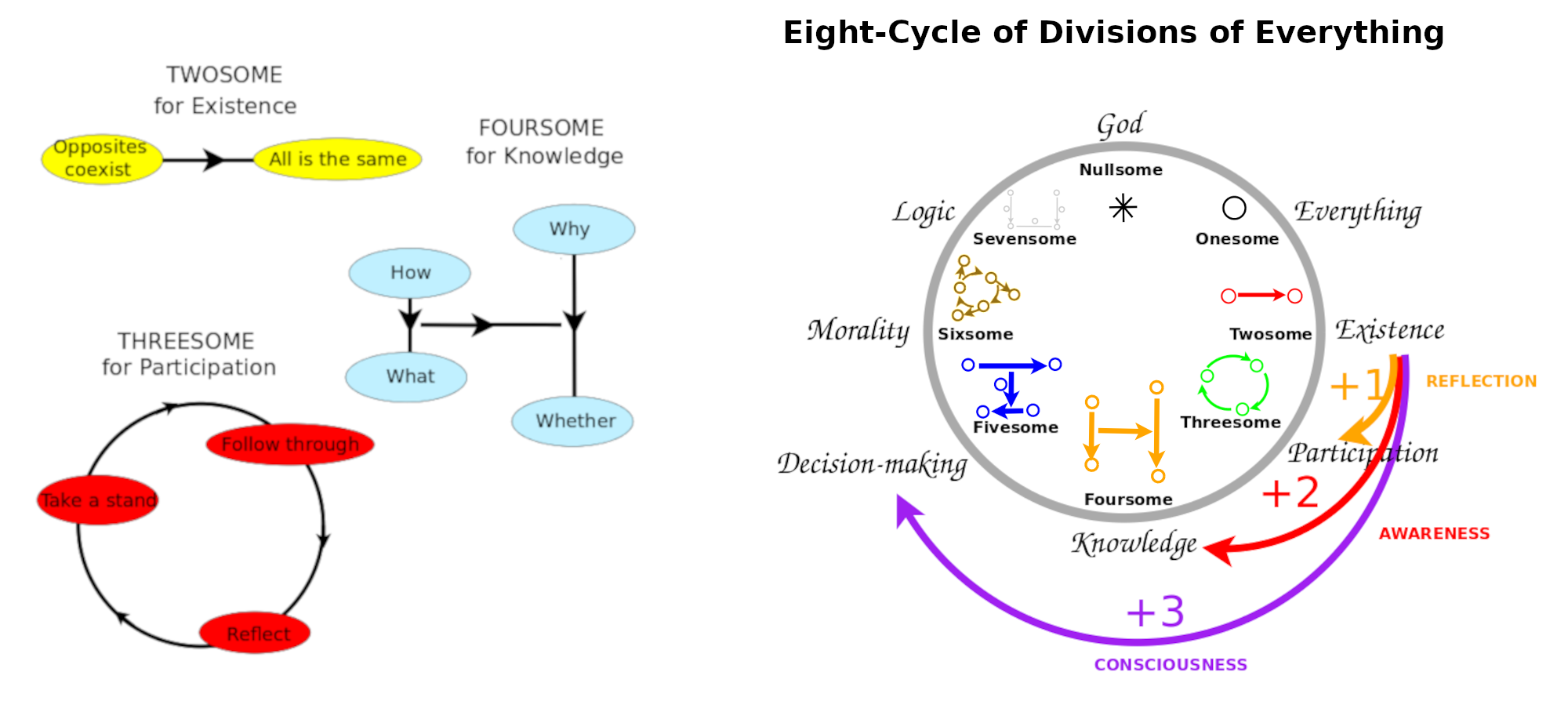
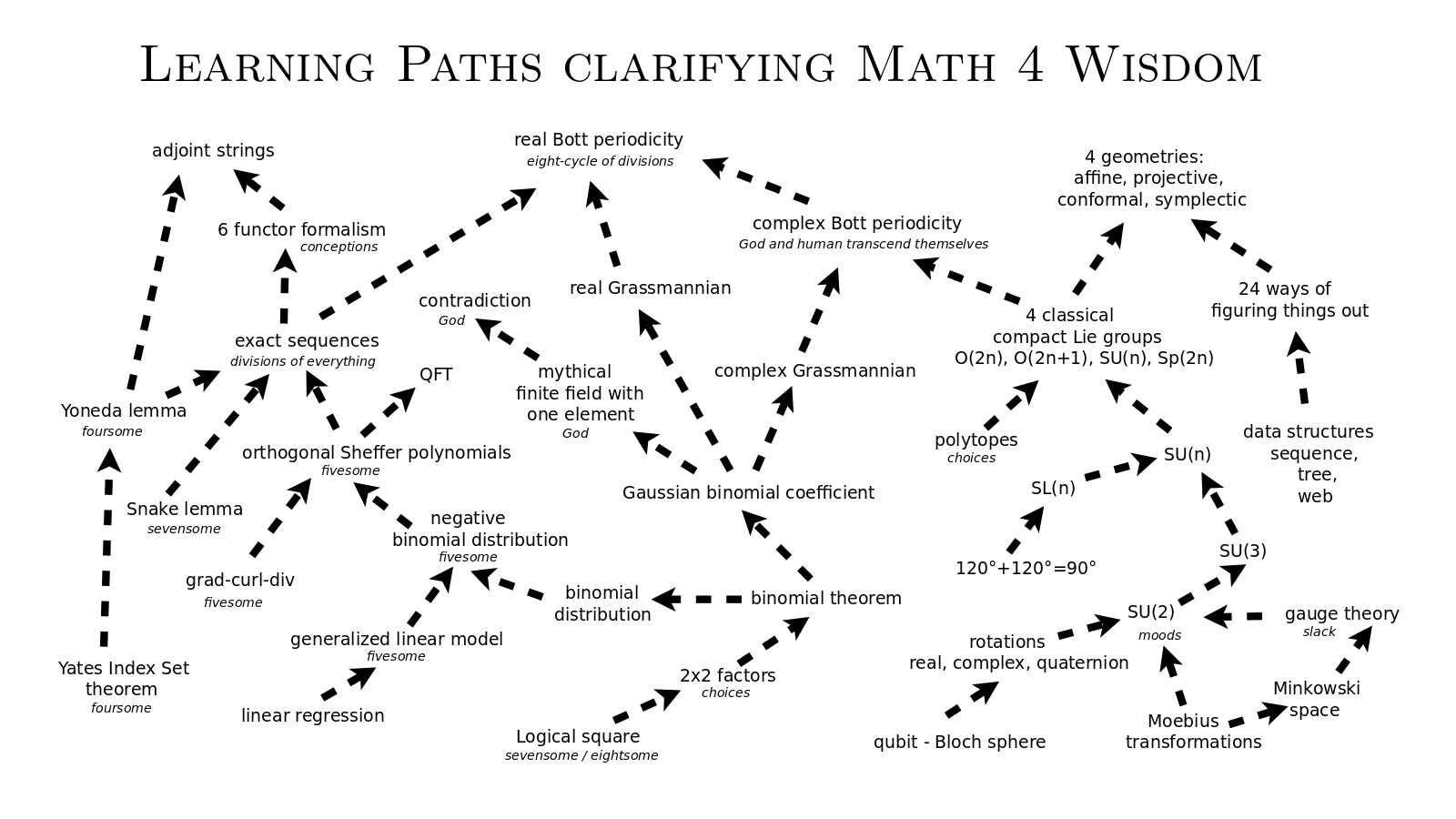
  • Andrius is exploring advanced mathematics for expressions of fundamental cognitive frameworks - the divisions of everything. In particular, he is studying Bott periodicity, Clifford algebras, chain complexes, category theory, orthogonal Sheffer polynomials and the foundations of geometry. This overlaps with John's interests, including in Lie theory and spinors.
• Daniel Ari Friedman : Knowledge Engineering / Knowledge Math Daniel is President of the Active Inference Institute. He received his PhD in Ecology and Evolutionary Biology studying red harvester ants. In 2023, he completed a post-doc at UC Davis. Daniel is exploring:
  • How can I live well?
    • How can I co-learn, research/collaborate, and serve all thinkers? With a special focus on all backgrounds (accessibility)? With a special focus on mature thinkers, advanced projects, shared realities? How can we understand how working and communicating relates to transcendental multiscale identities?
  • How can we have a real We?
    • How can I intra-individually, collaboratively, and in communities, support ... ? How can the quality, quantity, scope, meaning, impact of participation in communities of care/collaboration be expanded?
  • How can I propagate and perpetuate a creative, rigorous, modern research program/agenda with a focus on:
    • Active Inference. What kind of InferAnt am I and are We? How can I facilitate others to learn, research, and apply Active Inference?
    • Ants. How can the Ant Colony system be a model (like Drosophila, Linux kernel) for integrating e.g.
      • Global science, ecology, multi-omics (genomics, transcriptomics), cognitive modeling, Observers.
      • Category theory & strong relationing with other and general multi-agent ecosystems of shared intelligence, as in Toby St Clere Smithe's paper.
    • Synergetics. Physics / Engineering: How can Synergetics / Tensegrity be improved in clarity, rigor, and applicability today? How can we understand the analytical (e.g. vectorical, geometric, topological) and other (e.g. psychological, cognitive, metaphysical) aspects of Synergetics?
  • What are fundamental and theoretical underpinnings/mappings of Cognitive Security?
  • What are the cognitive aspects of rhetoric, generating/interpreting languages, multimodality, etc.
  • How do we bring together the material and the invisible?
  • Andrius is investigating, with Daniel's help:
    • How can we facilitate the collection and systematization of cognitive frameworks so that people look for an underlying reality, as with Wondrous Wisdom?
• Marcus Petz received his PhD in Social and Public Policy for his research in community currency for rural renaissance.
  • How can financial solutions serve both human community and natural world?
  • How can we turn around downward economic spirals in rural communities?
  • What is the process of syntropic finance by which there are financial solutions optimal for specific contexts?

I, Andrius Kulikauskas, offer a context of Wondrous Wisdom through my own ongoing investigations into absolute truth.

• Language of Wisdom is a bottom-up documentation of the cognitive frameworks of the perspectives by which we experience life, especially abstractly, as divorced from direct experience, and from accumulated assumptions, considering the limits of consciousness itself, and thereby, the possibilities of the conscious and the unconscious.
• Logos: God as Theory is a top-down interpretation of these frameworks in terms of God's investigations (whether, what, how, why there is God? respectively, as God, I, You, Other) and human's investigations (how to live as God? namely, through eternal life, wisdom, good will, God's will).
• Math 4 Wisdom is my work to identify those frameworks where they appear in the language of advanced mathematics. I present these findings in terms of '''three minds - the unconscious (which knows the answers), the conscious (which asks the questions) and consciousness (which relates them with investigations) - that can be observed in psychology, neuroscience, consciousness studies and related disiciplines.
• Landscape of Truth is my view on our Math 4 Wisdom community as a social experiment. We are applying knowledge usefully, as in peacemaking. We are learning to investigate alongside each other, leveraging the diversity in our relationships with truth, living in consciousness.
• Personal Growth is my concern to grow forever, learn forever, live forever as a person and as a leader.
• God's Investigations is my endeavor to recognize, engage and support God as an investigator.

I work at this wiki (in English) and also at www.ms.lt (in Lithuanian).

Wondrous Andrius

Thank you! for supporting Math4Wisdom through Patreon

• Sign up here!
• Thank you to Daniel Friedman, John Harland, Bill Pahl and 3 anonymous supporters!