Introduction E9F5FC

Questions FFFFC0

• View
• Edit
• History
• Print

Modeling the Self with Quantum Symmetries of Hamiltonians for Noninteracting Fermions

Hamiltonian

• The Hamiltonian is the self as the being conceived, which must be conceived again as the third mind in order to get back to the first mind.
• Hamiltonians are Hermitian.
• Hamiltonian is the self. It describes what it means to have a coherent self-identity that can evolve in time. It is the agglomeration of all of the dynamical possibilities for a system which can experience particular conditions.
• These Hamiltonians are maps between complex vectors spaces and so are the quantum symmetries. {$C$} and {$T$} are antilinear maps.
• Global constraint, imposing the Hermitian-ness, is love. How to understand the local constraint?
• The self is modeled by the Hamiltonian.
• The Hamiltonian models the self, thus not the being, but rather what it observes of itself, its personal context as such.
• The symmetry of a Hamiltonian indicates that the input states and output states, the creation operators and annihilation operators, the particles and the holes can be swapped. In this sense, the Hamiltonian, the self, is balanced.
• The Hamiltonians, going round the Bott clock, switch back and forth between unity and disunity of the self-as-being and self-as-context (where one is the conjugate transpose of the other). The {$2x2$} off-diagonal block form expresses their disunity and the other form variously expresses their unity. The oscillation is familiar from database systems where a data copy is presented to a user, who may then change it, and then that change has to be updated to the original database.
• Can think of the choosing of the basis as simplifying the Hamiltonian to having eigenvalues {$+1$} and {$-1$}, thus dividing the matrix into four blocks.
• A nonordinary symmetry on a Hamiltonian means that it has a context. Metaphysically, a context is very restricted because we can think of the context of the context, which inverts it. Inverting a context returns it to what is known ({$+1$}) or to its opposite, what is not known {$-1$}. The context functions like the dual of a vector space and so taking the dual of the dual takes us back to the vector space (the set of all possibilities that it could have satisfying the constraints) but here we end up with two options, not just one.
• Symmetries {$C$} and {$S$} presume the pairing of particles and holes. But also the distinction is presumed by the {$T$} symmetry {$1_{p,q}H=H1_{p,q}$}. Only the question of when {$p=q$} is undetermined.
• The presence or absence of anti-unitary symmetries is a matter of reality conditions on the block Hamiltonians (of the Hamiltonians on which the unitary symmetries hold).
• If {$H$} satisfies Schroedinger's equation {$H|\psi(t)\rangle=i\hbar \frac{d}{dt}|\psi(t)\rangle$}, then {$m=-iH$} satisfies {$m|\psi(t)\rangle=-\hbar\frac{d}{dt}|\psi(t)\rangle$} yielding {$|\psi(t)\rangle=e^{-mt/\hbar}$}.

Dynkin diagrams

• Transposing symmetries are the basis for counting, thus the symmetry of counting, as given by the Dynkin diagrams.
• Fermions are things that you can count, as they must all be distinct. And so they are related to the symmetries of counting.

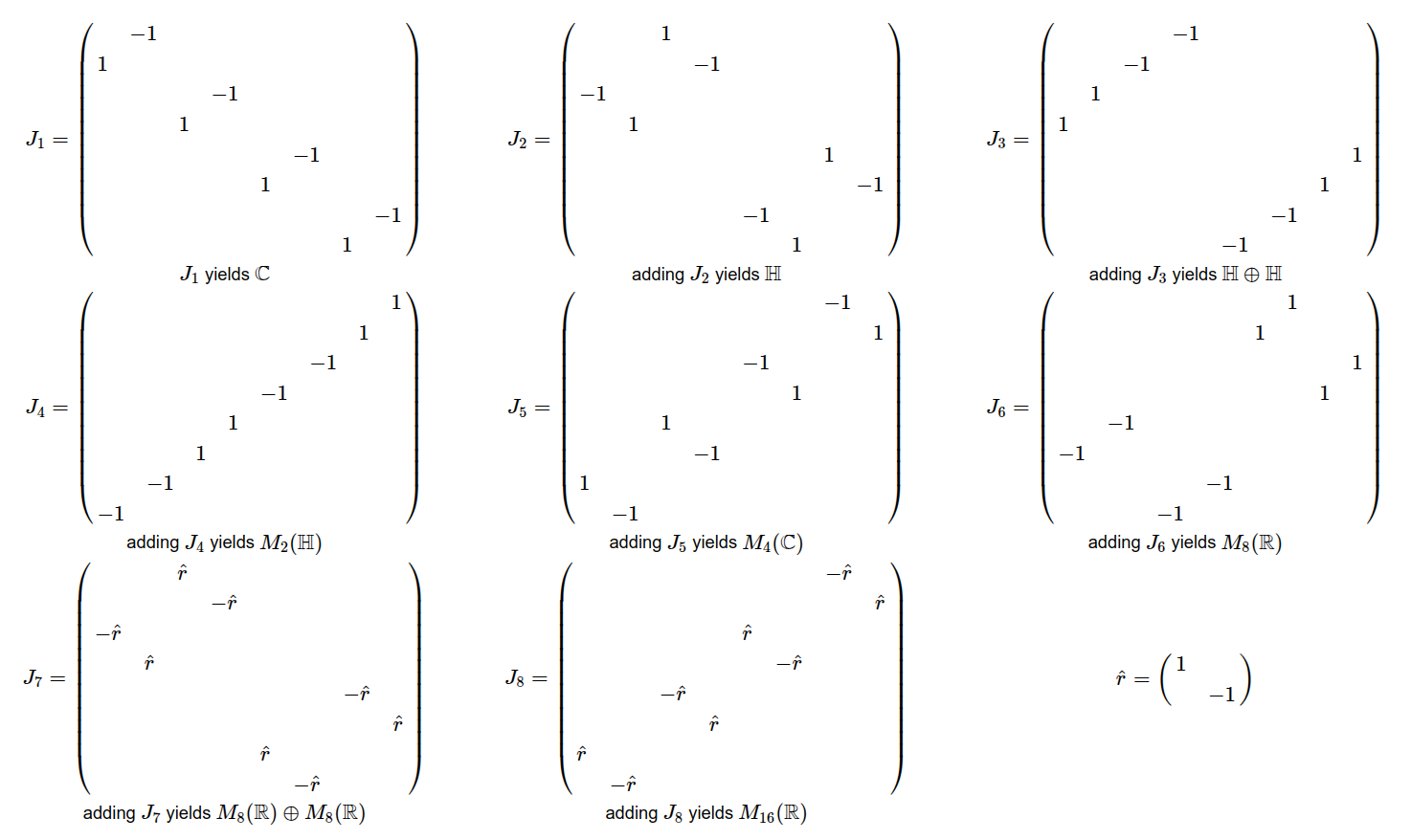
Linear complex structures

• The perspective is modeled by the linear complex structure {$J_k$}
• The pseudoscalar {$J_6J_5J_4J_3J_2J_1$} equals the building block for {$J_7$} and for {$J_8$}
• Symmetries are built up from the linear complex structures.
• Knowledge evokes the self. With the fourth perspective, we restrict the self to an eigenspace. The other eigenspace can be identified with the defined self, imposed by sublattice symmetry, and according with it, establishing its basis. Thus knowledge evokes the self and involves a latent perspective bigger than the self, through which the self can be understood.
• In Stone, Chiu, Roy, the antilinear maps {$\mathcal{C}H\mathcal{C}^{-1} = −H$} can be understood as real matrices with {$2\times 2$} antilinear blocks. They are given by complex matrices {$CH^∗ C^{−1} = −H$}.
• The {$m\in\frak{m}_i$} are commuting with {$J_1,\dots,J_m$} but anticommuting with {$J_{m+1}$}. This means that they branch away from those that commute with all {$J_i$}. Thus they are all disjoint. And the initial {$m\in\frak{m}_0$} are those that simply anticommute with {$J_1$}. What does it mean for them to commute with a mythical {$J_0$} and previous linear complex structures?

Lie group embeddings

• Two ways of looking at the Lie group embeddings
  • There is a linear complex structure {$J_i$} and the matrices it commutes with form a subgroup {$H$} of {$G$}.
  • There is a Lie algebra {$\frak{g}=\frak{h}+\frak{m}$} where {$[\frak{h},\frak{h}]\in\frak{h}, [\frak{h},\frak{m}]\in\frak{m}, [\frak{m},\frak{m}]\in\frak{h}$}, and {$\frak{m}$} are {$i\times$} the Hamiltonians (corresponding to the time evolution operators {$e^{iHt/ \hbar}$} in the unitary group), and {$G$} and {$H$} are the Lie groups corresponding to {$\frak{g}$} and {$\frak{h}$}.

The symmetric spaces form a sequence of order-parameter spaces that arise as we progressively break a large symmetry by introducing more and more symmetry-breaking operators. As a bonus, the matrices representing the symmetry-breaking operators will later serve as the building blocks of model Hamiltonians that yield all possible topologically non-trivial band structures.

• The {$O(n)\times O(n)$} and likewise stages mean that the number of positive energy states and negative energy states have to match up. This is the same as matching up what is known and what is not known, or being and not being. Consciousness is responsible for lining this up. And this allows us to proceed to the next stage.

Commutation

• Commutation of {$A$} and {$H$} means that {$A$} is constant in time. They can both be simultaneously diagonalised. As observables, they can be measured simultaneously. They share the same set of eigenstates and thus any state can be expanded as a sum of these.
• Physics Stack Exchange. Commuting with the Hamiltonian. An operator {$A$} that commutes with the Hamiltonian {$H$} is conserved. In the Heisenberg picture, {$\frac{dA}{dt}=-\frac{i}{\hbar}[A,H]$}. The Hamiltonian establishes the framework for all that is conserved over time. The Hamiltonian is the infinitesimal generator of time translation. Compare with Ehrenfest theorem and {$\frac{d}{dt}\langle A \rangle = \frac{1}{i\hbar}\langle [A,H] \rangle + \langle \frac{\partial A}{\partial t}\rangle$}.
• The measurement yielding an eigenvalue is more a fact about the measurer, how they approached the system, rather than the system measured.

Octonions

• The diagonal matrices in my octonion interpretation are straightening out the eigenspaces so that they are degenerate.

Insulators and superconductors

• Similar to bioelectric fields - surface conduction

Quantum symmetries

• The perspective alternatives between {$H$} (stepping in) and {$H^*$} (stepping out) by {$H^*J_k=J_kH$}
• Qualia are given by the unconscious.
• Closing the gap (between positive and negative energy levels) changes the insulator by making it into a conductor
• A division of everything is a mental context. It may be defined by the relevant quantum symmetries, in that they are contexts.

Time reversal

• Whereas accessibility {$T$} encodes {$\mathbb{C}+e\mathbb{C}$} and this {$e$} can be understood as {$T$}.
• Accessibility (time reversal) moves you back and forth within your world, manifesting two-track attention, thus what is knowable.
• Anticommutation means that {$\frac{dA}{dt}=\frac{2iH}{\hbar}A$} which implies {$A=e^{\frac{2iH}{h}t}$}, the time evolution operator, the propagator, but with time {$t$} reversed.

Anticommutation

• From {$HA+AH=0$}, you can directly show that non-zero eigenvalues of the Hamiltonian come in pairs: If {$\psi_n$} is an eigenstate for eigenvalue {$n$}, then {$A\psi_n$} is an eigenstate for {$−n$}. Thus {$A$} takes you from positive eigenstates to negative eigenstates and vice versa.
• If {$A$} is unitary and anticommutes with the Hamiltonian, this implies a symmetry in the energy spectrum: for every eigenstate {$|E\rangle $} of {$H$} with eigenvalue {$E$}, there exists another eigenstate {$A^{-1}|E\rangle$} with energy eigenvalue {$-E$}.
• Detailed balance - at equilibrium, each elementary process is in equilibrium with its reverse process - is expressed by the geometry of a symmetric space.
• Time reversal restricts unitary matrices so that they are not orthogonal or they are not symplectic.

Charge conjugation

• Division superalgebras extend inaccessibility {$C$} for it encodes {$\mathbb{R}$} ({$C^2=1$}) and {$\mathbb{H}$} ({$C^2=-1$}) and there is also no symmetry which encodes {$\mathbb{C}$}.
• Inaccessibility (charge conjugation) takes you to another world but in the opposite time direction, thus emphasizing that world's inaccessibility, manifesting a one-track attention, thus what is unknowable. (What do the directions of time mean here? The ability to go back and forth, as with the fivesome.)
• Charge conjugation yields orthogonal or yields symplectic matrices.

Sublattice symmetry

• Balancing prejudices (first mind) and preconceptions (second mind) gives us the absolute frame, the third mind. Letting go of prejudices and preconceptions gets us to the absolute frame by itself.
• Definability (sublattice) distinguishes between particles that go to holes and that go to negative holes. Unconsciuos refers to the knower and conscious to the not-knower.
• The Bott clock oscillates between not having the sublattice symmetry (and the eigenvalues +1 and -1) or having it.

Combining linear complex structures and quantum symmetries

• Walking along the clock, except for the initial interpretation of {$C$}, then we have to build the symmetries from the single operators {$J_k$} (why?) and so first they must be squaring to {$-1$} and so first they must be conscious and only then can the symmetries be unconscious. This is the primacy of the conscious mind for internal experience.

Facts

• When {$H_k=J_1m_k$}, we have {$J_1$} and {$J_{k+1}$} commute with {$H_k$}, and {$J_2,\dots,J_k$} anticommute with {$H_k$}.
• When you perform a quantum mechanical measurement, you will always measure an eigenvalue of your operator, and after the measurement your state is left in the corresponding eigenstate. The eigenstates to the operator are precisely those states for which there is no uncertainty in the measurement: You will always measure the eigenvalue, with probability {$1$}. An example are the energy-eigenstates. If you are in a state {$|n\rangle$} with eigenenergy {$E_n$}, you know that {$H|n\rangle=E_n|n\rangle$} and you will always measure this energy {$E_n$}.
• The antilinearity of {$\hat{\mathcal{T}}$}, with {$\hat{\mathcal{T}}\hat{H}\hat{\mathcal{T}}^{-1}=\hat{H}$}, acting on {$\hat{\mathcal{U}}(t)=e^{it\hat{H}}$}, yields time reversal {$\hat{\mathcal{T}}\hat{U}\hat{\mathcal{T}}^{-1}=\hat{U}(-t)$}.
• Polar decomposition of a matrix {$A=UP$} in terms of a unitary matrix {$U$} and a positive semi-definite Hermitian matrix {$P$}.
• Nambu mechanics considers multiple Hamiltonians.
• An anti-symmetric matrix {$M$} (from a Lie algebra) can be decomposed {$M=M_a+M_s$} in terms of an anti-symmetric matrix {$M_a=\frac{1}{2}M-M^T$} (from a Lie subalgebra) and a symmetric matrix {$M_s=\frac{1}{2}M+M^T$}. The symmetric matrix yields, upon exponentiation, the time-evolution operator in the coset space, which is a symmetric space.
• Quantized Hall effect - adding a hole in the insulator
• Time reversal - no magnetism.
• Two classes of time reversal symmetric insulators - in two dimensions: no edge states vs. quantum spin Hall insulator (edge states).
  • Three dimensions: no surface states vs. protected surface conductance
• Can add a crystal reflection symmetry.

Ideas

• The symmetries of context.
• Lurking in the heart of math are the symmetries of math itself.

Sources

• Ben Goertzel. From Complexity to Creativity. Chapter 8. The Structure of Consciousness.