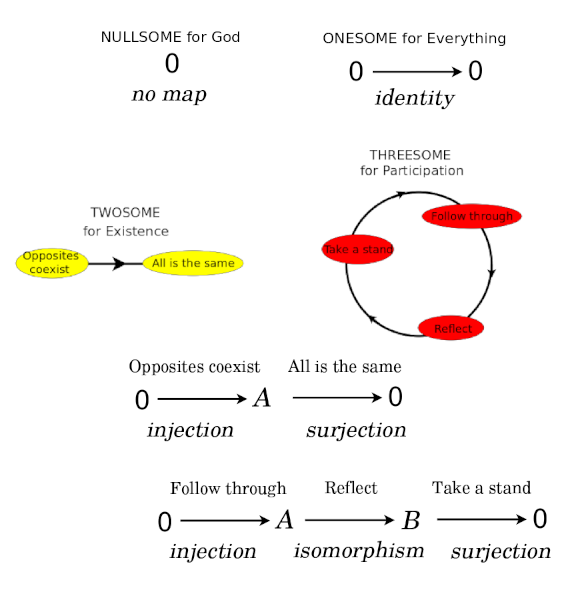
Introduction E9F5FC

Questions FFFFC0

• View
• Edit
• History
• Print

Bott Periodicity Models Divisions of Everything

Wondrous Wisdom

Perspective

• Think of a perspective (a circle) as a saccade.
• The circle {$U(1)$}, key for quantum symmetry, models a perspective, is the source of rotations, the foundation of geometry.

Three minds

• +1 Add one operator. Impose linear complex structure. I. Unconscious.
• +2 Add two mutually anticommuting operators. Impose quaternionic structure. You. Conscious.
• +3 Add three mutually anticommuting operators. Impose split-biquaternionic structure. Other. Consciousness.
• Rulead space generated by three minds, the three possible rules on the eight cycle.
• Super division algebras relate the two minds, unconscious and conscious, as odd and even subalgebras. See Todd Trimble's notes. I want to relate this to quantum symmetries.

Reflection. Unconscious and conscious.

• Complex conjugation is an example of reflection.
• Reflection is not commutative with regard to a linear complex structure.
• Noncommuting means incompatible frameworks. So rotations and rotoreflections are incompatible. Unconscious and conscious are incompatible. But there is an isometry between unconscious and conscious.
• Linear (this is this; that is that) and antilinear (this is that; that is this).
• what is real is unreflected
• Knowing becomes the past (decreasing slack). Not knowing opens up the future (increasing slack).
• Odd is reflective, switching spaces to acknowledge the reflection. Even is nonreflective (raw).
• A gapped Hamiltonian can be understood as {$H\neq 0$} separating and distinguishing {$H>0$} (conscious) and {$H<0$} (unconscious). This establishes a change in perspective, stepping in and stepping out.
• {$-I$} as reflection. {$J_1J_2=-J_2J_1$} One way is the reflection of the other.

Chain of perspectives

• We can carve up mental space from either end, in the (+1) and (-1) directions, or both ends (+2), arriving at {$Cl_{4,0}\cong Cl_{0,4}$}. How to understand (+3)? Compare Clifford algebras with chain complexes.

` Context

• Basis is a context, supplies a context, provides a context. The number of bases involved is the context.

Two cycles of Clifford algebras

• Think of Bott periodicity as starting with (3+3)=humanity in one eight-cycle and continuing with +1, +1, +1 given by charge conjugation, and +1, +2, +3 in the other eight-cycle.

Shift in perspective

• Linear complex structure {$J_i$} is a perspective. A shift in perspective from {$J_i$} to {$J_j$} is their product {$J_iJ_j$}. Together they define a quaternionic structure.
• Doubling, halving, dividing a perspective (a space, a module) into two perspectives, yielding a perspective on a perspective.

Recurring activity and structure

• The essence of Bott perioidicity is relating (in terms of their actions, their symmetries) a (one-dimensional) circle {$U(1)$} (embedded in two dimensions) and {$\mathbb{Z}_2\times\mathbb{Z}_2$} (two zero-dimensional circles embedded in two dimensions)(or a vertical strip with top and bottom, front and back)

Perception-action loop

• The Clifford algebra expression {$\cos\theta e_1+\sin\theta e_2$} for the pin group {$Pin_\pm(2)$} may express the perception-action loop. It is periodic like a photon.

Eight contexts

• Renormalization group: Block spin This model is relevant when everything has only one parent, when the matrices are sparse and so there are local collections as to causality. Similarly, the chance of two neurons being connected is very small. Relate this to Bott periodicity. Each level increases or decreases the level of detail. But eight levels of detail (eight contexts) are all that you can distinguish and then you would just repeat.

Chomsky hierarchy

• In Todd Trimble's classification of super division algebras, consider how they relate to the Chomsky hierarchy. In particular, for {$H+He$} we have {$hex=exh$} as with a linear Turing machine by which we could have {$hhhhhhex=exhhhhhhh$}. For {$C+Ce$} we have {$ce=e\bar{c}$}. This means that (when {$|c|=1$}) we have {$e=cec$} as with a pushdown automata. For {$R+Re$} we have {$re = er$}. If {$r=1$}, then {$e=er$}, as with finite automata. So it's true modulo real scalars. And then we should have a collapse {$e=$} disappears, as with {$C\ell_{\pm 4}$} when {$H$} is just the even part.

Contradiction

• Think of Bott periodicity as 8-2=6 where the -2 subtracts the complex Bott periodicity, which represents God and good in 6+1+1 and which creates the context for contradiction, making for the Bott cycle.

Divisible by 8

• Over the reals the Clifford algebras {$Cl_{n,0}$} and likewise {$Cl_{0,n}$} are matrix superalgebras if n is divisible by 8. Their elements are either even (diagonal blocks) or odd (off diagonal blocks). Calculate this explicitly.

Divisions of everything

• The three-cycle is a parity operator (for space) which establishes supersymmetry. Space and time together define the foursome.
• Think of divisions of everything as an adjoint functor to the application of a linear complex structure on a symmetric space.

Channels in reservations

• 0 channels {$\mathbb{R}\oplus 0$} nullsome (the zero)
• 1 channel {$\mathbb{R}\oplus\mathbb{R}$} onesome
• 2 channels {$\mathbb{C}\oplus\mathbb{C}$} twosome
• 3 channels {$\mathbb{H}\oplus\mathbb{H}$} threesome
• {$(\mathbb{H}\oplus\mathbb{H})\oplus (\mathbb{H}\oplus\mathbb{H})$} foursome {$\mathbb{H}\oplus 0$}

Father, Son

• Orthogonal add a perspective (Father), symplectic subtract a perspective (Son).
• John Baez's comment about 4 dimensions being most interesting because half-way between 0 and 8. The Son turns around and reverses the Father.

Going beyond oneself

• In Bott periodicity, the going beyond oneself (by adding perspectives) and the going outside of oneself (by subtracting perspectives) is, in mathematics, extended to all possible integers, and thus the two directions are related in the four ways as given by the four classical Lie algebras, including gluing, fusing, folding.
• In the eight-cycle of divisions, the going beyond oneself and the going back outside oneself are reminiscent of spinors like electrons.
• The flip side of going beyond yourself - if you can add perspectives, then you can substract perspectives - on the flip side. Thus nullsome and foursome model the extremes: nullsome models the void of everything, foursome models the point of nothing. Thus adding a perspective takes us from the indefinite to the definite and back again. The three operations +1,+2,+3 make for a three-fold braid.

Accessible, inaccessible, definite

• Goedel's incompleteness theorem. There is irrelevant, inaccessible knowledge, such as that which describe different implementation of equivalent rings (for Bott periodicity) where the equivalence means that they have the same (isomorphically, structurally) representations.

---

Squaring to {$-1$} or {$+1$}

---

When generators {$e_k$} square {$e_k^2=1$}, then this directly yields a split of the vector space {$V=V_+\oplus V_-$}, and so the Clifford algebra is {$Cl_{1,0}=\mathbb{R}\oplus \mathbb{R}$}. Whereas if the generators {$e_k$} square {$e_k^2=-1$}, then we have to wait until we have the product of three generators squaring {$(e_1e_2e_3)^2=1$} to split the vector space, in which case the Clifford algebra is {$Cl_{1,0}=\mathbb{H}\oplus \mathbb{H}$}. Thus squaring to {$-1$} yields first internal structure, and only then external structure. Whereas squaring to {$+1$} yields first external structure, and then internal structure. They coincide with {$Cl_{4,0}=Cl_(0,4)=M_2(\mathbb{H})$}.

---

Divisions of Everything

---

A perspective is modeled by a linear complex structure {$J_k$}.

• These act on an orthogonal group {$O(16r)$} where {$r$} is an integer. {$J_k^2=-1$}.

Distinct perspectives {$J_j$} and {$J_k$} are mutually anticommuting linear complex structures, which is to say, {$J_jJ_k=-J_kJ_j$}.

A division of everything is modeled by a Clifford algebra {$Cl_{0,k}$} generated by mutually anticommuting {$J_1,J_2,\dots ,J_k$}.

As we apply these structures sequentially to {$O(16r)$}, we can ask, which matrices they commute with, and which do they not commute with? In general, it seems that they commute with those which have no contextualization, and they do not commute with those which have a contextualization. But this notion changes as we keep applying a new, mutually anticommuting structure.

Mental reflection is modeled variously, as inversion, as reflection, as complex conjugation, as antilinearity, as that which is culled away because of noncommutativity.

---

Removing the contextualized

---

The unfolding of the divisions of everything can be thought of as a process of continuously removing contextualized knowledge (what is not known) and restricting to actual raw experience (what is known). At a certain point this ends up restricting to a smaller and smaller portion of the vector space.

Think of {$O(n)$} as describing experience. Applying a linear complex structure yields {$U(n)$} as uncontextualized, unreflected, known, raw experience, separating away the unknown, contextualized, reflected experience. Then further apply a second linear complex structure yielding {$Sp(n)$} as unreflected unreflected experience, knowledge, throwing away the reflected unreflected experience. Apply a third linear complex structure yielding {$Sp(n)\times Sp(n)$} as unreflected unreflected unreflected experience, twofold knowledge, which is to say, knowledge in two forms, Unconscious and Conscious, yet unrelated. These take us from {$O(n)$} to {$U(n)$}, from {$U(n)$} to {$Sp(n)$}, from {$Sp(n)$} to {$Sp(n)\times Sp(n)$}.

• {$O(n)$} all are known.
• {$U(n)$} all are known as knowers, beings, witnesses.
• {$Sp(n)$} all are not known as knowledge. (Witness to a witness.)

Then the split-biquaternionic structure equates isomorphically the two spaces, two kinds of knowledge, one reflecting the other, so there is no more throwing away the reflected. Then they develop separately and finally they are equated, identified as one and the same.

Experience thus includes three levels of reflection which are stripped away. The reflection at each stage takes on different forms as the rotoreflections, the antilinear operator and the break down of the vector space {$V=V_+\oplus V_-$}. But then those two subspaces get equated so there is no more stripping away, we have hit bottom. This yields a three-cycle that returns back to where we started.

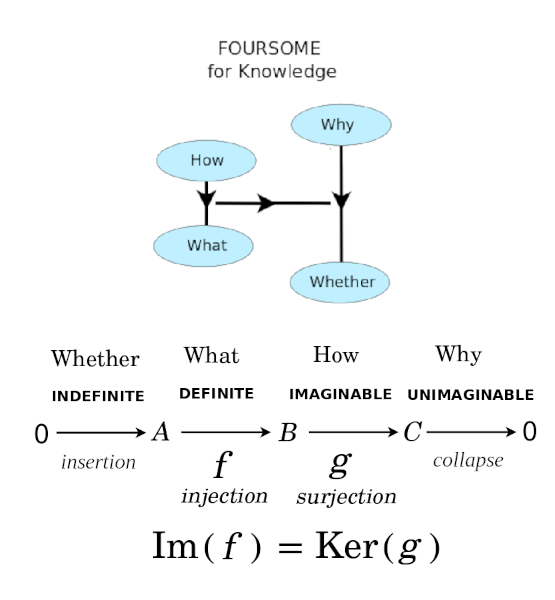
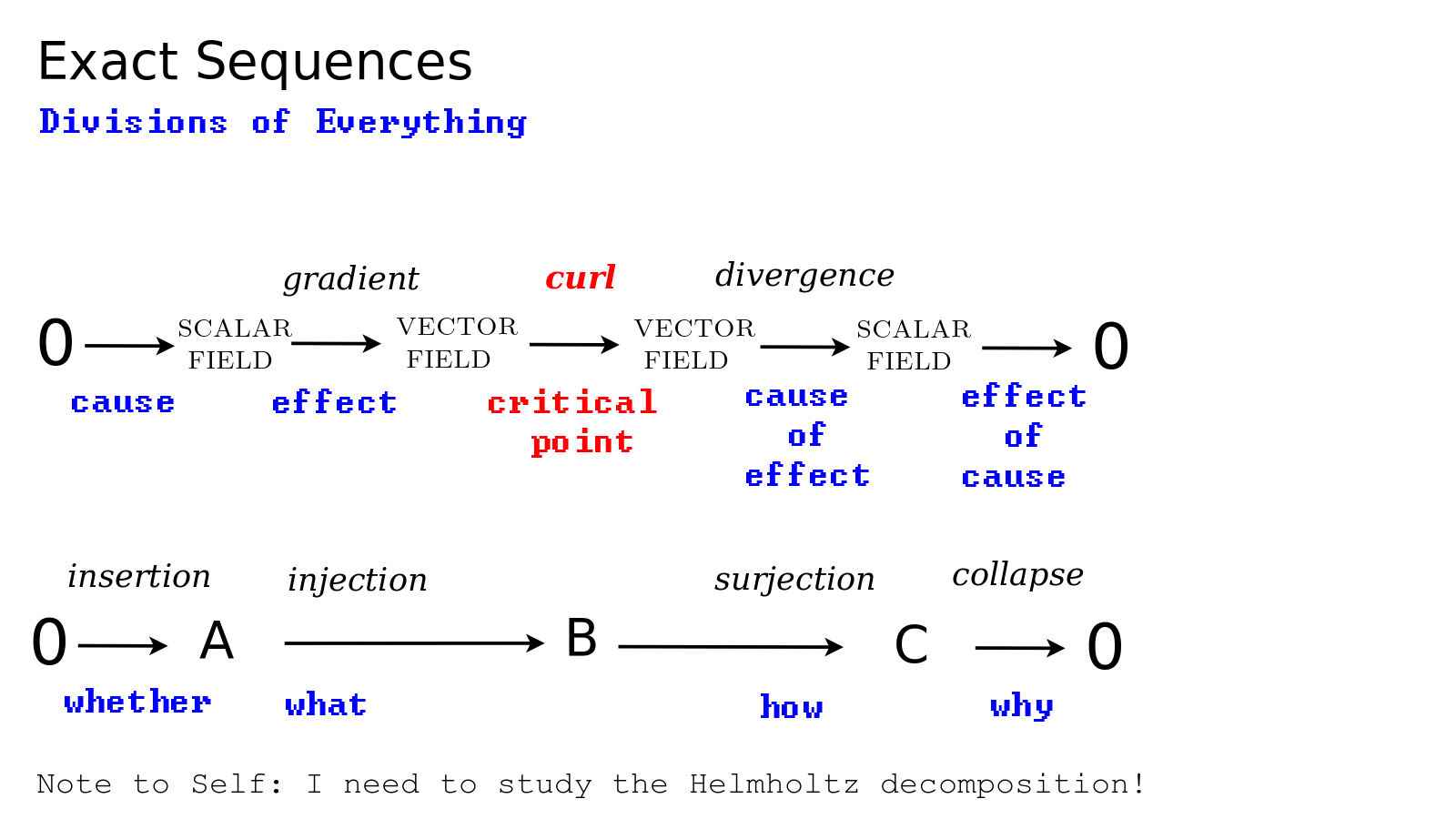
This bottoming out of reflection, with the three-cycle, grounds 3 dimensions of space and the fourth dimension of time, which refers back to the first dimension and functions as a clock marking time on the three-cycle. So we experience time as lived internally. This is given by the fivesome, where the two axes relate whether, what, how, why, one of which is time. The present is the whole of it all.

The gap evolves further with morality where there is a conscience, a concientious perspective upon the present. And this is one of three pairs defining perspectives, which by conscientiousness are equivalent to each other, by a three-cycle. Then further the gap evolves with the supposition of a hypothesis, where there exist known and unknown side-by-side. But this collapses when the hypothesis is affirmed.

The contradiction of the eightsome: all are known and all are not known. Unconscious: {$O(n)$} all are known. Conscious: {$O(n)$} all are not known. The sevensome keeps them separate but the eightsome equates them, gives them opposite meanings. But the sevensome relates exists a known and exists an unknown. How is that interpreted here?

Comparing {$O(n),U(n),Sp(n)$}. Comparing complex and real Bott periodicity.

Beings have linear complex structure, knowledge has quaternionic structure.

---

{$Cl_{0,0}=\mathbb{R}$} Nullsome. {$O(16)$} to {$O(16)$}

---

{$Cl_{0,1}=\mathbb{C}$} Onesome. {$U(8)$} to {$O(16)$}

Any linear complex structure functions as a perspective.

---

{$Cl_{0,2}=\mathbb{H}$} Twosome. {$Sp(4)$} to {$O(16)$}

Two mutually anticommuting linear complex structures define a quaternionic structure.

A product of two linear complex structures functions as a shift in perspective.

---

{$Cl_{0,3}=\mathbb{H}\oplus\mathbb{H}$} Threesome. {$Sp(2)\times Sp(2)$} to {$O(16)$}

Pseudoscalar squares to {$+1$}. {$(J_1J_2J_3)^2=1$}

We have that {$J_1J_2J_3=J_2J_3J_1=J_2J_3J_1$}.

We also have that {$J_1J_2J_3$} splits {$V=V_+\oplus V_-$} where {$J_1J_2J_3v_+ = v_+$} for {$v_+\in V_+$} and {$J_1J_2J_3v_- = -v_-$} for {$v_-\in V_-$}.

{$J_1J_2v_- = J_3v_-,\; J_2J_3v_-=J_1v_-,\; J_3J_1v_-=J_2v_-$}

A product of three linear complex structures breaks up the vector space into two eigenspaces, {$S_+$} and {$S_-$}.

Three mutually anticommuting linear complex structures define a split-biquaternionic structure.

---

{$Cl_{0,4}=M_2(\mathbb{H})$} Foursome. {$Sp(2)$} to {$O(16)$}

{$J_3J_4$} sets up an isometry between {$V_+$} and {$V_-$}.

---

{$Cl_{0,5}=M_4(\mathbb{C})$} Fivesome. {$U(2)$} to {$O(16)$}

{$J_1J_4J_5$} commutes with {$J_1J_2J_3$} and acts within {$V_+$} (or {$V_-$}) and divides it into mutually orthogonal eigenspaces {$W_\pm$} with {$W_-=J_2W_+$}. {$J_2$} interchanges the {$1$} and {$j$} so we are left with those matrices that only mix {$1$} and {$i$}, thus are complex.

Can we think of the new operators as developing the gap in between? Or can we think of them as appearing on either end of the chain?

---

{$Cl_{0,6}=M_8(\mathbb{R})$} Sixsome. {$O(2)$} to {$O(16)$}

{$J_2J_4J_6$} commutes with {$J_1J_2J_3$} and with {$J_1J_4J_5$} and acts within {$W_\pm$} and splits it into {$X_\pm$} such that {$X_-=J_1X_+$}. {$J_1$} acts as {$i$}, thus we are left with those matrices that are without {$i$}.

---

{$Cl_{0,7}=M_8(\mathbb{R})\oplus M_8(\mathbb{R})$} Sevensome. {$O(1)\times O(1)$} to {$O(16)$}

{$J_1J_6J_7$} commutes with {$J_1J_2J_3$}, {$J_1J_4J_5$}, {$J_2J_4J_6$} and splits {$X_+$} into subspaces {$Y_\pm$}

---

{$Cl_{0,8}=M_{16}(\mathbb{R})$} Eightsome. {$O(1)$} to {$O(16)$}

{$J_7J_8$} commutes with {$J_1J_2J_3$}, {$J_1J_4J_5$}, {$J_2J_4J_6$} but anticommutes with {$J_1J_6J_7$} and thus sets up an isometry between {$Y_+$} and {$Y_-$}. Are there circumstances where this could be considered contradictory?

Consider flavors of Bott periodicity where this collapses back to the nullsome. In particular, consider Morita equivalence. Yet Morita equivalence equates all matrix algebras of a division algebra, thus equates too many structures.

---

Products of perspectives

---

{$J_\alpha J_\beta$} relates Unconscious and Conscious.

{$J_\alpha J_\gamma J_\delta$} divides the vector space into worlds where {$J_\alpha$} and {$J_\beta$} are experienced as How {$-v\rightarrow v$} and What {$v\rightarrow v$} (as in the How and What of an arrow by the Yoneda embedding). Whereas {$J_\gamma J_\delta$} is their framework which is not experienced but grounds the experience as Why and Whether.

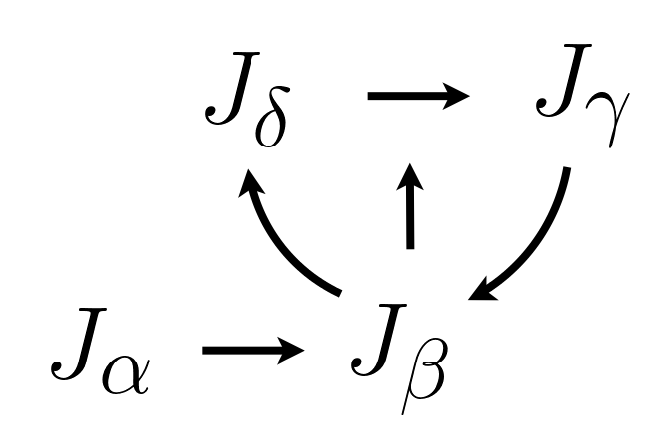
The homotopy groups {$\mathbb{Z}_2$} link the second mind with the first mind, and the third mind with the second mind.

The fourth mind is linked to itself, yielding {$\mathbb{Z}$}. So is the eighth mind.

---

Modeling physical systems

---

• Cohl Furey. Bott Periodicity Particle Physics

Modeling biological systems

Krebs cycle.

Bott periodicity. Sulfur as an eight-cycle. The origin of life.

• https://en.wikipedia.org/wiki/Octasulfur
• https://en.wikipedia.org/wiki/Iron%E2%80%93sulfur_world_hypothesis
• Bott periodicity 8=0 could be the basis for reproduction.

---

Ideas

---

• We have {$O, O\times O, O$} where in one direction we have the nullsome, and in the other direction we have the sevensome = {$-1$}.
• This describes the operation +1 as given by the mind and its counterquestions. The operation +2 maps on circles yielding Mobius transformations. So I should study how the six transformations of the boundary yield expectations and two ways of looking at them in terms of Unconscious and Conscious.
• {$O(16)$} is Father, {$U(8)$} is Son, {$Sp(4)$} is Spirit.
• Divisions of everything are made up of perspectives which are reflections of raw experience, that which was cast away, thus which fills the gap between {$O(n)$} and the embedded Lie group.
• Grassmannian chooses vector subspaces, thus models choice. Recall {$F_1$} models God.
• The vector space gets repeatedly divided up into two halves, unreflective (eigenvalue 1) and reflective (eigenvalue -1).
• The foursome combines a shift in perspective in unreflected {$V_+$} (where the three-cycle turns in one direction) with a shift in perspective in reflected {$V_-$} (where the three-cycle turns in the opposite direction).
• A transpose is the reflection of indices {$M_{a,b}\rightarrow M_{b,a}$}. An inverse is the reflection (inversion) of action.
• Raw experience as God and human is related by the operation +4, complex Bott periodicity.
• Every perspective divides up space into raw, immersed, direct, "stepped in" experience and refected, removed, distant, "stepped out" experience.
• The relevant Lie groups are all rotations about a fixed origin. That fixed origin represents a universal, absolute perspective, God's perspective upon everything, God's knowledge of everything.
• Divisions of everything are perhaps chopping up a sphere where the sphere is everything also circle folding
• Bott periodicity should be related to the collapse of the eightsome into the nullsome, and thus the definition of contradiction
• Perspective arises because of base point - there is a fixed point for the isometries. We are that fixed point.
• Understand the dimensions of a Lie group as perspectives. And look at Lie groups as rotations of a sphere.
• The widgets at the end of the Dynkin chain allow for turning around and thus for ambiguity in the understanding of the perspective of the chain and thus they can be understood as divisions of everything. And this should relate to Bott periodicity.
• ketverybė: H, nulybė: R
• 2-periodicity: Dievas - gerumas - Dievas
• sukeisti buvimą ir nebuvimą, tapimą ir netapimą
• 10 = 4+6 = 4+(4+2) = 8 + 2 (2 tai laisvumo atvaizdai)
• Z 0 Z 0 Z 0
• Z 0 (replace Z 0 with Z2 Z2 particle) Z 0 (replace Z 0 with 0 0 hole)
• 8 external dimensions (adding 4 dimensions or +2 or +3)
• internally expressed dimensions - adding integrity
• same pattern reversed internally
• Equivalence up to isomorphism is relevant for "user requirements" as opposed to "material implementation". This is relevant for Bott periodicity.

Bott periodicity provides order to the homotopy groups of spheres and that reflects that we are left with Consciousness when we unplug the Unconscious and likewise unplug the Conscious. So the relation between n and m is the relation between the Unconscious and the Conscious and their content.

Bott periodicity expresses the symmetry of mathematics

• compare this with how Lie algebra root systems express the symmetry in counting forwards and backwards, for example, in one direction {$e_i-e_j$} and in the opposite direction {$e_j-e_i$}.

In Bott Periodicity, the matrix representations are related:

• {$\mathbb{Z}_2$} as a product (limit) expressing external relationships {$\begin{pmatrix}A & \\ & B \end{pmatrix}$}
• {$\mathbb{Z}$} as a sum (colimit) {$A+B$} and {$A-B$} in terms of internal structure
• {$0$} representations are the same size. What is the significance?

Loop spaces

• Think of loopspace as expressing a space for learning.
• Loop - open arc - perspective - defines inside vs. outside - the ambiguity of a point.

Complex Bott periodicity, which relates U(n) and U(n+m)/U(n)xU(m), and goes back and forth between them, suggests that real Bott periodicity goes back and forth between O(n) and O(n+m)/O(n)xO(m). In one direction there is one step but in the other direction there are seven steps.

In Bott periodicity, {$\mathbb{Z}_2$} may count the unconscious and the conscious. They are the two pieces of {$O(\infty)$}. The homotopy groups explain the different ways of relating them.

A possible interpretation of the sequence. {$\mathbb{Z}$} expresses a hole as with the threesome and the sevensome. {$\mathbb{Z}_2$} describes the nullsome and the onesome.

• Three minds are three shifts adding 1, 2, 3 dimensions in the Bott clock shift.

Raw experience is the nullsome.

Bott periodicity models the inherent contradiction in thinking. Thinking (reflection, contextualization) leads to a contradiction. The three-cycle arises when focused on half of the mind, the unreflected, uncontextualized half, as we discard, reject the other half.

• realusis Bott periodiškumas: esmė yra sąmoningumas +3, ryšyje su proto būsenomis
• kompleksinis Bott periodiškumas: ryšys su pačiu žmogumi, su jo būkle. Išsako Dievo gerumą.