Introduction E9F5FC

Questions FFFFC0

• View
• Edit
• History
• Print

Quantum Symmetries

Strategy

My strategy is to

• check if {$J_7$} and [$J_8$} are algebraically independent of {$J_1,\dots, J_6$}
• follow the Stone-Roy-Chiu recipe to see if I can make sense of the restrictions on the spaces
• try to use the recipe to make sense of {$J_7$} and {$J_8$}
• try to calculate {$J_9$} and compare it with {$J_1$}
• compare my calculations of the {$m$} with the answers for the Hamiltonians
• understand how the absolute frame gives meaning to the distinction between real and imaginary numbers
• understand the origin of the natural bases for the symmetries, why they are natural for each symmetry
• investigate how the bases change in going from relative to absolute and back
• understand how the meaning of conjugation changes as we go from an absolute S symmetry {$1_{p,q}H1_{p,q}=-H$} to a C or T symmetry relating {$H^*$} and {$H$}
• understand how, in Stone-Chiu-Roy, the meaning of "i" changes as a {$2\times 2$}-block matrix and as an imaginary scalar
• understand how this relates to linear complex structures {$J_k$} but also {$iJ_k$} in the complex case
• consider a perspective as a change of basis between {$H^*$} and {$H$}, stepping in and stepping out
• consider how the Hamiltonian can be thought of as carved up into pieces, domains for perspectives
• understand how the linear complex structures {$J_i$} arise, first as {$\mathbf{U}_T$}, anticommuting with the Hamiltonian, and then as the basis gets redefined, and the earlier {$J_i$} now commute with the Hamiltonian, understand how they get redefined
• consider how the notion of a perspective may get redefined upon crossing the mirror {$L$}
• understand this in terms of Moore's bigraded representations of Clifford algebras
• understand this in terms of super division algebras
• interpret what it means to have a perspective by considering how we go from the (relative) nullsome the (absolute) onesome
• interpret what it means to have a shift in perspective by considering how we go from the (absolute) onesome to the (relative) twosome

And then further

• make the quantum symmetries intuitively clear
• show how that is reflected in the Hamiltonians
• explain how the linear complex structures take us through the Hamiltonians
• consider how one Hamiltonian relates to the next Hamiltonian
• explain how the linear complex structures take us through combinations of symmetries

Ideas

• Shifts in perspective may be given by total or partial isometries inherent in the {$J_k$} with respect to each other. These total or partial isometries are evident from the off-diagonal blocks. Even {$J_1$} has a perspective upon itself within the off-diagonal of its {$2\times 2$} building block.
• For Hermitian matrices, such as Hamiltonians, the conjugate of the matrix (a globally established, algebraic characteristic of the entries) equals the tranpose (a global, external characteristic of the matrix, which encodes the local inversion of the relationship {$i\rightarrow j$}).
• Consider in terms of dimensions, what we are keeping and what we are removing, and how they fit together.
• Think of the symmetries, and the definition of complex conjugation, as depending on whether the complex numbers are expressed intrinsically, algebraically {$a+bi$} or extrinsically as {$2\times 2$} matrices. Perhaps the symmetries takes us back and forth between these two understandings. Whether when we walk around the Bott clock we may be presuming an extrinsic understanding and then running into collapse.
• The Clifford algebras expressing the super division algebras, yielding {$Cl_{\pm}=M_2(\mathbb{H})$}, seem to match the entries of the Hamiltonian matrices, notably the reals and the quaternions.
• Consider the Jacobi identity as a basis for three minds in considering the Lie algebra decompositions.
• Complex Bott periodicity shows that its simply a matter of Hamiltonian being its conjugate transpose, whether it is a one state {$1\times 1$} relationship or two state {$2\times 2$} relationships. That brings to mind calculating independent dimensions of the Lie groups because you have on-diagonal (self-relationship) and the off-diagonal (which is a two-step relationship).
• From the point of view of quantum symmetries, and the Hamiltonian, it it the unitary Lie algebra that is of interest. That is why the Clifford algebras go plus and minus with regard to that. In the case of the real Bott periodicity, they don't see that perhaps, they are based on the orthogonal group.
• How the symmetry progresses around the Bott clock. It makes two copies of the Hermitian and its conjugate transpose, then puts them together and breaks them apart again. That is like fusing the two minds and then separating them, as if they are one, and then they are distinct. The odd stages are distinct, and they are not in sync properly. Whereas the even divisions are considered as in sync and can be thought of in terms of the third mind. You are oscillating between the unity of the mind and the disunity of the mind.
• The bra-ket notation is the basis for why a Hamiltonian is equal to its conjugate transpose with regard to the sesquilinear norm. It is related to the idea of a dual vector space, a context of a context meaning the same as the original thing.
• In complex Bott periodicity, no frame goes to double frame because it is based on {$iJ_1$}, which has two tracks. Whereas in real Bott periodicity, one frame goes to double frame because it is based on {$J_1$}, which has one track.
• The twosome, threesome, foursome are fundamental building blocks because they manifest consciousness and not unconsciousness.

---

---

---

---

The Hilbert space

Our Hilbert space has a basis which includes a vacuum state {$|0\rangle$}, {$L$} single particle states {$|1\rangle,\;\dots\;,|L\rangle$}, {$L$} single hole states {$|2\rangle|3\rangle\cdots|L\rangle,\dots,|1\rangle|2\rangle\cdots|L-1\rangle$} and a fully filled state {$|1\rangle|2\rangle\cdots|L\rangle$}. This is understood within a larger Hilbert space with states corresponding to {$2$} through {$L-2$} particles but these do not interest us.

Creation {$\psi_i^\dagger$} and annihilation {$\psi_i$} operators act on these states. We need them to act in pairs so that we respect the grading. These operators anticommute whereby {$\psi_i\psi_j=-\psi_j\psi_i, \psi_i^\dagger\psi_j^\dagger=-\psi_j^\dagger\psi_i^\dagger$} and also {$\psi_i\psi_j^\dagger = -\psi_j^\dagger\psi_i$} when {$i\neq j$} but {$\psi_i\psi_i^\dagger + \psi_i^\dagger\psi_i = 1$}.

These operators are collected into a row vector {$\Psi^\dagger=[\psi_1^\dagger,\dots,\psi_L^\dagger]$} and a column vector {$\Psi=[\psi_1,\dots,\psi_L]^T$}. An {$L\times L$} unitary matrix can act on them.

Our Hamiltonians look like {$\mathscr{H}=\Psi^\dagger\mathbf{H}\Psi=\sum_{1\leq i,j\leq L}H_{i,j}\psi_i^\dagger \psi_j$}. Here we may need to expand this to include the hole states and perhaps the vacuum state and the fully filled state. The fact that the Hamiltonian is Hermitian means that {$H_{j,i}=H_{i,j}^*$}.

A symmetry operation {$\mathscr{U}$} is defined on the Hilbert space, and in particular, on the single particle states so that {$|\langle i'|j'\rangle| = |\langle i|j\rangle| $} where {$|i'\rangle=\mathscr{U}|i\rangle, |j'\rangle=\mathscr{U}|j\rangle$}. A symmetry operation can be understood to act on the operator {$\Psi^\dagger$} whose {$L$} components construct the Hilbert space. The operator {$\mathbb{i}\mathscr{I}$} can be understood to act on these components by multiplying them by {$i$}. Then we can distinguish whether {$\mathscr{U}$} is linear {$\mathscr{U}(\mathbb{i}\mathscr{I})\mathscr{U}^{-1}=\mathbb{i}\mathscr{I}$} or antilinear {$\mathscr{U}(\mathbb{i}\mathscr{I})\mathscr{U}^{-1}=-\mathbb{i}\mathscr{I}$}.

Our symmetry operations have four kinds of constructions {$\breve{H}_{ij}=$}

• {$\sum_{1\leq i',j'\leq L}U_{ii'}H_{i'j'}U_{j'j}^\dagger$} usual linear
• {$\sum_{1\leq i',j'\leq L}U_{ii'}H_{i'j'}^*U_{j'j}^\dagger$} usual antilinear (time reversal)
• {$\sum_{1\leq i',j'\leq L}U_{ii'}^*H_{i'j'}U_{j'j}^T$} transposing linear (charge conjugation)
• {$\sum_{1\leq i',j'\leq L}U_{ii'}^*H_{i'j'}^*U_{j'j}^T$} transposing antilinear (sublattice)

For the transposing symmetry operations we furthermore want {$-\breve{\mathbf{H}}_{ij}^T$} yielding

• {$-\sum_{1\leq i',j'\leq L}U_{jj'}H_{j'i'}^*U_{i'i}^\dagger$} transposing linear (charge conjugation)
• {$-\sum_{1\leq i',j'\leq L}U_{jj'}H_{j'i'}U_{i'i}^\dagger$} transposing antilinear (sublattice)

Wigner's theorem

Wigner's theorem is the grounds for focusing on unitary and antiunitary transformations.

• Every unitary transformation {$U$} of a Hilbert space {$\mathcal{H}$} yields a Wigner symmetry {$\mathcal{U}$} on ray space, by conjugating density matrices: {$\mathcal{U}$}(p(|\psi\rangle))=U\rho(|\psi\rangle)U^{-1}$}. A density matrix describes an ensemble of physical systems as quantum states, allowing for the calculation of the probabilities of outcomes of measurements according to the Born rule.
• Wigner's theorem, conversely, states that given a Wigner symmetry on the ray space, it is possible to extend it in a natural way, via the vectors of unit length, to all of the Hilbert space as either a linear unitary operator or an antilinear antiunitary operator.

Proof of Wigner's theorem

• Tobias Osborne Assumes separability.
• R. Simon, N. Mukunda, S. Chaturvedi, V. Srinivasan. Two elementary proofs of the Wigner theorem on symmetry in quantum mechanics.
  • Note that the Bloch sphere, the ray space of a two-dimensional Hilbert space, is key to these proofs.
• Daniel D. Spiegel. A Simple Constructive Proof of Wigner's Theorem. Does not assume separability and allows the symmetry transformation to go between different Hilbert spaces.
• Sometimes viewed as a consequence of the Fundamental Theorem of Projective Geometry. See also homography.
• Norman Weinberger. The fundamental theorem of projective geometry.

Key to the proof

{$|\psi\rangle=\sum_j c_j|\psi_j\rangle, |\psi'\rangle=\sum_jc_j\psi_j'$}

{$|c_j|^2=|c_j'|^2$} because {$|\langle\psi_j|\psi\rangle|^2=|\langle u\psi_j|\overline{\psi}\rangle |^2$}

{$|c_j+c_1|^2=|c_j'+c_1'|^2$}

{$|1 + \frac{c_1}{c_j}|^2=|1+\frac{c_1'}{c_j'}|^2$}

{$c'_j=c_je^{i\theta_j},c_1'=c_1e^{i\theta_1}, \frac{c_1'}{c_j'}=\frac{c_1}{c_j}e^{i(\theta_1-\theta_j)}$} and let {$\beta=\theta_1-\theta_j$}

{$\frac{c_1}{c_j}=e^{i\alpha}$}

{$|1+e^{i\alpha}|^2=|1+e^{i(\alpha + \beta)}|^2$}

{$(1 +\cos\alpha)^2+\sin^2\alpha = (1+\cos (\alpha + \beta))^2+\sin^2(\alpha + \beta)$}

{$1+2\cos\alpha = 1+2\cos(\alpha+\beta)$}

{$\cos\alpha=\cos (\alpha + \beta)$} means {$\textrm{Re}\frac{c_1}{c_j}=\textrm{Re}\frac{c_1'}{c_j'}$} and implies {$\beta=0+2\pi$} unitary or {$\beta=-2\alpha + 2\pi$} antiunitary

{$\sin\alpha = -\sin(-\alpha)$} means {$\textrm{Im}\frac{c_1}{c_j}=\pm\textrm{Im}\frac{c_1'}{c_j'}$}

Usual and transposing symmetries

Another foundation is the notion of transposing symmetry, which takes particles to holes and vice versa. The holes may be anti-particles.

Usual symmetries fix the graded space {$\mathscr{U}_{USL}(\mathcal{V}_{N_p})=\mathcal{V}_{N_p}, \forall N_p$}

Usual symmetry acts on operators {$\mathscr{U}_{USL}\Psi^\dagger\mathscr{U}_{USL}^{-1}=\Psi^\dagger\mathbf{U}_{USL}$} where {$\mathbf{U}_{USL}$} is an {$L\times L$} unitary matrix that encodes the symmetry operation as {$\mathscr{U}_{USL}\psi_i^\dagger\mathscr{U}_{USL}^{-1}=\sum_{j=1}^L\psi_j^\dagger(U_{USL})_{ji}$}.

These are linear symmetries {$\mathscr{U}_{USL}(i\mathscr{I}\mathscr{U}_{USL}^{-1}=i\mathscr{I}$} where {$\mathscr{U}_{USL}\psi_i^\dagger\mathscr{U}_{USL}^{-1}=\sum_{j=1}^L\psi_j^\dagger(U_{USL})_{ji}$} and antilinear symmetries

Transposing symmetries

Four symmetries

Symmetries

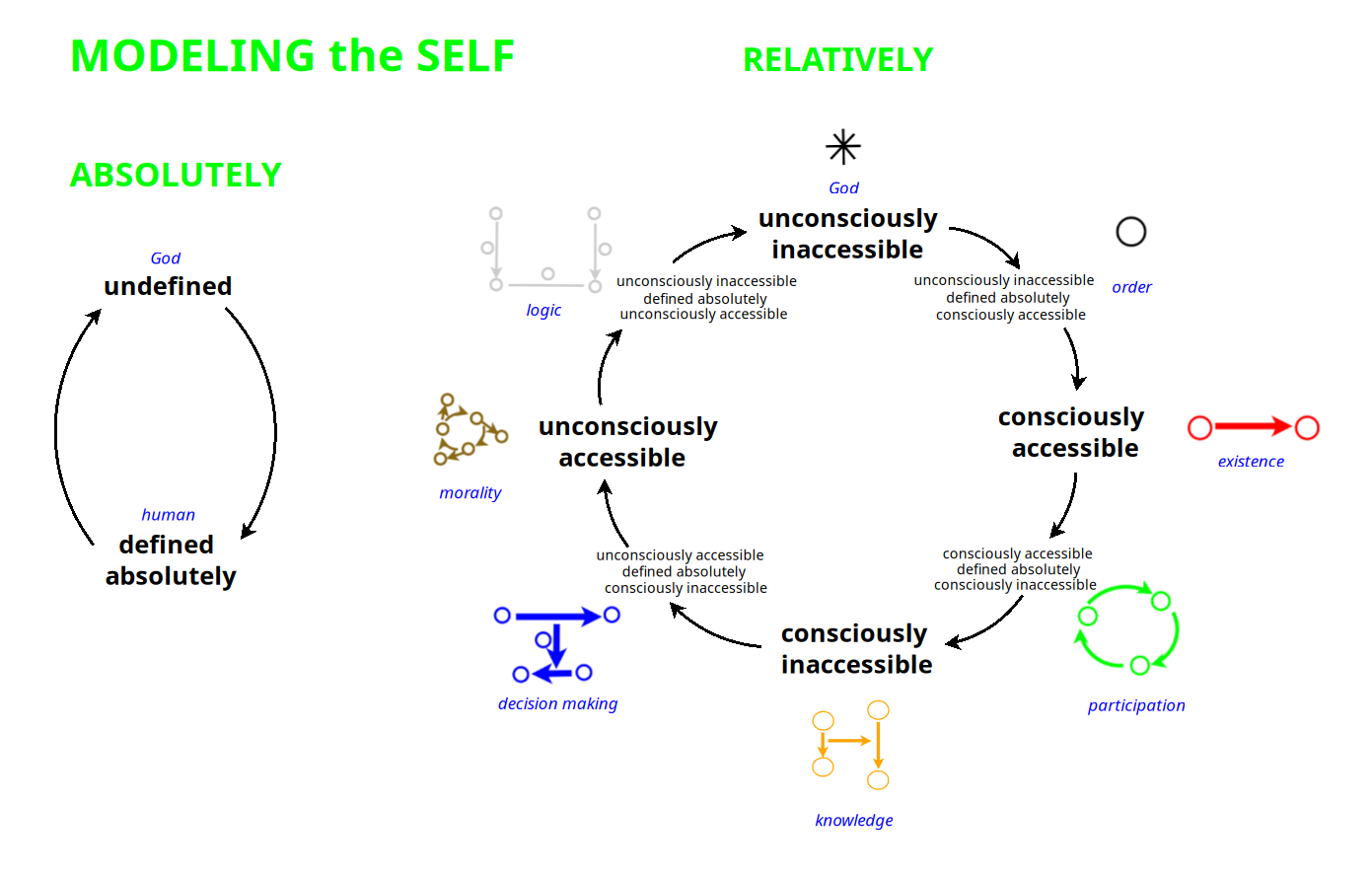
The symmetries are applicable to the Hamiltonian, which is the self. The self can be understood as undefined or defined absolutely, or also defined relatively, unconsciously or consciously accessible (imaginable), unconsciously or consciously inaccessible (unimaginable). If defined relatively, then it can also be defined absolutely, if both regard to accessibility and inaccessibility.

10 anti-unitary symmetries. Anti-unitary is complex conjugation times unitary.

Ludwig explains quantum symmetries in terms of first quantization (wave function) and second quantization (creation {$\hat{\psi}^\dagger_i$} and annihilation {$\hat{\psi}_i$} operators). For fermions, we have the anticommutating relations {$\hat{\psi}_i\hat{\psi}^\dagger_j = -\hat{\psi}^\dagger_j\hat{\psi}_i + \delta_{ij}$} and also {$\hat{\psi}_i\hat{\psi}_j = -\hat{\psi}_j\hat{\psi}_i, \hat{\psi}^\dagger_i\hat{\psi}^\dagger_j = -\hat{\psi}^\dagger_j\hat{\psi}^\dagger_i$}. Here the creation vector {$\hat{\psi}^\dagger=[\hat{\psi}^\dagger_1,\hat{\psi}^\dagger_2,\dots,\hat{\psi}^\dagger_n]$} is a row vector, and the annihilation vector {$\hat{\psi}=[\hat{\psi}_1,\hat{\psi}_2,\dots,\hat{\psi}_n]^T$} is a column vector.

The second quantized Hamiltonian is {$\hat{H}=\sum_{A,B}\hat{\psi}^\dagger_{A}H_{A,B}\hat{\psi}_B=\hat{\psi}^\dagger H\hat{\psi}$}

Here the labels {$A,B$} refer to the {$N$} states (or lattice sites which may be distinguished by extra information such as spin). The Hamiltonian {$H_{A,B}$} is a matrix of numbers, called the first quantization (or single-particle) Hamiltonian. We are interested in large {$N>>1$}, the thermodynamic limit.

Suppose that the Hamiltonian {$H_{A,B}$} is invariant under a group {$G_0$} of symmetries. There exist a representation of {$G$} in terms of {$N\times N$} unitary matrices {$U$}. Unitary means that {$U=U^\dagger$}. These matrices commute with the first quantized Hamiltonian. {$UH=HU$} means that {$UHU\dagger=H$}.

In terms of second quantization, this corresponds to operators {$\hat{U}$} acting on the Fermion Fock space as follows.

{$\hat{\mathcal{U}}\hat{\psi}_A\hat{\mathcal{U}}^{-1}=\sum_B U^\dagger_{A,B}\hat{\psi}_B$}	{$\hat{\mathcal{U}}\hat{\psi}^\dagger_A\hat{\mathcal{U}}^{-1}=\sum_B \hat{\psi}^\dagger_B U_{B,A}$}
the annihilation column vector {$\hat{\psi}$} is converted into a collection of annihilation column vectors with coefficients in the creation matrix {$U^\dagger$}	the creation row vector {$\hat{\psi}$} is converted into a collection of creation row vectors with coefficients in the annihilation matrix {$U={U^\dagger}^{-1}$}

The operators {$\hat{\mathcal{U}}$} and {$\hat{H}$} commute: {$\hat{\mathcal{U}}\hat{H}\hat{\mathcal{U}}^{-1}=\hat{H}$} Can I show this? Consider {$\hat{\mathcal{U}}\hat{H} = \hat{\mathcal{U}}\hat{\psi}^\dagger H\hat{\psi}$}

Three symmetries

Given the annihilation operator {$\Psi=[\psi_1, \dots, \psi_L]^T$} and creation operator {$\Psi^{\dagger}=[\psi_1^\dagger,\dots,\psi_L^\dagger]$}, we may apply a usual symmetry operator {$\mathit{U}_{USL}\Psi^\dagger\mathscr{U}_{USL}^{-1}=\Psi^\dagger\mathbf{U}_{USL}$} or a transposing symmetry operator {$\mathit{U}_{TRN}\Psi^\dagger\mathscr{U}_{TRN}^{-1}=\Psi\mathbf{U}_{USL}^*$}.

We get four kinds of operator (linear or antilinear vs. usual or transposing). We can show that the operators square to {$+1$} and possibly {$-1$} but note that the relationships for the related unitary matrices are more subtle because they depend on what happens when the matrix is moved outside of the conjugation by the symmetry operator.

• trivial operator
• time reversal operator {$\mathscr{T}$} is usual antilinear. {$\mathscr{T}^2=\pm 1=T, \mathbf{U}_T\mathbf{U}_T^*=T\mathbf{1}$}
• charge conjugation operator {$\mathscr{C}$} is transposing linear. {$\mathscr{C}^2=\pm 1=C, \mathbf{U}_C\mathbf{U}_C^*=C\mathbf{1}$}
• sublattice symmetry operator {$\mathscr{S}$} is transposing antilinear. {$\mathscr{S}^2= 1, \mathbf{U}_S\mathbf{U}_S=\mathbf{1} $}

Note that {$\mathscr{S}=\mathscr{T}\mathscr{C}$} and {$\mathscr{S}^2=\mathscr{I}$}. This means {$\mathscr{T}\mathscr{C}\mathscr{T}\mathscr{C}=\mathscr{I}$} and so {$\mathscr{I}=\mathscr{T}^2\mathscr{T}^{-1}\mathscr{C}\mathscr{T}\mathscr{C}^{-1}\mathscr{C}^2=T\mathscr{T}^{-1}\mathscr{C}\mathscr{T}\mathscr{C}^{-1}C$}. Then {$T^{-1}C^{-1}=\mathscr{T}^{-1}\mathscr{C}\mathscr{T}\mathscr{C}^{-1}=TC$} bęcause {$T,C\in\{-1,+1\}$}. Thus {$\mathscr{C}\mathscr{T}=\mathscr{T}\mathscr{C}TC$} and we can have {$T=C$} (if {$\mathscr{T}$} and {$\mathscr{C}$} commute) or {$T=-C$} (if they anticommute).

In squaring the operators, note that for charge conjugation, we have a transposing operation. If {$L$} is even, then we consider {$N_P=L/2-1$} to get {$e^{i2\theta}=1$}. Otherwise, if {$L$} is odd, then this operator must square to {$+1$}.

• linear {$\mathscr{S}H=-H\mathscr{S}$} sublattice, parity
• antilinear {$\mathscr{C}H\mathscr{C}^{-1}=-H, \mathscr{C}^2=\pm\mathbb{I}$} charge conjugation, particle-hole
• antilinear {$\mathscr{T}H\mathscr{T}^{-1}=H, \mathscr{T}^2=\pm\mathbb{I}$} time reversal
• {$CH^*C^{-1}=-H, C^*C=\pm\mathbb{I}$}
• {$TH^*T^{-1}=H, T^*T=\pm\mathbb{I}$}

Time reversal

Time reversal is a feature of the time-evolution operator {$\hat{\mathcal{U}}(t)=e^{itH}$} which relates the Lie algebra and the Lie group. We have {$\hat{\mathcal{T}}\hat{\mathcal{U}}(t)\hat{\mathcal{T}}^{ž1}=\hat{\mathcal{U}}(-t)$}.

{$T$} is (antilinear? anticommuting, ...?) so it must contain the final linear complex structure {$J_k$}, the one that anticommutes with the elements of {$\frak{m}_k$} whereas the previous {$J_1, \dots J_{k-1}$} commute.

Charge conjugation

{$C$} is based on {$J_2$} because...

The restrictions are based on {$J_1$} grouped with final pairs yielding {$J_1J_2J_3, J_1J_4J_5, J_1J_6J_7$} which one short of the anticommuting linear complex structure.

Math Stack Exchange. Andrius Kulikauskas. How is this antilinear map (charge conjugation) represented as a complex matrix?

Sublattice symmetry {$\mathbf{U}_S$}

The sublattice symmetry {$1_{p,q}H1_{p,q}=-H$}. The left hand side "conjugates" the matrix by setting its two off-diagonal matrices to negative, which is the same as converting the whole matrix to its negative. This means that the diagonal blocks are zero, which we see whenever we have all three symmetries. Whereas for a single symmetry we can have nonzero diagonal blocks, even in the case of {$H^*=-H$} because here the conjugation takes place algebraically.

The sublattice symmetry {$\mathbf{U}_S$} has eigenvalues restricted to {$\pm 1$} thus can be written at {$\mathbf{1}_{p,q}$}.

Applying the symmetry (by seeing what commutes with operator {$iJ_1$}) breaks up the space into two subspaces. And letting go of the symmetry (by seeing what commutes with a mutually anticommmuting operator {$iJ_2$}) has the subspaces be of the same size and contain the same information.

This relates to the symmetry of counting. There is a distinction between counting forwards and backwards and then the two directions have to be the same size. Similarly, we can think in terms of creation and annihilation operators.

In the real case, with each new operator {$J_i$}, the sublattice symmetry is either arising or disappearing. And when it arises, it is bringing together time reversal {$\mathbf{U}_T$} and charge conjugation {$\mathbf{U}_C$} in one of four ways that the periodicity cycles through.

The sublattice symmetry {$S$}

• there may be no symmetries
• there may only be the sublattice symmetry and {$S^2=+1$}
• {$S$} may not exist but either {$C$} or {$T$} does
• the sublattice symmetry is one of three symmetries and {$S^2=+1 = T^2C^2$}
  • {$T^2=+1, C^2=+1$}
  • {$T^2=-1, C^2=-1$}
• the sublattice symmetry is one of three symmetries and {$S^2=-1 = T^2C^2$}
  • {$T^2=+1, C^2=-1$}
  • {$T^2=-1, C^2=+1$}

The sublattice symmetry is important when there is a double symmetry, involving both {$C$} and {$T$}, thus a triple symmetry.

Note that {$\mathbf{U}_T\mathbf{U}_T^*=\mathbf{1}$}, {$\mathbf{U}_C\mathbf{U}_C^*=\mathbf{1}$}, whereas {$\mathbf{U}_S\mathbf{U}_S=\mathbf{1}$}.

We have {$\mathbf{U}_S=\mathbf{U}_T\mathbf{U}_C^*$} but also, taking inverses, and using the equations above to calculate those inverses, we have {$\mathbf{U}_S=\mathbf{U}_C\mathbf{U}_T^*$}.

Conjugation

There are two kinds of conjugation. Algebraically, {$H^*$} indicates an change in the disposition of the self, who we identify with, as regards (the self as being) stepping in or (the self as context) stepping out. But the Hamiltonian is a Hermitian matrix so this is the same as taking the transpose. Taking the transpose changes the relationship with the context, whether the self acts on the context or the context acts on the self. Whereas the operation {$1_{p,q}H1_{p,q}$} switches the off-diagonal to negative. This changes our internal self-organization in terms of the relationship between particles and holes, which is known and unknown, switching that.

Conjugate transpose of {$M$} means that the action of {$M$} on one side (to the right) is now understood on the other side (to the left). And since we are dealing with complex matrices, typically unitary matrices, the conjugation is what algebraically balances this switching of sides. For the conjugate is what balances a complex number so that it can have a norm, as with {$cc*=c*c=|c|$}. The conjugate transpose replace yourself acting upon another with another acting likewise upon you. In the Hermitian case, they are both the same.

Sublattice symmetry

{$\mathbf{U}_S=\mathbf{1}_{p,q}$}

Sublattice symmetry is transposing antilinear. It maps particles to holes and vice versa. In the q-dimensional sublattice, in the human subspace, it maps particles to negative holes, where negative indicates the conscious, thus the unknown.

The sublattice symmetry establishes an absolute frame by which the self is absolutely defined. It distinguishes between the undefined, given by eigenvalues {$+1$}, and the the defined, given by eigenvalues {$-1$}. The defined distinguishes the defined undefined {$+1$} and the defined defined {$-1$}, mapping the one to the other, in what is defined. Regarding what is undefined, it maps the defined undefined to the defined undefined, and similarly with the defined defined. When we go from the absolutely defined back to the undefined, then the dimensions, {$p$} for the undefined and {$q$} for the defined, have to match.

This absolute frame establishes the meaning of the real and purely imaginary numbers within the complex numbers. The real numbers describe what is undefined, and the purely imaginary numbers describe what is defined, distinguishing the defined undefined and the defined defined.

Sublattice symmetry is transposing antilinear.

Consider change of basis {$\tilde{\Psi}^\dagger=\Psi^\dagger \mathbf{R}$} where {$\mathbf{R}$} is unitary, {$\mathbf{R}\mathbf{R}^\dagger = 1$}

Given {$\mathscr{S}\Psi^\dagger\mathscr{S}^{-1}=\Psi^T\mathbf{U}_S^*$} and {$\mathscr{S}\tilde{\Psi}^\dagger\mathscr{S}^{-1}=\tilde{\Psi}^T\tilde{\mathbf{U}}_S^*$}

{$\mathscr{S}(\Psi^\dagger\mathbf{R})\mathscr{S}^{-1}=(\Psi^T\mathbf{R}^*)\tilde{\mathbf{U}}_S^*$} by substitution of {$\tilde{\Psi}^T=\Psi^TR^*$}

{$\mathscr{S}\Psi^\dagger\mathscr{S}^{-1}\mathbf{R}^*=\Psi^T\mathbf{R}^*\tilde{\mathbf{U}}_S^*$} by antilinearity

{$\Psi^T\mathbf{U}_S^* = \Psi^T\mathbf{R}^*\tilde{\mathbf{U}}_S^*\mathbf{R}^T$}

{$\mathbf{U}_S^* = \mathbf{R}^*\tilde{\mathbf{U}}_S^*\mathbf{R}^T$}

{$\mathbf{U}_S=\mathbf{R}\tilde{\mathbf{U}}_S\mathbf{R}^\dagger$}

Time reversal

Time reversal is usual antilinear.

Consider change of basis {$\tilde{\Psi}^\dagger=\Psi^\dagger \mathbf{R}$} where {$\mathbf{R}$} is unitary, {$\mathbf{R}\mathbf{R}^\dagger = 1$}

Given {$\mathscr{T}\Psi^\dagger\mathscr{T}^{-1}=\Psi^\dagger\mathbf{U}_T$} and {$\mathscr{T}\tilde{\Psi}^\dagger\mathscr{T}^{-1}=\tilde{\Psi}^\dagger\tilde{\mathbf{U}}_T$}

{$\mathscr{T}(\Psi^\dagger\mathbf{R})\mathscr{T}^{-1}=(\Psi^\dagger\mathbf{R})\tilde{\mathbf{U}}_T$} by substitution

{$\mathscr{T}\Psi^\dagger\mathscr{T}^{-1}\mathbf{R}^*=\Psi^\dagger\mathbf{R}\tilde{\mathbf{U}}_T$} by antilinearity

{$\mathscr{T}\Psi^\dagger\mathscr{T}^{-1}$}{$ =\Psi^\dagger\mathbf{R}\tilde{\mathbf{U}}_T{\mathbf{R}^{-1}}^*$}{$= \Psi^\dagger\mathbf{R}\tilde{\mathbf{U}}_T{\mathbf{R}^\dagger}^*$}{$=\Psi^\dagger\mathbf{R}\tilde{\mathbf{U}}_T\mathbf{R}^T$}

{$\Psi^\dagger\mathbf{U}_T=\Psi^\dagger\mathbf{R}\tilde{\mathbf{U}}_T\mathbf{R}^T$}

{$\mathbf{U}_T=\mathbf{R}\tilde{\mathbf{U}}_T\mathbf{R}^T$}

Charge conjugation

Charge conjugation is transposing linear.

Consider change of basis {$\tilde{\Psi}^\dagger=\Psi^\dagger \mathbf{R}$} where {$\mathbf{R}$} is unitary, {$\mathbf{R}\mathbf{R}^\dagger = 1$}

Given {$\mathscr{C}\Psi^\dagger\mathscr{C}^{-1}=\Psi^T\mathbf{U}_C^*$} and {$\mathscr{C}\tilde{\Psi}^\dagger\mathscr{C}^{-1}=\tilde{\Psi}^T\tilde{\mathbf{U}}_C^*$}

{$\mathscr{C}(\Psi^\dagger\mathbf{R})\mathscr{C}^{-1}=(\Psi^T\mathbf{R}^*)\tilde{\mathbf{U}}_C^*$} by substitution of {$\tilde{\Psi}^T=\Psi^TR^*$}

{$\mathscr{C}\Psi^\dagger\mathscr{C}^{-1}\mathbf{R}=\psi^T\mathbf{R}^*\tilde{\mathbf{U}}_C^*$} by linearity and by tranposition

{$\mathscr{C}\Psi^\dagger\mathscr{C}^{-1}=\Psi^T\mathbf{R}^*\tilde{\mathbf{U}}_C^*\mathbf{R}^{-1}$}

{$\Psi^T\mathbf{U}_C^*=\Psi^T\mathbf{R}^*\tilde{\mathbf{U}}_C^*\mathbf{R}^\dagger$}

{$\mathbf{U}_C^*=\mathbf{R}^*\tilde{\mathbf{U}}_C^*\mathbf{R}^\dagger$}

{$\mathbf{U}_C=\mathbf{R}\tilde{\mathbf{U}}_C\mathbf{R}^T$}

Complex Bott periodicity is based on {$H$} and describes God as the reference for an absolute frame. God is frameless. He takes on an absolute frame. An absolute frame of an absolute frame is framelessness. Framelessness is without a basis, and the absolute frame provides an absolute basis.

Real Bott periodicity is based on {$H^*$} and describes human as the reference for a relative frame. Charge conjugation is the symmetry of the inaccessible, the unimaginable, as when the Hamiltonian is purely imaginary. Time reversal is the symmetry of the accessible, the imaginable, as when the Hamiltonian is purely real. These can be either unconscious (squaring to {$+1$}) or conscious (squaring to {$-1$}). The basis is chosen relative to the symmetry, when it is alone, and relative to the absolute frame, when there are all three symmetries, which opens up a complementary symmetry. The absolute frame allows us to switch from the imaginable to the unimaginable or vice versa. Alternating, back and forth, yields the divisions of everything.

For accessibility, imaginability, the reference point is the unitary group, just as with God. For inaccessibility, unimaginability, the reference points are, unconsciously, the orthogonal group, and consciously, the symplectic group.

nullsome	unconsciously unimaginable
onesome	unconsciously unimaginable -> consciously imaginable	inverts both
twosome	consciously imaginable
threesome	consciously imaginable -> consciously unimaginable	stays conscious
foursome	consciously unimaginable
fivesome	consciously unimaginable -> unconsciously imaginable	inverts both
sixsome	unconsciously imaginable
sevensome	unconsciously imaginable -> unconsciously unimaginable	stays unconscious
eightsome	unconsciously unimaginable

This describes the relationship between having no subsystem (God) and having a subsystem (human, as opposed to God).

The Hamiltonians express what is left free by the symmetries. They are the freedom of the self. They express how the freedom expresses the constraints. The freedom is channeled in perspectives.

Twofold periodicity is driven by the symmetry {$SHS^{-1}=-H$} which acts on {$H$} directly, thus bringing out the symmetry of the Hermitian matrix, yielding a unitary matrix upon exponentiation {$e^{iH}$}.

God

There is no additional symmetry but there is simply the fact that {$H=H^\dagger$} is Hermitian.

Human

Here we are working with {$U(2r)$} and we allow for complex numbers. We have operators {$K_j=iJ_j$} with {$K_j^2=\mathbb{I}$} splitting the complex vector space {$\mathbb{C}^{2r}$} into two components with eigenvalues {$+1$} and {$-1$} which can be of different size. In particular, {$J_1$} can be a diagonal matrix with {$p$} entries {$i$} and {$q$} entries {$-i$}. Then {$U(p)\times U(q)$} is the subset of {$U(p+q)$} which commutes with {$J_1$}. These are matrices with blocks {$u_1$} and {$u_2$} on the diagonal. The matrices that anticommute with {$J_1$} have blocks on the off-diagonal and they express {$\frak{u}$}{$(2r)\backslash\frak{u}$}{$(r)\oplus\frak{u}$}{$(r)$}.

We usually write {$J_1=\begin{pmatrix} & -1 \\ 1 & \\ \end{pmatrix}$} but this would force the eigenspaces of {$iJ_1$} to be of equal size. Instead, since we are working with a complex vector space, we can write:

{$J_1=\begin{pmatrix} i & \\ & -i \\ \end{pmatrix}, J_2=\begin{pmatrix} & i \\ i & \\ \end{pmatrix}$}

For {$J_1$}, the number of {$i$} and the number of {$-i$} on the diagonal can be different, {$p$] and {$q$}, respectively, with consequences for {$iJ_1$}. In order to define {$J_2$}, we need {$p=q$}. {$J_2$} is an isometry of {$V_+$} and {$V_-$} and it squares to {$-1$}. {$J_1$} and {$J_2$} anticommute. Consider

{$\begin{pmatrix} u_1 & \\ & u_2 \\ \end{pmatrix}\begin{pmatrix} & i \\ i & \\ \end{pmatrix}=\begin{pmatrix} & iu_1 \\ iu_2 & \\ \end{pmatrix}, \begin{pmatrix} & i \\ i & \\ \end{pmatrix}\begin{pmatrix} u_1 & \\ & u_2 \\ \end{pmatrix}=\begin{pmatrix} & iu_2 \\ iu_1 & \\ \end{pmatrix}$}

Commutation implies that {$u_1=u_2$} and so we are left with {$U(n)$}. Anticommutation implies {$u_1=-u_2$}. In either case, the resulting matrices are isomorphic to {$U(n)$}

{$\begin{pmatrix} u & \\ & u \\ \end{pmatrix}, \; \begin{pmatrix} u & \\ & -u \\ \end{pmatrix}$}

In terms of the corresponding Lie algebras, this simply means that we are decomposing {$\frak{u}$}{$(n)\oplus\frak{u}$}{$(n)$}.

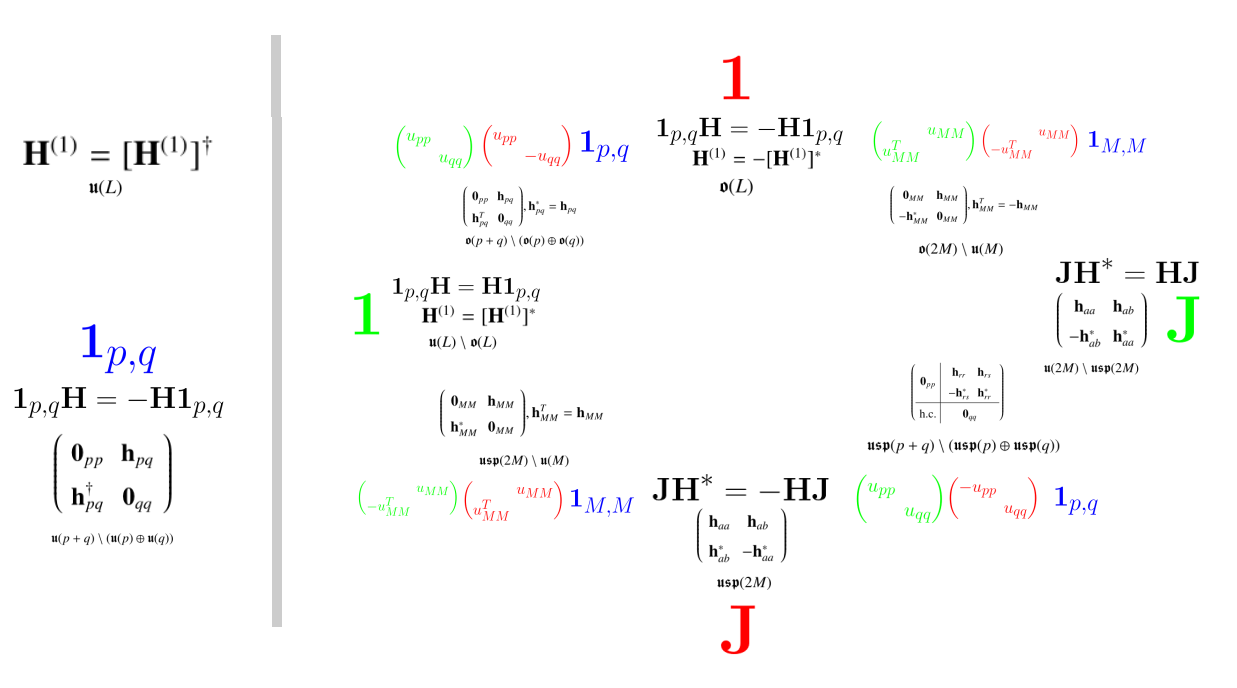
There is the symmetry {$1_{p,q}H1_{p,q}=-H$} where {$S=1_{p,q}$}.

{$H=-1_{p,q}H1_{p,q}=-\begin{pmatrix} 1_p & \\ & -1_q \\ \end{pmatrix}\begin{pmatrix} h_{aa} & h_{ab} \\ h_{ba} & h_{bb} \\ \end{pmatrix}\begin{pmatrix} 1_p & \\ & -1_q \\ \end{pmatrix} $}

{$=-\begin{pmatrix} h_{aa} & h_{ab} \\ -h_{ba} & -h_{bb} \\ \end{pmatrix}\begin{pmatrix} 1_p & \\ & -1_q \\ \end{pmatrix} $}

{$=-\begin{pmatrix} h_{aa} & -h_{ab} \\ -h_{ba} & h_{bb} \\ \end{pmatrix}$}

{$=\begin{pmatrix} -h_{aa} & h_{ab} \\ h_{ba} & -h_{bb} \\ \end{pmatrix}$}

{$h_{aa}=0, h_{bb}=0$}. Also, {$H$} is Hermitian implies {$h_{ba}=h_{ab}^\dagger$}

{$H=\begin{pmatrix} & h_{ab} \\ h_{ab}^\dagger & \\ \end{pmatrix}$}

Note that we are missing hermitian matrices of the form {$M=\begin{pmatrix} h_{aa} & \\ & h_{bb} \\ \end{pmatrix}$}, where {$iM$} generate the Lie algebra {$\frak{u}(\textrm{p})\oplus\frak{u}(\textrm{q})$}. Thus {$i\mathcal{H}$} is given by {$\frak{u}(\textrm{p+q})\backslash\frak{u}(\textrm{p})\oplus\frak{u}(\textrm{q})$}.

Note that we may have {$p\neq q$} and so this is not the same as complex conjugation.

In continuing, we are identifying {$h_pq=h_pq^\dagger$}, which we already knew. All that we are truly doing is insisting that {$q=p$}. Whereas all that we did to get here was to impose a symmetry that distinguished between {$V_+$} and {$V_-$}, thus {$p$} and {$q$} accordingly.

It seems that at any point we can adjust the overall dimension to be what we want it to be, at our convenience. This is similar to choosing the degree of precision, coarse or fine, and it doesn't affect our internal reality, which is given by our perspectives {$J_k$}, the structure of our Hamiltonian, its symmetries, and any related isometries.

God and human are distinguished upon distinguishing divine {$V_+$} and human {$V_-$}, where humans can swap back and forth between knowing and not knowing, upon reflection. What then matters is their relationship as given by the off-diagonal matrices. Then human and God are reunited upon matching their dimensions, in which case the distinction and the relationship disappear.

In going between the two states, note that there is a significant difference between {$\frak{u}$}{$(n)$} and {$\frak{u}$}{$(p)\oplus\frak{u}$}{$(q)$}. The quotient {$U(2n)/U(p)\times U(q)$} is the complex Grassmannian. Whereas qualitatively not much difference in the respective Hamiltonians, the complement {$\frak{m}_0$} and {$\frak{m}_1$}, as they are basically the same, just different dimension. Importantly, from the Hamiltonian point of view, the key difference is in the complement, and also in the constraints on the number - are there two eigenspaces - and are they forced to be equal in size?

Complex Bott periodicity models how we humans can be free of ourselves, frameless, by living through God.

Here there is always assumed to be a subsystem. We go back and forth between having two symmetries or just one.

{$T:H^*\rightarrow H$} sends {$a-bi$} to {$a+bi$} swapping imaginaries. {$C:H^*\rightarrow -H$} sends {$a-bi$} to {$-a-bi$} swapping reals.

Eightfold periodicity is driven by the conjugate {$H*$}, through two symmetries {$TH^*T^{-1}=H$} and {$CH^*C^{-1}=-H$}. Note that {$T$} is an ordinary symmetry, with no concept of holes or particles, whereas {$C$} is a transposing symmetry, with a concept of particles and holes. We walk through the Bott clock alternating between having both symmetries or having just one of them. Note that we start and end at {$C$}.

Consider what it means to have unmarked-marked opposites {$H$} and {$-H$} and twin unmarked-unmarked opposites, imaginary numbers {$i$} and {$j$} with {$\bar{i}=j$} and {$\bar{j}=i$}. Note that known (raw, direct, unreflected experience) and unknown (indirect, reflected) are unmarked and marked.

Note that {$H$} and {$H^\dagger$} are twin opposites. One is the context of the other. But neither is intrinsically primary, as regards the underlying norm. However, one is then chosen as the inhabited one, the resident one, the being. Note also, however, that the dual vector space has a notion of functional which is secondary and brings in a map into the field, which is a marker, making the dual vector space marked.

Note also that {$+1$} and {$-1$} are unmarked and marked only as the secondary operation (multiplication in a ring). In an additive group, such as {$\mathbb{Z}$} they are the same, they both serve as generators, because the identity is zero. Note also the difference between zero and a blank space, as opposites, here marked and unmarked.

The Hamiltonian describes the limits on what we can imagine, what we can access. Real describes what is accessible to us, and imaginary what is unaccessible, beyond what we can imagine. We start with the Hamiltonian being entirely imaginary, establishing the nullsome. With the sixsome, everything is real, giving the extent of our imagination. So I should look for a process by which the Hamiltonian becomes more accessible, more real. Charge conjugation describes what is unaccessible, imaginary, and time reversal describes what is accessible, real.

What drives the Bott clock is that the bases underling the symmetries are changing. When there is a single symmetry, then it can be expressed straightforwardly as 1 or J. But when there are two symmetries, then their bases need to be written in terms of the basis for the sublattice symmetry. I need to understand how the bases change as we go around the clock, alternating between the sublattice symmetry and the individual symmetries.

Going from a single symmetry to a double symmetry, the single symmetry gets embedded in an absolute context, changing its basis as necessary or not. This includes a new, complementary symmetry. Then that symmetry is considered in isolation, simplifying its basis relative to itself, then as such getting embedded in the absolute context. It is interesting that this yields new results, not going backwards.

Real Bott periodicity, assuming {$H^*$}, thus real numbers - imaginability, models how humans are trapped in ourselves.

Nullsome

{$C=\phi\otimes\mathbb{I}$}

{$\mathbf{H=-H^*}$}

{$\frak{o}\textrm{(L)}$}

The symmetry {$\mathbf{1_{p,q}H=-H1_{p,q}}$} can be written {$1_{p,q}H1_{p,q}= H^* = -H$}.

Onesome

{$C=\phi, T=\phi\otimes J_1$}

{$\begin{pmatrix} & h_{mm} \\ -h_{mm}^* & \end{pmatrix}$}

{$\frak{o}\textrm{(2L)} \backslash \frak{u}\textrm{(L)}$}

{$H$} and {$-H^*$} are separated, identified with going back and forth between subspaces, and real numbers are now allowed.

Twosome

{$T=J_2$}

{$\begin{pmatrix} h_{aa} & h_{ab} \\ -h_{ab}^* & h_{aa}^* \end{pmatrix}$}

{$\frak{u}\textrm{(2L)} \backslash \frak{sp}\textrm{(L)}$}

{$\mathbf{\begin{pmatrix} & 1_{mm} \\ -1_{mm} & \end{pmatrix}H^*=H\begin{pmatrix} & 1_{mm} \\ -1_{mm} & \end{pmatrix}}$}

The symmetry can be written

{$\begin{pmatrix} & -1_{mm} \\ 1_{mm} & \end{pmatrix}\mathbf{H}\begin{pmatrix} & 1_{mm} \\ -1_{mm} & \end{pmatrix}= \mathbf{H}^*$}

{$\begin{pmatrix} & -1_{mm} \\ 1_{mm} & \end{pmatrix}\begin{pmatrix} h_{aa} & h_{ab} \\ h_{ba} & h_{bb} \end{pmatrix}\begin{pmatrix} & 1_{mm} \\ -1_{mm} & \end{pmatrix}= \begin{pmatrix} h_{aa}^* & h_{ab}^* \\ h_{ba}^* & h_{bb}^* \end{pmatrix}$}

{$=\begin{pmatrix} -h_{ba} & -h_{bb} \\ h_{aa} & h_{ab} \end{pmatrix}\begin{pmatrix} & 1_{mm} \\ -1_{mm} & \end{pmatrix}= \begin{pmatrix} h_{bb} & -h_{ba} \\ -h_{ab} & h_{aa} \end{pmatrix} = \begin{pmatrix} h_{aa}^* & h_{ab}^* \\ h_{ba}^* & h_{bb}^* \end{pmatrix}$}

Thus {$h_{bb}=h_{aa}^*, h_{ba}=-h_{ab}^*$}.

Consequently, {$H=\begin{pmatrix} h_{aa} & h_{ab} \\ -h_{ab}^* & h_{aa}^* \end{pmatrix}$}

The absolute space and relative space are distinguished and allowed to have self-relations.

Threesome

{$C=J_2, T=J_3$}

{$\begin{pmatrix} & & h_{aa} & h_{ab} \\ & & -h_{ab}^* & h_{aa}^* \\ h_{aa}^\dagger & -h_{ab}^T & & \\ h_{ab}^\dagger & h_{aa}^T & & \end{pmatrix}$}

{$\frak{sp}\textrm{(2L)} \backslash \frak{sp}\textrm{(L)}\oplus\frak{sp}\textrm{(L)}$}

{$H$} and {$H^\dagger$} are separated.

Foursome

{$C=J_2$}

{$\begin{pmatrix} h_{aa} & h_{ab} \\ h_{ab}^* & -h_{aa}^* \end{pmatrix}$}

{$\frak{sp}\textrm{(L)}$}

{$\mathbf{\begin{pmatrix} & 1_{mm} \\ -1_{mm} & \end{pmatrix}H^*=-H\begin{pmatrix} & 1_{mm} \\ -1_{mm} & \end{pmatrix}}$}

The symmetry can be written

{$\begin{pmatrix} & -1_{mm} \\ 1_{mm} & \end{pmatrix}\mathbf{H}\begin{pmatrix} & 1_{mm} \\ -1_{mm} & \end{pmatrix}= -\mathbf{H}^*$}

{$\begin{pmatrix} & -1_{mm} \\ 1_{mm} & \end{pmatrix}\begin{pmatrix} h_{aa} & h_{ab} \\ h_{ba} & h_{bb} \end{pmatrix}\begin{pmatrix} & 1_{mm} \\ -1_{mm} & \end{pmatrix}= \begin{pmatrix} -h_{aa}^* & -h_{ab}^* \\ -h_{ba}^* & -h_{bb}^* \end{pmatrix}$}

{$=\begin{pmatrix} -h_{ba} & -h_{bb} \\ h_{aa} & h_{ab} \end{pmatrix}\begin{pmatrix} & 1_{mm} \\ -1_{mm} & \end{pmatrix}= \begin{pmatrix} h_{bb} & -h_{ba} \\ -h_{ab} & h_{aa} \end{pmatrix} = \begin{pmatrix} -h_{aa}^* & -h_{ab}^* \\ -h_{ba}^* & -h_{bb}^* \end{pmatrix}$}

Thus {$h_{bb}=-h_{aa}^*, h_{ba}=h_{ab}^*$}.

Consequently, {$H=\begin{pmatrix} h_{aa} & h_{ab} \\ h_{ab}^* & -h_{aa}^* \end{pmatrix}$}

The complementary space is allowed and united, allowing for diagonal elements. The negative sign of the bottom row has been swapped.

Fivesome

{$C=J_2, T=J_2J_4J_5$}

{$\begin{pmatrix} & h_{mm} \\ h_{mm}^* & \end{pmatrix}$}

{$\frak{sp}\textrm{(L)} \backslash \frak{u}\textrm{(L)}$}

The diagonal elements are made zero.

Sixsome

{$T=J_2J_4J_6$}

{$\mathbf{H=H^*}$}

{$\frak{u}\textrm{(L)} \backslash \frak{o}\textrm{(L)}$}

{$\mathbf{1_{p,q}H=H1_{p,q}}$}

The symmetry {$\mathbf{1_{p,q}H=H1_{p,q}}$} can be written {$1_{p,q}H1_{p,q}= H^* = H$}.

The off-diagonal blocks {$h_{mm}$} and {$h_{mm}^*$} are identified and united, making them real.

Sevensome

{$C=J_2J_4J_6=\phi, T=J_1J_6J_7$}

{$\begin{pmatrix} & h_{pq} \\ h_{pq}^* & \end{pmatrix}$}

{$\frak{o}\textrm{(2L)} \backslash \frak{o}\textrm{(L)}\oplus\frak{o}\textrm{(L)}$}

{$H$} and {$H^*$} are distinguished, and allowed to be non-square.

Eightsome

{$C=J_2J_4J_6=\phi$}

{$\mathbf{H=-H^*}$}

{$\frak{o}\textrm{(L)}$}

{$\mathbf{1_{p,q}H=-H1_{p,q}}$}

{$h_{pq}$} and {$h_{pg}^*$} are identified as negatives of each other. The negative sign of the bottom row has been swapped (from the zero onto {$h_{pq}^*$}).