• View
• Edit
• History
• Print

Outgrowths

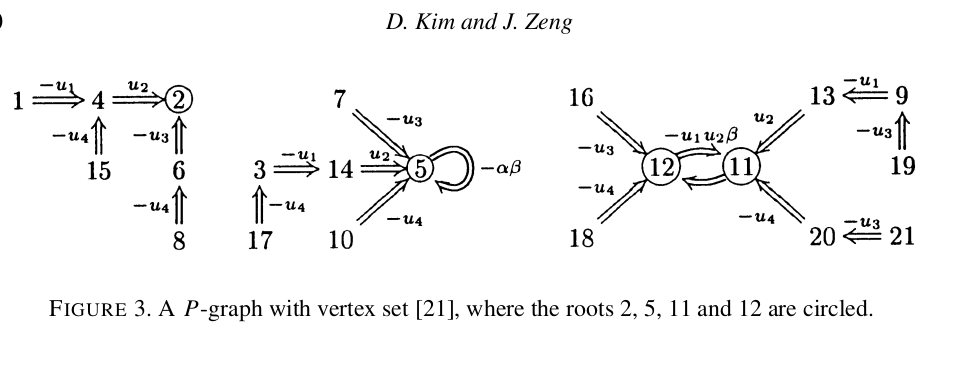
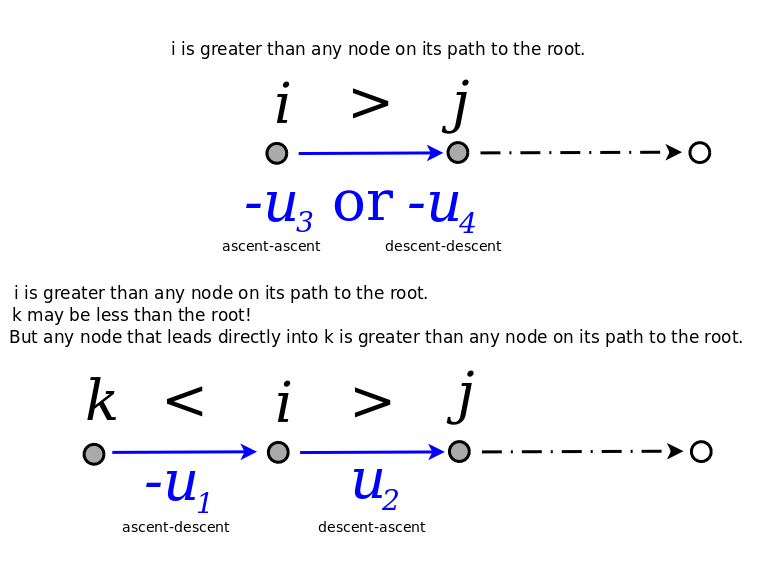
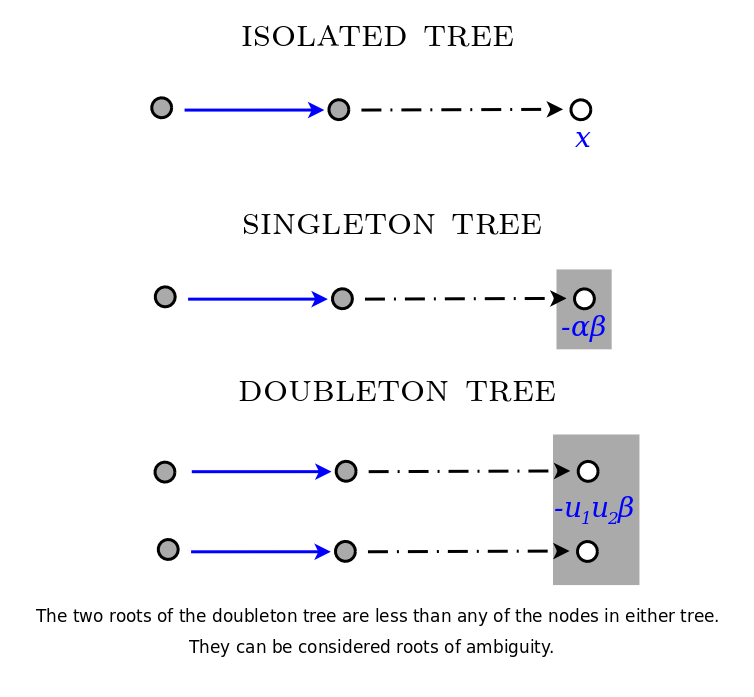
Kim-Zeng Trees

Combinatorial Interpretation of Orthogonal Sheffer Polynomial Coefficients

I am interpreting the combinatorial objects described in Dongsu Kim, Jiang Zeng. A Combinatorial Formula for the Linearization Coefficients of General Sheffer Polynomials.

Kim and Zeng write the recurrence relation as follows

• Kim and Zeng: {$P_{n+1}(x)=[x-(\alpha\beta + nu_3+nu_4)]P_n(x)- u_1u_2 n(n-1 +\beta )P_{n-1}(x)$}
• Kim and Zeng: {$P_{n+1}(x)=[x - (u_3+u_4)n + \alpha\beta)]P_n(x)-[u_1u_2n(n-1) + u_1u_2\beta n]P_{n-1}(x)$}

And here it is in my notation

• Andrius: {$P_{n+1}(x)=[x-(ln+cf)]P_n(x)-[kn(n-1) + nc]P_{n-1}(x)$}
• Andrius: {$P_{n+1}(x)=[x-(((-\alpha)+(-\beta))n+cf)]P_n(x)-(-\alpha)(-\beta)[n(n-1) + nc]P_{n-1}(x)$}