- MathNotebook
- MathConcepts
- StudyMath
- Geometry
- Logic
- Bott periodicity
- CategoryTheory
- FieldWithOneElement
- MathDiscovery
- Math Connections
Epistemology
- m a t h 4 w i s d o m - g m a i l
- +370 607 27 665
- My work is in the Public Domain for all to share freely.
- 读物 书 影片 维基百科
Introduction E9F5FC
Questions FFFFC0
Software
Math notebook, Logic, Statistics, Duality, Type theory
Investigation: Think through the conceptual significance of the Curry-Howard-Lambek correspondence and incorporate statistics
Understand the basis for the trinity
- How does the Goedel trinity (consistent, complete, creative) relate to the Curry-Howard-Lambek correspondence?
- What are the Curry-Howard-Lambek (unconditionality, nonsubjectivity, undeniability) analogues of contradiction: the set of all sets, the self-implicating modus ponens, the... How are contradiction and noncontradiction compatible? Consider the sevensome and the eightsome.
- Category theory is syntactic with set theory semantic; Logic is syntactic with category theory semantic; Is type theory syntactic where logic is semantic?
Understand in terms of set theory
- Understand various category theory concepts in terms of the category of sets.
- Consider how the correspondence of set theory and classical logic corresponds to category theory.
Understand how the concepts (connectives, quantifiers) are ingredients that build up a self-standing system
- Why do we have and use the logical connectives that we do?
- Are there eight connectives and do they express the divisions of everything? in a cumulative way?
- Is there a fivesome of logical connectives: {$\land$}, {$\lor$}, {$\exists x$},{$\forall x$} with the fifth being {$\neg$} (or implication)?
- Relate concepts from type theory, computation and programming.
- Understand the various limit and colimit constructs in terms of the category of sets, and how that relates to logic, Curry-Howard-Lambek and automata theory.
- Interpret Nand and Nor in terms of Curry-Howard-Lambek
- Interpret the Yoneda lemma in terms of Curry-Howard-Lambek
Develop my understanding of related concepts in the related subjects
- Type theory - amounts and units, proofs as terms, propositions as types
- Category theory - Limits vs colimits
- Statistics - nondeterminism, Markov kernels
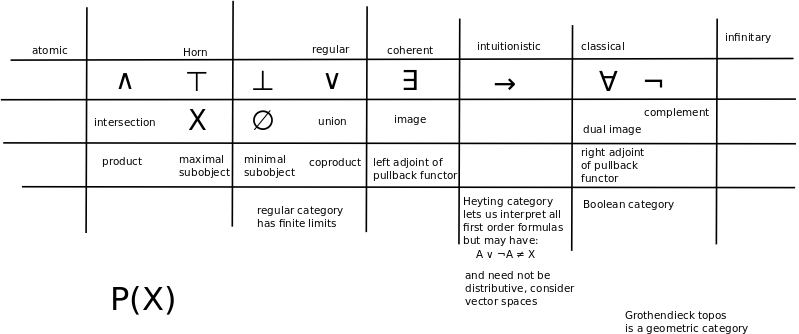
- Check my diagram as to the meaning of regular logic and coherent logic.
Goedel trinity
Robert Harper: Holy trinity:
- Logic: Proof theory
- Algebra: Algebraic structure: Categorical theory
- Programming: Computation: Type theory
Grounds a proper scientific discovery, a significant, permanent contribution.
Computational trinitarianism takes as equivalent a proof of a proposition, a program with output of some type, and a generalized element of some object.
- Proofs can be run.
- A proof is a program, and the formula it proves is the type for the program.
- Proofs can be represented as programs, and especially as lambda terms.
- The return type of a function (i.e., the type of values returned by a function) is analogous to a logical theorem, subject to hypotheses corresponding to the types of the argument values passed to the function. The program to compute that function is analogous to a proof of that theorem.
Running a program is, subjectively, analogous to human experience, as with the three kinds of dynamic language. Running a program expresses dynamics.
- Given a predicate with variables {$A(x_1,x_2,...,x_n)$} the symbols {$x_1,x_2,...,x_n$} may be interepreted in the following ways: as instances, as variables, and as abstracts (instances of variables). This is reminiscent of the three-cycle and of the trinity of type theory, proof theory and category theory.
Boolean algebra - divine knowledge. Heyting algebra (modeling decidability) - human knowledge.
Heyting algebra relates external implication ≤ and internal implication → as follows: (c ∧ a) ≤ b is equivalent to c ≤ (a → b). Note that this expression divides c and a, making one an external condition and another an internal condition. Thus it defines subsystems of internal logic.
- Every Boolean algebra is a Heyting algebra when a → b is defined as usual as ¬a ∨ b.
- It follows from the definition that 1 ≤ 0 → a, corresponding to the intuition that any proposition a is implied by a contradiction 0.
- Although the negation operation ¬a is not part of the definition, it is definable as a → 0.
- The intuitive content of ¬a is the proposition that to assume a would lead to a contradiction.
- The definition implies that a ∧ ¬a = 0.
- It can further be shown that a ≤ ¬¬a.
- The converse, ¬¬a ≤ a, is not true in general, that is, double negation elimination does not hold in general in a Heyting algebra.
- The open sets of any topological space form a complete Heyting algebra. Complete Heyting algebras thus become a central object of study in pointless topology.
Quantifiers
- Totality T=1 all true; All; Or; Nor?; Nand?; And; Exists; F=0 Empty
Readings
- Philip Wadler. Propositions as Types
- Jean-Yves Girard. Proofs and Types.
- Eduardo Och's one-page introduction to lambda notation is slide 5 He updated it further with a few new slides.
- Book: Haskell Curry. Combinatory Logic, 1972.
- Notes: S2-2016: Curry-Howard correspondence
nLab
- nLab: Computational trinitarianism
- nLab: Relation between type theory and category theory
- nLab: Internal logic, nLab: Existential quantifier, nLab: Universal quantifier
- nLab: Internalization
Wikipedia
- Curry-Howard-Lambek correspondence of logic, programming and category theory
- The Calculus of constructions can be considered an extension of the Curry–Howard isomorphism. The Curry–Howard isomorphism associates a term in the simply typed lambda calculus with each natural-deduction proof in intuitionistic propositional logic. The Calculus of Constructions extends this isomorphism to proofs in the full intuitionistic predicate calculus, which includes proofs of quantified statements (which we will also call "propositions").
- Combinatory logic. Developed by Haskell Curry. Related to currying?
Notes
- John Baez, Michael Stay. Physics, Topology, Logic and Computation: A Rosetta Stone
- Correspondence: a Theory is a Category, a Model is a Functor, a Model Homomorphism is a Natural Transformation.
