Introduction E9F5FC

Questions FFFFC0

• View
• Edit
• History
• Print

Math Answers = Branches of Math

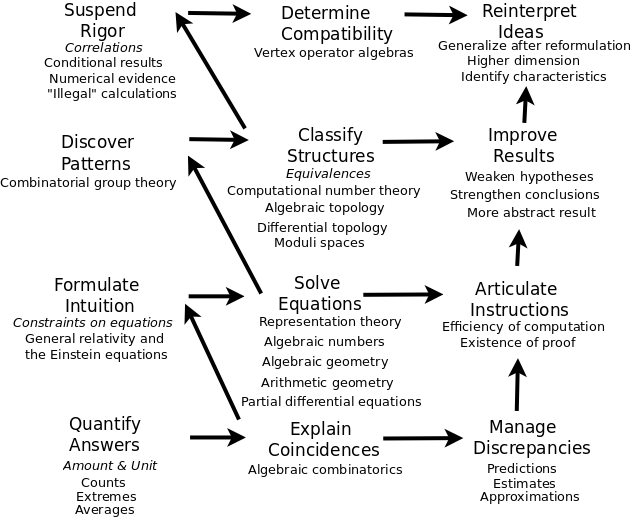
Note:

• S = The subject is defined by the kind of answer sought.
• E = The subject exemplifies the kind of answer sought.

Mathematical answers

Quantify answers

• Exact counting (Listing) S= Enumerative combinatorics (polynomial time algorithms for computation)
• Extremal problems S= Extremal Combinatorics
• Averages S= Probabilistic combinatorics

Explain coincidences

• S= Algebraic combinatorics (interpreting formulas)

Manage discrepancies

• Estimates S= Analytic number theory
• Approximations S= Numerical analysis (algorithms for approximating the continuum)
• Predictions S= Stochastic processes (model the evolution of random phenomena)

Formulate intuition as constraints on equations

• E= General relativity and the Einstein equations (expressing, interpreting and validating a theory of physics)

Solve equations. Any solutions? Unique solution? Constraints on solutions?

• Linear equations. S= Representation Theory
• Polynomial equations. S= Algebraic numbers
• Polynomial equations in several variables. S= Algebraic geometry
• Diophantine equations. S= Arithmetic geometry
• Differential equations. S= Partial differential equations

Articulate instructions. Find explicit proofs and algorithms

• S= Computational complexity (what can be computed efficiently or not)
• S= Logic and model theory (formal languages about mathematical structures, whether a proof exists or not)

Discover patterns

• S= Groups (symmetries), Combinatorial group theory (groups in terms of their generators and relations)

Classify structures.

• Building blocks and combinations. E= Computational number theory (identifying primes as components or in totality)
• Families and exceptions. E= Algebraic topology
• Transformation demonstrates equivalence. E= Differential topology (classifying smooth manifolds - list all smooth structures on any topological manifold and be able to identify them - a certain set of discrete subgroups of the isometry group of any one of the eight model spaces determines a compact manifold with the corresponding geometric structure)
• Invariant demonstrates nonequivalence. E= Algebraic topology
• Map to a structure E= Moduli spaces (give a geometric structure to the totality of the objects we are trying to classify)

Improve results

• Weaken hypotheses. E= Operator algebras (expanding from finite-dimensional equations to integral equations)
• Strengthen conclusions. E= Harmonic analysis (determining the properties of functions that are not explicitly describable, for example, the effect of operators on the boundedness of functions)
• Prove a more abstract result. E= Category theory

Suspend rigor. Work with arguments that are not fully rigorous.

• E=Conditional results = Dynamics (how systems evolve in time)
• E=Numerical evidence. = Probabilistic models of critical phenomena (modeling thresholds for divergent outcomes)
• E="Illegal" calculations. = Mirror symmetry (reformulating a physical theory's information in a mirror theory)

Determine compatibility. Whether different mathematical properties are compatible.

• E= Vertex operator algebras (formulating perspective: relating quantum data and space-time manifold)

Reintrepret ideas.

• Identify characteristic properties. E= Geometric group theory (groups in terms of their actions expressed geometrically)
• Generalize after reformulation P= Set theory (distinguishing between cardinals-sets and ordinals-lists and relating the two)
• Higher dimensions and several variables. E= High-dimensional geometry and its probabilistic analogues (most efficient boundary for volume, the sphere, models random distributions)