- MathNotebook
- MathConcepts
- StudyMath
- Geometry
- Logic
- Bott periodicity
- CategoryTheory
- FieldWithOneElement
- MathDiscovery
- Math Connections
Epistemology
- m a t h 4 w i s d o m - g m a i l
- +370 607 27 665
- My work is in the Public Domain for all to share freely.
- 读物 书 影片 维基百科
Introduction E9F5FC
Questions FFFFC0
Software
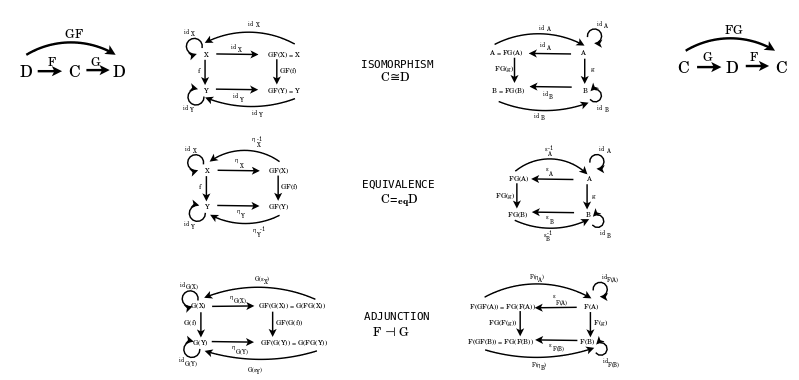
Sameness, Adjunction, Definition of adjunction, Classify adjunctions, Duality
Classify examples of equivalence and relate them to adjunctions.
Definition
- Write up: why the two definitions of equivalences (in terms of natural isomorphisms and in terms of full, faithful, essentially surjective functor) are the same and what that means in the case of two object categories.
- Compare my diagram of adjunction-equivalence-isomorphism with the template that I made for adjunction.
Classification
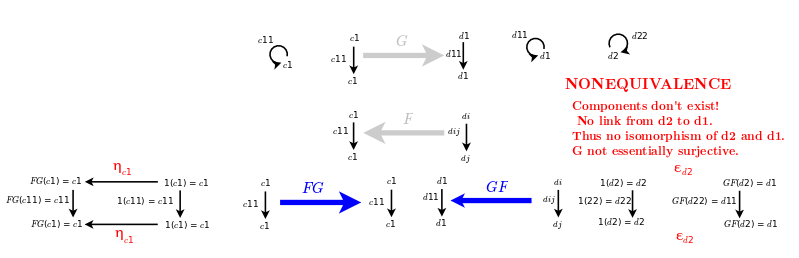
- Collect examples of equivalences that are not isomorphisms. Organize their taxonomy and relate it to the taxonomy of adjunctions.
读物
Lists of equivalences
- https://en.wikipedia.org/wiki/Equivalence_of_categories#Examples
- https://en.wikipedia.org/wiki/Equivalent_definitions_of_mathematical_structures
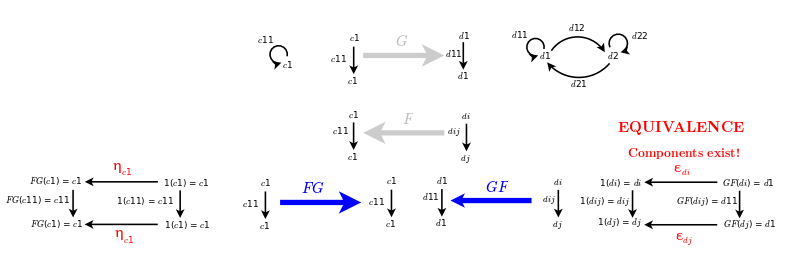
Examples of equivalences that are not isomorphisms
- Consider a discrete category without arrows. Map twice, that is a relabeling of a relabeling.
- Consider the preorder Z. Shift twice.
- Consider the preorder Z. Take it to the opposite direction. Reverse the arrows.
- Map a group to the opposite group, an element to its inverse.
- Consider various automorphisms, self-equivalences.
Consider the category {$C$} having a single object {$c$} and a single morphism {$1_c$}, and the category {$D$} with two objects {$d_1$}, {$d_2$} and four morphisms: two identity morphisms {$1_{d_1}$}, {$1_{d_2}$} and two isomorphisms {$α : d_1 \rightarrow d_2$} and {$β : d_2 \rightarrow d_1$}. The categories {$C$} and {$D$} are equivalent; we can (for example) have {$F$} map {$c$} to {$d_1$} and {$G$} map both objects of {$D$} to {$c$} and all morphisms to {$1_c$}.
- Isomorphism is based on the internal view of structures from within them. Equality considers the external view upon structures as components.
- Structures may be isomorphic but as changes are made within a system - perhaps one structure is assigned a particular role - then distinctions arise. For example, a structure may have an owner, it may be their personal property.