Math 4 Wisdom. "Mathematics for Wisdom" by Andrius Kulikauskas.

See: Math notebook, Adjunction, Category theory, Category theory glossary, Category theory progression

Investigation: Explore how limits describe external relations whereas colimits describe internal structure.

Express and compare a center and a totality in terms of limits.
Express choice frameworks in terms of limits.
Understand limits in terms of least upper bounds and greatest lower bounds, as with adjunct functors.
What is the relevance of various limits and colimits for the hierarchy of categories / logics?
Understand how a Kan extension expresses limits and colimits, as in Riehl's book 6.5.1, page 210.
What is the intuitive difference between limits and colimits and internal structure and external relationships?

Readings

Wikipedia: Limit

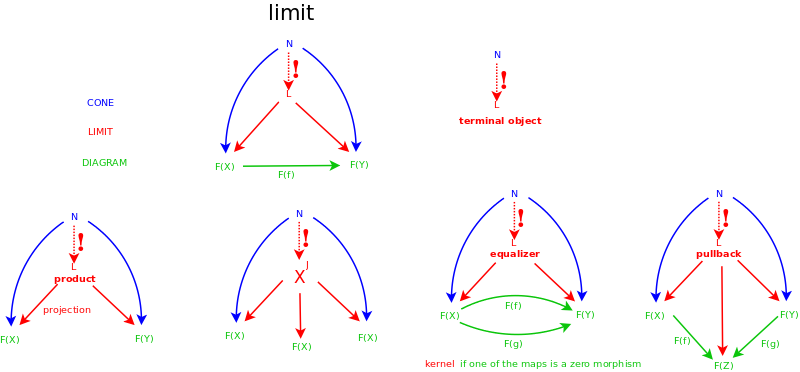
Examples

Examples of limits

products
pullbacks
inverse limits
terminal objects
equalizers, kernels

Examples of colimits

coproducts, disjoint unions, direct sums, copowers
pushouts
direct limits
initial objects
coequalizers, cokernels

Differences between limits and colimits

A cone has arrows from a limit to the objects in a diagram.
A cocone has arrows from the objects in a diagram to a limit.
Initial objects (such as the empty set) are the most primordial objects. They are the internal emptiness.
Terminal objects (such as singletons) are the most degenerate objects. They are external trivialities, like points.

Moving from internal structure to external representations - from How to What. And then we also move from the sum of external relations (why) to the inherent internal reference (Whether). So this is a (one-sided?) dual direction.

Concept of limits. Terrence Tao: Analytic limits need neighborhoods. Categorical limits need maps. Third kind of limit: Ultraproducts.

For all objects... (universality)

Exists unique = can make a definition.

Leg = action (A=A)
Syntactic A becomes semantic A. Turn the switch (the identity morphism) on or off.
(Outside) Functor pointing to A or not pointing to A.

Emily Riehl page 116 the most frequently applied result in category theory: that right adjoint functors preserve limits while left adjoint functors preserve colimits. This explains why limits tend to be easier to construct than the formally dual colimit notions.

Internal structure vs. external relationships

Coproduct of sets: Treat the sets as distinguished by labels and relabel them. In general, consider the relationship between elements and labels. Likewise, consider elements and their sequential position. Thus sets and lists ground the relationship between permutations and matrices, the permutation group and the general linear group.