• View
• Edit
• History
• Print

Wick's theorem

Wick's theorem provides the combinatorics to express an arbitrary product of creation and annihilation operators in terms of contractions (lines linking operators) and in terms of normal order (whereby all of the creation operators are subsequent (to the left) of all of the annihilation operators).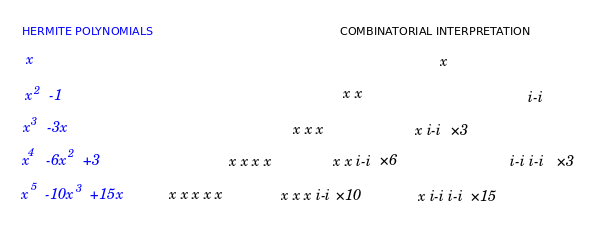

The combinatorics of Wick's theorem is basically the same as the combinatorics of the Hermite polynomials.

Several ideas come to mind.

• Momentum is expressed by a pair of creation and annihilation operators. We can think of momentum as indicating that a particle disappears and then reappears.
• In the case of fermions, we include a factor of {$i^2=-1$}. Presumably this is because an existing particle disappeared in one location and reappeared in another location. Apparently, this inverts the understanding of energy. Whereas if it appeared and disappeared then that has no bearing.
• In the case of bosons, an existing particle may disappear in one location but reappear in the same location. This has no bearing on energy. The factor is {$1$}.
• In either case, the space is not free but rather something is happening there. Thus it does not incur the cost of free space which is given by the variable {$x$}.
• The operators that are neither creation nor annihilation operators are unpaired saplings. They each get weight {$x$} because they represent cells of free space. An observer carves out that free space.

Questions

• Do the Charlier polynomials express the creation and annihilation operators for bosons?
• Do Feynman diagrams express Zeng saplings?