- MathNotebook
- MathConcepts
- StudyMath
- Geometry
- Logic
- Bott periodicity
- CategoryTheory
- FieldWithOneElement
- MathDiscovery
- Math Connections
Epistemology
- m a t h 4 w i s d o m - g m a i l
- +370 607 27 665
- My work is in the Public Domain for all to share freely.
- 读物 书 影片 维基百科
Introduction E9F5FC
Questions FFFFC0
Software
Yoneda lemma, Yoneda Lemma Slides, Yoneda Embedding Abstract, Yoneda Embedding Foursome
Presentation for Thomas, John, Michael
For my talk
- Do the four levels apply to morphisms or something more?
- How can we understand the two conceptions of the foursome in terms of observer and observed?
- How do the validations appear if we use the Yoneda embedding as the functor?
- What does validation mean?
- In what sense does the Yoneda Lemma work like the Homset adjunction?
- In what sense can the Yoneda Lemma or the Yoneda embedding be understood as an adjunction?
- How to understand the relationship between cognition and emotion as an adjunction? What does this say about adjunction in general?
- How to interpret the natural transformation {$\psi^u$} as an imposition of the Conscious on the Unconscious?
- What does it mean to consider {$\psi^u$} for a particular {$u\in F(A)$}? and for all {$u\in F(A)$}? And for all {$u$}, {$A$} and {$F$}?
- What is the difference between trivial actions (defined by adjunctions) and the null action (defined by the Yoneda lemma)?
{$\textrm{Hom}(\textrm{Hom}(A,\_),\textrm{Hom}(B,\_))\cong\textrm{Hom}(B,A)$}
| Why is {$B\overset{u}{\rightarrow}A$} | {$\theta^{B\overset{u}{\rightarrow}A}_X(A\overset{f}{\rightarrow}X)=B\overset{u}{\rightarrow}A\overset{f}{\rightarrow}X$} | all possible ways of extending {$B\overset{u}{\rightarrow}A$} beyond {$A$} |
| How is {$B\overset{u}{\rightarrow}A$} | {$\theta^{B\overset{u}{\rightarrow}A}\in\textrm{Hom}(\textrm{Hom}(A,\_),\textrm{Hom}(B,\_))$} | the particular action of prepending {$B\overset{u}{\rightarrow}A$} to any morphism {$A\overset{f}{\rightarrow}X$} |
| What is {$B\overset{u}{\rightarrow}A$} | {$B\overset{u}{\rightarrow}A\in\textrm{Hom}(B,A)$} | an element in an output: a particular route {$u$} from a fixed {$B$} to a variable {$A$} |
| Whether is {$B\overset{u}{\rightarrow}A$} | {$\theta^{B\overset{u}{\rightarrow}A}(A\overset{\textrm{id}_A}{\rightarrow}A)=B\overset{u}{\rightarrow}A$} | the output of a particular natural transformation upon the do-nothing action for object {$A$} |
The Knowledge Switch
The Yoneda Lemma asserts the compatibility of the validation of emotional truth and the cognitive articulation of worldview
The Yoneda Lemma thereby relates four levels of knowledge: Whether, What, How, Why.
I will present the Yoneda Lemma and my interpretation of it by explaining it and reexplaining it in ever more detail.
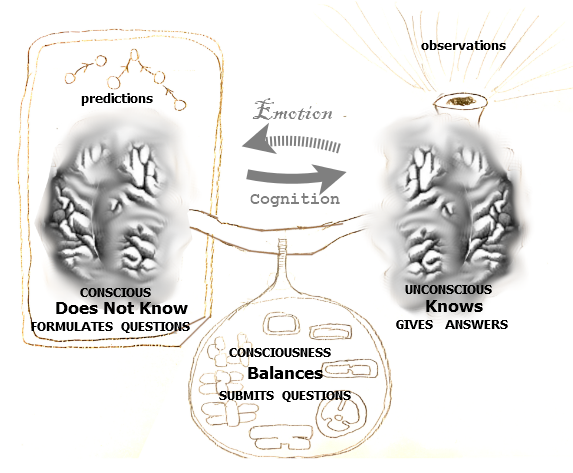
The Conscious imposes Cognition on the Unconscious
Cognition is the way that the Conscious communicates with the Unconscious, whereas Emotion is the way that the Unconscious communicates with the Conscious. We can say that Cognition is an imposition of the Conscious upon the Unconscious. Cognition imposes a language of concepts upon the Unconscious. When the imposition is satisfactory, then we are at Peace. But as circumstances change, for reasons random or regular, the concepts are not satisfactory, and we experience emotion. Then Cognition adjusts its language of concepts and reimposes it.
Yoneda Lemma Equates Cognition and Emotion
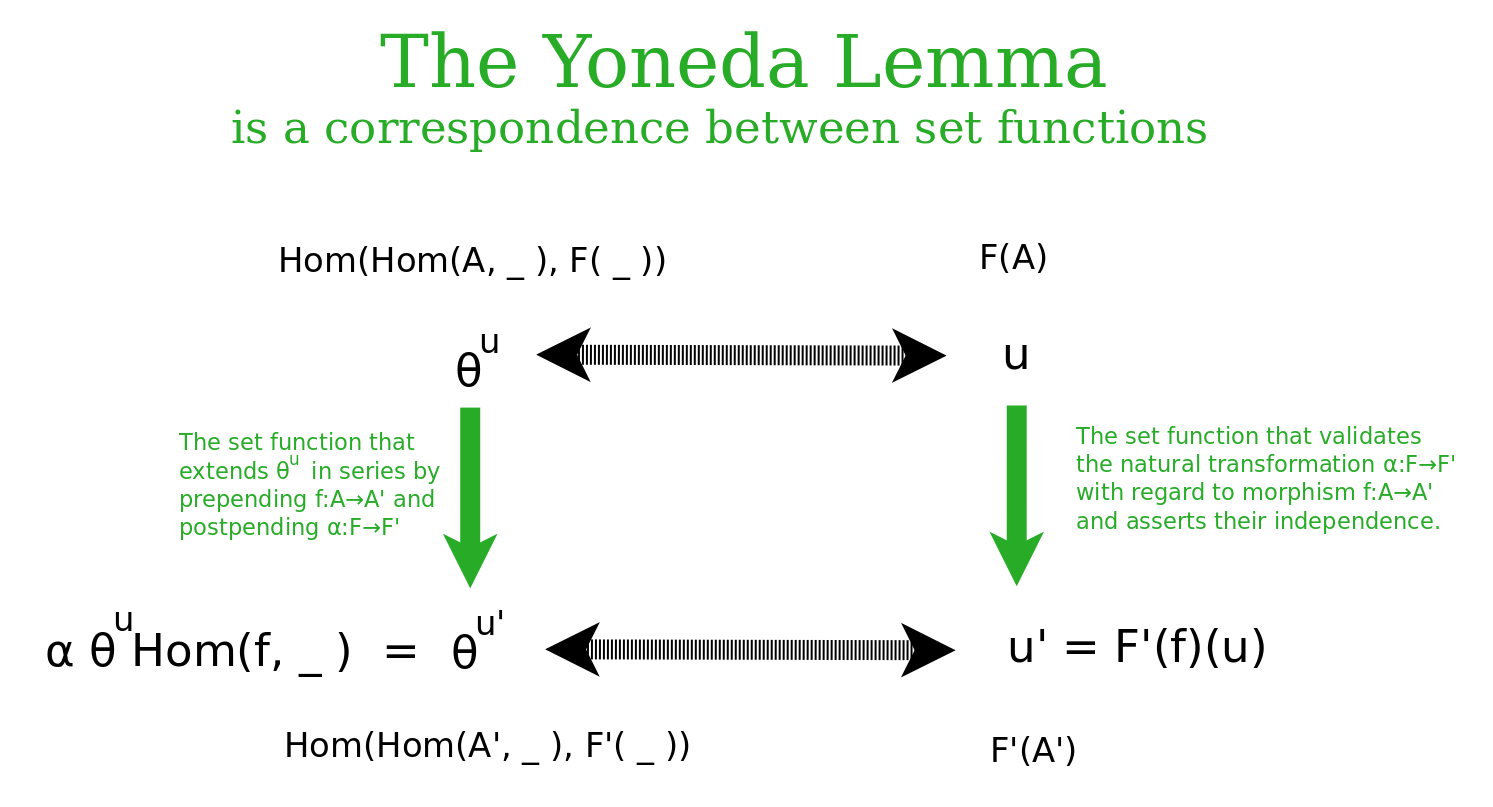
The Yoneda Lemma describes a natural isomorphism. {$\textrm{Hom}(\textrm{Hom}(A,\_),F)\cong F(A)$}
Thus it provides two different but equivalent views on the same thing.
The view {$\textrm{Hom}(\textrm{Hom}(A,\_),F)$} describes Cognition.
The view {$F(A)$} describes Emotion.
Cognition and Emotion are Functors of the form {$C\times\textrm{Set}^C\rightarrow\textrm{Set}$}
Functors are maps which are defined on maps and return maps.
Cognition and Emotion are functors. They are isomorphic as functors.
They have two arguments as inputs. They each take a question {$f:A\rightarrow A'$} and an enlightenment {$\alpha:F\rightarrow F'$}. They output set functions.
The Input consists of a Question and an Enlightment
Cognition and Emotion have two arguments as inputs.
The first argument is a question of the form {$f:A\rightarrow A'$} where {$A$} and {$A'$} are topics, {$A$} is the context for {$A'$}, and {$f$} is a question about {$A'$} in the context {$A$}. Here a question may be thought of as an interrogation of the form, Given {$A$}, what about {$A'$}?
The second argument is an enlightenment of the form {$\alpha:F\rightarrow F'$} where {$F$} and {$F'$} are understandings.
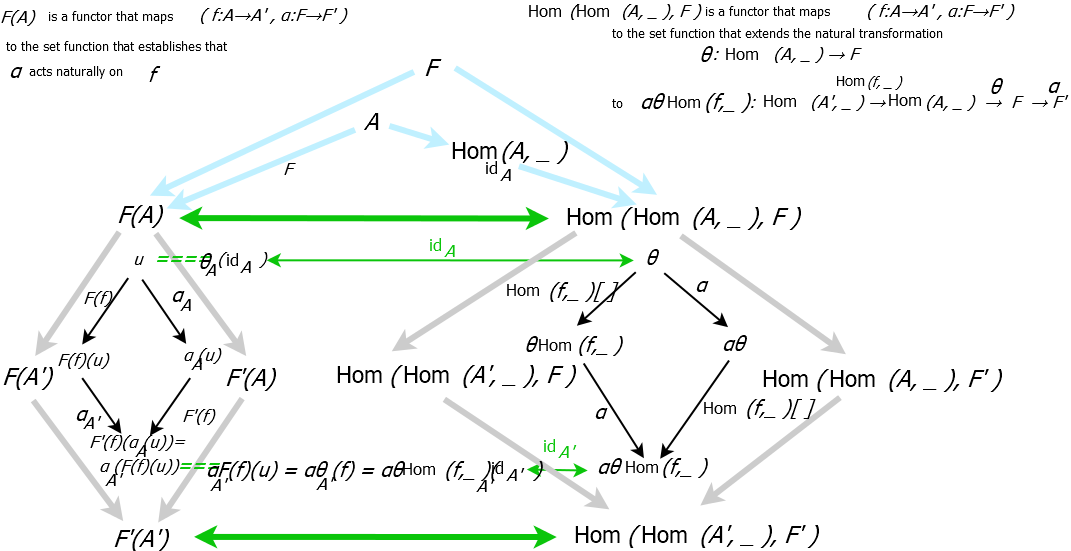
For example, {$F$} takes a question {$f:A\rightarrow A'$} and returns an implication {$F(f):F(A)\rightarrow F(A')$} that takes us from the set of facts {$F(A)$} about {$A$} to another set of facts {$F(A')$} about {$A'$}.
Consequently, an enlightenment {$\alpha$} takes us from the understanding {$F$} to a new understanding {$F'$} of that same question {$f$} as a new implication {$F'(f)$} relating new sets of facts {$F'(A)$} and {$F'(A')$}.
Cognition and Emotion output set functions.
Emotion outputs the emotional truth.
Suppose we are given a question {$f:A\rightarrow A'$} and an enlightenment {$\alpha:F\rightarrow F'$}.
Emotion outputs the set function which send {$u\in F(A)$} to {$F'(f)(\alpha_A(u))=\alpha_{A'}(F(f)(u))\in F'(A')$}. This is the set function which establishes that the enlightenment {$\alpha$} acts naturally on the question {$f$}. In other words, Emotion outputs the implication which establishes the independence of the question and the enlightenment in relating the facts {$F(A)$} with the subsequent facts {$F'(A')$}, and thus the accordance {$F'(f)(\alpha_A(u))=\alpha_{A'}(F(f)(u))$}, which is independent of the order, whether we first ask or whether we are first enlightened. This set function is thus the emotional truth. Emotion takes a question and an enlightenment and outputs the emotional truth, which is a function on {$u\in F(A)$} that brings us to {$F'(A')$}. Note that emotion does not output what is not the emotional truth!
Cognition outputs the set function from {$\textrm{Hom}(\textrm{Hom}(A,\_),F)$} to {$\textrm{Hom}(\textrm{Hom}(A',\_),F')$} which maps the natural transformation {$\psi_u$} to the natural transformation {$\psi^{u'}=\alpha \psi^u \textrm{Hom}(f,\_)$}. Which is to say, cognition prepends the question and postpends the enlightenment. So what is the natural transformation {$\psi_u$}? It is the worldview which the Conscious imposes on the Unconscious. Thus Cognition outputs a cognitive articulation {$\alpha \psi^u \textrm{Hom}(f,\_)$} of the worldview {$\psi^u$}.
The Yoneda Lemma equates the Cognitive Articulation of {$\psi^u $} with the Emotional Truth about {$u$}
Conscious {$\{ f\; |\; A\overset{f}{\rightarrow} X\} $} and Unconscious {$F(X)$} are functors
The Conscious and the Unconscious are two minds, two hemispheres.
- Unconscious knows, thus gives answers.
- Conscious does not know, thus asks questions.
Both minds are functors from the category {$C$} to the category {$\textrm{Set}$}. What do the categories mean? They are worlds and consist of morphisms relating objects. The world {$C$} is made of morphisms {$A\overset{f}{\rightarrow}B$} and these express the mental model, the conceptual language, the web of questions that the Conscious organizes. The world {$\textrm{Set}$} expresses the interface with the facts of the "real world", which may be the possible answers to the questions, thus sets of answers.
Thus the Conscious mind takes us from objects (topics) {$X$} to arrows (questions) {$f:A\rightarrow X$} relative to a chosen object (context) {$A$}. In this understanding, each arrow {$f$} is a question about topic {$X$} relative to some context {$A$}. Mathematically, Conscious is a functor {$\{ f\; |\; A\overset{f}{\rightarrow} X\} $} which takes an object {$X$} in a world {$C$} and returns the set {$\{ f\; |\; A\overset{f}{\rightarrow} X\} $} of arrows {$f$} from object {$A$} to {$X$}.
The Unconscious mind takes us from objects (topics) {$X$} to sets {$F(X)$} which can be interpreted as sets of answers (facts) about {$X$}.
Thus the Unconscious interprets experience {$F(X)$} directly through a topic {$X$} that offers a unifying perspective on everything, thus a first level of reflection.
The Conscious interprets and understands by navigating the conceptual language as a traveling context {$A$}, which serves as a personal point of reference, thus a second perspective, a second level of reflection.
Cognition {$\psi^u$} imposes the Conscious {$\{ f\; |\; A\overset{f}{\rightarrow} X\} $} on the Unconscious {$F(X)$}
The Yoneda Lemma explains how, for the Unconscious, we can change the level of experience with a deeper level of experience {$F(X)\rightarrow F'(X)$}, when for the Conscious, we change the context from {$A$} to {$A'$} or not.
Mathematically, given a category (a world) {$C$}, fix an object {$A$} in {$C$}, and fix a functor {$F:C\rightarrow\textrm{Set}$}. We fix {$A$} and {$F$} but then we also allow them to change {$A\overset{f}{\rightarrow}A'$}, {$F\overset{\eta}{\rightarrow}F'$}.
The imposition {$\psi^u $} can be intrinsic, hard-wired, whereby How precedes What, as in "form follows function", equivalently, function {$\{ f\; |\; A\overset{f}{\rightarrow} X\} $} precedes form {$F(X)$}.
Alternatively, this imposition can be made extrinsic, soft-wired, whereby we peel away a layer of the onion from the unknowing outside Pre and likewise from the knowing inside Post, so that we have Post-Psi-Pre, which is to say, around an intrinsic middle {$\psi^{u'}$} we make explicit the Conscious's pre-composition of conceptual relationships {$A\rightarrow A' $} to know Why and the Unconscious's post-composition of interpretations {$F'\rightarrow F $} to know Whether.
Which is to say, Why and Whether provide context for How and What, making that context explicit. Simply put, we shift from a view (How to What) where we have to intrinsically handle everything, all compositional implications, all at once, to a view (Why to Whether) where we instead allow for subroutines by which we can separately consider validity in terms of movement from initial states to terminal states.
The Yoneda Lemma says that the two views are equivalent, yet mentally we only experience the movement from How-What to the more explicit Why-Whether.
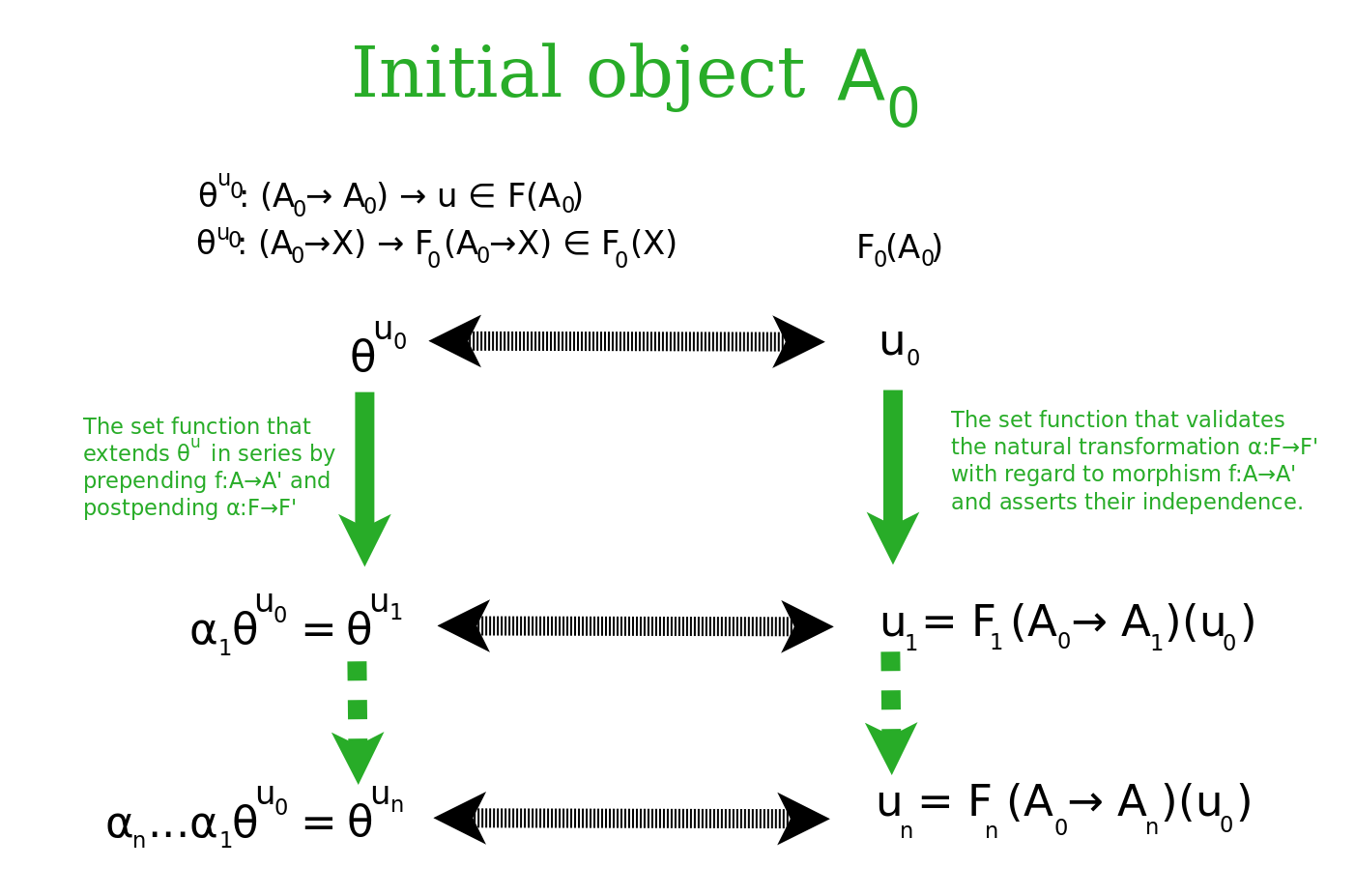
The Infinite Regress
The functors {$F(A)$} and {$\textrm{Hom}(\textrm{Hom}(A,\_),F)$} can have the following form.
They are a general construction "F(A)" which takes the building blocks "(A,F)" and yields a particular rule "F(A)". Thus they have the form:
{$C\times\textrm{Set}^C\rightarrow((C\times\textrm{Set}^C)\rightarrow\textrm{Set})$}
And similarly we can take each generalization "F(A)" and consider the functor from "(A,F)" to this "F(A)". We can proceed this way infinitely. This is the essence of abstraction.
Definition of natural isomorphism
A natural isomorphism {$\eta:F\rightarrow G$} is a natural transformation which works in both directions because each component {$\eta_X$} is an isomorphism, thus has an inverse morphism {$\eta^{-1}_X$}, whereby {$\eta_X\eta^{-1}_X=1_{G(X)}$} and {$\eta^{-1}_X\eta_X=1_{F(X)}$}. Our functors go into the category of sets, {$\textrm{Set}$}, and so the components {$\eta_X$} are set functions, and being isomorphisms, they are bijections.
Associativity
Commutative diagrams are about associativity. They should be called associativity diagrams.
The Yoneda Lemma is about two ways of looking at associativity.
Jesus
The Yoneda Lemma expresses Jesus's commands
- Love God (with all of your heart, will, soul, body) (God is the absolute context, the key answer, whether there is context)
- Love your neighbor as yourself (neighbor is proximate, establishes geometry, probes)
Criteria
The Yoneda Lemma relates six set functions - two go down and four go across. Do these express the six criteria?
Natural transformations
Two natural transformations {$\alpha_1:F\rightarrow G$} and {$\alpha_2:F\rightarrow G$} have their components defined on the same objects {${\alpha_1}_X:F(X)\rightarrow G(X)$} and {${\alpha_2}_X:F(X)\rightarrow G(X)$}. However, the components {${\alpha_1}_X$} and {${\alpha_2}_X$} may differ as morphisms. Yet in the case of a preorder there is at most one morphism and so both natural transformations refer to the same morphism. Also, in the case of natural isomorphisms, ...
Examples of natural transformations
Determinant
Consider the category {$\mathbf{CRing}$} of commutative rings and the category {$\mathbf{Grp}$} of groups. We can define the following two functors from {$\mathbf{CRing}$} to {$\mathbf{Grp}$}. The functor {$\textrm{GL}_n(\_)$} takes a ring to the group of invertible {$n\times n$} matrices of ring elements and likewise lifts a ring homomorphism to a linear transformation. The functor {$\_*$} takes a ring to the group of units (invertible elements) for the ring and likewise restricts a ring homomorphism to the units. The determinant is a natural transformation from the one functor to the other, satisfying the following commutative diagram, where {$f:R\rightarrow S$} is a ring homomorphism.
{$\begin{matrix}\textrm{GL}_n(R) & \overset{\textrm{det}_R}\longrightarrow & R* \\ \textrm{GL}_n(f)\downarrow & & \downarrow f*\\ \textrm{GL}_n(S) & \overset{\textrm{det}_S}\longrightarrow & S* \end{matrix}$}
Endofunctor
Given an endofunctor, that is, a functor F that maps a category to that same category, then there is a natural transformation α \alpha from the identity functor to that functor, with components α C = F ( C ) {\displaystyle \alpha _{C}=F(C)}.
{$\begin{matrix}C & \overset{\alpha_C=F(C)}\longrightarrow & F(C) \\ f\downarrow & & \downarrow F(f)\\ D & \overset{\alpha_D=F(D)}\longrightarrow & F(D) \end{matrix}$}
Opposite group
Every group is naturally isomorphic to its opposite group.
Double dual of a vector space
Here is an example of an endofunctor. Consider the category {$\mathbf{Vect}$} of vector spaces over {$K$} with linear maps. We can define the following two functors from {$\mathbf{Vect}$} into {$\mathbf{Vect}$}. We have the identity functor and we also have the double dual functor {$\Psi_U$}, which maps {$U$} into {$U'' = \{\phi:U'\rightarrow K \;|\; \phi \textrm{ linear }\}$} by setting {$\Psi(u):\phi\rightarrow\phi(u)$}, which is to say, {$\Psi(u):<a_U,\;\_>\rightarrow <a_U,u>$}. Then there is a natural transformation from the identity functor to the double dual functor.
{$\begin{matrix} U & \overset{\Psi_U:u\rightarrow [<a_U,\;\_>\rightarrow <a_U,u>]}\longrightarrow & U'' \\ f:u\rightarrow v\downarrow & & \downarrow f'':[<a_U,\;\_>\rightarrow <a_U,b_U>]\rightarrow [<f(a_U),\;\_>\rightarrow <f(a_U),f(b_U)>]\\ V & \overset{\Psi_V:v\rightarrow [<a_V,\;\_>\rightarrow <a_V,v>]}\longrightarrow & V'' \end{matrix}$}
Applications of the Yoneda Lemma
Preorders
A preorder is a category for which there is at most one morphism between any two objects.
Thus {$\textrm{Hom}(A,X)=\{A\rightarrow X\}$} or {$\varnothing$} and we can write
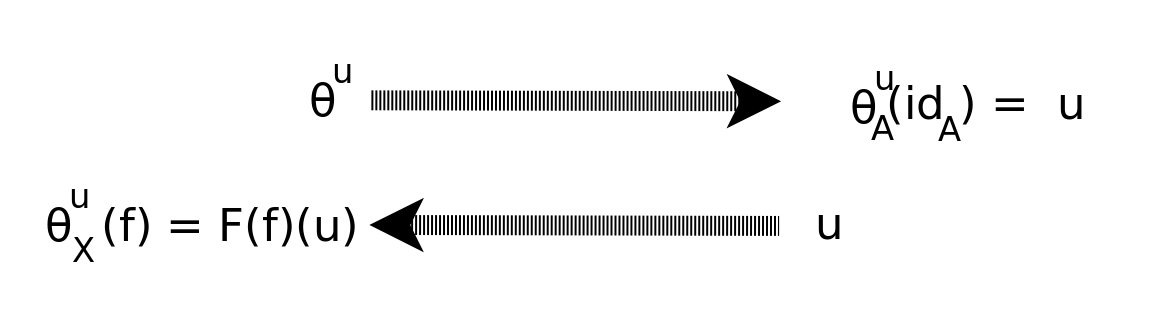
{$\theta^u_A:(A\rightarrow A)\rightarrow u\in F(A)$}
{$f=(A\rightarrow X)$}
{$F(f):F(A)\rightarrow F(X)$}
{$F(A\rightarrow X):F(A)\rightarrow F(X)$}
{$\theta^u_X:(A\rightarrow X)\rightarrow w = F(A\rightarrow X)(u) \in F(X)$}
{$\theta^u_X:\varnothing\rightarrow F(X)$} is the empty function
We can write out the commutative diagram
{$\begin{matrix}\{A\rightarrow X\} & \overset{\theta^u_X}\longrightarrow & F(A\rightarrow X)(u)\in F(X) \\ \textrm{postpend }f:X\rightarrow Y\downarrow & & \downarrow F(f)\\ \{A\rightarrow Y\} & \overset{\theta^u_Y}\longrightarrow & F(A\rightarrow Y)(u)\in F(Y) \end{matrix}$}
Preorders with {$F(X) = \textrm{Hom}(B,X)$}
Yoneda lemma is then {$\textrm{Hom}(\textrm{Hom}(A,\_),\textrm{Hom}(B,\_)\cong\textrm{Hom}(B,A)$}
{$\textrm{Hom}(\{A\rightarrow \_\}, \{B\rightarrow \})\cong \{B\rightarrow A\}$}
{$\forall X [\theta^u_X:\{A\rightarrow X\}\rightarrow \{B\rightarrow X\}]\Leftrightarrow \{B\rightarrow A\}=u$}
{$\theta^u_X$} appends {$(B\rightarrow A)=u $}
The Yoneda Lemma here can be understood as {$\forall X [A\geq X\Rightarrow B\geq X]\Leftrightarrow B\geq A$}
Similarly, {$\forall X [A\rightarrow X\Rightarrow F(X)]\Leftrightarrow F(A)$}
For if {$\forall X [A\rightarrow X\Rightarrow F(X)]$} then let {$X=A$} and since the identity morphism {$A\rightarrow A$} exists, we conclude {$F(A)$}.
And if {$F(A)$}, we also know that {$A\rightarrow X$} implies {$F(A\rightarrow X)$} and taken together this implies {$F(X)$}.
Preorders - the natural isomorphism
Yoneda lemma is {$\textrm{Hom}(\textrm{Hom}(A,\_),\textrm{Hom}(B,\_)\cong\textrm{Hom}(B,A)$} but we also have
{$\textrm{Hom}(\textrm{Hom}(A',\_),\textrm{Hom}(B',\_)\cong\textrm{Hom}(B',A')$}
where we prepend {$A\rightarrow A'$}
and postpending {$\alpha:\textrm{Hom}(B,\_)\rightarrow\textrm{Hom}(B',\_)$} works by prepending {$B'\rightarrow B$}.
Group {$G$}
A group {$G$} can be thought of as a category with a single object {$*$} and with the morphisms being the elements of the group. The identity element is the identity moprhism {$e=\textrm{id}_*$}.
Yoneda Embedding - Adjunction
Yoneda embedding
Yoneda embedding is the embedding of a category {$\mathcal{C}$} into {$\mathbf{Set}$} as follows:
{$\mathcal{C}(A,B) \simeq \mathbf{Set}(\mathcal{C}(-,B),\mathcal{C}(-,A))$}
The category C is identified with a tiny portion of Set and, in that sense, is embedded within it.
So we can think of the Yoneda embedding as a fully faithful functor {$Z:\mathcal{C}\rightarrow \mathbf{Set}^{\mathcal{C}}$} which sends {$X$} to the functor {$\mathcal{C}(-,X)$} and which sends {$f:X\rightarrow Y$} to the natural transformation which sends functor {$\mathcal{C}(-,Y)$} to {$\mathcal{C}(-,X)$} by prepending {$f$}.
nLab: Adjoint string There is an adjoint 5-tuple between {$[Set^{op}, Set]$} and {$Set$}. Indeed, given a locally small category B, and the Yoneda embedding, {$Y: B \to [B^{op}, Set]$}, then Y being the rightmost functor of an adjoint 5-tuple entails that B is equivalent to Set; see Rosebrugh, Wood. An Adjoint Characterization of the Category of Sets and also Ross Street, Robert Walters. Yoneda Structures on 2-Categories.
Definition of adjunction
A hom-set adjunction between two categories C and D consists of two functors {$F:D\rightarrow C$} and {$G:C\rightarrow D$} and a natural isomorphism {$\Phi:\mathrm{hom}_C(F-,-) \to \mathrm{hom}_D(-,G-)$}. This specifies a family of bijections {$\Phi_{Y,X}:\mathrm{hom}_C(FY,X) \to \mathrm{hom}_D(Y,GX)$} for all objects X in C and Y in D.
In this situation, F is left adjoint to G and G is right adjoint to F.
In what sense is the Yoneda Lemma an adjunction?
{$\textrm{Hom}(\textrm{Hom}(A,\_),F)\cong F(A)$}
{$\textrm{Hom}(\textrm{Hom}(A,\_),\textrm{Hom}(B,\_))\cong \textrm{Hom}(B,A)$}
Compare with the Tensor-Hom adjunction
{$\operatorname{Hom}(Y\otimes X,Z)\cong \operatorname{Hom}(Y,\operatorname{Hom}(X,Z))$} where {$X$} is fixed and {$Y$} and {$Z$} vary.
Why is the fact that we extract the action (natural transformation} {$\theta^u$} from the composition of arrows.
Whether is based on the identity. Why is based on associativity, on composition - closure - that the logic of arrows exists.
Sets express possibility. What gives the possible arrow. How has us choose an actual arrow. Why gives the logic by which an arrow is necessary.
Note that for How the sequence is clear. First we have A->X and then we extend B->A->X.
Note that for Whether the sequence is clear. First we have A->A and then we extend B->A->A.
Understand
Propositional functions
{$P\leq Q\Leftrightarrow \forall X(P(X)\Rightarrow Q(X))$}
{$\Omega^X$} is the set of propositional functions {$P:X\rightarrow \Omega$}
Short exact sequence in terms of Whether, What, How, Why
Yoneda embedding. Adjoint 5-tuple between {$[Set^{op}, Set]$} and {$Set$}
Yoneda embedding is the embedding of a category {$\mathcal{C}$} into {$\mathbf{Set}$} as follows:
{$\mathcal{C}(A,B) \simeq \mathbf{Set}(\mathcal{C}(-,B),\mathcal{C}(-,A))$}
So we can think of the Yoneda embedding as a fully faithful functor {$Z:\mathcal{C}\rightarrow \mathbf{Set}^{\mathcal{C}}$} which sends {$X$} to the functor {$\mathcal{C}(-,X)$} and which sends {$f:X\rightarrow Y$} to the natural transformation which sends functor {$\mathcal{C}(-,Y)$} to {$\mathcal{C}(-,X)$} by prepending {$f$}.
nLab: Adjoint string There is an adjoint 5-tuple between {$[Set^{op}, Set]$} and {$Set$}. Indeed, given a locally small category B, and the Yoneda embedding, {$Y: B \to [B^{op}, Set]$}, then Y being the rightmost functor of an adjoint 5-tuple entails that B is equivalent to Set; see Rosebrugh, Wood. An Adjoint Characterization of the Category of Sets and also Ross Street, Robert Walters. Yoneda Structures on 2-Categories.
Related chat on the Category Theory Zulip server
There is an adjoint string {$\mathbf{0}\vdash\mathbf{!}\vdash\mathbf{1}:\mathbf{1}\rightarrow\mathbf{Set}$} where the category {$\mathbf{1}$} has one object and one morphism (the identity morphism), where {$\mathbf{0}:\mathbf{1}\rightarrow\mathbf{Set}$} is the constant functor which sends that category's object to the empty set, where {$\mathbf{!}:\mathbf{Set}\rightarrow\mathbf{1}$} sends any set to the category's object and sends any set function to the identity morphism, and where {$\mathbf{1}:\mathbf{1}\rightarrow\mathbf{Set}$} is the constant functor which sends that category's object to a singleton.
We can apply the Yoneda embedding {$\mathcal{M}$} to that entire adjoint string. We get {$\mathcal{M}\mathbf{0}\vdash\mathcal{M}\mathbf{!}\vdash\mathcal{M}\mathbf{1}:\mathcal{M}\mathbf{Set}\rightarrow\mathbf{Set}$}. Note that {$\mathcal{M}$} flips everything around. And then we can extend the adjoint string.
Note that the object {$\mathcal{M}\mathbf{1}\cong\mathbf{Set}$}.
Thus the constant functor {$\mathbf{0}:\mathbf{1}\rightarrow\mathbf{Set}$} becomes {$\mathcal{M}\mathbf{0}:\mathcal{M}\mathbf{Set}\rightarrow\mathbf{Set}$}
The unique functor {$\mathbf{!}:\mathbf{Set}\rightarrow\mathbf{1}$} becomes {$\mathcal{M}\mathbf{!}:\mathbf{Set}\rightarrow\mathcal{M}\mathbf{Set}$}.
The constant functor {$\mathbf{1}:\mathbf{1}\rightarrow\mathbf{Set}$} becomes {$\mathcal{M}\mathbf{1}:\mathcal{M}\mathbf{Set}\rightarrow\mathbf{Set}$}
Tensor-Hom Adjunction
Hom functor outputs values in Set, whereas Internal Hom outputs values in the category C. They both take inputs from {$C^{op}\times C$}. A category with Internal Hom is called a closed category. They are closely related to the Yoneda lemma. Examples include cartesian closed categories (Set, or any topos), compact closed categories (notably finite dimensional vector spaces FdVect), monoidal closed categories.
Tensor product increases slack because it makes all of the factors equally available. Internal Hom decreases slack because it tucks them away one by one in a definite order.
Tensor product expresses geometry (homogeneous choice). Internal Hom expresses algebra (thinking step-by-step).
The tensor-curry adjunction relates all and one, as between everything and anything, and between nothing and something. It allows for step-by-step algebra, as by the Yoneda lemma.
nLab: Yoneda Lemma (Yoneda embedding is adjunct of hom-functor) The Yoneda embedding functor {$y:𝒞→[𝒞^{op},\textrm{Set}]$} from Def. 2.1 is equivalently the adjunct of the hom-functor {$\textrm{Hom}_𝒞:𝒞^{op}×𝒞⟶\textrm{Set}$} under the product category/functor category adjunction {$\textrm{Hom}(C^{op}×C,\textrm{Set})\overset{≃}{→}\textrm{Hom}(C,[C^{op},\textrm{Set}])$} in the closed symmetric monoidal category of categories.
Ext is related to the  Yoneda product
Yoneda product
Isbell Duality
{$(𝒪⊣Spec):CoPresheaves\overset{𝒪}{\underset{Spec}{⇆}}Presheaves$}
Spec is the left Kan extension of the Yoneda embedding along the contravariant Yoneda embedding, while 𝒪 is the left Kan extension of the contravariant Yoneda embedding along the Yoneda embedding.
In the simplest case, namely for an ordinary category {$\mathcal{C}$}, the adjunction between presheaves and copresheaves arises as follows...
- The presheaf category {$[\mathcal{C}^{op}, \mathrm{Set}]$} has all limits, so we can extend the Yoneda embedding to a continuous functor
{$Y \colon [\mathcal{C}, \mathrm{Set}]^{op} \to [\mathcal{C}^{op}, \mathrm{Set}]$} from copresheaves to presheaves.
- Dually, the copresheaf category {$[\mathcal{C}, \mathrm{Set}]^{op}$} has all colimits, so we can extend the co-Yoneda embedding to a cocontinuous functor {$Z \colon [\mathcal{C}^{op}, \mathrm{Set}] \to [\mathcal{C}, \mathrm{Set}]^{op}$} from presheaves to copresheaves.
- Isbell duality says that these are adjoint functors: Y is right adjoint to Z.
The more general case deals with enrichment.
nLab: Spec is the left Kan extension of the Yoneda embedding along the contravariant Yoneda embedding, while {$\mathcal{O}$} is the left Kan extension of the contravariant Yoneda embedding along the Yoneda embedding.
nLab: The codensity monad of the Yoneda embedding is isomorphic to the monad induced by the Isbell adjunction, {$Spec \mathcal{O}$} (Di Liberti 19, Thrm 2.7).
Geometry and algebra as duals by way of adjunctions
- “Make the popular heuristic that geometry and algebra are two sides of the same coin precise in the framework of category theory!” Following William T. Lawvere, (generalized) spaces can be formalized as presheaves and (generalized) algebras of functions over a space as co-presheaves. In the special case of enriched (co-)presheaves the left Kan extensions of the covariant and contravariant enriched Yoneda-embeddings along each other then define an enriched adjunction between spaces and function algebras, the Isbell conjugacy. More generally, the theory of the Isbell envelope allows reasoning about whether two categories satisfy such a notion of Isbell duality. Knowledge of topic no. 4 has to be considered a prerequisite. Though not strictly necessary, understanding a bit of topic no. 16 will be helpful. [Isb66]
nLab: duality between algebra and geometry
- nLab: The duality relevant to the spectral theory is the duality commutative von Neumann algebras and compact strictly localizable enhanced measurable spaces.
 Equivalence of categories One of the central themes of algebraic geometry is the duality of the category of affine schemes and the category of commutative rings. The functor G {\displaystyle G} G associates to every commutative ring its spectrum, the scheme defined by the prime ideals of the ring. Its adjoint F {\displaystyle F} F associates to every affine scheme its ring of global sections.
Equivalence of categories One of the central themes of algebraic geometry is the duality of the category of affine schemes and the category of commutative rings. The functor G {\displaystyle G} G associates to every commutative ring its spectrum, the scheme defined by the prime ideals of the ring. Its adjoint F {\displaystyle F} F associates to every affine scheme its ring of global sections.Probing objects with the Yoneda Lemma
Application of Yoneda Lemma to make conclusions about a category
Riehl page 115: The universal property of the free vector space functor {$\mathbb{k}[−]:\textbf{Set}\rightarrow\textbf{Vect}_k$} is expressed by saying that it is left adjoint to the underlying set functor {$U:\textbf{Vect}_k\rightarrow\textbf{Set}$}: linear maps {$\mathbb{k}[S]\rightarrow\mathbf{V}$} correspond naturally to functions {$S\rightarrow U(V)$}, which specify the image of the basis vectors {$S⊂\mathbb{k}[S]$}. By the Yoneda lemma, this universal property can be used to define the action of the free vector space functor {$\mathbb{k}[−]$} on maps. The forgetful functor {$U:\textbf{Vect}_k\rightarrow\textbf{Set}$} has no right adjoint, so in this setting there are no competing notions of free construction.
Exactness, adjunctions, Yoneda lemma
Paul Garrett. Adjoints, naturality, exactness, small Yoneda lemma The proof that left adjoints are right-exact, and that right adjoints are left-exact, uses a small incarnation of Yoneda’s Lemma, and illustrates the importance of naturality of isomorphisms.
A personal quest - which shows the relevance of category theory in the humanities - which may have more of the rigor of poetry than of mathematics - and yet may be precise in areas where mathematics is not. Also, it may yield insight as to how various problems in math may be related.
Seek clarity about the kinds of knowledge, the levels of knowledge. Those levels that are essential to distinguish for there to be knowledge at all.
Reasons to believe that there is a cognitive framework, the foursome, for knowledge.
Can consider classic distinctions.
Will describe a heuristic, nonaxiomatic.
Absolute truth as an attitude.
Contemplation of the limits of the imagination.
Explore the possible meaning of absolute truth.
Appeal to mathematics as less subjective grounds.
Start with a contradiction as with assigning a name to the do-nothing action, which is to say, to the identity map.
Why u:B->A? It is a context for understanding why A in terms of the paths from B to all manner of X.