Introduction

Notes

Math

Epistemology

Search

Andrius Kulikauskas

  • m a t h 4 w i s d o m - g m a i l
  • +370 607 27 665
  • My work is in the Public Domain for all to share freely.

用中文

  • 读物 书 影片 维基百科

Introduction E9F5FC

Questions FFFFC0

Software

See: Category theory, Yoneda Lemma, Curry-Howard-Lambek

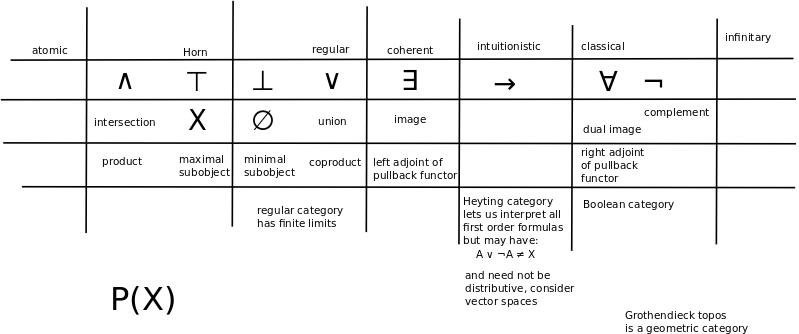
Understand topos theory in terms of regularity of choice.

  • Explore the relation between preorders and presheaves.
  • Think of sets in terms of choice. Compare with lists and with the Axiom of Choice.
  • Understand the graph topos and its subobject classifier.

What is a topos?

  • John Baez.
    • A topos is a category with: A) finite limits and colimits, B) exponentials, C) a subobject classifier.
    • "A topos is category with certain extra properties that make it a lot like the category of sets."
    • "Truth is not a yes-or-no affair: instead, we keep track of "how" true statements are, or more precisely where they are true." Note that how is related to where (scope). This suggests that there are four "hows".
  • A topos is a bridge - the abstract metalevel whose invariants can explain the variety of concrete manifestations at the level.
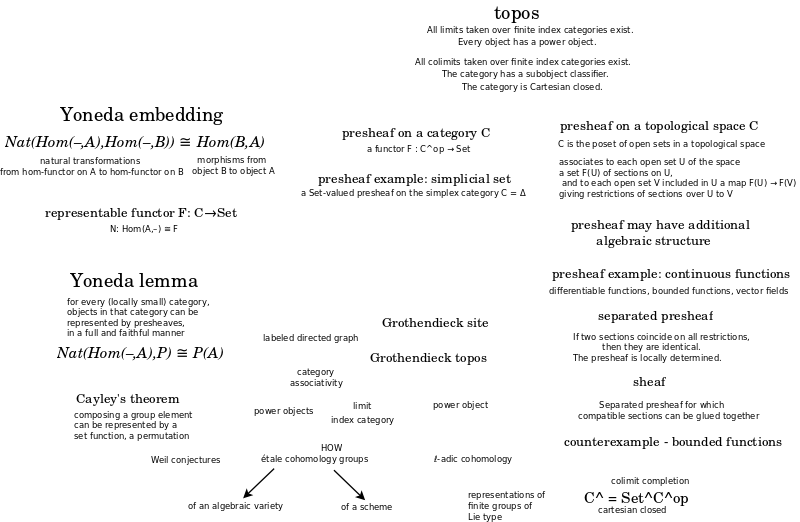
  • A Grothendieck topos is a reflective subcategory of a presheaf category such that the reflection functor preserves finite limits.

A representation of topos is a point of view. (Olivia Caramello, TEDx)

Presheaf category is the total information. Topos is a weakened, limited set of information.

Pullback is crucial because its adjoints are exists and for all.

Pullback (and limits) are the basis for making distinctions.

What are the adjoints for the push forward?

The logic of geometry is based on local coherence. And the global consequences...? are topology?

Morita equivalence.

Double negation in the simpler, topos world, almost holds - but when you translate into the richer world - you get a highly nontrivial statement.

Example: internal view (of complicated curves) are embedded in an external space (and the latter is removed in the topos).

Can define objects and math before logic.

Sheaves are not interesting but rather, what we see from our external point of view, and what needs to be removed to see the interesting internal point of view.

Combinatorics - create objects "for children" - then count them - the formulas appear in other contexts - gives clues for related toposes.

"Sketches of an Elephant: A Topos Theory Compendium 2 Volume Set"

Topos:

  • Category that behaves like the category of sheaves of sets on a site (topological space).
  • Behaves much like the category of sets in that they possess a notion of localization.
  • A generalization of point-set topology.
  • Grothendieck topoi used in algebraic geometry. More general topoi used in logic.

A topos is a category that has the following two properties:

  • All limits taken over finite index categories exist.
  • Every object has a power object.

Grothendieck topos

Let C be a category. A theorem of Giraud states that the following are equivalent:

  • There is a small category D and an inclusion C ↪ Presh(D) that admits a finite-limit-preserving left adjoint.
  • C is the category of sheaves on a Grothendieck site.
  • C satisfies Giraud's axioms, below.

A category with these properties is called a "(Grothendieck) topos". Here Presh(D) denotes the category of contravariant functors from D to the category of sets; such a contravariant functor is frequently called a presheaf.

Giraud's axioms for a category C are:

  • C has a small set of generators, and admits all small colimits. Furthermore, colimits commute with fiber products.
  • Sums in C are disjoint. In other words, the fiber product of X and Y over their sum is the initial object in C.
  • All equivalence relations in C are effective.

The last axiom needs the most explanation. If X is an object of C, an "equivalence relation" R on X is a map R→X×X in C such that for any object Y in C, the induced map Hom(Y,R)→Hom(Y,X)×Hom(Y,X) gives an ordinary equivalence relation on the set Hom(Y,X). Since C has colimits we may form the coequalizer of the two maps R→X; call this X/R. The equivalence relation is "effective" if the canonical map

{$R → X × _{X / R}X$}

is an isomorphism.

Sources

Readings

Videos

Notes

Topos

6 representations

  • Topos theory and subobject classifiers are important to study for describing everything and nothing (classical logic - set theory) and anything and something.
  • Geometry and logic. Truth is in scope: everything (intrinsically, unconditionally true), anything, something, nothing (intrinsically, unconditionally false). Try to define all four scopes in terms of topos theory.

Readings

Colin McLarty: As of the summer of 1973 Grothendieck’s stated preferred definition of topos was still: a category with arbitrary colimits, finite limits, and a small generating set. He says over and over this is not quite adequate for proofs. He says proofs require the notion of site, or else the Giraud axioms, but he calls the vaguer idea more intuitive and says that is the way to think about a topos. [Reminds me of topologies, which have arbitrary unions and finite intersections.]

Edit - Upload - History - Print - Recent changes
Search:
This page was last changed on November 28, 2021, at 10:07 PM