Introduction E9F5FC

Questions FFFFC0

• View
• Edit
• History
• Print

Odd dimensional orthogonal groups reverse orientation. Even dimensional orthogonal groups preserve orientation.

• Even dimensional orthogonal groups are more basic. They model contradiction.
• Even dimensional orthogonal group

In what sense is a triangle of paths different from a triangle of lines.

• A triangle of paths is not oriented. The inside of the triangle is indistinguishable from the outside of the triangle, even in the plane, because the inside of the triangle and the outside of the triangle are one and the same. Whereas a triangle of lines distinguishes the inside and the outside, and so there can be reflections.
• A triangle of lines supports reflection because there can be points on the lines and the lines support a notion of distance.

SO(V) is the special orthogonal group over V.

The odd and even dimensional orthogonal Lie algebras are distinguished by their symmetric form, which pairs their elements, leaving an extra zero in the odd-dimensional case, or not, in the even-dimensional case.

The antipode map on {$\mathbf{R}^p$} sending x to −x has sign {$(-1)^{p}$}, so it is orientation-preserving iff p is even. The orientation character is thus: the non-trivial loop in {$\pi _{1}(\mathbf{RP}^{n})$} acts as {$(-1)^{n+1}$} on orientation, so {$\mathbf{RP}^n$} is orientable iff {$n + 1$} is even, i.e., {$n$} is odd. The projective line {$\mathbf{RP}^1$} is orientable and the projective plane {$\mathbf{RP}^2$} is not orientable. Real projective space

Even dimensional real projective spaces (such as the projective plane) are nonorientable. Odd dimensional real projective spaces (such as the projective line) are orientable.

Projective orthogonal group

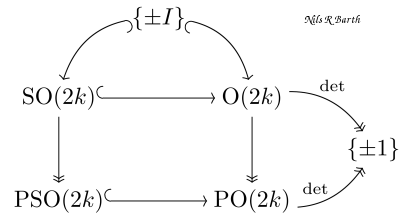
• PO(V) = O(V)/ZO(V) = O(V)/{±I}
• ZSO(V) is the subgroup of orthogonal scalar transformations with unit determinant. Here ZSO is the center of SO, and is trivial in odd dimension, while it equals {±1} in even dimension – this odd/even distinction occurs throughout the structure of the orthogonal groups.
• The structure of the projective orthogonal group differs significantly between odd and even dimension, fundamentally because in even dimension, reflection through the origin is orientation-preserving, while in odd dimension it is orientation-reversing ( {$− I ∈ SO ⁡ ( 2 k )$} but {$− I ∉ SO ⁡ ( 2 k + 1 )$} ). This is seen in the fact that each odd-dimensional real projective space is orientable, while each even-dimensional real projective space of positive dimension is non-orientable. At a more abstract level, the Lie algebras of odd- and even-dimensional projective orthogonal groups form two different families: {$B_k = \mathfrak{s o}_{2 k + 1} , D_k = \mathfrak{s o}_{2 k}$}.
• Thus, {$O ( 2 k + 1 ) = SO ⁡ ( 2 k + 1 ) × { ± I }$}, while {$O ( 2 k ) ≠ SO ⁡ ( 2 k ) × { ± I }$} and is instead a non-trivial central extension of PO(2k).

Idea

• N-spheres where n is even are generated by an odd number of parameters. These spheres are created by suspension, thus have two discrete parts that are separated by the n-1 sphere. Whereas n+1 spheres are generated by an even number of parameters. These spheres are created by rotating the two discrete parts so they coincide.

As a representation of the spin group, this realization of spinors as (complex[j]) column vectors will either be irreducible if the dimension is odd, or it will decompose into a pair of so-called "half-spin" or Weyl representations if the dimension is even.

• The space of spinors is formally defined as the fundamental representation of the Clifford algebra. (This may or may not decompose into irreducible representations.) The space of spinors may also be defined as a spin representation of the orthogonal Lie algebra. These spin representations are also characterized as the finite-dimensional projective representations of the special orthogonal group that do not factor through linear representations.

Andrzej Trautman. Clifford algebras and their representations.

• Relations between orthogonal groups of odd and even dimension: Page 11: Relations between Clifford algebras in spaces of adjacent dimensions. Consider an orthogonal space (V, g) over K and the one-dimensional orthogonal space (K, h1), having a unit vector w ∈ K, h1(w, w) = {$\epsilon$}, where {$\epsilon$} = 1 or −1. The map {$V 3 v 7 → vw ∈ C`0(V ⊕ K, g ⊕ h1)$} satisfies {$(vw)^2 = −\varepsilon g(v, v)$} and extends to the isomorphism of algebras C`(V, −\epsilon g) → C`0(V ⊕ K, g ⊕ h1). This proves (G) There are isomorphisms of algebras: {$C`m → C`0 m+1$} and {$C`k,l → C`0 k+1,l$}.

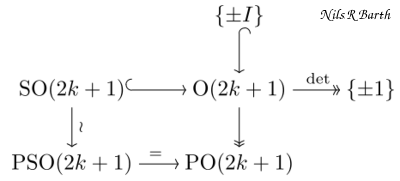
Odd and even

• How are the odd and even dimensional orthogonal groups related to spinors?
• How do odd and even dimensional orthogonal groups distinguish or not the orientation of lines?
• https://en.m.wikipedia.org/wiki/Point_reflection It has determinant {\displaystyle (-1)^{n}}(-1)^{n} (from the representation by a matrix or as a product of reflections). Thus it is orientation-preserving in even dimension, thus an element of the special orthogonal group SO(2n), and it is orientation-reversing in odd dimension, thus not an element of SO(2n + 1) and instead providing a splitting of the map {\displaystyle O(2n+1)\to \pm 1}O(2n+1) \to \pm 1, showing that {\displaystyle O(2n+1)=SO(2n+1)\times \{\pm I\}}{\displaystyle O(2n+1)=SO(2n+1)\times \{\pm I\}} as an internal direct product.
• the Coxeter group {\displaystyle B_{n}}B_{n}. https://en.m.wikipedia.org/wiki/Generalized_permutation_matrix#Signed_permutation_group symmetry group of the hypercube and (dually) of the cross-polytope.
• In addition to preserving length, proper rotations must also preserve orientation. A matrix will preserve or reverse orientation according to whether the determinant of the matrix is positive or negative.
• Pseudoscalar. it is a longest element of the orthogonal group, with respect to the generating set of reflection. It is the longest element of the Coxeter group of signed permutations.
• In SO(2r), reflection through the origin is the farthest point from the identity element with respect to the usual metric. In O(2r + 1), reflection through the origin is not in SO(2r+1) (it is in the non-identity component), and there is no natural sense in which it is a "farther point" than any other point in the non-identity component, but it does provide a base point in the other component.
• Write up proofs of how and which matrices preserve lengths, angles, areas. How do odd and even differ in what they preserve. Volume? Consider symmetries. Consider symmetry spaces.
• Think of affine geometry (with the forgotten origin) as an extra dimension represented by the external gluing point of the odd orthogonal group.
• Dimension of the {$D_n$} is {$2n^2-2n$} as compared to {$2n^2$} for the root systems of {$B_n$} and {$C_n$}.

https://en.wikipedia.org/wiki/Grassmannian

• https://en.wikipedia.org/wiki/Classifying_space
• Grassmannians provide classifying spaces in K-theory, notably the classifying space for U(n). In the homotopy theory of schemes, the Grassmannian plays a similar role for algebraic K-theory.
• The Grassmannian {$G r ( n , R ∞ )$} {\displaystyle Gr(n,\mathbb {R} ^{\infty })} {\displaystyle Gr(n,\mathbb {R} ^{\infty })} of n-planes in R ∞ {\displaystyle \mathbb {R} ^{\infty }} {\displaystyle \mathbb {R} ^{\infty }} is the classifying space of the orthogonal group O(n). The total space is E O ( n ) = V ( n , R ∞ ) {\displaystyle EO(n)=V(n,\mathbb {R} ^{\infty })} {\displaystyle EO(n)=V(n,\mathbb {R} ^{\infty })}, the Stiefel manifold of n-dimensional orthonormal frames in R ∞ . {\displaystyle \mathbb {R} ^{\infty }.}
• Oriented line is the basis for the fiber bundle that gives the Moebius band. Do some orthogonal groups (even or odd) preserve orientation and others not?

What makes even and odd dimensional spheres different?

• https://en.wikipedia.org/wiki/Hairy_ball_theorem holds for even dimensional spheres. The connection with the Euler characteristic χ suggests the correct generalisation: the 2n-sphere has no non-vanishing vector field for n ≥ 1. The difference between even and odd dimensions is that, because the only nonzero Betti numbers of the m-sphere are b0 and bm, their alternating sum χ is 2 for m even, and 0 for m odd.
• https://en.wikipedia.org/wiki/Vector_fields_on_spheres Radon-Hurwitz numbers are related to 8-fold periodicity and to Clifford algebra periodicity
• Balázs Csikós. Vector Fields on Spheres and Clifford Algebras