Introduction E9F5FC

Questions FFFFC0

• View
• Edit
• History
• Print

I am trying to understand Lie groups and algebras because they are central to all of mathematics. Also, it seems that the four classical Lie groups/algebras describe four basic geometries in my diagram of ways of figuring things out.

Lie groups

• Maximal torus describes sets of rotations
• Inner product defines invariants
• Inverses expressed as reversals by way of transposes

Lie algebras

• Distinctive simple roots ground duality of counting forwards and backwards
• Weyl group defines symmetries of choice frameworks and polytopes
• Roots as having inputs and outputs

---

Maximal torus

A compact Lie group has a maximal torus subgroup. A torus is a compact, connected, abelian Lie subgroup and is isomorphic to the standard torus {$T^n$}.

• {$U(n)$} has rank {$n$}. {$T=\{\textrm{diag}(e^{i\theta_1},e^{i\theta_2},...,e^{i\theta_n}\}:\forall j,\theta_j\in\mathbb{R}\}$}
• {$SU(n)$} has rank {$n-1$}. We take the intersection of {$T$} and {$SU(n)$}. {$\sum_{j=1}^{n}\theta_j=0$}
• {$SO(2n)$} has rank {$n$}. A maximal torus consists of matrices with {$2\times 2$} diagonal blocks that are rotation matrices.
• {$SO(2n+1)$} has rank {$n$}. A maximal torus consists of matrices with {$2\times 2$} diagonal blocks that are rotation matrices and with one additional dimension that is fixed.
• {$Sp(n)$} has rank {$n$}. A maximal torus is given by the diagonal matrices whose entries are in a fixed complex subalgebra of {$\mathbb{H}$}.

---

Duality of element and its inverse. Assuring nice inverses

Lie groups are continuous groups. A group involves an inherent duality between an element and its inverse by which every expression has a dual expression in terms of inverses. We can think of the element-inverse duality as an "internal" duality as if one was inverting a shirt from the outside to the inside. Related to this duality is an "external" duality where we can read every expression from left to right or from right to left. This latter duality is external in that it is a duality of form, whereas the internal duality is a duality of content.

A continuous group expresses a continuous duality which can be understood in terms of infinitesimals. This duality is therefore expressed in terms of continuous parameters, thus in terms of divisions rings such as the real numbers, complex numbers, or quaternions. If we restrict ourselves to a finite number of generators, then we can represent the group elements with matrices. Inverses of matrices are given by Cramer's rule. Now, Cramer's rule defines elements in terms of fractions. If we want to deal with integer matrices (why?) then each denominator needs to go away, which means that the matrix must be positive-definite (?) The end result is that the rule for inversion becomes very straightforward, such as transposition (prove). And the issue becomes how to define inversion, how to define that duality... For complex numbers, that duality is intrinsic.

Thinking in pairs of dimensions

It seems that it is all about how to think in pairs of dimensions.

• Dualities express the pairs in all manner of ways.
• The complex numbers are central.
• Rotations occur in two dimensions and relate them.
• Spinors relate two dimensions even more tightly than rotations.
• The matrix {$J$} important for symplectic matrices is just the determinant of the 2 dimensional matrix, the area of a parallelogram: {$a_{11}a_{22} - a_{12}a_{21}$}.
• A pair of real numbers may act like two independent spaces like the split endpoints of {$D_n$}.

Propagating and reflecting a signal for counting

• The simple roots are the ways of propagating a signal, which is to say, of sending it and receiving it. By default, the signal is propagated outward by ever linking to a new node. But the signal can invert itself in three ways: by linking to zero, a mirror which will link to its reflection; by linking directly to its own reflection; or by itself serving as a mirror and linking to the reflection of the previous node. In the latter case, the node is implicitly identified its own reflection but is not explicitly equal to it! (For explicit equality Xn - Xn yields 0.) Thus these cases consider the differences between implicit identification and explicit equality.
• Reflected sequence can't be infinite but must halt. It is counting top-down rather than bottom-up.

Concepts

Bilinear form

• A bilinear form B : V × V → K is called reflexive if B(v, w) = 0 implies B(w, v) = 0 for all v, w in V.
• A bilinear form B is reflexive if and only if it is either symmetric or alternating.

Root systems and polytopes

The hyperplanes of root systems create Weyl chambers and form their edges. Each Weyl chamber is a face of a polytope.

Root system as a pair of spheres

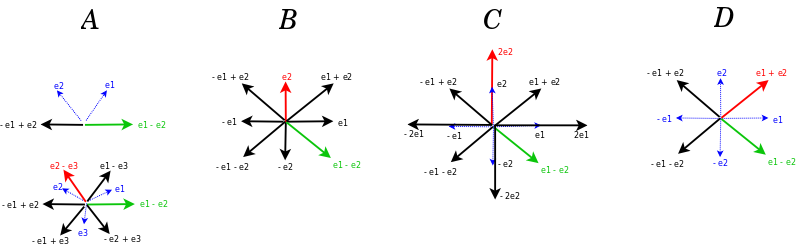
Each of the four classical root systems can be thought of as relating two or three spheres, which is to say, two or three sets of roots {$S_r$}, where the roots in {$S_r$} all have the same length. I distinguish between end roots such as {$\pm e_i$} and {$\pm 2e_i$} and main roots such as {$\pm (e_i \pm e_j)$}. The main roots consist of two spheres of the same radius, Plus and Minus, dictated by the inner sign, which are taken to be the same in the case of {$A_n$} and different otherwise.

• {$A_n$} Plus sphere and Minus sphere are the same (beyond system)
• {$B_n$} end root sphere inside the main root sphere (looking-stepping into system)
• {$C_n$} main root sphere inside the end root sphere (looking-stepping out of system)
• {$D_n$} Plus sphere and Minus sphere are different (within system)

Perhaps we may think of the Plus sphere and Minus sphere having positive and negative radius, accordingly. And perhaps the two spheres are the same in the case of {$A_n$} but distinct otherwise. We may think of {$B_n$} and {$C_n$} as intermediary between same and different. Note that they are looking at opposite directions and so their spheres are inverted. This means that the end root sphere is the system's sphere. Consequently, outide the end root sphere there is no distinction between Plus and Minus and they function completely in parallel. Whereas inside end root sphere they are expressed differently with regard to the end roots.

Note that there is, additionally, a zero sphere.

Similarly, the polytopes can be thought of as generated by trinomials. (I then need to interpret as trinomials the binomials for the simplexes and the coordinate systems.)

Differences between odd and even orthogonal matrices

Conformal orthogonal group Being isometries, real orthogonal transforms preserve angles, and are thus conformal maps, though not all conformal linear transforms are orthogonal. The group of conformal linear maps of Rn is denoted CO(n) for the conformal orthogonal group, and consists of the product of the orthogonal group with the group of dilations. If n is odd, these two subgroups do not intersect, and they are a direct product: CO(2k + 1) = O(2k + 1) × R∗, where R∗ = R∖{0} is the real multiplicative group, while if n is even, these subgroups intersect in ±1, so this is not a direct product, but it is a direct product with the subgroup of dilation by a positive scalar: CO(2k) = O(2k) × R+.

Cayley-Dickson construction for pairs of numbers

• Complex 2 dimensions (dvejybė) leads to quaternions 4 (likimas) and two copies of the reals 1+1 (laisva valia).
• quaternions split the commutativity of the complex numbers

Lie groups and Lie algebras

• Derivative of a curve through the point t=1 is the formulation that links Lie groups and Lie algebras.
• All symmetry groups are subgroups of the orthogonal group.

Symmetric functions of eigenvalues of a matrix

Supposing there is a diagonal matrix whose entries are all distinct, then the subspace of all diagonal matrices is a Cartan subalgebra.

---

The classical Lie groups and Lie algebras: Table of Properties

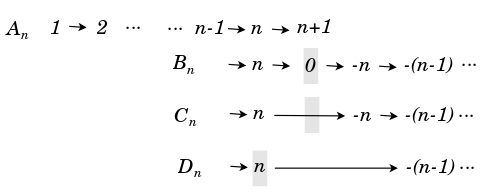
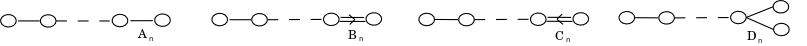
family	{$A_n$}	{$B_n$}	{$C_n$}	{$D_n$}
Lie algebra	{$\mathfrak {sl}_{n+1} $}	{$\mathfrak{so}_{2n+1}$}	{$\mathfrak {sp}_{2n}$}	{$\mathfrak{so}_{2n}$}
dimension	...	odd 2n+1	even 2n	even 2n
Lie algebra	special linear	special orthogonal	symplectic	special orthogonal
nondegenerate bilinear form		symmetric	skew-symmetric	symmetric
constraints on element as matrix A	vanishing trace	skew-symmetric {$-A=A^{T}$}	{$-A=\Omega^{-1}A^\mathrm{T} \Omega$}	skew-symmetric {$-A=A^{T}$}
intrinsic definition		sums of simple bivectors (2-blades) v ∧ w		sums of simple bivectors (2-blades) v ∧ w
symmetric function of eigenvalues	{$w_{1}+...+w_{n}=0$}
Cartan subalgebra	{$h_{1},h_{2}...h_{n-1},$}	{$h_{1}...h_{n},0,$}	{$h_{1}...h_{n},$}	{$h_{1}...h_{n},$}
diagonal entries	{$-h_{1}-h_{2}-...-h_{n-1}$}	{$-h_{1},...,-h_{n-1}$}	{$-h_{1},...,-h_{n-1}$}	{$-h_{1},...,-h_{n-1}$}
constraint from matrix		i≠j		i≠j
root length	all equal	one root shorter than the rest	one root longer than the rest	all equal
nth simple root given simple roots {$x_{i}-x_{j}$}	{$x_{n}-x_{n+1}$}	{$x_{n}-0$}	{$x_{n}--x_{n}$}	{$x_{n}--x_{n-1}$}
roots beyond {$\pm (x_i-x_j)$}		{$\pm (x_i+x_j), \pm x_i$}	{$\pm (x_i+x_j), \pm 2x_i$}	{$\pm (x_i+x_j), i\neq j$}
sequence of basis elements	{$x_{1},\dots,x_{n},x_{n+1},\dots$}	{$\dots,x_{n},0,-x_{n},\dots$}	{$\dots,x_{n},-x_{n},\dots$}	{$\dots,x_{n-1},x_{n},-x_{n-1}\dots$}
duality - a total of 8 dimensions!	two dimensions: forward outside and backward inside	one dimension - outside - collapsed	four dimensions - two sequences	one dimension - inside - collapsed
temporal interpretation	future	absolute	present	past
ultimate node: the bridge to self-duality	new node: no reflection	zero	reflection of same node	reflection of previous node
signal behavior	propagates outward, away from its reflection	links to zero, a mirror which will link to its reflection	links directly to its own reflection	identifies with its own reflection, thus serves as a mirror and links to the reflection of the previous node
distance from its own reflection	≥2	2	1	0
nature of mirror	no mirror	explicit mirror	implicit mirror	self-mirror
Lie group	special unitary SU(n)	special orthogonal SO(2n+1)	symplectic Sp(2n, C)	special orthogonal SO(2n)
group elements as matrices	unitary with determinant 1	orthogonal: columns and rows are orthonormal	symplectic with entries in C	orthogonal: columns and rows are orthonormal
inverse matrix equals	conjugate transpose	transpose	quaternionic transpose	transpose
group preserves	volume and orientation in {$\mathbb{R}^{n}$}	distance and a fixed point	oriented area?	distance and a fixed point
related group preserves inner product	U(n): complex	O(n):real	Sp(n):quaternionic	O(n):real
generalization of group preserves nondegenerate bilinear form or quadratic form	-	symmetric	skew-symmetric	symmetric
Weyl group / Coxeter group	symmetric group	hyperoctahedral group	hyperoctahedral group	subgroup of index 2 of the hyperoctahedral group

---

Cartan matrix

The Cartan matrix is determined by the inner product as shown below. It gives the number of times one root my be added to another root and stay within the root system. Thus it is a measure of slack or freedom. This means that {$G_{2}$} measures a three fold slack of the kind needed for the operations +1, +2 and +3 on the eight-cycle of divisions of everything.

{$a_{ij}= \frac{2(r_{i},r_{j})}{(r_{i},r_{i})}$}

H, X and Y are determined by Serre's relations.

Lie family

Cartan matrix

{$H_{i}$}

{$X_{i}$}

{$Y_{i}$}

---

{$A_{n} \begin{bmatrix} \ddots & & \\ & 2 & -1 \\ & -1 & 2 \end{bmatrix}$}

{$\begin{pmatrix} \ddots & & \\ & 1 & \\ & & -1 \end{pmatrix}$} {$\begin{pmatrix} \ddots & & \\ & 0 & 1\\ & & 0 \end{pmatrix}$} {$\begin{pmatrix} \ddots & & \\ & 0 & \\ & 1 & 0 \end{pmatrix}$}

---

{$B_{n} \begin{bmatrix} \ddots & & \\ & 2 & -2 \\ & -1 & 2 \end{bmatrix}$}

Almost all of the simple roots look like this... And they generate a first set of roots (as with the {$A_{n}$} family).

{$\begin{pmatrix} 1 & & & & \\ & -1 & & & \\ & & \ddots & & \\ & & & {\color{Red} 1} & \\ & & & & {\color{Red}{-1}} \end{pmatrix}$} {$\begin{pmatrix} 0 & 1 & & & \\ & 0 & & & \\ & & \ddots & & \\ & & & 0 & {\color{Red}{-1}}\\ & & & & 0 \end{pmatrix}$} {$\begin{pmatrix} 0 & & & & \\1 & 0 & & & \\ & & \ddots & & \\ & & & 0 & \\ & & & {\color{Red}{-1}} & 0 \end{pmatrix}$}

And there is one more below. (What type of interference will you have if you count forwards and backwards at the same time? Here they superimpose to give 0.)

{$\begin{pmatrix} 0 & & & & \\ & 1 & & & \\ & & -1 + {\color{Red}{1}} & & \\ & & & {\color{Red}{-1}} & \\ & & & & 0 \end{pmatrix}$} {$\begin{pmatrix} 0 & & & & \\ & 0 & 1 & & \\ & & 0 & {\color{Red}{-1}} & \\ & & & 0 & \\ & & & & 0 \end{pmatrix}$} {$\begin{pmatrix} 0 & & & & \\ & 0 & & & \\ & 1 & 0 & & \\ & & {\color{Red}{-1}} & 0 & \\ & & & & 0 \end{pmatrix}$}

And together this generates a second set of roots (in the other quadrants) which look like this...

{$\begin{pmatrix} 1 & & & & \\ & {\color{Red}{1}} & & & \\ & & \ddots & & \\ & & & -1 & \\ & & & & {\color{Red}{-1}} \end{pmatrix}$} {$\begin{pmatrix} & & & 1 & 0 \\ & & & 0 & {\color{Red}{-1}} \\ & & 0 & & \\ & 0 & & & \\ 0 & & & & \end{pmatrix}$} {$\begin{pmatrix} & & & & 0 \\ & & & 0 & \\ & & 0 & & \\ 1 & 0 & & & \\ 0 & {\color{Red}{-1}} & & & \end{pmatrix}$}

---

{$C_{n} \begin{bmatrix} \ddots & & \\ & 2 & -1 \\ & -2 & 2 \end{bmatrix}$}

{$\begin{pmatrix} 1 & & & & \\ & -1 & & & \\ & & \ddots & & \\ & & & {\color{Red} 1} & \\ & & & & {\color{Red}{-1}} \end{pmatrix}$} {$\begin{pmatrix} 0 & 1 & & & \\ & 0 & & & \\ & & \ddots & & \\ & & & 0 & {\color{Red}{-1}}\\ & & & & 0 \end{pmatrix}$} {$\begin{pmatrix} 0 & & & & \\1 & 0 & & & \\ & & \ddots & & \\ & & & 0 & \\ & & & {\color{Red}{-1}} & 0 \end{pmatrix}$}

Here they superimpose to give a mixed state {$\pm 1$}.

{$\begin{pmatrix} \ddots & & & \\ & 1 & & \\ & & -1 & \\ & & & \ddots \end{pmatrix}$} {$\begin{pmatrix} \ddots & & & \\ & 0 & \pm 1 & \\ & & 0 & \\ & & & \ddots \end{pmatrix}$} {$\begin{pmatrix} \ddots & & & \\ & 0 & & \\ & \pm 1 & 0 & \\ & & & \ddots \end{pmatrix}$}

The second set of roots look like this:

{$\begin{pmatrix} 1 & & & & \\ & {\color{Red}{1}} & & & \\ & & \ddots & & \\ & & & -1 & \\ & & & & {\color{Red}{-1}} \end{pmatrix}$} {$\begin{pmatrix} & & & \pm 1 & 0 \\ & & & 0 & {\color{Red}{\pm 1}} \\ & & 0 & & \\ & 0 & & & \\ 0 & & & & \end{pmatrix}$} {$\begin{pmatrix} & & & & 0 \\ & & & 0 & \\ & & 0 & & \\ \pm 1 & 0 & & & \\ 0 & {\color{Red}{\pm 1}} & & & \end{pmatrix}$}

---

{$D_{n} \begin{bmatrix} \ddots & & & \\ & 2 & & -1 \\ & & 2 & -1 \\ & -1 & -1 & 2 \end{bmatrix}$}

The usual simple roots, which generate the first set of roots:

{$\begin{pmatrix} 1 & & & & \\ & -1 & & & \\ & & \ddots & & \\ & & & {\color{Red} 1} & \\ & & & & {\color{Red}{-1}} \end{pmatrix}$} {$\begin{pmatrix} 0 & 1 & & & \\ & 0 & & & \\ & & \ddots & & \\ & & & 0 & {\color{Red}{-1}}\\ & & & & 0 \end{pmatrix}$} {$\begin{pmatrix} 0 & & & & \\1 & 0 & & & \\ & & \ddots & & \\ & & & 0 & \\ & & & {\color{Red}{-1}} & 0 \end{pmatrix}$}

The additional root is simply a member of the second set of roots.

{$\begin{pmatrix} \ddots & & & & & \\ & 1 & & & & \\ & & {\color{Red}{1}} & & & \\ & & & -1 & & \\ & & & & {\color{Red}{-1}} & \\ & & & & & \ddots \end{pmatrix}$} {$\begin{pmatrix} \ddots & & & & & \\ & 0 & & 1 & & \\ & & 0 & & {\color{Red}{-1}} & \\ & & & 0 & & \\ & & & & 0 & \\ & & & & & \ddots \end{pmatrix}$} {$\begin{pmatrix} \ddots & & & & & \\ & 0 & & & & \\ & & 0 & & & \\ & 1 & & 0 & & \\ & & {\color{Red}{-1}} & & 0 & \\ & & & & & \ddots \end{pmatrix}$}

Together they generate a second set of roots (in the other quadrants) which look like this...

{$\begin{pmatrix} 1 & & & & \\ & {\color{Red}{1}} & & & \\ & & \ddots & & \\ & & & -1 & \\ & & & & {\color{Red}{-1}} \end{pmatrix}$} {$\begin{pmatrix} & & & 1 & 0 \\ & & & 0 & {\color{Red}{-1}} \\ & & & & \\ & 0 & & & \\ 0 & & & & \end{pmatrix}$} {$\begin{pmatrix} & & & & 0 \\ & & & 0 & \\ & & & & \\ 1 & 0 & & & \\ 0 & {\color{Red}{-1}} & & & \end{pmatrix}$}

---

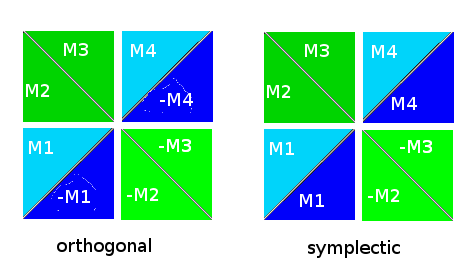
A' is the transpose of A across the anti-diagonal.

---

{$\mathfrak{sl}(n+1, \mathbb{C})$}

{$ \begin{pmatrix} h_{1}, h_{2}, \dots, h_{n} \end{pmatrix}$}

matrices whose trace is zero.

---

{$\mathfrak{so}(2n+1, \mathbb{C}) $}

{$ \begin{pmatrix} h_{1}, \dots, h_{n}, 0, -h_{n}, \dots, -h_{1} \end{pmatrix}$}

{$\begin{pmatrix} \begin{pmatrix} a_{11} & a_{1n} \\ a_{n1} & a_{nn} \end{pmatrix} & V & \begin{pmatrix} B & 0 \\ 0 & -B' \end{pmatrix} \\ W & 0 & -V' \\ \begin{pmatrix} C & 0 \\ 0 & -C' \end{pmatrix} & -W' & \begin{pmatrix} -a_{nn} & -a_{1n} \\ -a_{n1} & -a_{11} \end{pmatrix} \end{pmatrix}$}

---

{$\mathfrak{sp}(n, \mathbb{C})$}

{$ \begin{pmatrix} h_{1}, \dots, h_{n}, -h_{n}, \dots, -h_{1} \end{pmatrix}$}

{$ \begin{pmatrix} \begin{pmatrix} a_{11} & a_{1n} \\ a_{n1} & a_{nn} \end{pmatrix} & \begin{pmatrix} B & 0 \\ 0 & B' \end{pmatrix} \\ \begin{pmatrix} C & 0 \\ 0 & C' \end{pmatrix} & \begin{pmatrix} -a_{nn} & -a_{1n} \\ -a_{n1} & -a_{11} \end{pmatrix} \end{pmatrix}$}

---

{$\mathfrak{so}(2n, \mathbb{C})$}

{$ \begin{pmatrix} h_{1}, \dots, h_{n}, -h_{n}, \dots, -h_{1} \end{pmatrix}$}

{$ \begin{pmatrix} \begin{pmatrix} a_{11} & a_{1n} \\ a_{n1} & a_{nn} \end{pmatrix} & \begin{pmatrix} B & 0 \\ 0 & -B' \end{pmatrix} \\ \begin{pmatrix} C & 0 \\ 0 & -C' \end{pmatrix} & \begin{pmatrix} -a_{nn} & -a_{1n} \\ -a_{n1} & -a_{11} \end{pmatrix} \end{pmatrix}$}

---

{$J = \begin{bmatrix} 0 & I_n \\ - I_n & 0\end{bmatrix}$}

Compact Lie groups

• {$SU(n+1) = \{ A \in M_{n+1}(\mathbb{C}) | {\overline{A}}^T A = I, \operatorname{det}(A) = 1 \}$}
• {$SO(2n+1) = \{ A \in M_{2n+1}(\mathbb{R}) | A^T A = I, \operatorname{det}(A) = 1 \}$}
• {$Sp(n) = \{ A \in U(2n) | A^T J A = J \}$}
• {$SO(2n) = \{ A \in M_{2n}(\mathbb{R}) | A^T A = I, \operatorname{det}(A) = 1 \}$}||

Complexification of associated Lie algebra

• {$\mathfrak{sl}(n+1, \mathbb{C}) = \{ X \in M_{n+1}(\mathbb{C}) | \operatorname{tr} X = 0 \}$}
• {$\mathfrak{so}(2n+1, \mathbb{C}) = \{ X \in M_{2n+1}(\mathbb{C}) | X^T + X = 0 \}$}
• {$\mathfrak{sp}(n, \mathbb{C}) = \{ X \in M_{2n}(\mathbb{C}) | X^T J + JX = 0 \}$}
• {$\mathfrak{so}(2n, \mathbb{C}) = \{ X \in M_{2n}(\mathbb{C}) | X^T + X = 0 \}$}

Building a Lie group from a Lie algebra

General linear

Special linear

• Det (1 + εX) = 1 + ε Trace(X) so Det=1 when Trace=0
• Det 1 preserve a volume form
• Trace 0 is like Divergence 0 for vector fields.

Orthogonal

• preserves lengths
• {$g^(T)Bg = B$}
• {$(I + εx)^(T)B(I+εx) = B$}
• {$B + ε(x^(T)B+Bx) = B$}
• so {$x^(T)B+Bx=0$}

Symplectic

---

Literature

• Classical Groups by Kevin McGerty discusses them as composition algebras.
• Geometry of Classical Groups over Finite Fields and Its Applications, Zhe-xian Wan
• Atiyah-Bott-Shapiro (1963) theorem about Clifford algebras of {$\mathbb{R}_{n}$}.
• Chevalley basis
• Semisimple Lie algebra
• Serre's theorem on a semisimple Lie algebra Serre's relations
• Lie group decomposition

Video

• Hermitian K-theory by Karoubi is an analogue to Lie classical groups - orthogonal, unitary, symplectic - and perhaps a unification of them. See Karoubi's video 32:00 on Quadratic forms and Bott periodicity.