- MathNotebook
- MathConcepts
- StudyMath
- Geometry
- Logic
- Bott periodicity
- CategoryTheory
- FieldWithOneElement
- MathDiscovery
- Math Connections
Epistemology
- m a t h 4 w i s d o m - g m a i l
- +370 607 27 665
- My work is in the Public Domain for all to share freely.
- 读物 书 影片 维基百科
Introduction E9F5FC
Questions FFFFC0
Software
See: Math notebook, Classical Lie groups, Classical Lie Root systems?, Intuiting exceptional root systems
Intuit the four classical root systems.
The four classical root systems are as follows, where throughout, {$i>j$}:
| {$A_n$} | {$\pm (x_i-x_j)$} |
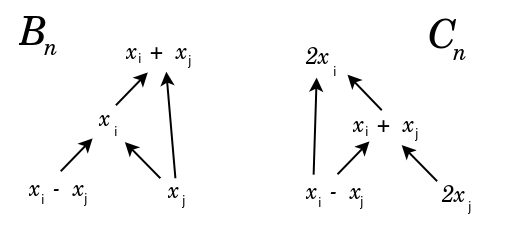
| {$B_n$} | {$\pm (x_i-x_j), \pm (x_i+x_j), \pm x_i$} |
| {$C_n$} | {$\pm (x_i-x_j), \pm (x_i+x_j), \pm 2x_i$} |
| {$D_n$} | {$\pm (x_i-x_j), \pm (x_i+x_j)$} |
We thus see that all classical root systems contain the roots {$\pm (x_i-x_j)$}.
{$C_n$} includes the case {$i=j$}. {$B_n$} and {$D_n$} do not. But {$B_n$} fakes it by having a zero. This yields the same lattice as {$C_n$}. But the root systems bring out the difference. So {$C_n$} gives the conditions needed for this identity. The root systems are building up the context for such an identity.
In particular, {$B_n$}, {$C_n$}, {$D_n$} have two conjugate sets of roots because they are establishing the symmetries underlying a pair of expansions linked by a comparison, an identity. Thus we have a value on the left which is being compared to a value on the right. In the case of {$C_n$} we may have identity, an equal sign. In the case of {$B_n$} we may have a zero. In the case of {$D_n$} we have neither.
The Dynkin diagram for {$D_2$} is a pair of dots. This brings to mind the two conjugate roots of -1. Thus there is this inherent symmetry within {$D_n$}.
Consider this as a problem of the ways of coding counting. And coding is counted by a minus sign. This codes counting both forwards and backwards. But how might the two directions coincide? There are four possibilities. The second direction can be coded with a plus sign. Then the two can be related in three different ways.
Earlier notes
Counting (in Lie root system) can change to B, C, D only once! That puts a cap on the one end. Then the counting must continue on the other end, extending it. A second cap may not be put on that end. There cannot be a cycle.
Counting (by way of the simple roots) links + and - in a chain. x2-x1 etc.
Chess pieces (rooks, bishops, knights) move in very basic ways that bring to mind root systems and especially the geometries that they open up in the gap they create by being more complex e_i - e_j than the generic basis e_i.
Lie algebras (root systems) are the cracks or gaps between coordinate system layers. The "higher energy" a system has, the bigger the crack, the more possibility for variation and freedom, how the system will develop or degenerate. The lowest energy system is the one that has the roots e_i (and its byproducts, e_i-e_j, e_i+e_j etc.) because everything is explicit. And the highest energy system is A_n, given by e_i-e_j, because the e_i are implicitly latent.
The root systems, as a minimum, have to contain the e_i - e_j because they encode the Lie bracket of the e_i. The question is, what are the ways that they can be expanded? First, a dual encoding can be given e_i + e_j. And the two must then be related in one of the various ways.
