Introduction E9F5FC

Questions FFFFC0

• View
• Edit
• History
• Print

Binomial Bott, Polytopes, Classical Lie Groups, Representation theory

二项式定理

Why, intuitively, are there 4 classical Lie groups/algebras?

I am deriving the answer from the 4 different kinds of symmetries inherent in choice. These yield the following four interpretations of the binomial theorem in terms of polytopes:

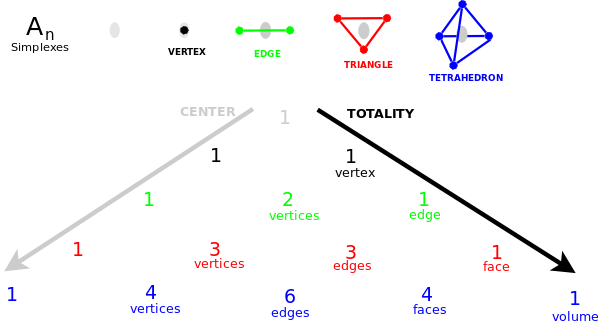
• {$ \prod_{i}(\varnothing + \leftrightarrow_{i}) $} Simplexes.
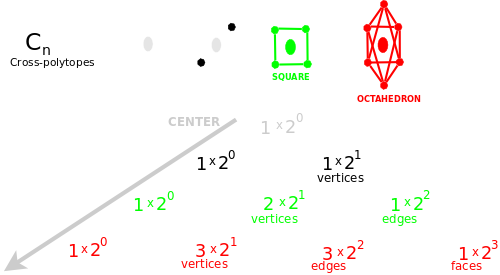
• {$ \prod_{i}(\varnothing + (\leftarrow_{i} + \rightarrow_{i})) $} Cross-polytopes.
• {$ \prod_{i}((\leftarrow_{i} + \rightarrow_{i})+\leftrightarrow_{i}) $} Cubes.
• {$ \prod_{i}(\leftarrow_{i} + \rightarrow_{i}) $} Cube slices.

Note that swapping {$\leftarrow_{i}$} and {$\rightarrow_{i}$} maps {$\leftrightarrow_{i}$} to itself. This is why the Weyl group has order {$2^n n!$} and not, say, {$3^n n!$}. Thus {$\leftrightarrow_{i}$} is similar to {$\varnothing$} but it behaves as a pseudocenter (much like a pseudoscalar, the highest grade element in a Clifford algebra). A whole is a pseudocenter in that it is only defined with regard to a set of known dimensions whereas a center is defined with regard to all possible dimensions. The known dimensions are the ones which an index runs over.

How to relate (-n,...,-2,-1) with (1,2,...,n)? along the diagonal of a matrix (the Cartan subalgebra). So that they maintain a duality. What are the ways of supporting the duality in a counting process?

I need to relate these to the ways of linking up two sequences. Linking ...XYZ and ...ABC can have the following solutions:

• XYZABC (folding)
• XYZ0ABC (linking externally - odd!)
• XY0BC where 0=Z=A (linking internally - even!)

and this lastmost statement is an equivalence, thus this is a context for defining equivalence.

Dorovės atžvilgiu, tai susitarimo galimybės. Vidinės ir išorinės?

In geometry, rotating by 90 degrees makes for independence. So the root systems impose this on the algebra.

If I make three choices, then a fourth choice "left" makes a difference; whereas a fourth choice of not choosing makes no difference - the center of a triangle stays the same no matter how many dimensions you add.

Interpret (A-B)^N.

Conjugacy classes counted by expanding multinomial theorem where certain letters (choices) are set the same.

Lie algebra linking - is given by placing a cube on its corner and projecting its vertices onto the plane, yielding A2.

Note that ← and → add to yield paths. They are within the same system. Whereas \ast and \ast are in different systems.

Crucial fact is its about the inherent geometry in sequential choices. (Choices made one-by-one as opposed to being made all at once.)

Extrinsic vs. intrinsic.

Slack lets you turn around.

• Coordinate system - broken up relations, qualities (counting vertices) - existence is internal - dimensions are not ordered - commutative.
• Simplex - existence is external - relations of things with regard to each other (counting subsets)(ordered choices, vertices) - noncommutative.

A coordinate system (sliced cube) has each vertex face in two directions (left and right). But in a simplex the vertices face in only one direction (outside not inside). (Compare with hyperoctahedral group in terms of shuffling cards with two sides.)

Explicit choice "thing" vs. "no-thing" ("choose" vs. "don't choice") choices yield a syntactically asymmetric outcome "everything" vs. "nothing", whereas implicit choice "this" vs. "that" yields a syntactically symmetric outcome. (all "this" and all "that" is the same).

Commutative or noncommutative?

The choice itself is different ... or what is chosen (this or that)?

Observer and observed. An observer waits for the answer. The observed doesn't wait - it has no concept.

Entropy. Reversibility of time (intrinsic geometry) vs. asymmetry of time (extrinsic geometry). Grace requires "extra" states. With justice there are no extra states.

Note that the infinite paths down Pascal's triangle correspond to the real numbers from 0 to 1 in base 2.

How is Pascal's cone - the circular row - related to a finite field? and how it changes with q?

Cube slices have an externally referent system - so when you flip it - you flip the coordinate axes as well - keeping it symmetric. Simplexes have a self-referent system so if you flip it, then you get...?

Walks on trees - binomial theorem

Differentiation (body + edge)^N or (long+short)^N

(left + right) is a repeated experiment, a repeated choice - left is consistent, right is consistent, in each choice - this is needed for doing measurements and experiments

Is it closing a cycle? Or is it turning counting around, as when facing God and turning around to view with him?

Counting Young diagrams: Having empty outer column vs. having nonempty bottom row. How does the q-analogue work?

Indistinguishable boson and distinguishable fermion.

Write up: Conjugation is relabeling.

Dimensions of counting

• Simplex-complex numbers (2 disconnected dimensions)
• Cross-polytopes - reals (1 linked dimension)
• Cubes - reals (1 linked dimension)
• Symplexes - quaternions (4 folded, disconnected dimensions)

Projective linked by adding an extra point - infinity. Affine - internal zero - what would that mean?

{$ (∅ + \ast)^n $} Simplexes.

• The number of ways to choose k elements from an n-element set.
• The subsimplexes of a simplex.

{$ (∅ + (← + →))^n $} Cross-polytopes.

• Trinomial expansion

{$ ((← + →)+ \ast)^n $} Cubes.

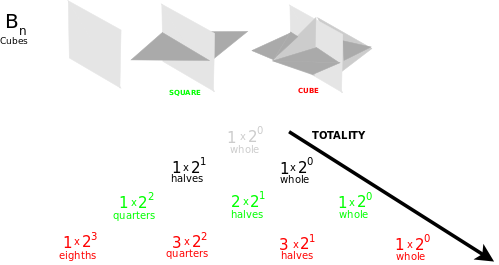
• {$ (SHORT + LONG + \ast)^n $} Dividing up a cube.
• {$ (BODY + EDGE + \ast)^n $} Differentiating the volume of a cube.

{$ (← + →)^n $} Cube slices.

Sources

• Notes on the combinatorial fundamentals of algebra. Darij Grinberg.
• Wikipedia: Binomial theorem
  • Newton's generalized binomial theorem - allow noninteger exponents
  • Multiple angle identities and De Moivre's formula
  • Definition of e as expansion of {$ (1 + 1/n)^n $}
• Pascal's triangle
  • Fourier transform of sin(x)n+1/x
• Binomial coefficient
• Wikipedia: Binomial series
• General Leibniz rule for nth derivative of a product
• Binomial distribution
• Negative binomial distribution
• Alternativity suffices in place of associativity
• Gamma function
• Gaussian binomial coefficient
• Trinomial expansion, Pascal's pyramid
• Inclusion-exclusion principle
• Grassmanian
• Euler characteristic 0 = 1 - V + E - F + 1
• Gauss Bonet theorem relates curvature to Euler characteristic. It is generalized by generalized Gauss-Bonnet theorem, Chern-Weil homomorphism, Riemann-Roch theorem, Atiyah-Singer theorem.
• Betti numbers, Poincare polynomial
• homology.
• Geometric representation theory
• Young tableaux (conceived as paths in Pascal's triangle)

Related

• Bell triangle ways of partitioning a finite set into subsets
• Fibonacci polynomials can be read off of Pascal's triangle.
• Hypergeometric function

See also

• Eulerian number
• Schur polynomial
• Macdonald polynomials

Q-analogues

• Young diagrams

M M* = 1 This gives a structural, geometric interpretation for an involution - there is natural symmetry in the form of a matrix - like the root systems - and the point of having orthogonality, orthonormality - a set of combinatorially nice, independent basis elements to work with

• e to the matrix consisting of the natural numbers on its first off-diagonal gives a triangular matrix with pascal's triangle. and how is it in the case of the cube?
• Pascal's triangle tilted gives Fibonacci numbers
• I dreamed of the binomial theorem as having an "internal view", imagined from the inside, which accorded with the "coordinate systems". And which interweaved with the external views to yield various "moments", given by curves on the plane, variously adjusted and transformed by the internal view.