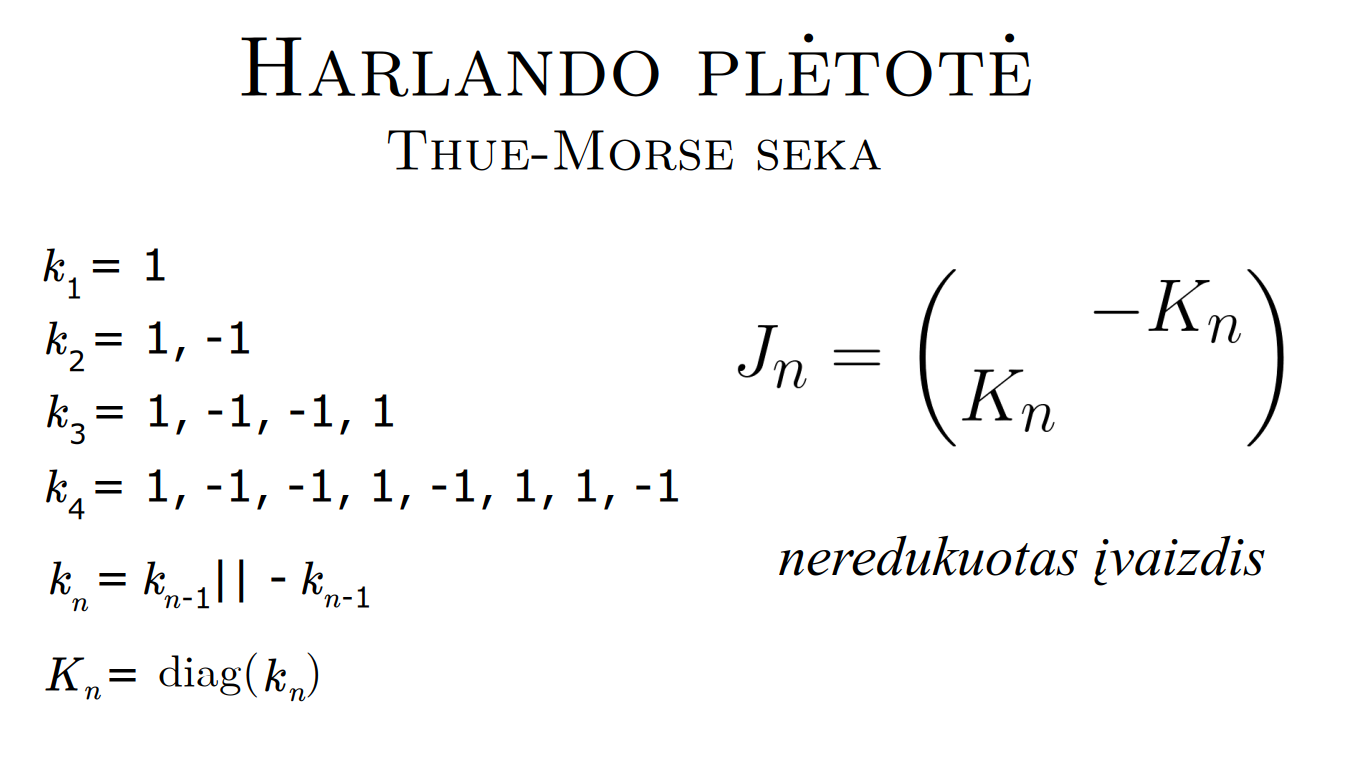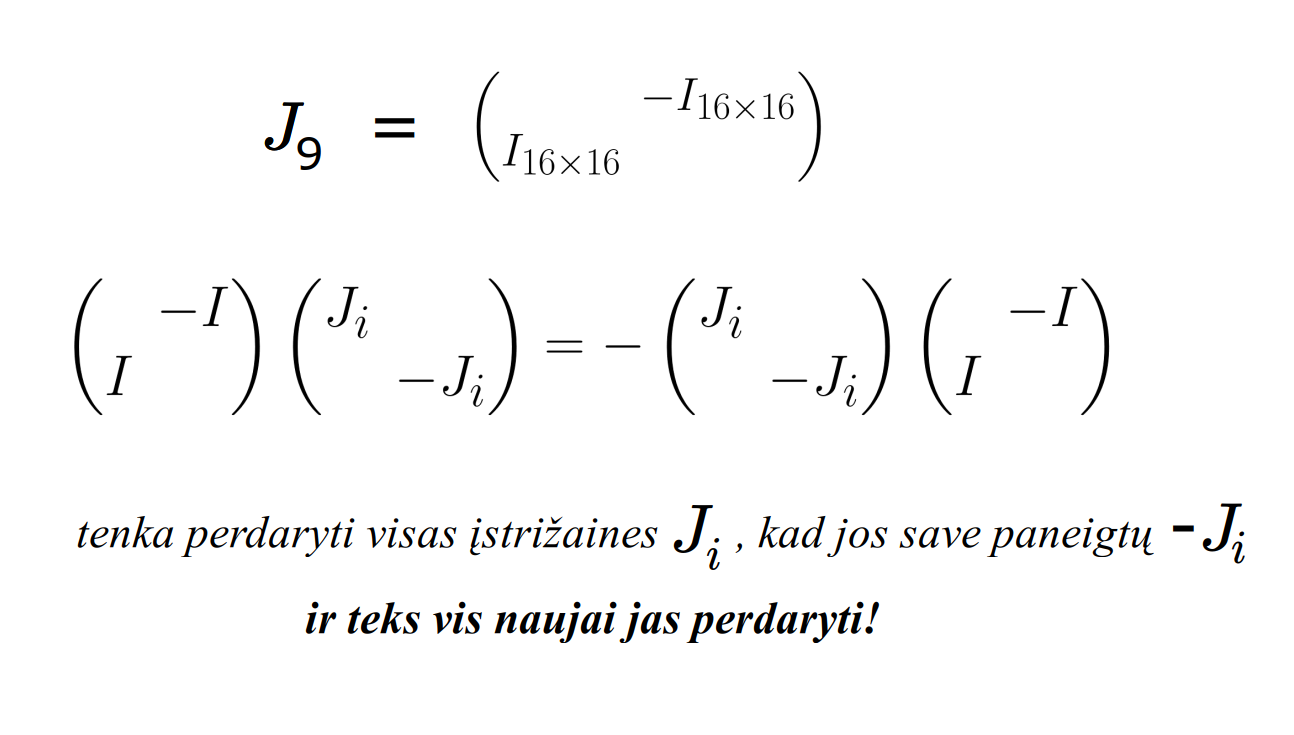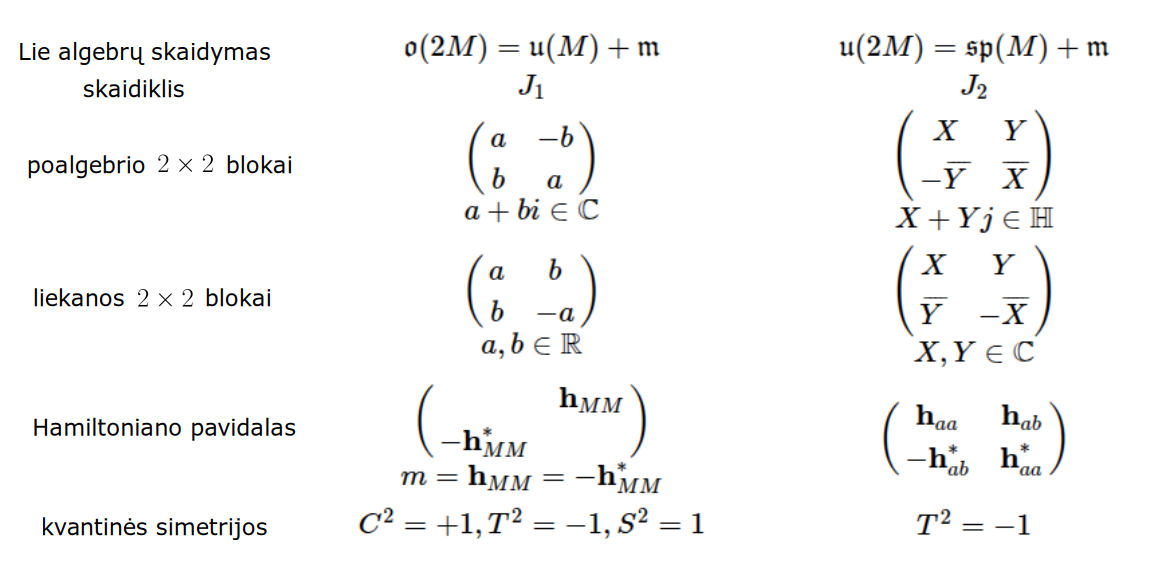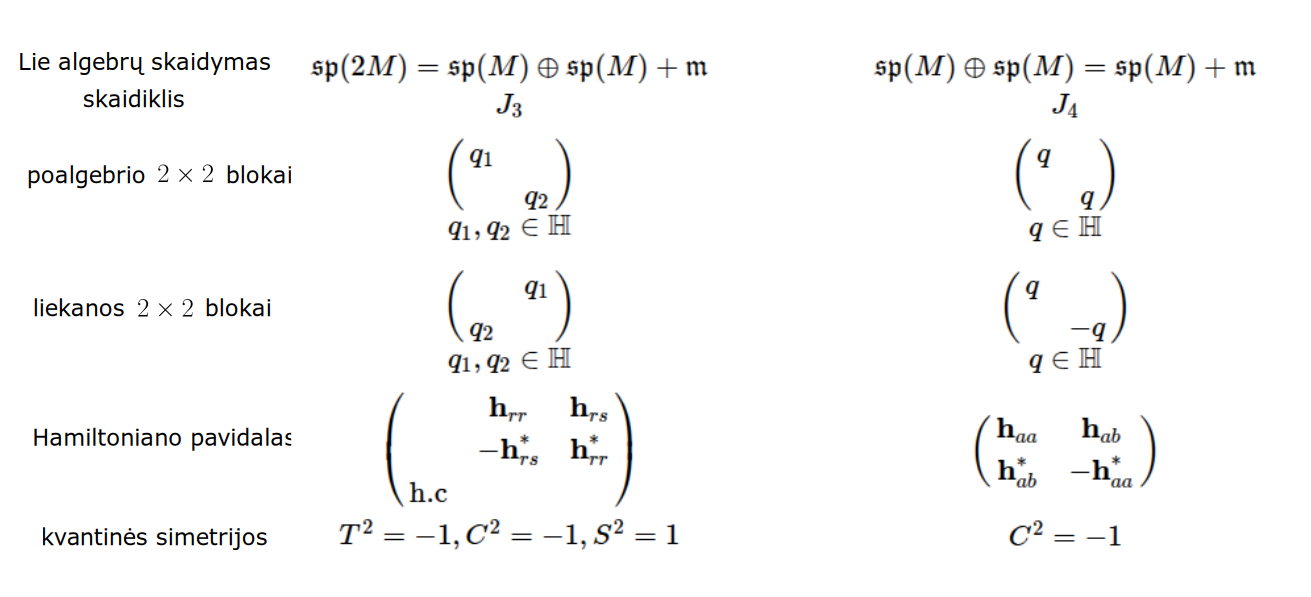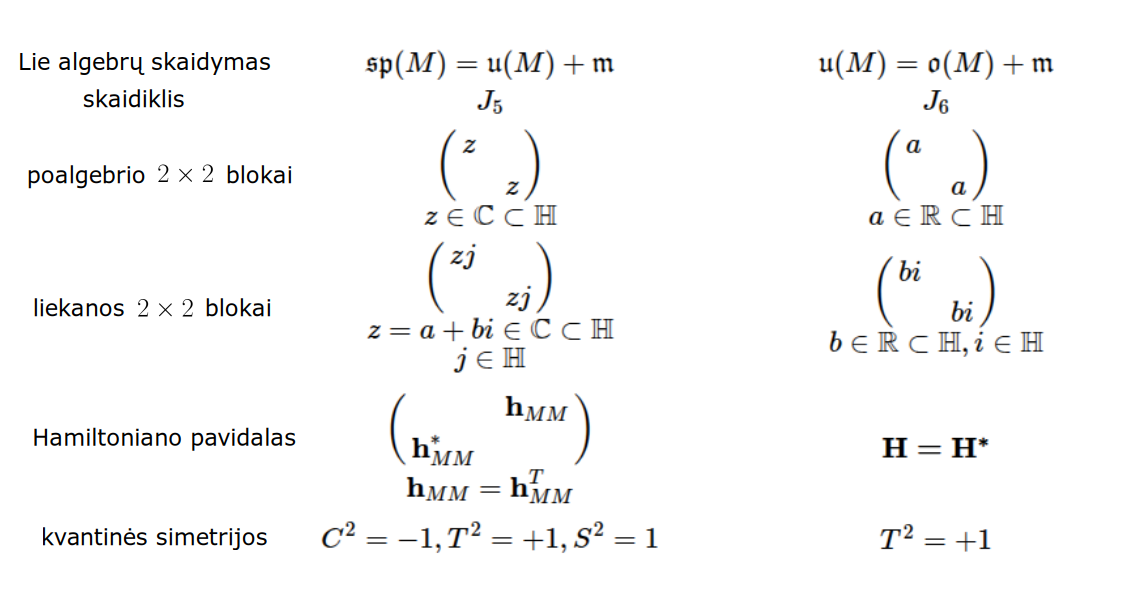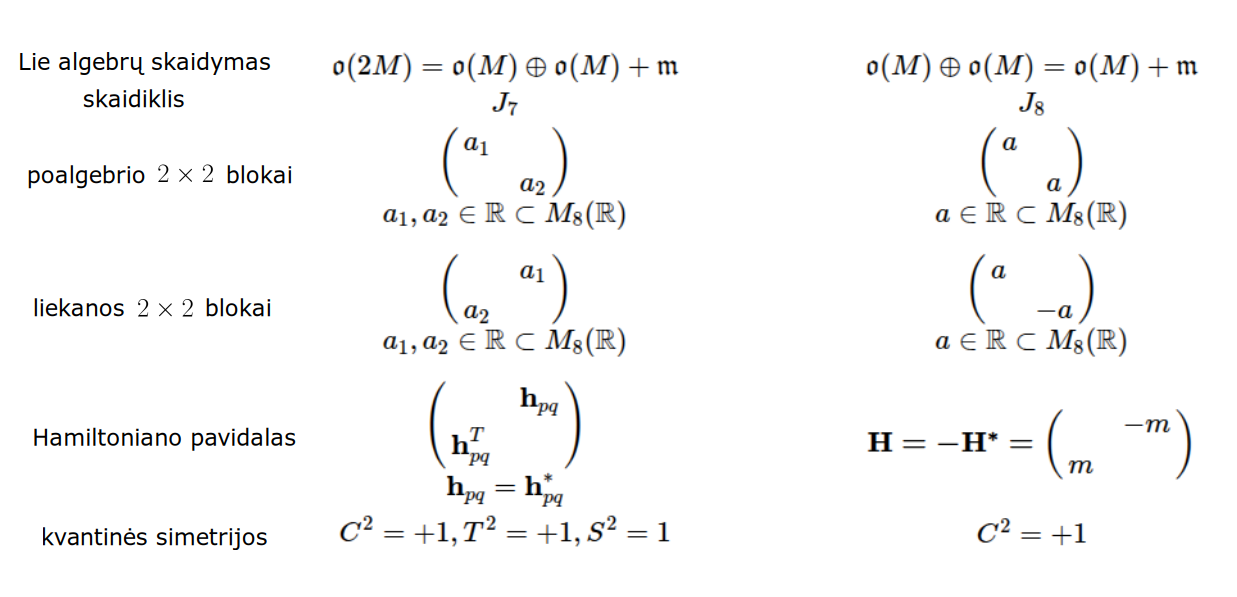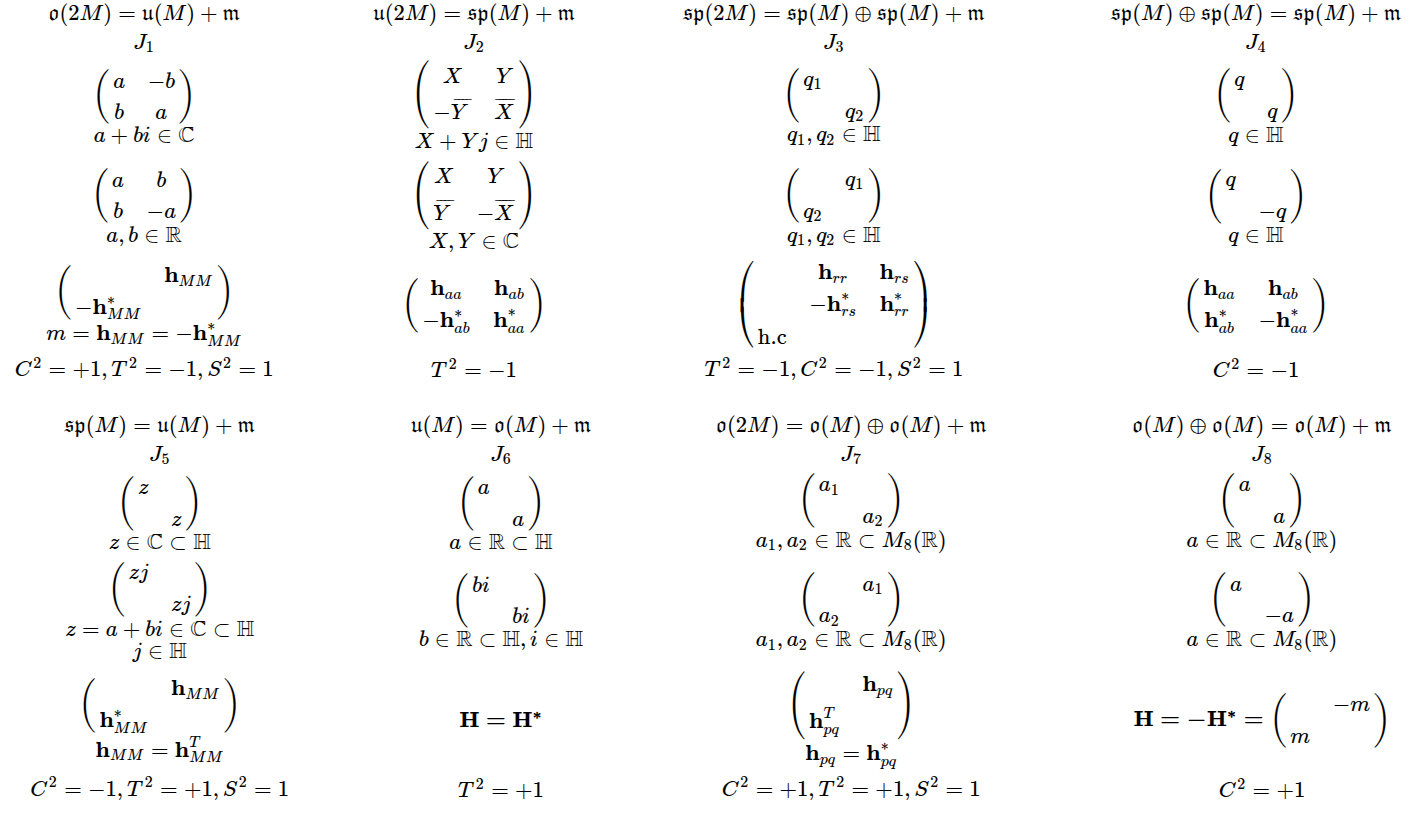Math 4 Wisdom. "Mathematics for Wisdom" by Andrius Kulikauskas.

Bott periodicity, VGTU žemėlapis, skaidrės, 2025 m. spalio 28 d., 9:00 val. S6 (SRL-I) 401

An Allegory: The Solipsistic Self as the Hamiltonian of a Noninteracting Fermion

Savasties būsenų modeliavimas hamiltoniano 3 kvantinėmis simetrijomis bei Bott periodiškumu

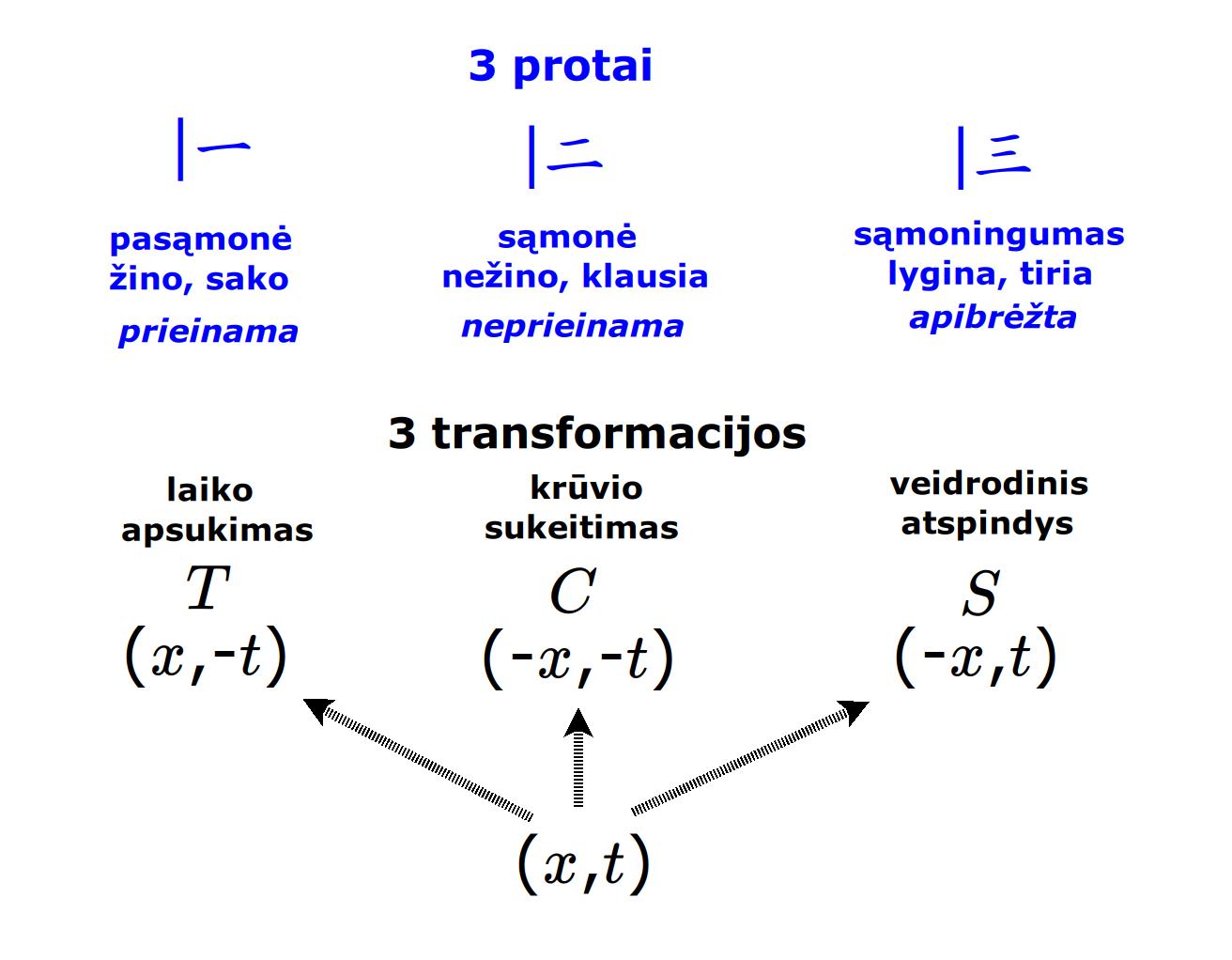
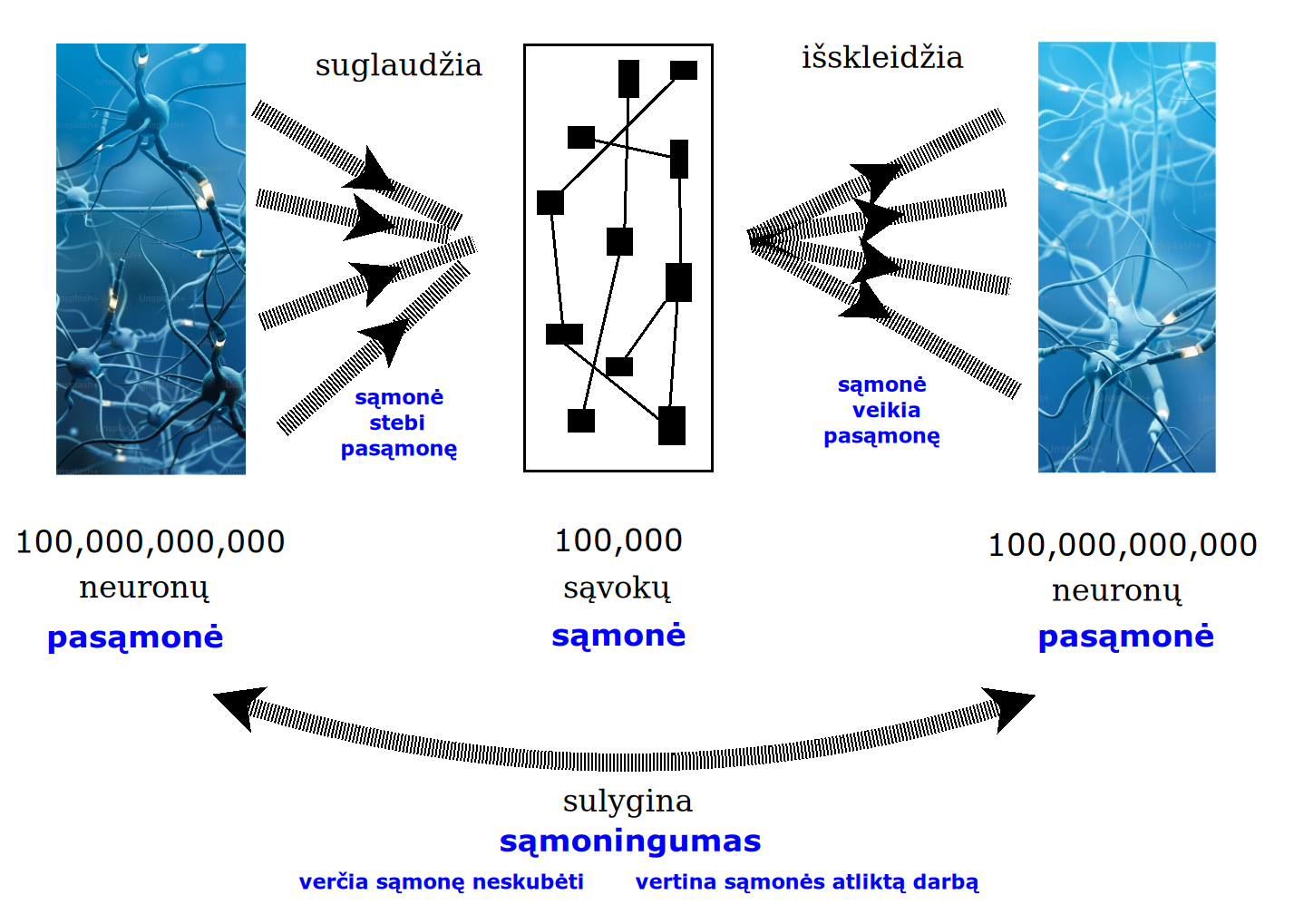
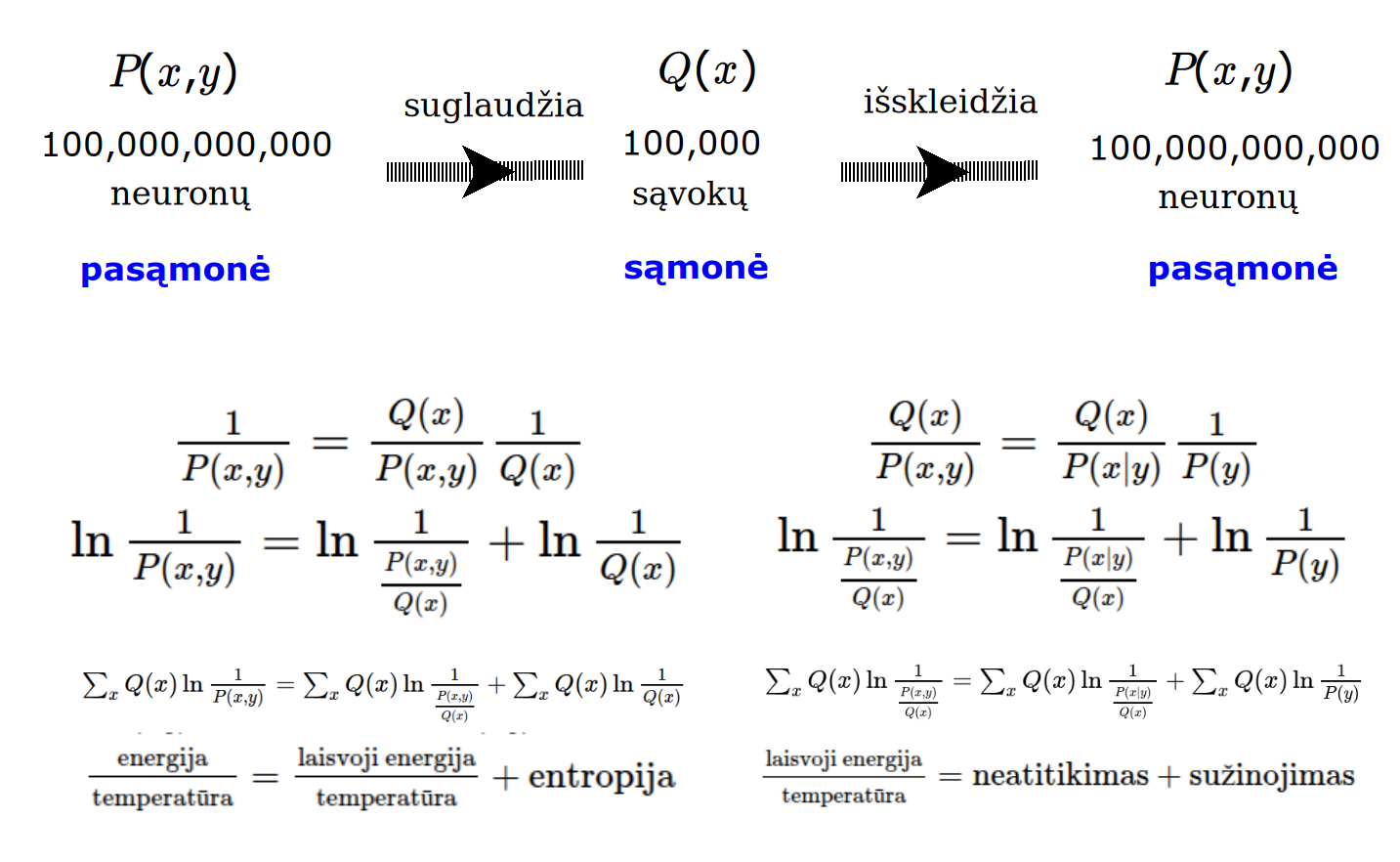
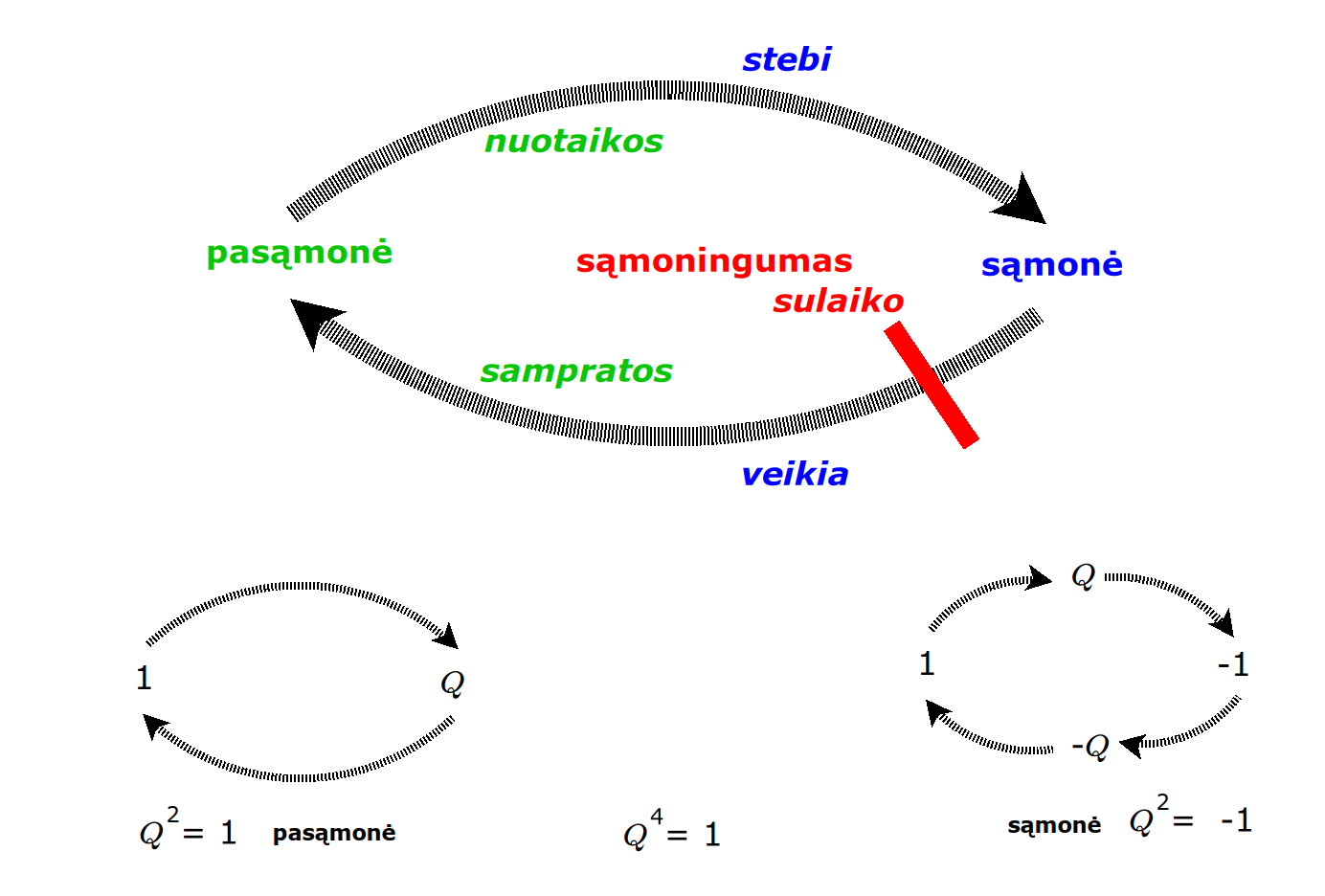
Žmogaus vidinis gyvenimas yra sunkiai nusakomas. Kaip jį modeliuoti? Jį pristatome kaip pokalbį tarp trijų sąmoningumo lygmenų, kitaip tariant, trijų protų: atsakančio, klausiančio ir tiriančio, kuriuos žymiu atitinkamai |一, |二, |三. Pasąmonė |一 mums ištisai siūlo vaizdus, patirtis, įspūdžius, nuotaikas, reiškinius, pavyzdžius, galybę atsakymų, ką mes nesąmoningai žinome. Sąmonė |二, atitrūkusi nuo juslių, savo ruožtu pina ryšius tarp sąvokų, žodžių, sampratų, kuriais mes nežinome, užtat sąmoningai klausiame. Visavertis sąmoningumas |三, kuriuo gyvename rūpestingai, apgalvotai, valingai, sulygina pasąmonės žinojimą ir sąmonės nežinojimą, kad galėtumėme viską permąstyti šiais dviem skirtingais pavidalais, užtat bet kokiu atveju rinktis, ar vadovautis nuojauta |一 ar išnagrinėjimu |二. Trijų protų pokalbis įžvelgiamas psichologijoje, neurologijoje, evoliucijoje, o taip pat matematikoje, fizikoje, kibernetikoje bei inžinerijoje: Kalmano filtre, variaciniame autoenkoderyje, laisvosios energijos principe, kvantinėse simetrijose.

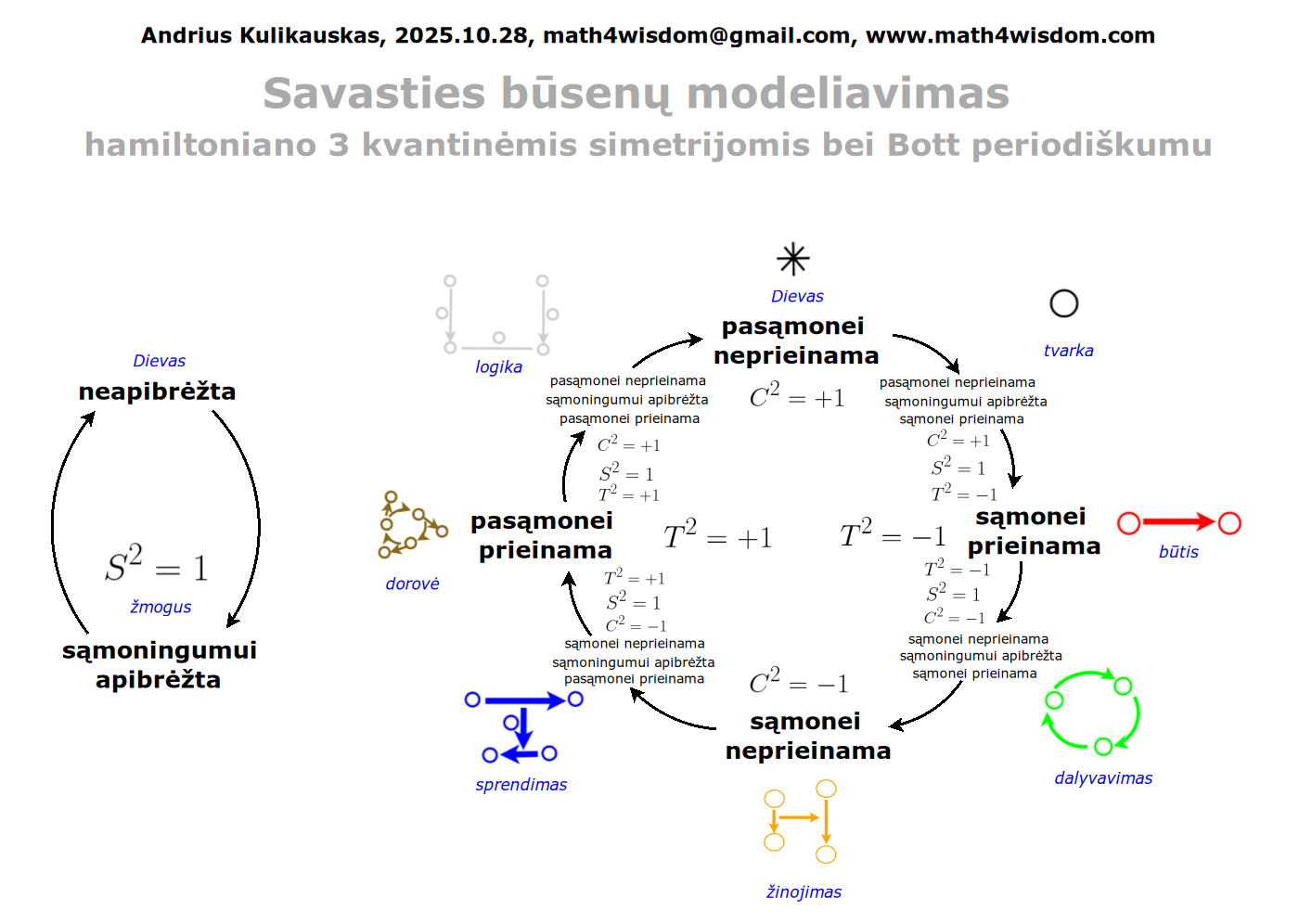
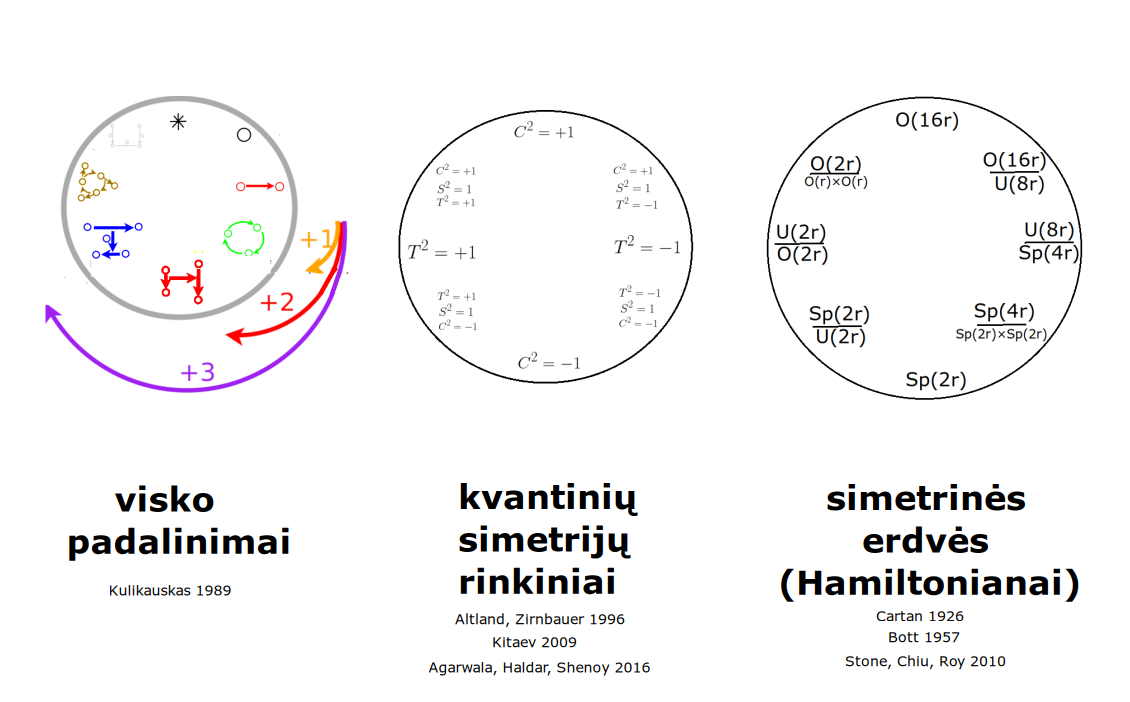
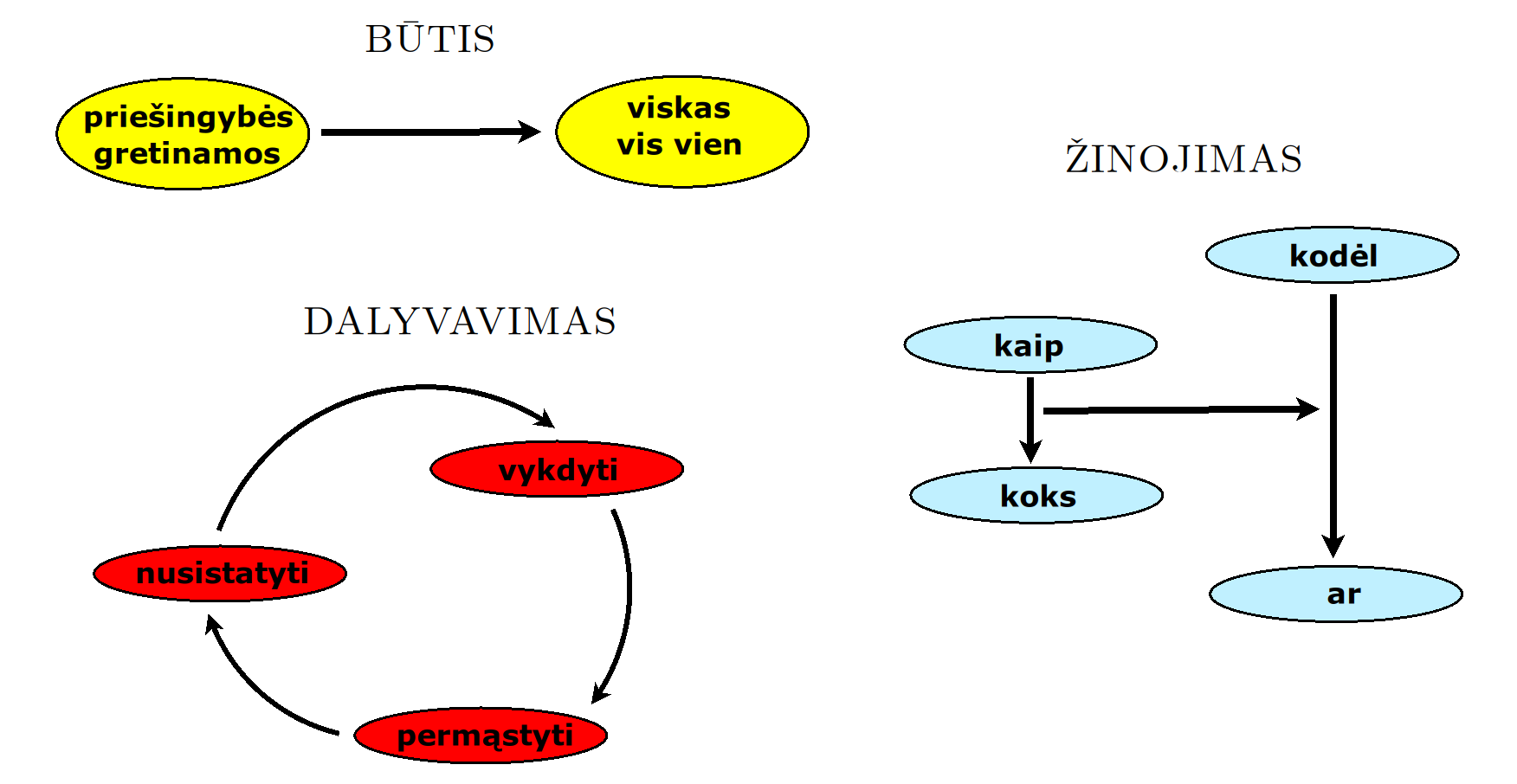
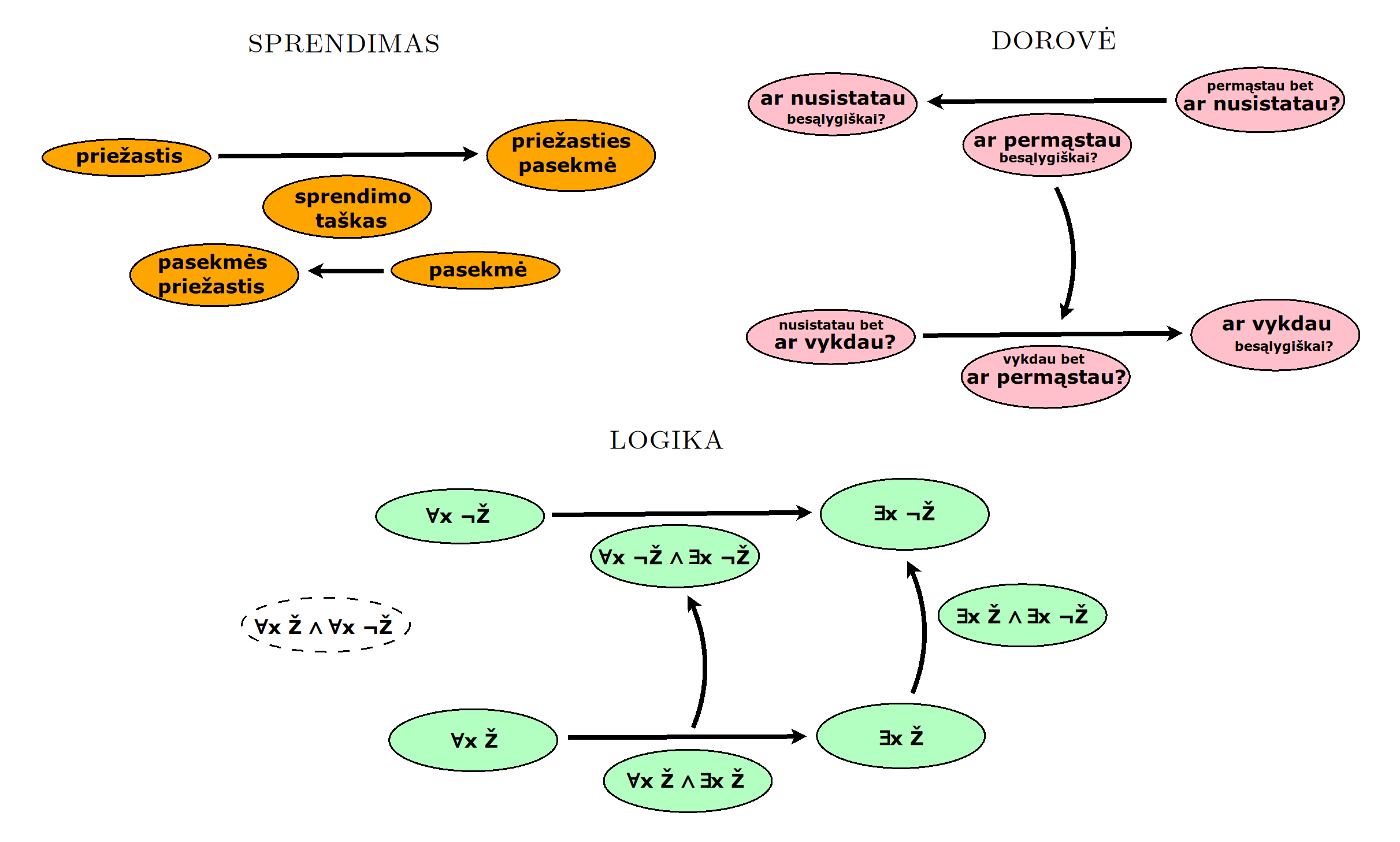
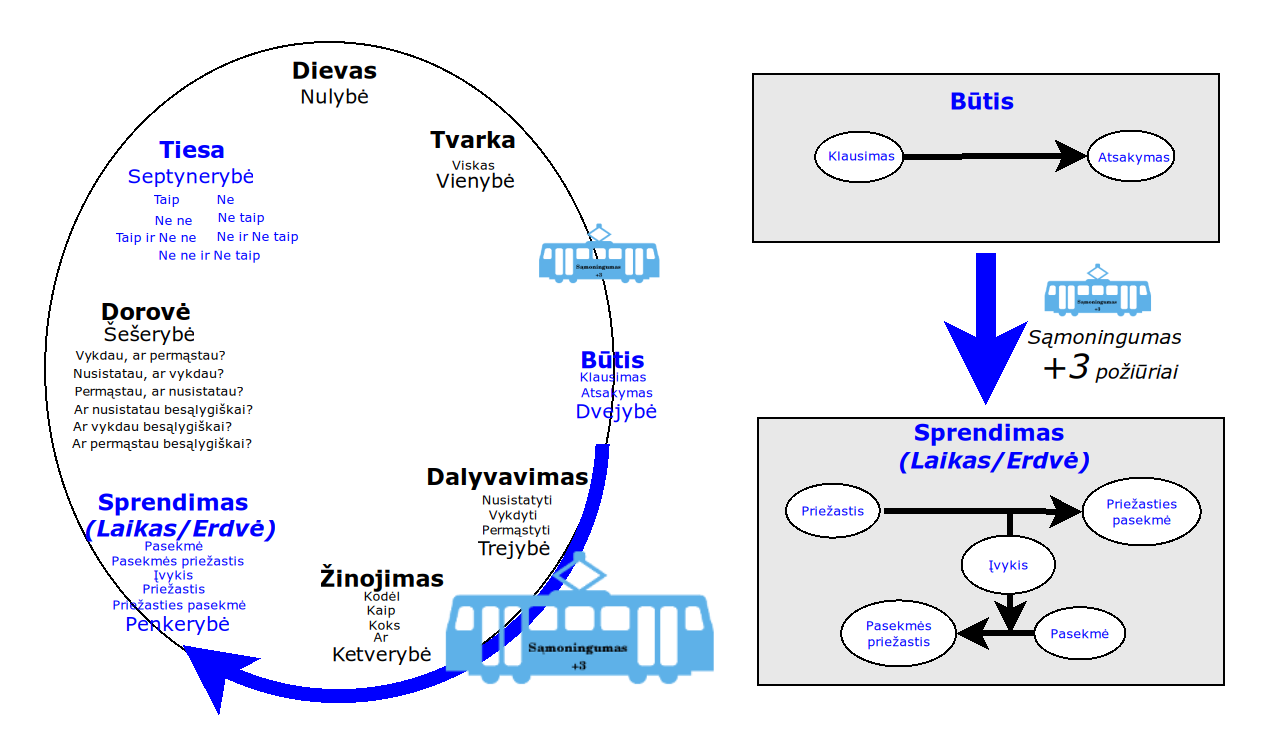
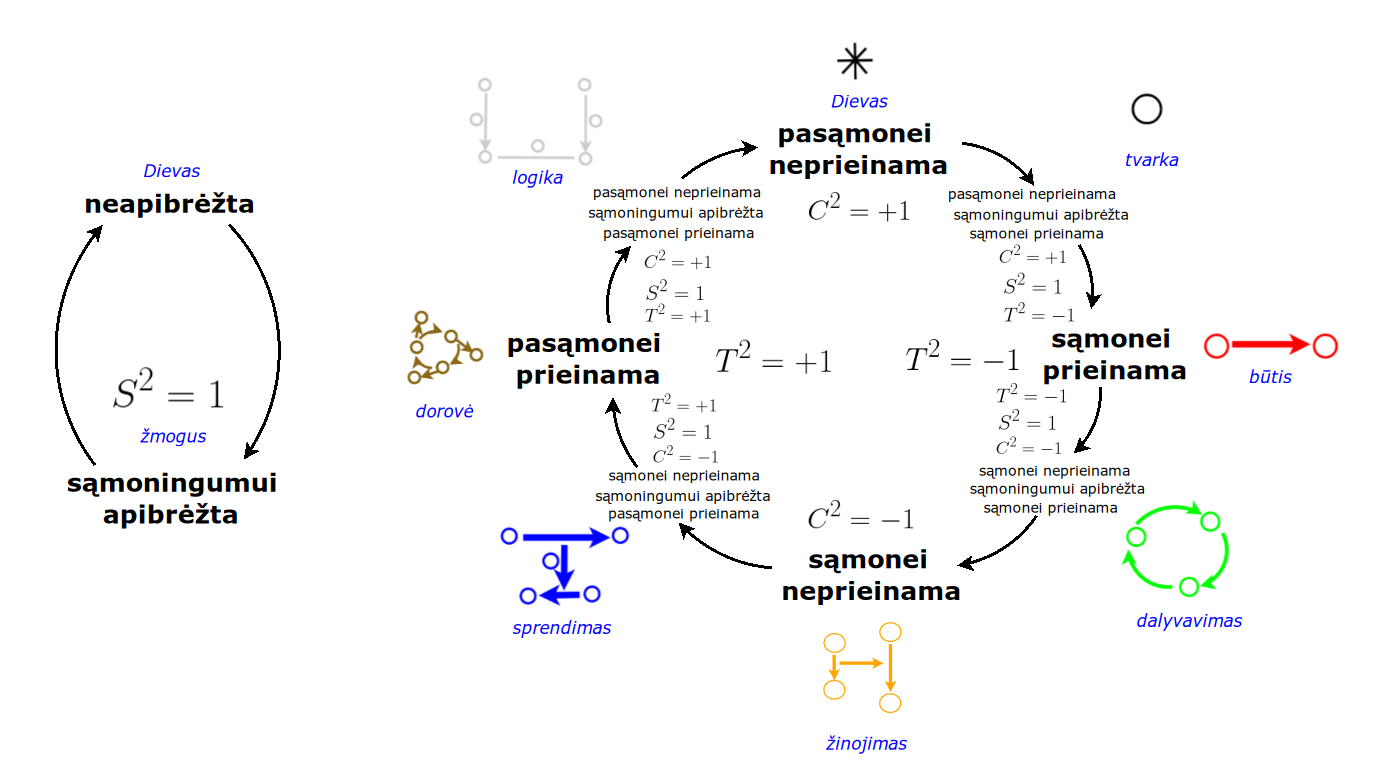
Atsisakydami visų pasąmonės |一 patirčių bei sąmonės |二 sampratų belieka susitelkti į miglų migloje betūnantį grynų gryniausią sąmoningumą |三, apčiuopiantį pirmaprades proto galimybes, pačias paprasčiausias proto sandaras, viską dalinančius į požiūrius. Atpažįstame būties klausimams reikalingą priešpastatymą (laisvos valios ir likimo), dalyvavimui reikalingą mokymosi ratą (nusistatome, vykdome, permąstome) ir žinojimui reikalingus lygmenis (ar, koks, kaip, kodėl). Galima apibrėžti ir kitus tokius visko padalinimus, o galiausiai pastebėti, kaip subliūkšta aštuntas visko padalinimas, logikos kvadratas, tvirtindamas "visi yra X ir visi nėra X", taip kad santvarka yra tuščia. Užtat visko padalinimai sudaro aštuonių proto aplinkų ratą. Ar toksai ratas pasireiškia matematikoje?

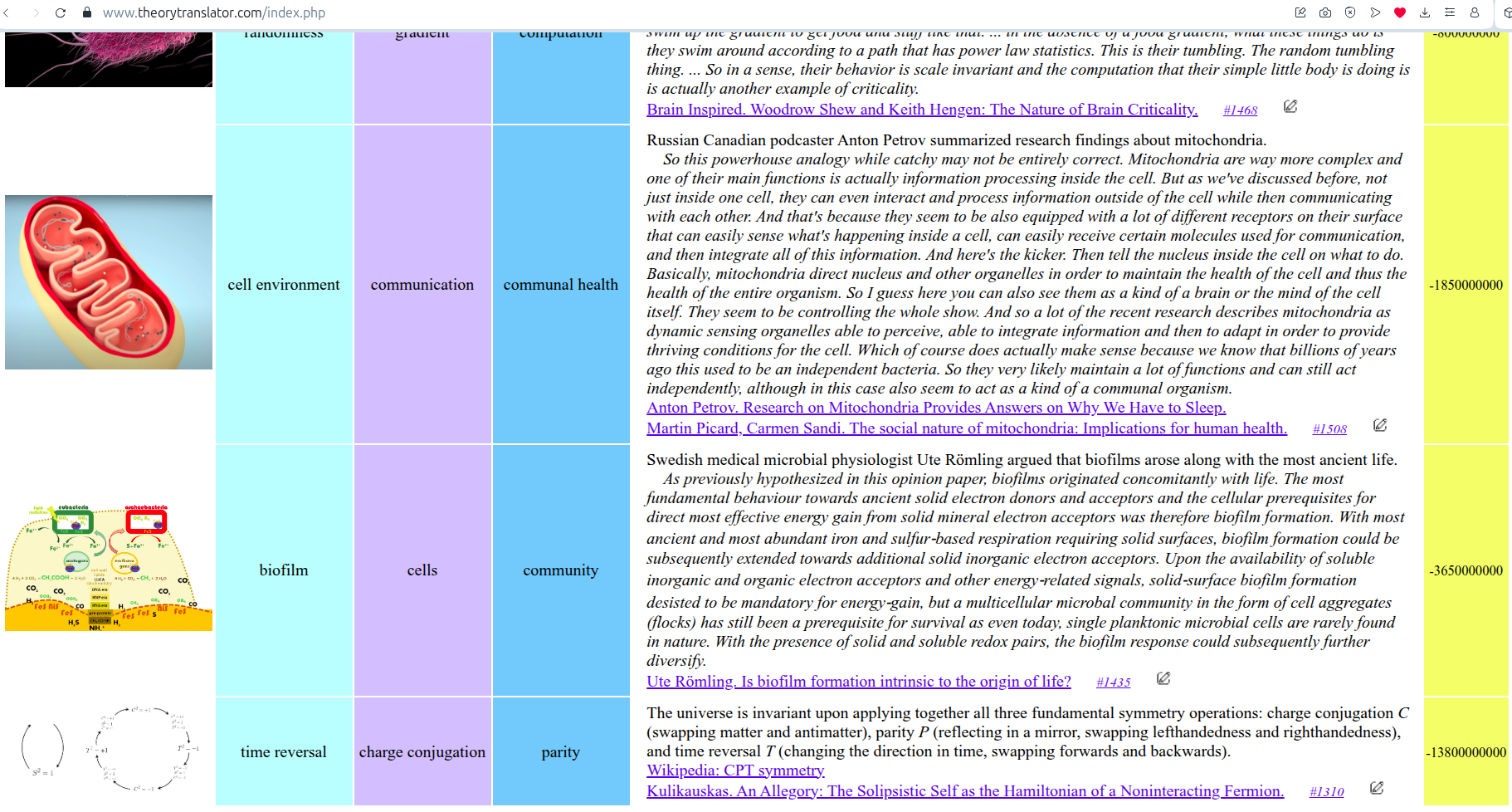
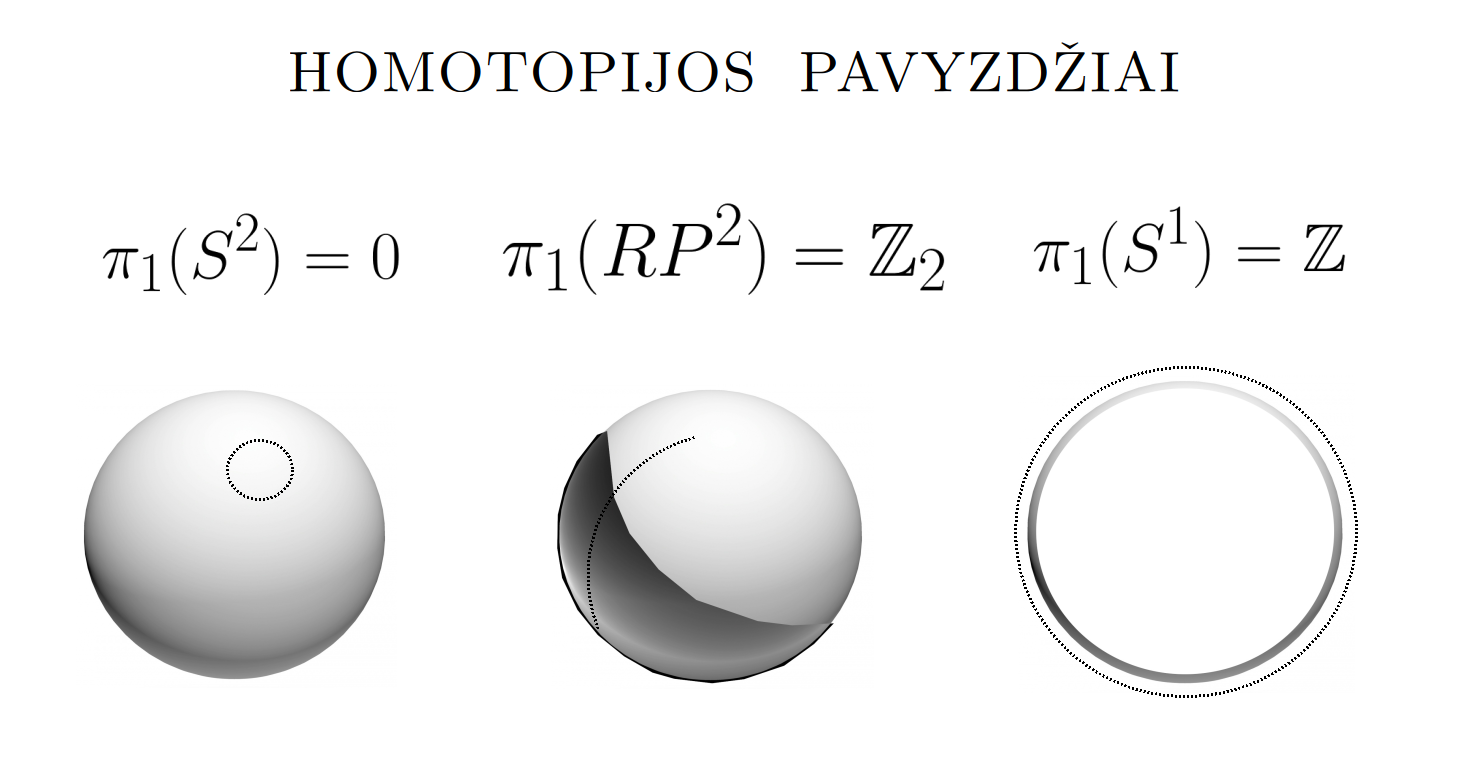
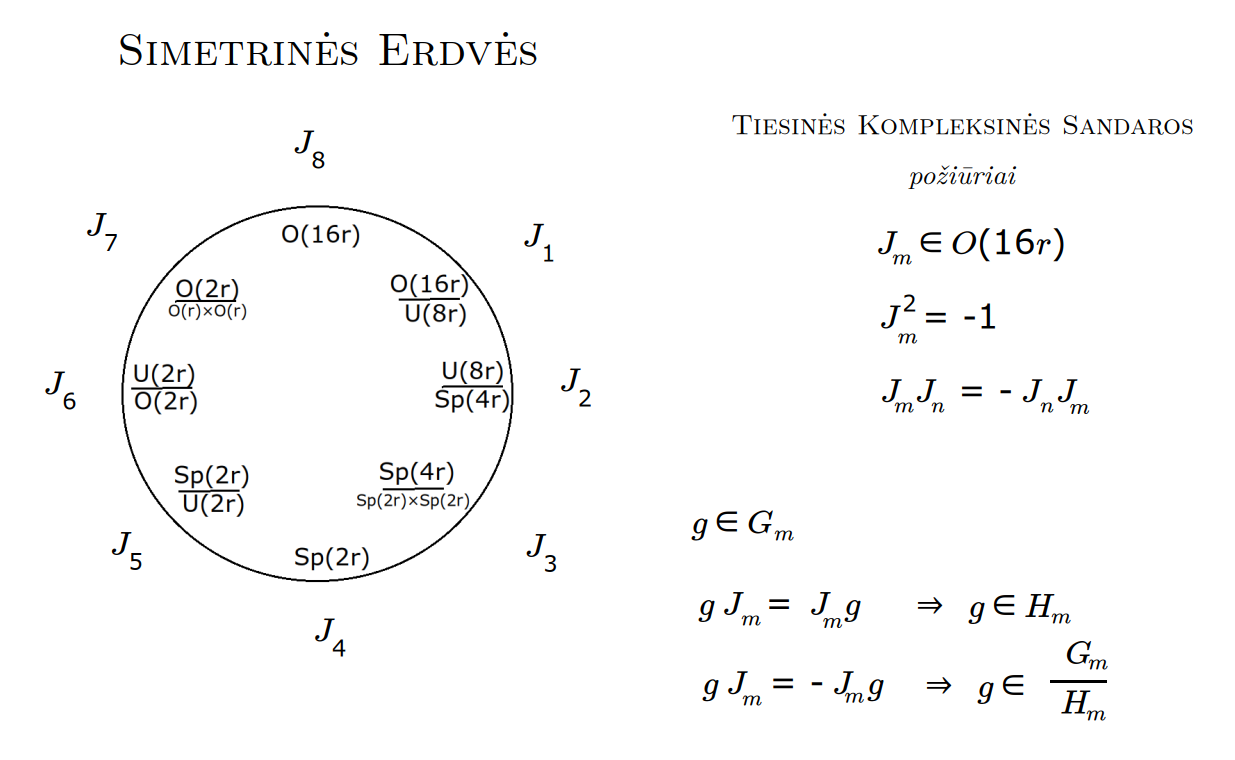
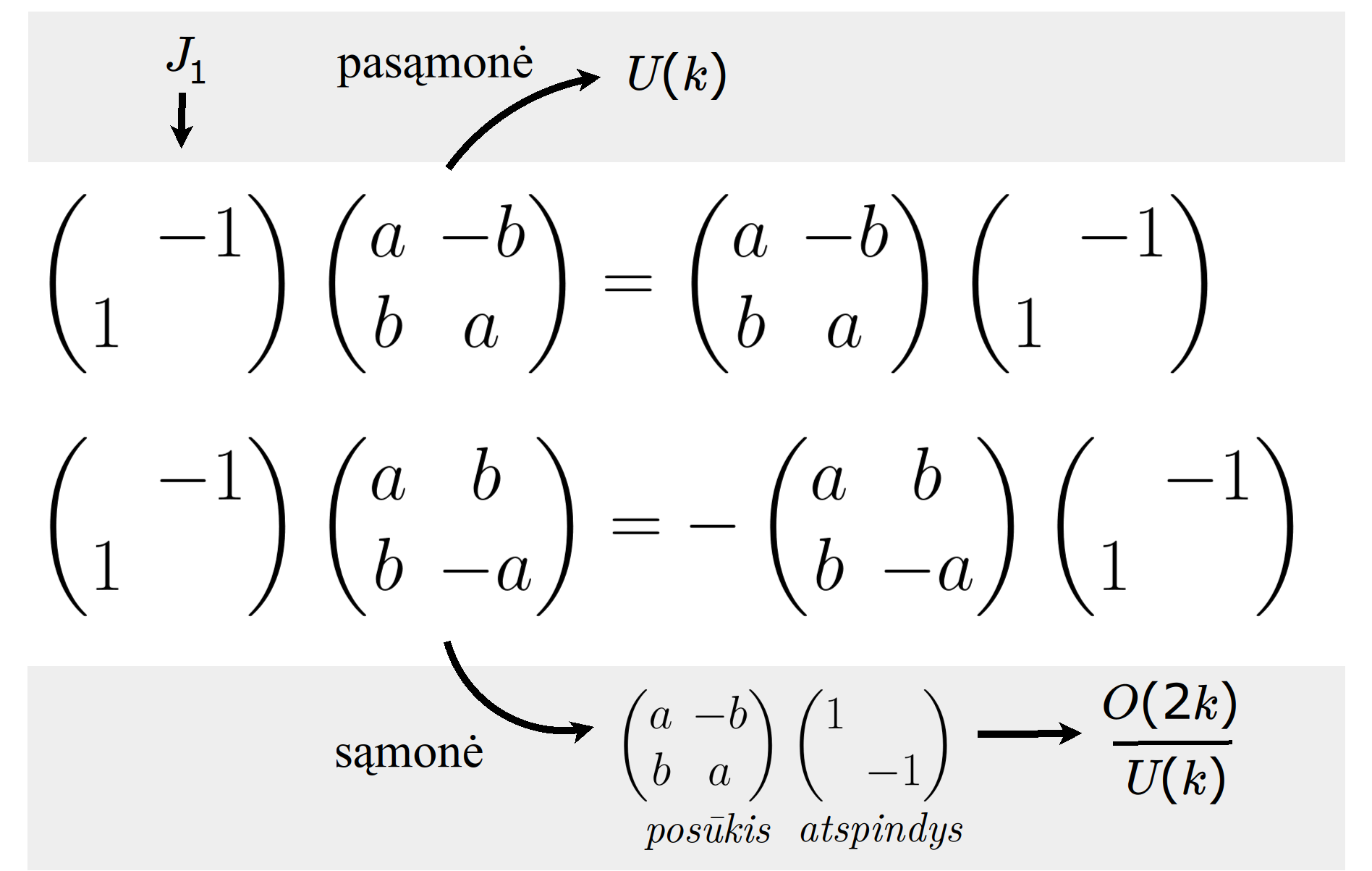
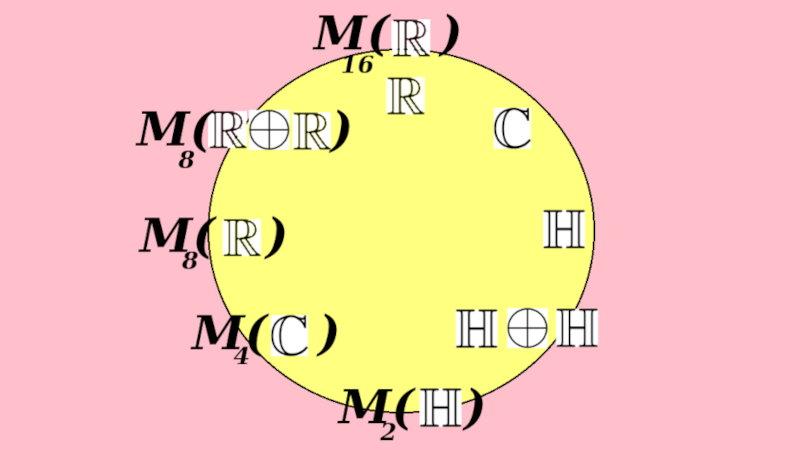
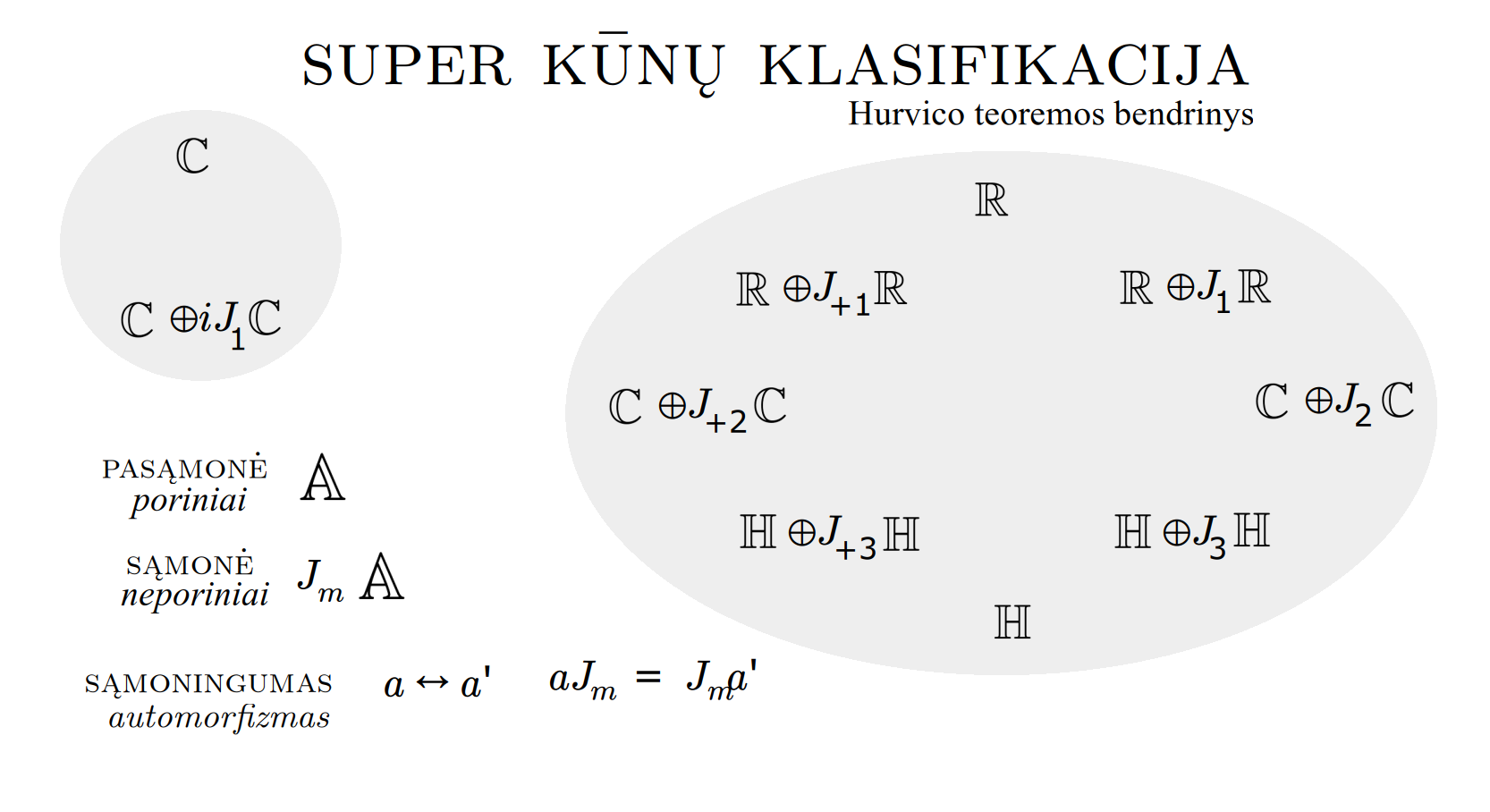
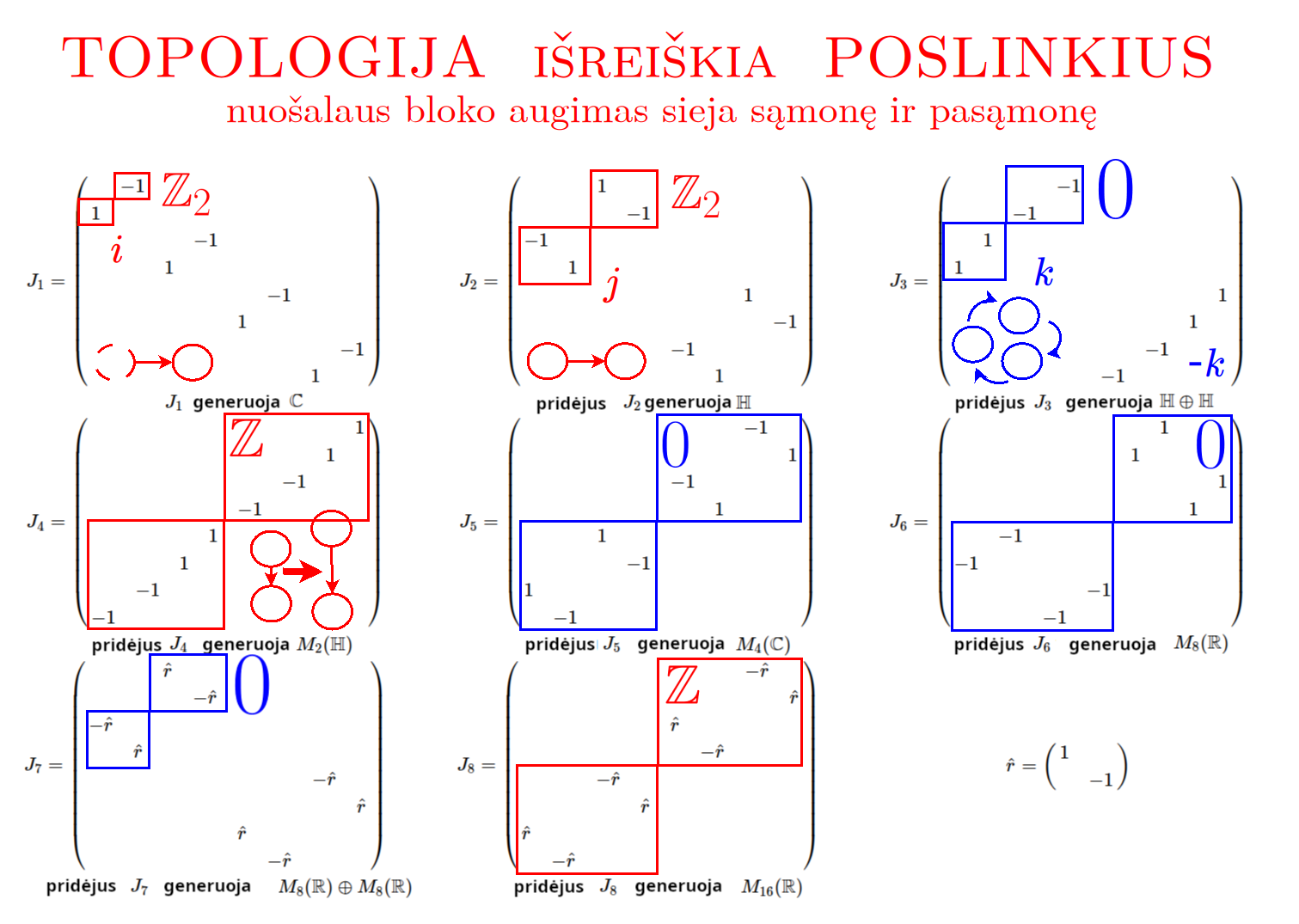
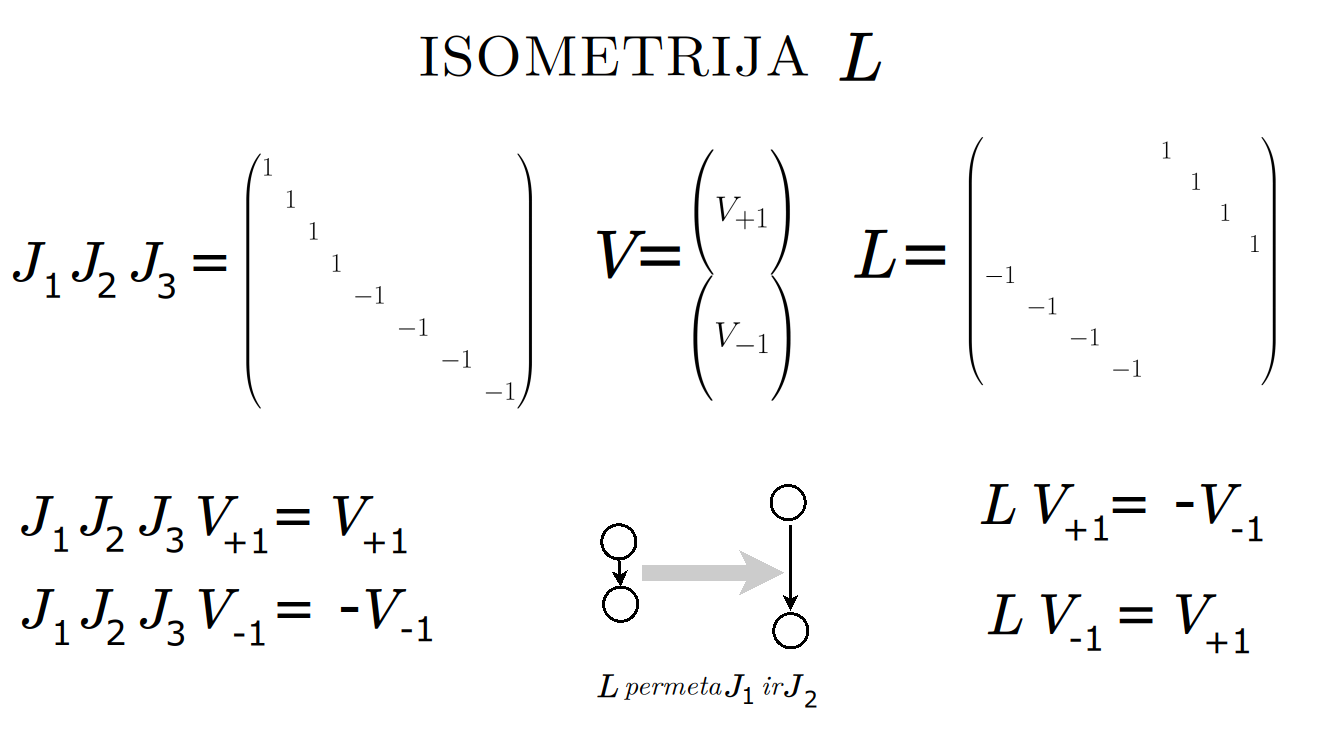
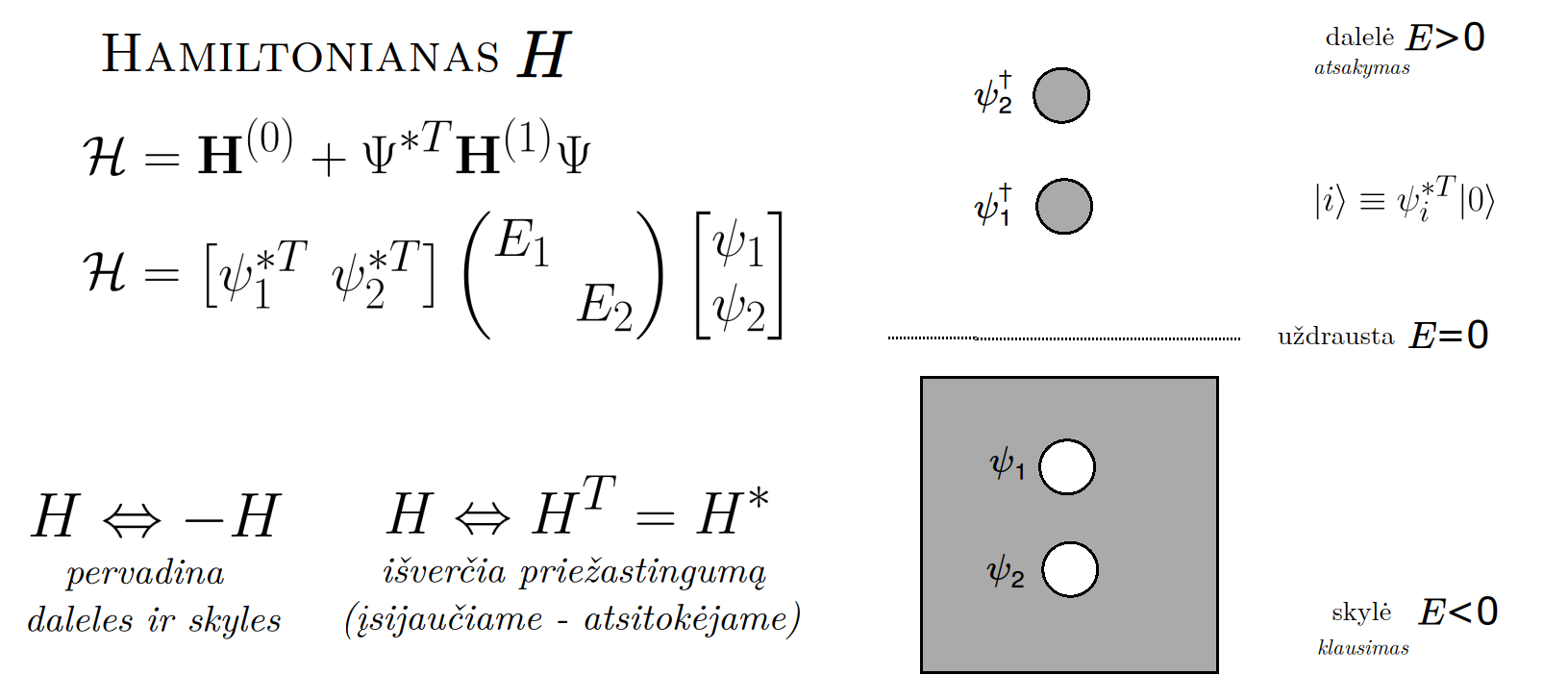
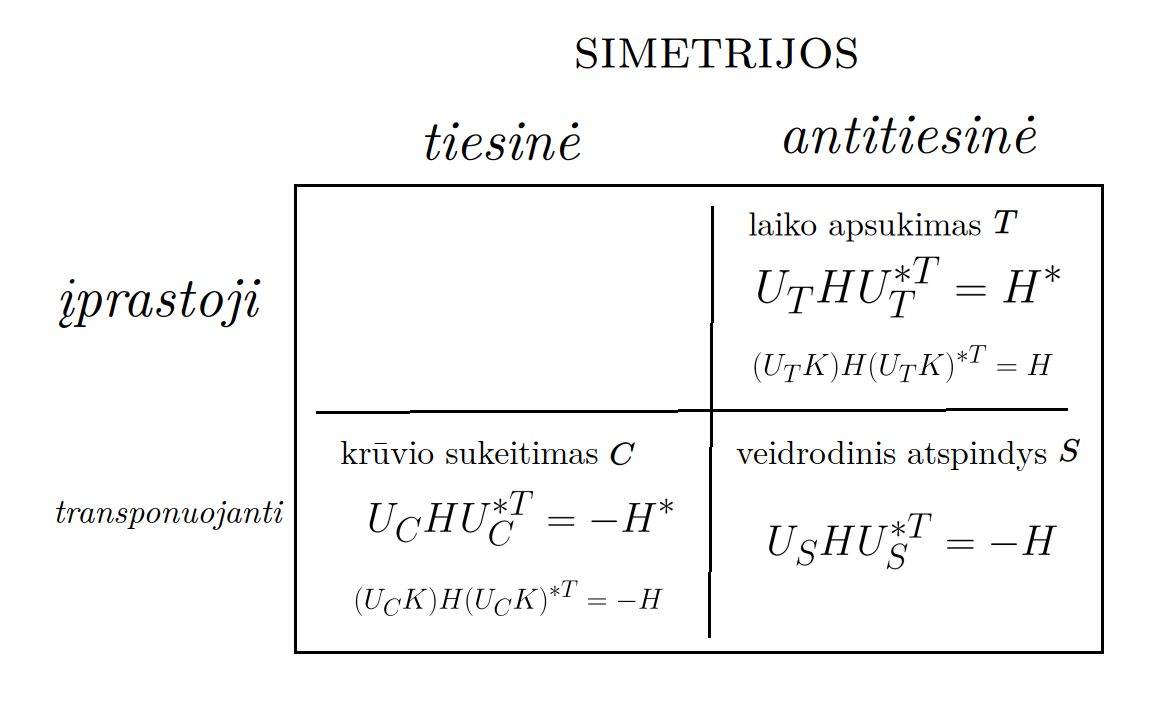
Matematikos širdyje, ar tiesiog jos bamboje, yra būtent panašus aštuonių būsenų ratas, realusis Bott periodiškumas, taip pat dviejų būsenų ratas, kompleksinis Bott periodiškumas. Juos galima suprasti dalykiškai kaip Lie algebrų įdėtis o(16r) ⊃ u(8r) ⊃ sp(4r) ⊃ sp(2r) × sp(2r) ⊃ sp(2r) ⊃ u(2r) ⊃ o(2r) ⊃ o(r) × o(r) ⊃ o(r) ir taipogi u(2r) ⊃ u(r) × u(r) ⊃ u(r). Šias įdėtis galima suprasti kaip visko padalinimus tiesinių kompleksinių struktūrų J_1, J_2, ... pagrindu, juos generuojant pagal Stone, Chiu, Roy (2011) receptą. O metafizinę prasmę galima išmąstyti suvokiant, kad abu Bott periodiškumai kartu išreiškia dešimtlypį kelią klasifikuojantį topologinius izoliatorius. Ši klasifikacija išsako kaip nesąveikaujančio fermiono hamiltonianas tenkina trijų kvantinių simetrijų (laiko apsukimo, krūvio sukeitimo, veidrodinio atspindžio) rinkinius, kurių iš viso yra dešimt. Hamiltoniano galimybes išnagrinėja Agarwala, Haldar, Shenoy (2017). Sulyginus šiuos skaičiavimus ir visko padalinimus galima suprasti nesąveikaujančio fermiono Hamiltonianą kaip modeliuojantį mūsų pačių savasčiai būdingas aplinkas, tai yra, būsenas.

Šias mintis išdėstau straipsnyje, "An Allegory: The Solipsistic Self as the Hamiltonian of a Noninteracting Fermion" https://www.math4wisdom.com/files/AnAllegory.pdf

Andrius Kulikauskas

Modeling the States of the Self with 3 Quantum Symmetries of a Hamiltionian and with Bott Periodicity

The inner life of a person is difficult to describe. How to model it? We present it as a conversation between three levels of consciousness, in other words, three minds: answering, asking, and investigating. The subconscious |一 continuously offers us images, experiences, impressions, moods, phenomena, examples, a multitude of answers, which we unconsciously know. The conscious |二, detached from the senses, in turn weaves connections between concepts, words, notions, which we do not know, but which we consciously ask. Full-fledged consciousness |三, which we live with care, thoughtfulness, will, compares the knowledge of the subconscious and the ignorance of consciousness, so that we can rethink everything in these two different forms, therefore, in any case, choose whether to be guided by intuition |一 or analysis |二. The conversation of the three minds is seen in psychology, neuroscience, evolution, as well as in mathematics, physics, cybernetics and engineering: the Kalman filter, the variational autoencoder, the free energy principle, quantum symmetries.

By abandoning all concepts of the subconscious |一 experiences and consciousness |二, we can only focus on the purest consciousness |三, which lies in the mist of mist, grasping the primordial possibilities of the mind, the simplest structures of the mind, dividing everything into points of view. We recognize the opposition necessary for questions of being (free will and fate), the circle of learning necessary for participation (we determine, we perform, we rethink), and the levels necessary for knowledge (whether, what, how, why). One can define other such divisions of everything, and finally observe how the eighth division of everything, the square of logic, collapses, asserting "all are X and all are not X", so that the system is empty. Instead, the divisions of everything form a circle of eight mental environments. Does such a circle manifest itself in mathematics?

At the heart of mathematics, or simply its navel, is precisely a similar circle of eight states, the real Bott periodicity, as well as a circle of two states, the complex Bott periodicity. They can be understood practically as the embeddings of the Lie algebras o(16r) ⊃ u(8r) ⊃ sp(4r) ⊃ sp(2r) × sp(2r) ⊃ sp(2r) ⊃ u(2r) ⊃ o(2r) ⊃ o(r) × o(r) ⊃ o(r) and also u(2r) ⊃ u(r) × u(r) ⊃ u(r). These embeddings can be understood as partitions of everything based on linear complex structures J_1, J_2, ..., generated according to the recipe of Stone, Chiu, Roy (2011). And the metaphysical meaning can be thought of by realizing that both Bott periodicities together express a ten-way classification of topological insulators. This classification expresses how the Hamiltonian of a non-interacting fermion satisfies sets of three quantum symmetries (time reversal, charge conjugation, parity), of which there are ten in total. The possibilities of the Hamiltonian are explored by Agarwala, Haldar, Shenoy (2017). By comparing these calculations and the partitions of everything, one can understand the Hamiltonian of a non-interacting fermion as modeling our own intrinsic environments, that is, states.

I present these ideas in the article, "An Allegory: The Solipsistic Self as the Hamiltonian of a Noninteracting Fermion" https://www.math4wisdom.com/files/AnAllegory.pdf

Įvadas