- Recently changed pages
- News Archive
- Math4Wisdom at Jitsi
- News at BlueSky
- News at Mathstodon
- Research Notes
Study Groups
Featured Investigations
Featured Projects
Contact
- Andrius Kulikauskas
- m a t h 4 w i s d o m @
- g m a i l . c o m
- +370 607 27 665
- Eičiūnų km, Alytaus raj, Lithuania
Thank you, Participants!
Thank you, Veterans!
- Jon and Yoshimi Brett
- Dave Gray
- Francis Atta Howard
- Jinan KB
- Christer Nylander
- Kirby Urner
Thank you, Commoners!
- Free software
- Open access content
- Expert social networks
- Patreon supporters
- Jere Northrop
- Daniel Friedman
- John Harland
- Bill Pahl
- Anonymous supporters!
- Support through Patreon!
Bott Periodicity Models Consciousness? Preliminary Exploration
Overviewing Bott periodicity
I am exploring whether and how Bott periodicity may express the eight-cycle of mental states, the divisions of everyting.
The Origins in Homotopy Theory
In algebraic topology, given an {$n$}-sphere {$S^n$} with base point {$a$}, and a space {$X$} with base point {$b$}, the homotopy group {$\pi_n(X)$} is the set of homotopy classes of maps {$f:S^n\rightarrow X$} for which {$f(a)=b$}.
In 1959, Bott showed, using Morse theory, that if {$O(\infty)$} is defined as the inductive limit of the orthogonal groups, then its homotopy groups are periodic:
{$\pi_{n}(O(\infty))\simeq\pi_{n+8}(O(\infty))$}
The first 8 homotopy groups are as follows:
{$\begin{align} \pi_{0}(O(\infty))&\simeq Z_2 \\ \pi_{1}(O(\infty))&\simeq Z_2 \\ \pi_{2}(O(\infty))&\simeq 0 \\ \pi_{3}(O(\infty))&\simeq Z \\ \pi_{4}(O(\infty))&\simeq 0 \\ \pi_{5}(O(\infty))&\simeq 0 \\ \pi_{6}(O(\infty))&\simeq 0 \\ \pi_{7}(O(\infty))&\simeq Z \end{align}$}
The homotopy groups of spheres, {$\pi_i(S^n)$}, describe how spheres of various dimensions can wrap around each other.
When {$k\geq 2$}, an important subgroup of {$\pi_{n+k}(S_n)$} is the image of the J-homomorphism {$J:\pi_k(SO(n)) \rightarrow \pi_{n+k}(S_n)$}. In the stable range {$n\geq k+2$}, the homotopy groups {$\pi_k(SO(n))$} only depend on {$k \;\textrm{mod} \; 8$}.
The period 8 pattern is reflected via the image of the {$J$}-homomorphism, which is:
- a cyclic group of order {$2$} if {$k$} is congruent to {$0, 1 \; \textrm{mod}\; 8$};
- trivial if {$k$} is congruent to {$2, 4, 5, 6 \; \textrm{mod}\; 8$};
- a cyclic group of order equal to the denominator of {$\frac{B_{2m}}{4m}$} if {$k$} is congruent to {$3, 7 \; \textrm{mod}\; 8$}.
{$B_{2m}$} is a Bernoulli number. It is used to count sums of powers and is related to the Riemann-Zeta function.
{$B_{2m}=(-1)^{m-1}\frac{2m}{4^{2m}-2^{2m}}A^{2m-1}$}
where {$A^{2m-1}$} counts the number of alternating permutations of the set {$\{1,\cdots ,2m-1\}$}. These are permutations where each entry is alternately greater or less than the previous entry. There are {$5$} alternating permutations of {$\{1,2,3,4\}$}:
- {$1 < 3 > 2 < 4$}
- {$1 < 4 > 2 < 3$}
- {$2 < 3 > 1 < 4$}
- {$2 < 4 > 1 < 3$}
- {$3 < 4 > 1 < 2$}
Divisions of Everything
Here are two academic presentations that I have given about this eight-cycle of divisions of everything.
- Time and Space as Representations of Decision Making
- Consciousness as the Social Awareness Schema of a Disembodying Mind
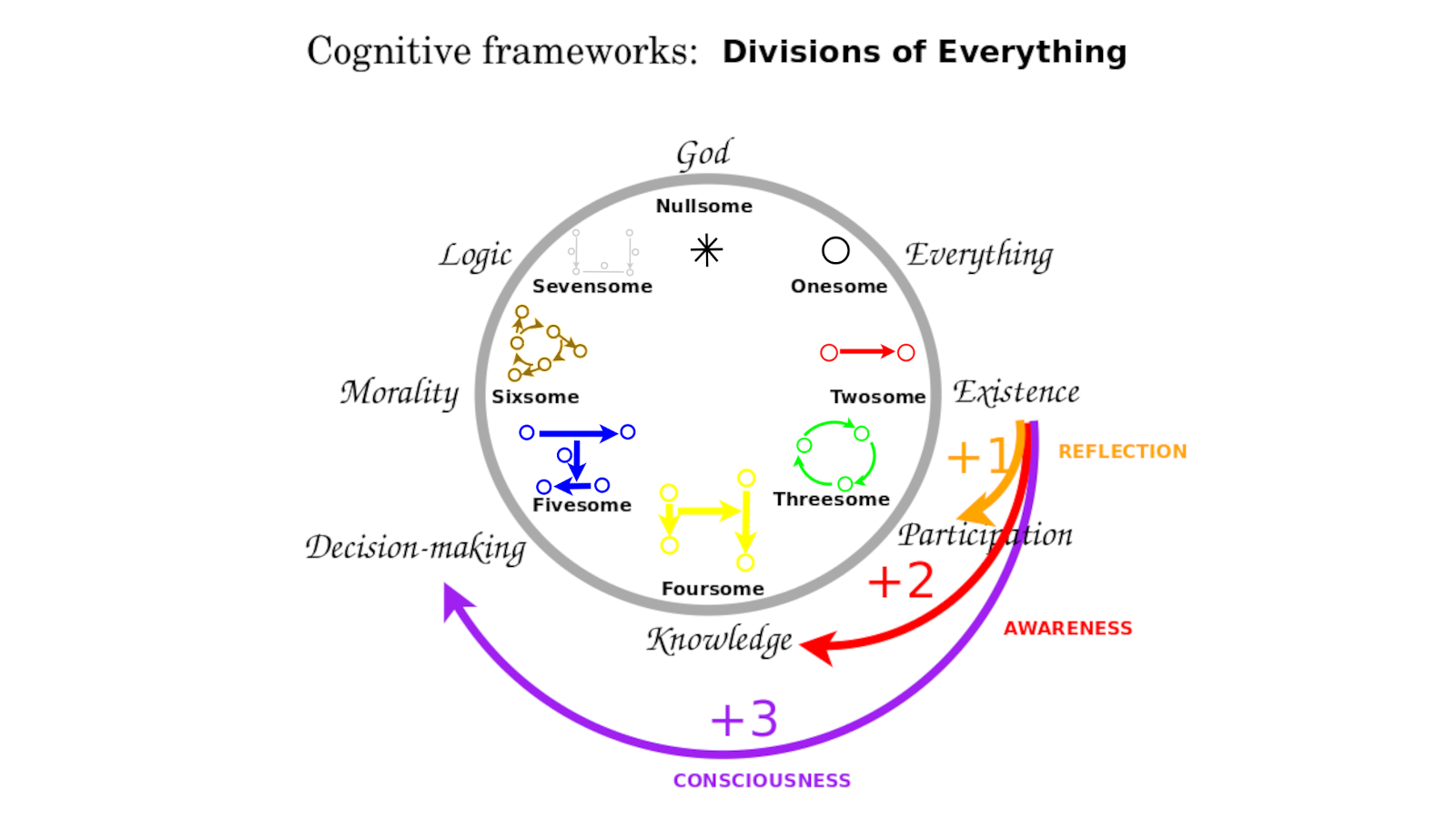
Bott periodicity has many manifestations
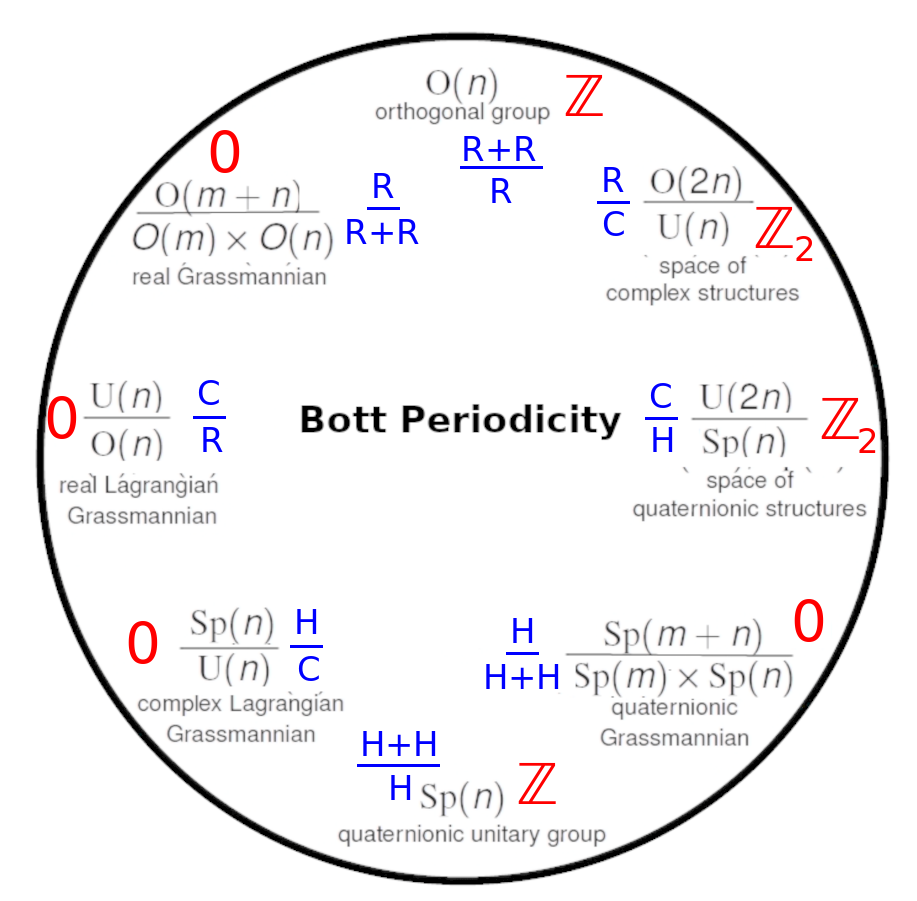
Bott periodicity, considered broadly, refers to an eightfold periodicity of
- Morita equivalence classes of real Clifford algebras
- Classical families of compact symmetric spaces
- Topological insulators - ways that Hamiltonians can get along with time reversal (T) and charge conjugation (C) symmetry. Defined by three symmetries of the Hamiltonian {$\hat{H}=\sum _{i,j}H_{ij}c_{i}^{\dagger }c_{j}$}, (where {$c_{i}$}, and {$ c_{i}^{\dagger }$}, are the annihilation and creation operators of mode {$i$}, in some arbitrary spatial basis) : time reversal symmetry, particle hole (or charge conjugation) symmetry, and chiral (or sublattice) symmetry.
- Ten Altland–Zirnbauer classes of random matrices. Described in Bernard, LeClair. A Classification of Non-Hermitian Random Matrices
- Ways that antiunitary operators (and, in the complex case, the unitary operators) commute with an irreducible unitary representation of a supergroup on a super Hilbert space
- Associative real super division algebras
- Complex spin representations
- Real spin representations
- Homotopy groups of {$O(\infty)$}
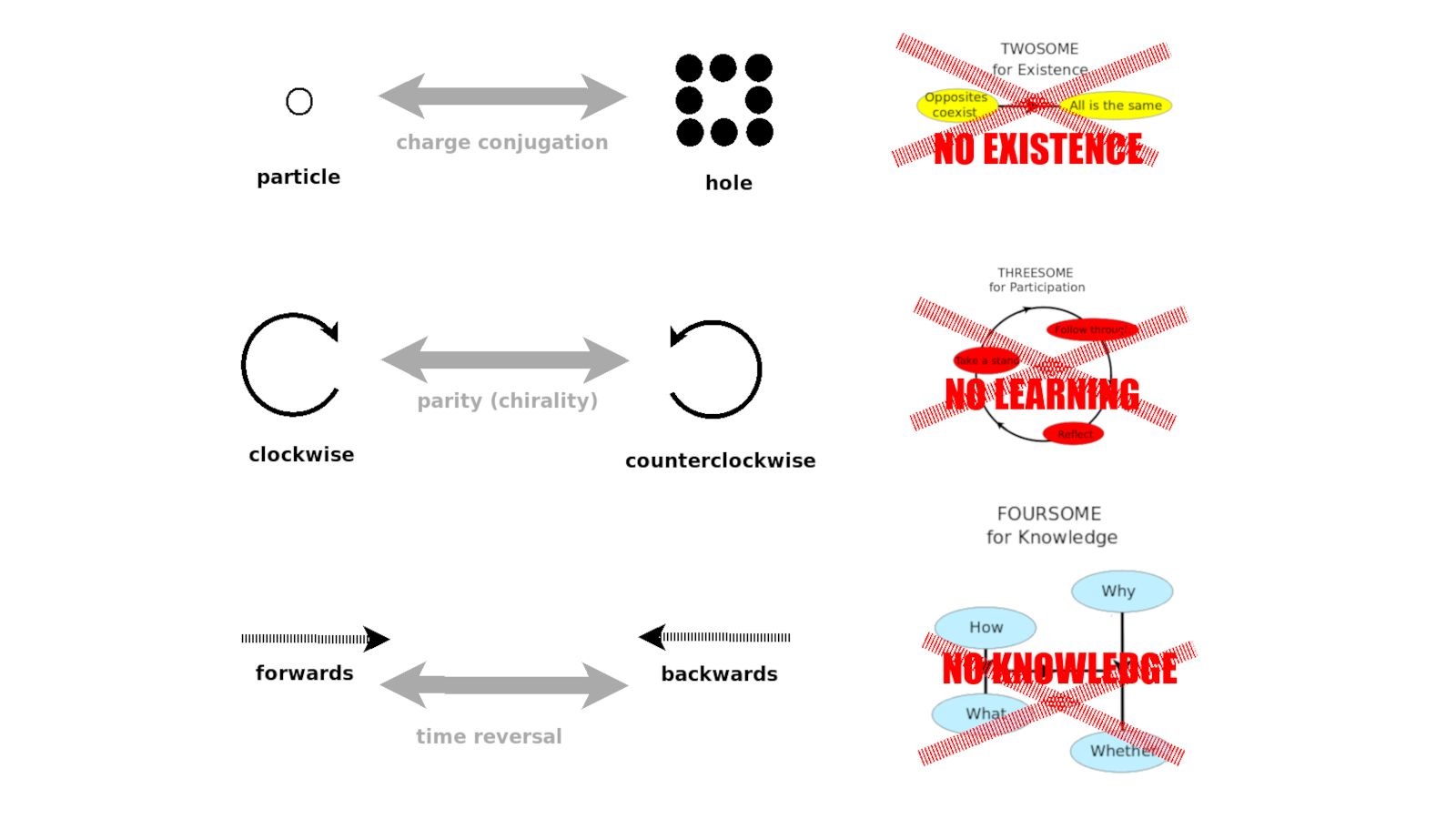

These refer to entities over the real numbers. There also is a twofold Bott periodicity for entities over the complex numbers. Together they constitute what is known as the tenfold way, for example, of topological insulators.
Taken together these ten things form the Brauer-Wall monoid of {$\mathbb{R}$}.
{$O \times O \subset O \subset U\subset \operatorname{Sp} \subset \operatorname{Sp} \times \operatorname{Sp} \subset \operatorname{Sp} \subset U \subset O \subset O \times O$}
{$U \times U \subset U \subset U \times U$}
Clifford algebras over real numbers or quaternions:
{$\mathbb{R} \oplus \mathbb{R} \subset \mathbb{R} \subset \mathbb{C} \subset \mathbb{H} \subset \mathbb{H} \oplus \mathbb{H} \subset \mathbb{H} \subset \mathbb{C} \subset \mathbb{R} \subset \mathbb{R} \oplus \mathbb{R}$}
Clifford algebras over complex numbers:
{$\mathbb{C} \oplus \mathbb{C} \subset \mathbb{C} \subset \mathbb{C} \oplus \mathbb{C} $}
Bott periodicity is at the center of mathematics
Lie theory unites algebra and analysis by way of geometry
Classical Lie families
Expressing the symmetries inherent in math itself
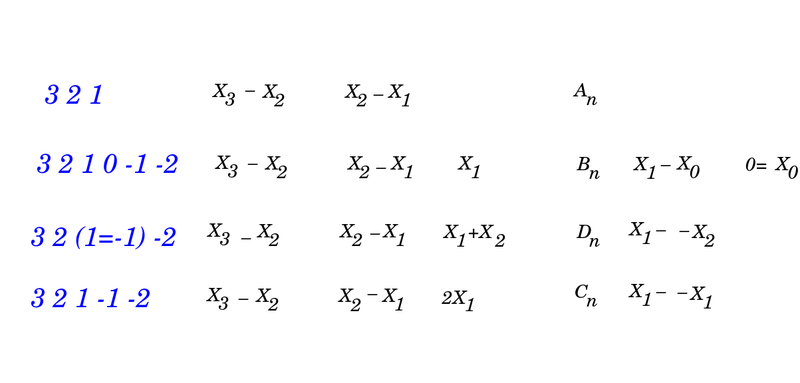
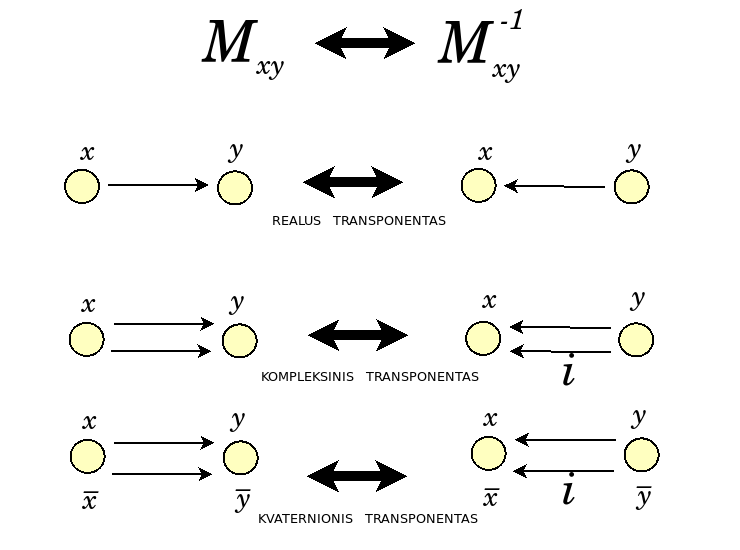
The Ways Modules Fit Together
- M.F.Atiyah, R.Bott, A.Shapiro | Clifford Modules.
- Dexter Chua. Clifford Algebras and Bott Periodicity.
- Dale Husemoller. Fiber Bundles.
- Andrius: Clifford Algebras.
Speak of representations, or in the case of quaternions, modules.
By Wedderburn, a matrix algebra of {$R$}, {$C$} or {$H$} has only one irreducible representation, the natural representation.
{$\mathbb{Z}_2$} is how the reals fit within the complexes, and how the complexes fit within the quaternions$}
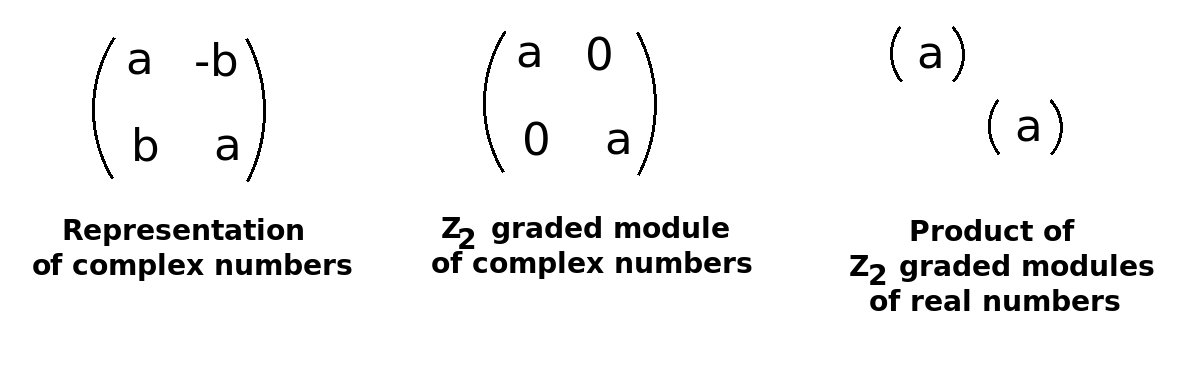
By Wedderburn, there are two representations of {$R\oplus R$}, of {$C\oplus C$} and of {$H\oplus H$}
{$\mathbb{Z}$} is how the two representations of {$R\oplus R$} fit within the one representation of {$M_2(R)$}
0, the trivial group, says that the representations of one Clifford algebra and the next Clifford algebra have the same size
Clifford algebras
Clifford algebras extend the binomial theorem
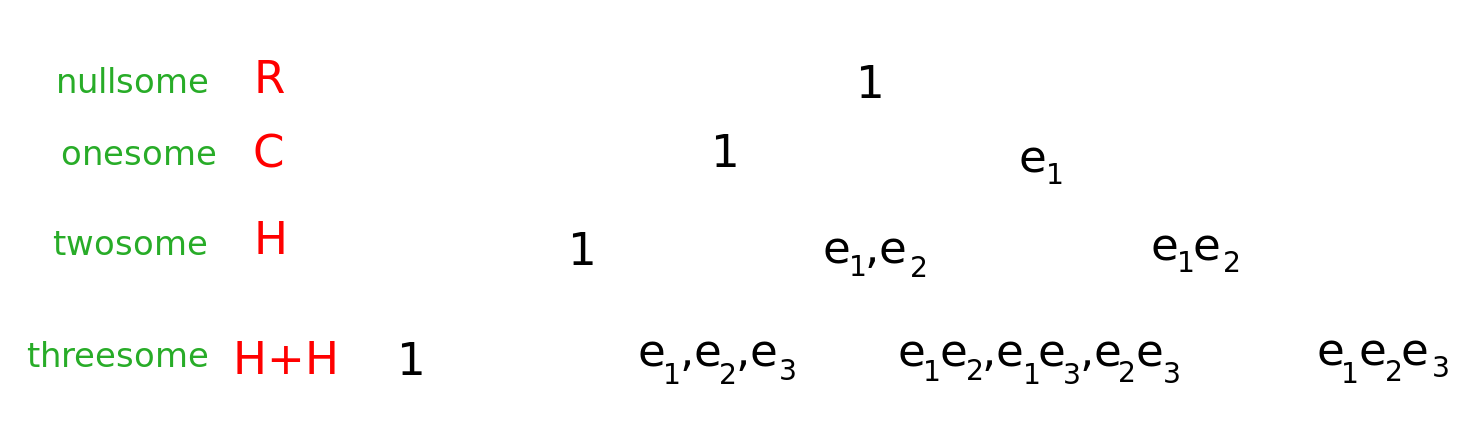
A Clifford algebra is a row in Pascal's triangle. Thus the dimension for the {$k$}th row is {$2^k$}.
We interpret this as the choices to include {$e_i$} or not. This means that the two extremes - the empty center {$1$} and the totality (pseudoscalar) {$e_1e_2\cdots e_k$} are asymmetric, as with simplexes, as in the video Binomial Theorem Is a Portal to Your Mind.
Add relations
- {$e_i^2=-1$} or {$+1$} or {$0$}.
- {$e_ie_j = - e_je_i$} for {$i\neq j$}.
The latter equation can be used to try to make sense of the value of {$e_1^2$}.
Patterns
- The square of the pseudoscalar.
- Whether the pseudoscalar commutes.
Understanding Clifford algebras in terms of matrices of numbers (real, complex, quaternions)
- {$\textrm{Cl}_{p+2,q}(\mathbf{R}) = \mathrm{M}_2(\mathbf{R})\otimes \textrm{Cl}_{q,p}(\mathbf{R}) $}
- {$\textrm{Cl}_{p+1,q+1}(\mathbf{R}) = \mathrm{M}_2(\mathbf{R})\otimes \textrm{Cl}_{p,q}(\mathbf{R}) $}
- {$\textrm{Cl}_{p,q+2}(\mathbf{R}) = \mathbf{H}\otimes \textrm{Cl}_{q,p}(\mathbf{R}) $}
This yields the following sequences:
| {$\textrm{Cl}_{0,0}(\mathbf{R})$} | {$=\mathbb{R}$} | {$=\mathbb{R}$} | {$\textrm{Cl}_{0,0}(\mathbf{R})$} | {$=\mathbb{R}$} | {$=\mathbb{R}$} |
| {$\textrm{Cl}_{0,2}(\mathbf{R})$} | {$\cong\mathbb{H}\otimes\mathbb{R}$} | {$\cong\mathbb{H}$} | {$\textrm{Cl}_{2,0}(\mathbf{R})$} | {$\cong M_2(\mathbb{R})\otimes \mathbb{R}$} | {$\cong M_2(\mathbb{R})$} |
| {$\textrm{Cl}_{0,4}(\mathbf{R})$} | {$\cong \mathbb{H}\otimes M_2(\mathbb{R})\otimes \mathbb{R}$} | {$\cong M_2(\mathbb{H})$} | {$\textrm{Cl}_{4,0}(\mathbf{R})$} | {$\cong M_2(\mathbb{R})\otimes \mathbb{H} \otimes \mathbb{R}$} | {$\cong M_2(\mathbb{H})$} |
| {$\textrm{Cl}_{0,6}(\mathbf{R})$} | {$\cong\mathbb{H}\otimes M_2(\mathbb{R})\otimes\mathbb{H}\otimes\mathbb{R}$} | {$\cong M_4(\mathbb{H})$} | {$\textrm{Cl}_{6,0}(\mathbf{R})$} | {$\cong M_2(\mathbb{R})\otimes \mathbb{H} \otimes M_2(\mathbb{R})\otimes \mathbb{R}$} | {$\cong M_8(\mathbb{R})$} |
| {$\textrm{Cl}_{0,8}(\mathbf{R})$} | {$\cong \mathbb{H}\otimes M_2(\mathbb{R})\otimes\mathbb{H}\otimes M_2(\mathbb{R})\otimes\mathbb{R}$} | {$\cong M_{16}(\mathbb{R})$} | {$\textrm{Cl}_{8,0}(\mathbf{R})$} | {$\cong M_2(\mathbb{R})\otimes \mathbb{H} \otimes M_2(\mathbb{R})\otimes \mathbb{H} \otimes \mathbb{R}$} | {$\cong M_{16}(\mathbb{R})$} |
| {$\textrm{Cl}_{0,1}(\mathbf{R})$} | {$\cong\mathbb{C}$} | {$\cong\mathbb{C}$} | {$\textrm{Cl}_{1,0}(\mathbf{R})$} | {$\cong\mathbb{R}\oplus\mathbb{R}$} | {$\cong\mathbb{R}\oplus\mathbb{R}$} |
| {$\textrm{Cl}_{0,3}(\mathbf{R})$} | {$\cong\mathbb{H}\otimes(\mathbb{R}\oplus\mathbb{R})$} | {$\cong\mathbb{H}\oplus\mathbb{H}$} | {$\textrm{Cl}_{3,0}(\mathbf{R})$} | {$\cong M_2(\mathbb{R}) \otimes \mathbb{C}$} | {$\cong M_2(\mathbb{C})$} |
| {$\textrm{Cl}_{0,5}(\mathbf{R})$} | {$\cong \mathbb{H}\otimes M_2(\mathbb{R})\otimes \mathbb{C}$} | {$\cong M_4(\mathbb{C})$} | {$\textrm{Cl}_{5,0}(\mathbf{R})$} | {$\cong M_2(\mathbb{R})\otimes \mathbb{H}\otimes (\mathbb{R}\oplus\mathbb{R})$} | {$\cong M_2(\mathbb{H})\oplus M_2(\mathbb{H})$} |
| {$\textrm{Cl}_{0,7}(\mathbf{R})$} | {$\cong \mathbb{H}\otimes M_2(\mathbb{R})\otimes\mathbb{H}\otimes (\mathbb{R}\oplus\mathbb{R})$} | {$\cong M_8(\mathbb{R})\oplus M_8(\mathbb{R})$} | {$\textrm{Cl}_{7,0}(\mathbf{R})$} | {$\cong M_2(\mathbb{R})\otimes\mathbb{H}\otimes M_2(\mathbb{R})\otimes \mathbb{C}$} | {$\cong M_8(\mathbb{C})$} |
If both {$p$} and {$q$} are nonzero, then set {$r=\textrm{min}(p,q)$} and tensor {$r$} copies of {$M_2(\mathbb{R})$} to the Clifford algebra {$\textrm{Cl}_{p-r,q-r}(\mathbf{R})$}.
See also:  Classification of Clifford algebras
Classification of Clifford algebras
Symmetric spaces
How do the groups {$A_k=M(C_k)/i^*(M(C_{k+1}))$} relate to John Baez's forgetful functor by which he defines symmetric spaces?
Topological insulators
Superalgebras
Complex spin representations
Real spin representations
Homotopy groups
Notes