• View
• Edit
• History
• Print

Research Program Fivesome

I want to understand how to interpret combinatorially the equation for Sheffer polynomials

{$$\sum_{n=0}^{\infty}S_n(x)t^n=A(t)e^{xu(t)} \hspace{40 mm}(1)$$}

where, additionally, {$\{S_n(x)\}$} are orthogonal polynomials or closely related to orthogonal polynomials.

I know how to interpret the Sheffer polynomials in equation {$(1)$} as space builders. However, I am having trouble specializing that to the case of orthogonal Sheffer polynomials. I am trying to investigate that in various ways. I need to relate {$(1)$} and {$(2)$}.

{$$P_{n+1}(x) = (x - (nl + f)) P_n(x) - n(nk + c) P_{n-1}(x) \hspace{40 mm}(2)$$}

Show that we should define

{$$\sum_{n=0}^{\infty}\frac{1}{n!}P_n(x)t^n = \sum_{n=0}^{\infty}S_n(x)t^n=A(t)e^{xu(t)} $$}

Note that we need {$u_0=0$} because that is what makes {$P_n(x)$} a polynomial of degree {$n$}. Otherwise {$P_0(x)$} is an infinite series in {$x$}.

{$A(t)e^{xu(t)} = \sum_{n=0}^{\infty}S_n(x)t^n = \sum_{n=0}^{\infty}\frac{1}{n!}P_n(x)t^n$}

{$=(a_0+a_1t+a_2t^2+...)e^{x(u_1t+u_2t^2+...)}$}

{$=(a_0+a_1t+a_2t^2+...)(1+x(u_1t+u_2t^2+...) + \frac{1}{2!}x^2(u_1t+u_2t^2+...)^2 + \frac{1}{3!}x^2(u_1t+u_2t^2+...)^3 + ... $}

The leading term for {$P_n(x)$} is given by {$\frac{a_0u_1^nx^nt^n}{n!}$} as {$\frac{a_0u_1^n}{n!}$}.

For the polynomials {$P_n(x)$} to be monic, we need {$a_0u_1^n=1$} for all {$n$}.

Thus {$a_0=1$} and {$u_1=1$}.

And we see that {$S_n(x)$} can't be monic because of the factor {$\frac{1}{n!}$}.

One way to proceed is to focus on the generating functions for special cases, starting with the Hermite polynomials, which are the simplest case.

Probabilists's Hermite polynomials {$\{He_n(x)\}$}

{$ \sum_{n=0}^\infty \frac{He_n(x)}{n!} t^n = e^{-\frac12 t^2}e^{xt} = (1 - \frac{1}{1!\cdot 2}t^2 + \frac{1}{2!\cdot 2^2}t^4 - \frac{1}{3!\cdot 2^3}t^6 + \frac{1}{4!\cdot 2^4}t^8 - \dots )e^{xt} $}

{$ \mathit{He}_{n+1}(x) = x\mathit{He}_n(x) - n\mathit{He}_{n-1}(x) $}

This recurrence relation is a specialization of the general case with {$l=0, f=0, k=0$} and {$c=-1$}.

We can multiply out the generating functions

{$ \sum_{n=0}^\infty \frac{He_n(x)}{n!} t^n = (1 - \frac{1}{1!\cdot 2}t^2 + \frac{1}{2!\cdot 2^2}t^4 - \frac{1}{3!\cdot 2^3}t^6 + \frac{1}{4!\cdot 2^4}t^8 - \dots )(1+xt+\frac{1}{2!}x^2t^2 +\frac{1}{3!}x^3t^3 + \dots )$}

to get the explicit formula for the {$(n-2k)$} th term of {$He_n(x)$}, where {$⌈\frac{n}{2}⌉\leq k\leq n$}

{$\frac{(-1)^k}{2^k} \binom{n-k}{k} n(n-1)\cdots(n-(k-1))x^{n-2k} $}

which we can interpret combinatorially. Given labels {$\{1,\dots,n\}$}, we choose {$k$} pairs and {$n-2k$} singletons. To do this, first we choose {$k$} labels that we explicitly assign as elements in the pairs {$(p_1,\dots,p_k)$}. There are {$n(n-1)\dots (n-(k-1))$} ways to do this. Then, we are left with {$n-k$} labels, and from them we choose {$n-2k$} singletons and {$k$} implicitly assigned elements for the pairs {$(p_1,\dots,p_k)$}. We assign a weight {$\frac 12$} to each pair to address the fact that we have double counted them. Furthermore, we assign a weight {$-1$} to each pair and a weight {$x$} to each singleton.

It is interesting how the notion of choice (as in probability) arises here, and especially, how it gets assembled from three different sources (three factorials). This may give a clue as to how the divisions of everything manifest choice and probability.

Note that the objects grow much as the Sheffer polynomials interpreted as space builders. However, {$u(t)=t$}, {$u'(t)=1$} and {$u''(t)=0$}. Thus each compartment {$x$} is associated with exactly one label.

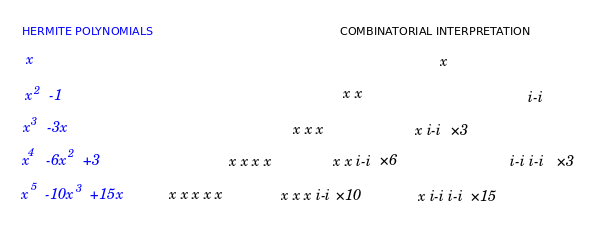
We see that {$A(t)$} contributes building blocks that are pairs with weight {$-1$} because of the quadratic power {$-\frac{1}{2}t^2$} which also includes the fraction {$\frac 12$} which handles the double counting of the pairs. Whereas {$u(t)$} contributes building blocks that are singletons with weight {$x$} because of the linear power {$xt$}. Three factorials come together to yield {$n(n-1)\dots (n-(k-1))\binom{n-k}{k}$} where the initial term {$n(n-1)\dots (n-(k-1))$} generates the explicitly assigned elements of the pairs and the binomial coefficient {$\binom{n-k}{k}$} yields {$k$} implicitly assigned elements of the pairs. Thus each pair consists of an explicitly assigned element and an implicitly assigned element. The explicitly assigned element was determined by choosing sequentially, so that the choices are ordered but not the labels, whereas the implicitly assigned element was determined by choosing collectively and then ordering the elements to determine the pairs they belong to.

We also see that the recurrence relation can be interpreted straightforwardly. Given labels {$\{1,\cdots,n\}$}, if we add a new label {$n+1$}, then we can add a new singleton with weight {$x$} or we can add a new pair with weight {$-1$} in {$n$} possible ways.

Explain how the objects (the combinations) arise by adding singletons x and converting them into pairs x => i-i or inserting them in between pairs i-i => i-x-i, thus yielding all possible combinations of pairs and singletons.

What is the source of the minus sign {$-1$} ?

Physicists's Hermite polynomials {$\{H_n(x)\}$}

{$ \sum_{n=0}^\infty \frac{H_n(x)}{n!} t^n = e^{-t^2}e^{x\cdot 2t} = (1 - \frac{1}{1!}t^2 + \frac{1}{2!}t^4 - \frac{1}{3!}t^6 + \frac{1}{4!}t^8 - \dots )e^{x\cdot 2t} $}

{$ H_{n+1}(x) = 2xH_n(x) - 2nH_{n-1}(x) $}

The recurrence relation is not monic in {$x$} and so does not have the general form.

We can relate them to the probabilists's Hermite polynomials by rescaling:

{$H_n(x)=2^{\frac{n}{2}}He_n(\sqrt{2}x)$}

{$He_n(x)=\frac{1}{2^{\frac{n}{2}}}H_n(\frac{x}{\sqrt{2}})$}