Introduction E9F5FC

Questions FFFFC0

• View
• Edit
• History
• Print

Clifford algebras, Clifford modules

{$\mathbb{Z}_2$}-Graded Modules

Dale Husemoller. Fiber Bundles. Chapter 12. Clifford Algebras.

A {$\mathbb{Z}_2$}-graded module {$M$} over a {$\mathbb{Z}_2$}-graded algebra {$A$} is an {$A$}-module {$M$} with {$M=M^0\oplus M^1$} such that {$A^iM^j\subset M^{i+j}$} for {$i,j\in\mathbb{Z}_2$}. Thus we have even maps even to even; even maps odd to odd; odd maps even to odd; odd maps odd to even.

We can write out the basis so that we can see from the quadrants of the matrices that the module is {$\mathbb{Z}_2$}-graded. Matrices for even elements should have blocks on the diagonal. Matrices for odd elements should have blocks on the antidiagonal.

{$\mathbb{R}$}

The algebra {$\mathbb{R}$} has no generator. It is completely even. It has no odd component.

Consider the two-dimensional {$\mathbb{R}$}-module with operation

{$x\Leftrightarrow \begin{pmatrix} x & 0 \\ 0 & 0 \end{pmatrix}$}

Does this satisfy the requirements? Is this a {$\mathbb{Z}_2$}-graded module?

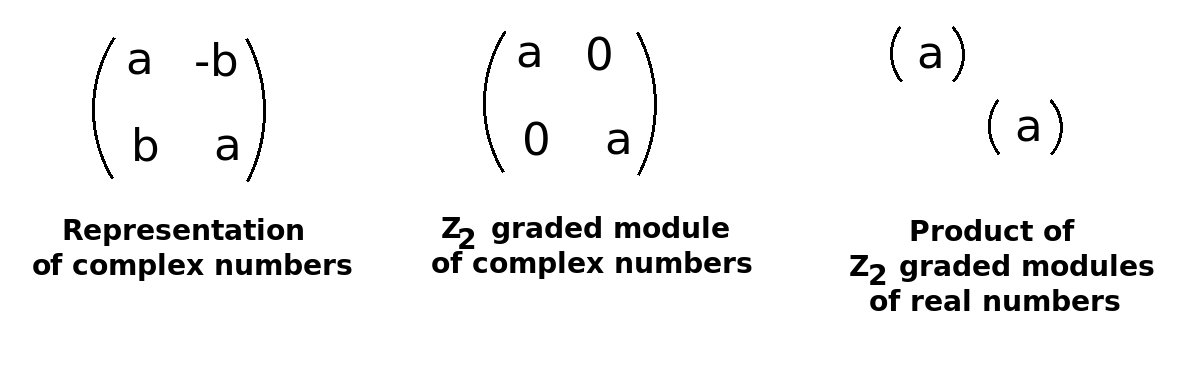
{$\mathbb{C}$}

Consider the simple two-dimensional {$\mathbb{C}$}-module with operation

{$x+ye_1\Leftrightarrow \begin{pmatrix} x & -y \\ y & x \end{pmatrix}$}

Note that this is a {$\mathbb{Z}_2$}-graded module because

{$\begin{pmatrix} x & 0 \\ 0 & x \end{pmatrix}\begin{pmatrix} u \\ v\end{pmatrix}=\begin{pmatrix} xu \\ xv\end{pmatrix}$}

{$\begin{pmatrix} 0 & -y \\ y & 0 \end{pmatrix}\begin{pmatrix} u \\ v\end{pmatrix}=\begin{pmatrix} -yv \\ xu\end{pmatrix}$}