- MathNotebook
- MathConcepts
- StudyMath
- Geometry
- Logic
- Bott periodicity
- CategoryTheory
- FieldWithOneElement
- MathDiscovery
- Math Connections
Epistemology
- m a t h 4 w i s d o m - g m a i l
- +370 607 27 665
- My work is in the Public Domain for all to share freely.
- 读物 书 影片 维基百科
Introduction E9F5FC
Questions FFFFC0
Software
Split-Complex Numbers
As Clifford Algebra, Direct Sum and Matrix Algebra
Will relate
- Split-complex numbers {$x+yj$} where {$j^2=1$}
- Clifford algebra {$x+y\epsilon_1\in Cl_{1,0}(\mathbb{R})$} where {$\epsilon_1^2=1$}
- Direct sum {$(a,b)\in\mathbb{R}\oplus\mathbb{R}$}
- Matrix algebra
{$\begin{pmatrix} x & y\\ y & x \end{pmatrix}$}
{$\begin{pmatrix} x+y & 0\\ 0 & x-y \end{pmatrix} = \begin{pmatrix} a & 0\\ 0 & b \end{pmatrix}$}
{$\begin{pmatrix} \frac{a}{2} & \frac{a}{2} & 0 & 0 \\ \frac{a}{2} & \frac{a}{2} & 0 & 0 \\ 0 & 0 & \frac{b}{2} & \frac{-b}{2} \\ 0 & 0 & \frac{-b}{2} & \frac{b}{2} \end{pmatrix}$}
Starting point
Real numbers {$x\in\mathbb{R}$} are a  field.
field.
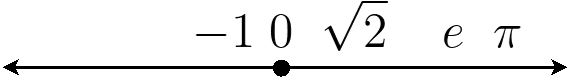
Question: What are dimensions? What is the relationship between dimensions?
How to extend the real numbers? {$x\in\mathbb{R}^n$} dimension {$n$} Vector!
Focus on two dimensions. {$(x_1,y_1)+(x_2,y_2)=(x_1+x_2,y_1+y_2)$}
Vector addition is straightforward. Group which is commutative, abelian.
Example: Answer is amount and unit. Add like units.
Multiplying vector by a scalar is straightforward. Scaling. Vector space
Multiply answer by amount.
{$\lambda(x_1,y_1) = (\lambda x_1,\lambda y_1)$}
Multiplying vectors becomes interesting! ring or algebra
What does it mean to multiply units?
{$(x_1,y_1)(x_2,y_2)=?$}
Definition
 Split-complex number {$z=x+yj$} where {$x,y\in\mathbb{R}$} and hyperbolic unit {$j^2=1$}
Split-complex number {$z=x+yj$} where {$x,y\in\mathbb{R}$} and hyperbolic unit {$j^2=1$}See the  synonyms.
synonyms.
We can also write {$z=x+yj$} as {$z=x+jy$}. We can think of it as {$z=x\mathbf{1}+y\mathbf{j}$}.
Compare with...
Complex numbers {$z=x+yi$} where {$x,y\in\mathbb{R}$} and imaginary unit {$i^2=-1$}
Dual numbers {$z=x+y\varepsilon$} where {$x,y\in\mathbb{R}$} and {$\varepsilon^2=0$} with {$\varepsilon\neq 0$}
Compare with... 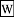 Split-quaternions {$Cl_{1,1}(\mathbb{R})\cong M_2(\mathbb{R})$}, Split-octonions, Split-biquaternions {$Cl_{0,3}(\mathbb{R})\cong \mathbb{H}\oplus\mathbb{H}$}
Split-quaternions {$Cl_{1,1}(\mathbb{R})\cong M_2(\mathbb{R})$}, Split-octonions, Split-biquaternions {$Cl_{0,3}(\mathbb{R})\cong \mathbb{H}\oplus\mathbb{H}$}
Geometry
Compare split-complex numbers multiplication by j (reflection), complex numbers multiplication by i (rotation), dual numbers multiplication by {$\varepsilon$} (rotation and projection). In each case, given point (a,b), the a rotates 90 degrees but the b rotates 90, -90 or 0, accordingly. Split-complex numbers change the definition of a and b by swapping them.
Goal
Philosophical question: How does the mind add one or more mathematical dimensions? mental perspectives? choices?
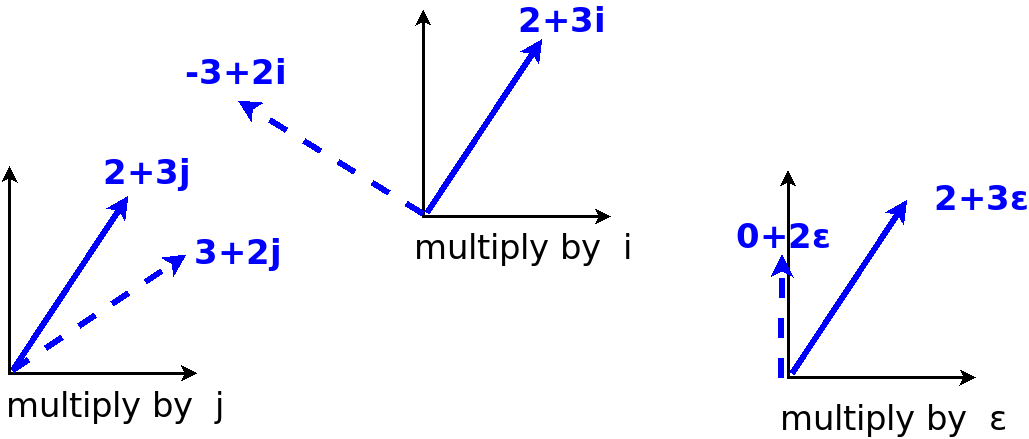
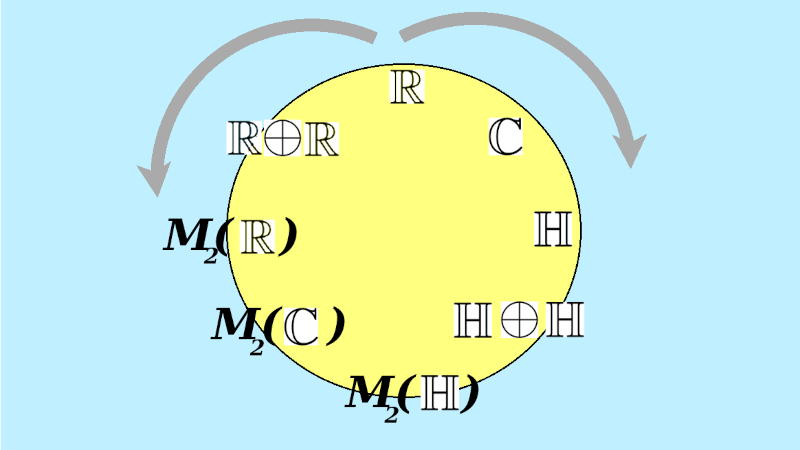
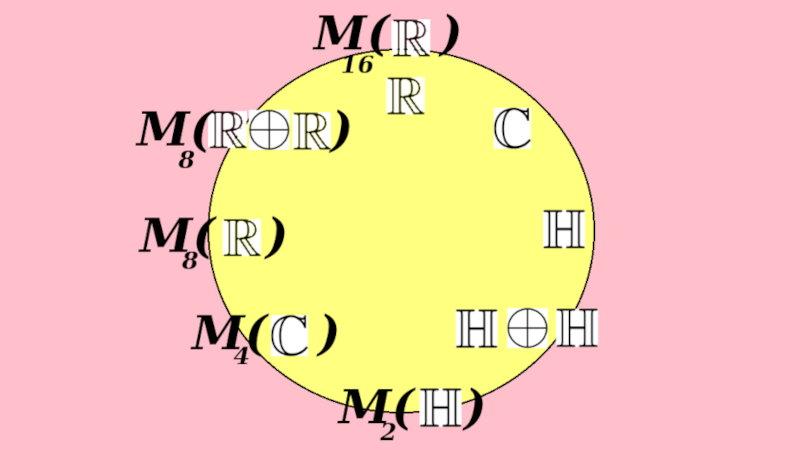
Challenge: Understand Bott periodicity!
We want to go back and forth between three ways of looking at this:
- Clifford algebras
- division algebras
- matrix algebras
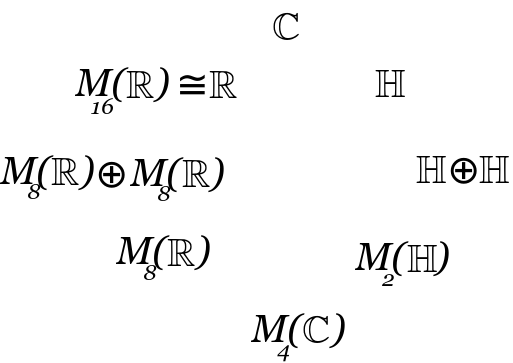
- {$\textrm{Cl}_{p+2,q}(\mathbf{R}) = \mathrm{M}_2(\mathbf{R})\otimes \textrm{Cl}_{q,p}(\mathbf{R}) $}
- {$\textrm{Cl}_{p+1,q+1}(\mathbf{R}) = \mathrm{M}_2(\mathbf{R})\otimes \textrm{Cl}_{p,q}(\mathbf{R}) $}
- {$\textrm{Cl}_{p,q+2}(\mathbf{R}) = \mathbf{H}\otimes \textrm{Cl}_{q,p}(\mathbf{R}) $}
Dale Husemoller. Fiber Bundles.
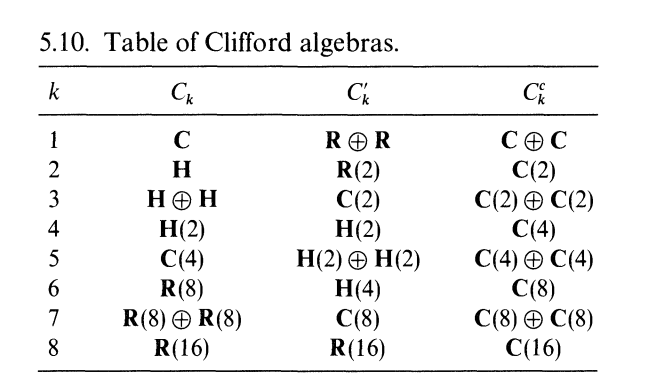

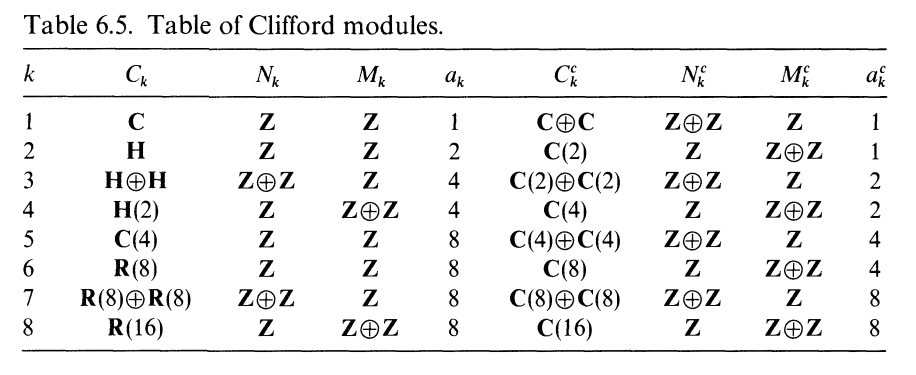
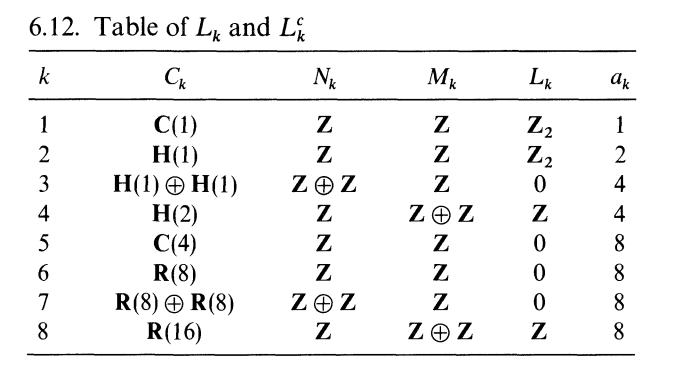
Clifford Algebra {$Cl_{1,0}(\mathbb{R})$}
All three number systems can be thought of as Clifford algebras.
Dual numbers are an  exterior algebra
exterior algebra
Express with matrices:
{$\epsilon_1 (u + v\epsilon_1)= (v + u\epsilon_1)$}
{$\begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix} \begin{pmatrix} u \\ v \end{pmatrix} = \begin{pmatrix} v \\ u \end{pmatrix}$}
{$1(u + v\epsilon_1)= (u + v\epsilon_1)$}
{$\begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix} \begin{pmatrix} u \\ v \end{pmatrix} = \begin{pmatrix} u \\ v \end{pmatrix}$}
Putting this together
{$(x + y\epsilon_1)(u + v\epsilon_1)= (xu + yv) + (xv + yu)\epsilon_1$}
{$\begin{pmatrix} x & y \\ y & x \end{pmatrix} \begin{pmatrix} u \\ v \end{pmatrix} = \begin{pmatrix} xu + yv \\ xv + yu \end{pmatrix}$}
How do we know whether this is the only matrix expression? And how do we find all the others?
Direct Sum: {$\mathbb{R}\oplus\mathbb{R}$}
Direct Sum Example: [5 hours + 43 minutes] + [2 hours + 12 minutes] = [7 hours + 55 minutes]
{$(a,b)+(c,d)=(a+c,b+d)$}
Zero looks like {$(0,0)$} as in {$(a,b)+(0,0)=(a,b)$}
Multiplication by a scalar
{$\lambda (a,b)=(\lambda a, \lambda b)$}
With product defined this way, this  direct sum is actually a product in category theory.
direct sum is actually a product in category theory.
{$(a,b)(c,d)=(ac,bd)$}
Identity looks like {$(1,1)$} as in {$(a,b)(1,1)=(a,b)=(1,1)(a,b)$}
Simple modules of {$\mathbb{R}\oplus\mathbb{R}$}
{$\mathbb{R}\oplus\mathbb{R}$} has two simple modules, {$C_1$} and {$C_2$}.
{$C_1$} has generator {$c_1$} where {$(a,b) \cdot c_1 = ac_1$}
{$C_2$} has generator {$c_2$} where {$(a,b) \cdot c_2 = bc_2$}
Thank you to John Baez at the Category Zulip Chat!
We need to show that these are abelian groups and that they satisfy the rules for modules, namely, given {$(a_1,b_1),(a_2,b_2)\in\mathbb{R}\oplus\mathbb{R}$} and {$m_1,m_2\in M$}, we have:
- {$(a_1,b_1)\cdot [m_1 + m_2] = (a_1,b_1)\cdot m_1 + (a_1,b_1)\cdot m_2$}
- {$[(a_1,b_1) + (a_2,b_2)]\cdot m_1 = (a_1,b_1)\cdot m_1 + (a_2,b_2)\cdot m_1$}
- {$[(a_1,b_1)(a_2,b_2)]\cdot m_1 = (a_1,b_1)\cdot [(a_2,b_2) \cdot m_1]$}
- {$(1,1)\cdot m_1=m_1$}
We want to show that every element of {$C_1$} has the form {$rc_1$}, where {$r\in\mathbb{R}$}, and likewise, every element of {$C_2$} has the form {$rc_2$}. Note that given two elements {$r_1c_1$} and {$r_2c_1$}, addition and scalar multiplication likewise yield elements of that form.
For example, for the module {$(a,b) \cdot c = ac$} we have:
- {$(a_1,b_1)\cdot [m_1 + m_2] = a_1(m_1+m_2) = a_1m_1 + a_1m_2 = (a_1,b_1)\cdot m_1 + (a_1,b_1)\cdot m_2$}
- {$[(a_1,b_1) + (a_2,b_2)]\cdot m_1 = (a_1+a_2,b_1+b_2)\cdot m_1 = (a_1 + a_2)m_1 = a_1m_1 + a_2m_1 = (a_1,b_1)\cdot m_1 + (a_2,b_2)\cdot m_1$}
- {$[(a_1,b_1)(a_2,b_2)]\cdot m_1 = (a_1a_2,b_1b_2)\cdot m_1 = (a_1a_2)m_1 = a_1(a_2m_1)= a_1 [(a_2,b_2) \cdot m_1 = (a_1,b_1)\cdot [(a_2,b_2) \cdot m_1]$}
- {$(1,1)\cdot m_1=1 m_1=m_1$}
Since every element has the form {$rc_1$}, it is straightforward to show they satisfy the rules for abelian groups, with the zero element {$0=0c_1$}, inverses {$-rc_1$}, well-definedness of {$r_1c_1 + r_2c_1 = (r_1+r_2)c_1$}, the associative rule {$r_1c_1+(r_2c_1 + r_3c_1)=(r_1c_1+r_2c_1)+r_3c_1$} and commutativity {$r_1c_1 + r_2c_1 = r_2c_1 + r_1c_1$}. This for {$C_1$} and similarly for {$C_2$}.
Note that these modules are simple. For example, suppose {$C_1$} had a nontrivial submodule {$D$}. Then there would have to be elements {$r_1c_1\in D, r_2c_1\notin D$}. But {$r_2c_1=\frac{r_2}{r_1}r_1c_1\in D$} with a contradiction.
And these two are nonisomorphic, thus distinct. For suppose there was an isomorphism {$f:C_1\rightarrow C_2$}. Then {$f((a,b)\cdot m)=(a,b)\cdot f(m)$}, thus {$f(am)=bf(m)$} for all {$a,b$}, namely, {$f(am)=0$} for all {$a\in\mathbb{R}$}, which is not an isomorphism.
These are the only simple {$\mathbb{R}\oplus\mathbb{R}$}-modules, up to isomorphism. For if there was another simple module {$M$}, then consider {$m\in M, m\neq 0$}. We have {$m = (1,1)\cdot m = (1,0)\cdot m + (0,1)\cdot m$}. At least one of the latter terms must be nonzero. Suppose it is {$(1,0)\cdot m$}. Then we have a submodule given by {$\{(a,0)\cdot m \;|\; a\in\mathbb{R}\}$} which is isomorphic to {$C_1$}. {$M$} is simple and so it must be equal to this submodule. But then {$M$} is isomorphic to {$C_1$} or otherwise {$C_2$}.
Isomorphism {$Cl(\mathbb{R})_{1,0}\cong \mathbb{R}\oplus\mathbb{R}$}
Compare {$(a,b)\in \mathbb{R}\oplus\mathbb{R}$} with {$x+y\epsilon_1\in Cl(\mathbb{R})_{1,0}$}.
{$(1,1)\Leftrightarrow 1$}
{$(1,-1)\Leftrightarrow \epsilon_1$}
{$(1,0)=\frac{1}{2}[(1,1)+(1,-1)]\Leftrightarrow\frac{1}{2}[1+\epsilon_1] $}
{$(0,1)=\frac{1}{2}[(1,1)-(1,-1)]\Leftrightarrow\frac{1}{2}[1-\epsilon_1]$}
{$(a,0)\Leftrightarrow\frac{a}{2}[1+\epsilon_1]$}
{$(0,b)\Leftrightarrow\frac{b}{2}[1-\epsilon_1]$}
{$(a,b)\Leftrightarrow\frac{a+b}{2}+\frac{a-b}{2}\epsilon_1$}
{$(a,b)\Leftrightarrow x+y\epsilon_1$}
{$x=\frac{a+b}{2}, y=\frac{a-b}{2}$}
{$a=x+y,b=x-y$}
{$(x+y,x-y)\Leftrightarrow x+y\epsilon_1$}
Decomposability
Why are split-complex number decomposable? Whereas complex numbers are not?
The  determinant of a matrix is the product of the eigenvalues:
determinant of a matrix is the product of the eigenvalues:
| Split-complex numbers | Complex numbers | Dual numbers |
| {$M=\begin{pmatrix} x & y \\ y & x \end{pmatrix}$} | {$M=\begin{pmatrix} x & -y \\ y & x \end{pmatrix}$} | {$M=\begin{pmatrix} x & 0 \\ y & x \end{pmatrix}$} |
| {$\textrm{det}(M)=x^2-y^2=(x-y)(x+y)$} | {$\textrm{det}(M)=x^2+y^2=(x-iy)(x+iy)$} | {$\textrm{det}(M)=x^2$} |
We can directly solve for the eigenvalues and eigenvectors:
{$M=\begin{pmatrix} x & y \\ y & x \end{pmatrix}\begin{pmatrix} v_1 \\ v_2 \end{pmatrix} = \lambda\begin{pmatrix} v_1 \\ v_2 \end{pmatrix}$}
{$xv_1+yv_2=\lambda v_1$}, {$yv_1+xv_2=\lambda v_2$}
| {$v_2=\frac{1}{y}(\lambda - x)v_1$} | {$v_1=\frac{1}{y}(\lambda - x)v_2=\frac{1}{y^2}(\lambda - x)^2v_1$} | {$\frac{(\lambda -x)^2}{y^2}=1$} | {$(\lambda -x)^2=y^2$} | {$\lambda - x = \pm y$} | {$\lambda = x+y$} or {$\lambda = x-y$} |
We can express {$M=SM'S^{-1}$} whereby {$M$} and {$M'$} are related by a change of bases. We can solve for {$S$} by writing {$MS=SM'$}. This yields:
{$\begin{pmatrix} x & y \\ y & x \end{pmatrix} = \begin{pmatrix} s & t \\ s & -t \end{pmatrix}\begin{pmatrix} x+y & 0 \\ 0 & x-y \end{pmatrix}\begin{pmatrix} \frac{1}{2s} & \frac{1}{2s} \\ \frac{1}{2t} & \frac{-1}{2t} \end{pmatrix}$}
Matrix Algebra
{$\begin{pmatrix} x & y \\ y & x \end{pmatrix}$}
Rewritten with {$x=\frac{a+b}{2}$}, {$y=\frac{a-b}{2}$} where {$(a,b)\in\mathbb{R}\oplus\mathbb{R}$}. This yields:
{$ \begin{pmatrix} \frac{a+b}{2} & \frac{a-b}{2} \\ \frac{a-b}{2} & \frac{a+b}{2} \end{pmatrix} + \begin{pmatrix} \frac{c+d}{2} & \frac{c-d}{2} \\ \frac{c-d}{2} & \frac{c+d}{2} \end{pmatrix} = \begin{pmatrix} \frac{a+b+c+d}{2} & \frac{a+c-b-d}{2} \\ \frac{a+c-b-d}{2} & \frac{a+b+c+d}{2} \end{pmatrix} $}
{$ \begin{pmatrix} \frac{a+b}{2} & \frac{a-b}{2} \\ \frac{a-b}{2} & \frac{a+b}{2} \end{pmatrix} \begin{pmatrix} \frac{c+d}{2} & \frac{c-d}{2} \\ \frac{c-d}{2} & \frac{c+d}{2} \end{pmatrix} = \begin{pmatrix} \frac{ac+bd}{2} & \frac{ac-bd}{2} \\ \frac{ac-bd}{2} & \frac{ac+bd}{2} \end{pmatrix} $}
because {$\frac{(a+b)(c+d) + (a-b)(c-d)}{2\cdot 2}=\frac{(ac+ac) + (ad-ad) + (bc-bc) + (bd+bd)}{2\cdot 2}=\frac{2ac+2bd}{2\cdot 2}=\frac{ac+bd}{2}$}
likewise {$\frac{(a+b)(c-d) + (a-b)(c+d)}{2\cdot 2}=\frac{(ac+ac) + (ad-ad) + (bc-bc) + (-bd-bd)}{2\cdot 2}=\frac{2ac-2bd}{2\cdot 2}=\frac{ac-bd}{2}$}
Taking projections
Given {$(a,b)\in\mathbb{R}\oplus\mathbb{R}$} we can set {$b=0$}, yielding the left projection {$(a,0)$}, and we can set {$a=0$}, yielding the right projection {$(0,b)$}.
Representation based on left projection
{$ \begin{pmatrix} \frac{a}{2} & \frac{a}{2} \\ \frac{a}{2} & \frac{a}{2} \end{pmatrix} + \begin{pmatrix} \frac{c}{2} & \frac{c}{2} \\ \frac{c}{2} & \frac{c}{2} \end{pmatrix} = \begin{pmatrix} \frac{a+c}{2} & \frac{a+c}{2} \\ \frac{a+c}{2} & \frac{a+c}{2} \end{pmatrix} $}
{$ \begin{pmatrix} \frac{a}{2} & \frac{a}{2} \\ \frac{a}{2} & \frac{a}{2} \end{pmatrix} \begin{pmatrix} \frac{c}{2} & \frac{c}{2} \\ \frac{c}{2} & \frac{c}{2} \end{pmatrix} = \begin{pmatrix} \frac{ac}{2} & \frac{ac}{2} \\ \frac{ac}{2} & \frac{ac}{2} \end{pmatrix} $} because {$\frac{ac}{4}+\frac{ac}{4}=\frac{ac}{2}$}
But we could have simply {$(a)$}.
Representation based on right projection
{$ \begin{pmatrix} \frac{b}{2} & \frac{-b}{2} \\ \frac{-b}{2} & \frac{b}{2} \end{pmatrix} + \begin{pmatrix} \frac{d}{2} & \frac{-d}{2} \\ \frac{-d}{2} & \frac{d}{2} \end{pmatrix} = \begin{pmatrix} \frac{b+d}{2} & \frac{-b-d}{2} \\ \frac{-b-d}{2} & \frac{b+d}{2} \end{pmatrix} $}
{$ \begin{pmatrix} \frac{b}{2} & \frac{-b}{2} \\ \frac{-b}{2} & \frac{b}{2} \end{pmatrix} \begin{pmatrix} \frac{d}{2} & \frac{-d}{2} \\ \frac{-d}{2} & \frac{d}{2} \end{pmatrix} = \begin{pmatrix} \frac{bd}{2} & \frac{-bd}{2} \\ \frac{-bd}{2} & \frac{bd}{2} \end{pmatrix} $} because {$\frac{bd}{4}+\frac{bd}{4}=\frac{bd}{2}$} and {$(-b)(d)=(b)(-d)=-bd$}
Can we make this one-dimensional?
{$(a,b),(c,d)\in\mathbb{R}\oplus\mathbb{R}$}
{$(a)(c)=(ac)$}
{$(b)(d)=(bd)$}
{$x+y\epsilon_1, u+v\epsilon_1\in Cl_{1,0}(\mathbb{R})$}
{$(x+y\epsilon_1)(u+v\epsilon_1)=xu+yv+(xv+yu)\epsilon_1$}
{$(x+y)(u+v)=xu+xv+yu+yv=([xu+yv]+[xv+yu])$}
{$(x-y\epsilon_1)(u-v\epsilon_1)=xu+yv-(xv+yu)\epsilon_1$}
{$(x-y)(u-v)=xu-xv-yu+yv=([xu+yv]-[xv+yu])$}
Further Study
Questions
How does this apply to the split biquaternions? {$\mathbb{H}\oplus\mathbb{H}$}
How do we make sense of the {$\mathbb{Z}_2$}-graded representations?
How do we calculate the group relevant for Bott periodicity?
What happens when we replace the real numbers with matrices of real numbers? {$M_8(\mathbb{R})\oplus M_8(\mathbb{R})$}
Why are 0, -1, 1 key for Clifford algebras?
