- MathNotebook
- MathConcepts
- StudyMath
- Geometry
- Logic
- Bott periodicity
- CategoryTheory
- FieldWithOneElement
- MathDiscovery
- Math Connections
Epistemology
- m a t h 4 w i s d o m - g m a i l
- +370 607 27 665
- My work is in the Public Domain for all to share freely.
- 读物 书 影片 维基百科
Introduction E9F5FC
Questions FFFFC0
Software
See: Bott periodicity
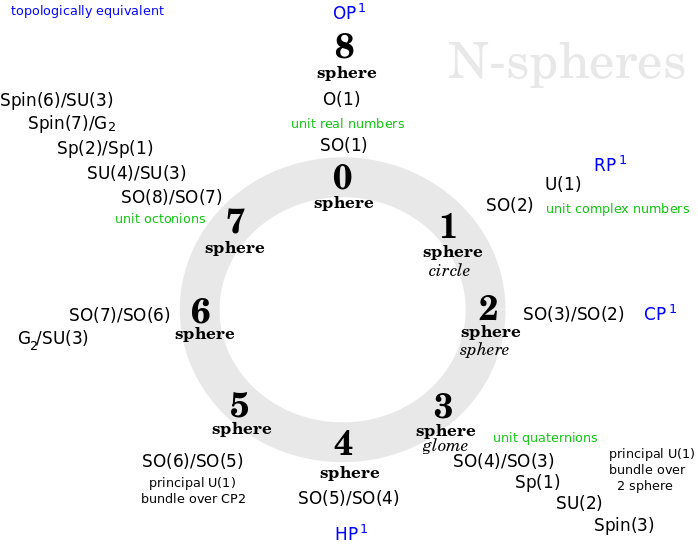
Investigation: Understand n-spheres and relate them to Bott periodicity and the divisions of everything.
- What is the significance (for Bott periodicity) of {$S^{n-1}=SO(n)/SO(n-1)$} ?
- Relate Bott periodicity with the n-spheres from the 0-sphere to the the 7-sphere (and 8-sphere).
- How can the fact that {$\Gamma(\frac{1}{2})=\sqrt{\pi}$} relate {$\pi$} and {$e$}? Note that {$\Gamma(1)=0!$} and {$\Gamma(\frac{3}{2})=\frac{\sqrt{\pi}}{2}$}. Consider the integral definition.
Sphere eversion
- How does sphere eversion work?
- Is sphere eversion related to the three-cycle?
- Is sphere eversion related to Bott periodicity?
trivial tangent bundles on spheres?
Bott periodicity relates to the homotopy groups of n-spheres.
Readings
- W: N-sphere
- W: Parallelizable manifold
- Agricola et al. On the history of the Hopf problem. Does {$S^6$} admit a complex structure?
- MSE: Bott periodicity and homotopy groups of spheres
- Bott, Hirzebruch. Bott periodicity and the parallelizability of the spheres.
- W: Exotic sphere
- W: H-space S0, S1, S3, S7 are the only spheres that are H-spaces.
- Arkadii Slinko. 1, 2, 4, 8,... What comes next? Parallelizability of spheres.
- Video animation 22 seconds
- Outside In 21 minutes
Facts
Stable homotopy group of spheres
- Barratt-Priddy-Quillen theorem. The group completion of the monoid of finite sets {$Fin^{gp}$} is the stable homotopy group of spheres.
- The volume of a unit sphere in n-dimensions goes up for small n, reaches a maximum at n=5, then goes down. https://en.wikipedia.org/wiki/Volume_of_an_n-ball
- Spheres make prominent the dimensions 0/1, 1/2, 3/4, 7/8 that accord with the normed division algebras. The divisions of everything likewise pair odd and even divisions but also include 5/6.
- Exotic sphere Kervaire-Milnor formula {$\Theta = \Pi B$} where {$B=a_m2^{2m-2}(2^{2m-1}-1)B_{2m}/4m$} for the order of the relevant cyclic subgroup.
- nLab: Sphere spectrum The sphere spectrum is the suspension spectrum of the point. The homotopy groups of the sphere spectrum are the stable homotopy groups of spheres. The sphere spectrum is the higher version of the ring Z of integers. See also: nLab: Suspension
Unit spheres
- John Baez. Octonions, normed division algebras and Bott periodicity. Clifford algebras {$Cl_{0,n}$}, whether they admit a representation on {$k$}-dimensional vector space, which is if and only if the unit sphere in that vector space {$S^{k-1}$}, admits {$n$} linearly independent smooth vector fields.
Max Karoubi. Algebraic maps between spheres and Bott periodicity.
- Related to Adams's work on vector fields on spheres.
- 6+4=2 modulo 8
Stable space
- The symmetry of Bott periodicity does not depend on the size of the dimensions but is deeper than whole numbers. If we think in terms of numbers, then it becomes much more complicated, as with the homotopy of spheres.