Introduction E9F5FC

Questions FFFFC0

• View
• Edit
• History
• Print

Consider a functor {$F:C\rightarrow\textrm{Set}$}.

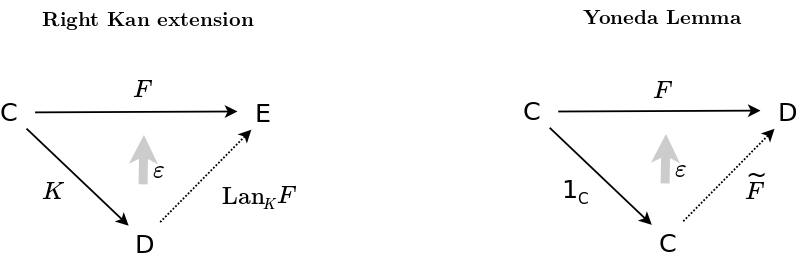
{$\tilde{F}\cong F$}

{$Fc \cong \textrm{lim}(c/C\overset{\Pi}\rightarrow C\overset{F}\rightarrow D)$}

{$Fc \cong \textrm{Set}(*,Fc)$}

This is simply rethinking the objects of {$Fc$} as arrows.

{$Fc$} is a set. And {$*$} is any singleton (any set with one element). {$\textrm{Set}(*,Fc)$} is the set of set functions from the singleton to the set {$Fc$}, which is to say, it is a set of arrows. Any such set function simply takes the singleton to some element of the set {$Fc$}. Thus the set {$\textrm{Set}(*,Fc)$} is in bijection with the set {$Fc$}.

But furthermore we can think of {$Fc$} as a functor with input {$c$} and we can think of {$\textrm{Set}(*,Fc)$} as a functor with input c. We can show that these two functors are naturally isomorphic by considering what they do to an arrow {$f:c\rightarrow c'$} in {$C$}.

{$Ff:Fc\rightarrow Fc'$} is a set function. And {$\textrm{Set}(*,Ff):\textrm{Set}(*,Fc)\rightarrow \textrm{Set}(*,Fc')$} is a set function which postcomposes the elements of {$\textrm{Set}(*,Fc)$} with the arrow {$f$} to get the elements of {$\textrm{Set}(*,Fc')$}. We can define a natural transformation {$\gamma$} with components {$\gamma_c: Fc\rightarrow \textrm{Set}(*,Fc)$} which sends each element in {$Fc$} to the set function which sends the singleton to {$Fc$}. This map is reversible and defines a natural isomorphism.

{$Fc \cong \textrm{Cone}(*,F\Pi)$}

This comes from applying {$Fc \cong \textrm{lim}(c/C\overset{\Pi}\rightarrow C\overset{F}\rightarrow D)$}

• which comes from {$\textrm{Ran}_KF(d):= \textrm{colim}(d\downarrow K\ \overset{\Pi^d} \rightarrow C \overset{F}\rightarrow E)$}
• where {$d\downarrow K$} is the category of elements of the functor {$D(d, K\_):C^{op}\rightarrow\textrm{Set}$} which comes with the canonical projector functor {$\Pi^d:d\downarrow K\rightarrow C$}.

The category of elements {$\textrm{el}(F$}) of the functor {$F:C\rightarrow\textrm{Set}$} is defined as follows:

• Objects are pairs {$(A,a)$} where {$A\in \mathop{\rm {Ob}} (C)$} and {$a\in FA$}.
• Morphisms {$\displaystyle (A,a)\to (B,b)$} are arrows {$f:A\to B$} such that {$(Ff)a=b$}.
• In other words, this is the comma category {$*\downarrow F$} where {$*$} is a singleton.
• The projection {$\Pi:\textrm{el}(C)\rightarrow C$} sends object {$(A,a)$} to {$A$} and sends morphism {$(A,a)\to (B,b)$} to {$f$}.

Given object {$d$} in {$D$} and functor {$K:C\rightarrow D$}, the category {$d\downarrow K$} of elements of the functor {$D(d,K\_):C^{op}\rightarrow\textrm{Set}$} is defined as follows:

• Objects are pairs {$(c,f)$} where {$c$} is an object in {$C$} and {$f$} is an element in the set of arrows {$D(d,Kc)$}.
• In other words, objects are pairs {$(c,f:d\rightarrow Kc)$}.
• Morphisms {$(c_1,f_1:d_1\rightarrow Kc)\to (c_2,f_2:d\rightarrow Kc)$} are arrows {$f:c_1\to c_2$} such that {$(D(d,K\_)f)f_1=f_2$}.
• Note that {$D(d,K\_)f:D(d,Kc_1)\rightarrow D(d,Kc_2)$} is postcomposition with {$Kf:Kc_1\rightarrow Kc_2$}.
• So {$(D(d,K\_)f)f_1 = f_2$} by postcomposition means that {$f_1\circ Kf = f_2$} by precomposition.
• The projection {$\Pi^d:d\downarrow K\rightarrow C$} sends object {$(c,f)$} to {$c$} and sends morphism {$(c_1,f_1)\to (c_2,f_2)$} to {$f$}.

Given object {$c$} in {$C$} and functor {$\textrm{Id}_C:C\rightarrow C$}, the category {$c\downarrow \textrm{Id}_C$} of elements of the functor {$C(c,\_):C^{op}\rightarrow\textrm{Set}$} is defined as follows:

• Objects are pairs {$(c',f:c\rightarrow c')$}
• Morphisms {$(c_1,f_1:c\rightarrow c_1)\to (c_2,f_2:c\rightarrow c_2)$} are arrows {$f:c_1\to c_2$} such that {$(C(c,\_)f)f_1=f_2$}.
• And {$(C(c,\_)f)f_1=f_2$} means that {$f_1\circ f=f_2$} by composition.

This is the same as {$c/C$} where {$C$} is a category with an object {$c$}. This is the slice category of {$C$} under {$c$} (which is a special case of a comma category) defined as follows:

• The objects are the morphisms {$f:c\rightarrow x$}.
• A morphism from {$f:c\rightarrow x$} to {$g:c\rightarrow y$} is a map {$h:x\rightarrow y$} such that {$g=hf$}, which is to say, their triangle commutes.
• The projection {$\Pi:c/C\rightarrow C$} sends object {$f$} to {$x$} and sends morphism {$(f,x)\overset{h}\to (g,y)$} to {$h$}.

{$c/C\overset{\Pi}\rightarrow C\overset{F}\rightarrow D$} is a functor {$F\Pi$} from {$c/C$} to {$D$}

• An object {$f$} in {$c/C$} is a morphism {$f:c\rightarrow x$}.
• The projection functor {$\Pi$} sends {$f$} to {$x$}, and then {$x$} gets sent to {$Fx$}
• A morphism {$h:x\rightarrow y$} in {$c/C$} gets sent to {$h$}, and then {$h$} gets sent to {$Fh$}

For a diagram {$F:J\rightarrow C$}, the functor {$\textrm{Cone}(\_,F):C^{op}\rightarrow \textrm{Set}$} sends object {$c$} in {$C$} to the set of cones over {$F$} with summit {$c$}.

What is {$\textrm{Cone}(*,F\Pi)$}? Does {$*$} stand for {$c$}?

Marina Christina Lehner. “All Concepts are Kan Extensions”: Kan Extensions as the Most Universal of the Universal Constructions.