Introduction E9F5FC

Questions FFFFC0

• View
• Edit
• History
• Print

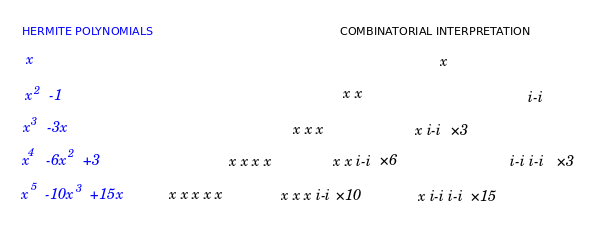
The probabilistic Hermite polynomial {$He_n(x)$} counts the following objects: {$n$} labeled vertices which may be linked into pairs, giving weight {$x$} to each unpaired vertex and weight {$i$} to each paired vertex. (Thus each pair contributes a weight {$-1$}.) This is a result in Viennot's general combinatorial theory of orthogonal polynomials and I learned of it from Drake's paper.

The physicist Hermite polnymoial {$H_n(x) = 2^{\frac{n}{2}}He_n(\sqrt{2x})$} is a rescaling. Combinatorially, it gives each unpaired vertex the weight {$2x$} and each paired vertex the weight {$\sqrt{2}i$}, which is to say, each pair gets weight {$-2$}.

The standard normal distribution and the probabilistic Hermite polynomials

The normal distribution {$N(\mu,\sigma^2)$} is the probability distribution over the reals with mean {$\mu$} and variance {$\sigma^2$} which has the maximum entropy. The standard normal distribution can be defined {$\phi(x)=N(0,1)=\frac{1}{\sqrt{2\pi}}e^{-\frac{1}{2}x^2}$}.

{$\sqrt{2\pi}\phi(x)=\frac{x^0}{2^00!}+\frac{x^2}{2^11!}+\frac{x^4}{2^22!}+\frac{x^6}{2^33!}+\frac{x^4}{2^44!}+\dots$}

This counts, for each {$n$}, the chance of choosing correctly from the number of ways of that {$n$} pairs of cells can be ordered, with a cell being chosen in each pair. And then assigning a weight {$ix$} to each cell.

The probabilistic Hermite polynomials {$He_n(x)$} figure in the {$n$}th derivative of the standard normal distribution {$\phi(x)$}:

{$\phi^{(n)}(x)=(-1)^nHe_n(x)\phi(x)$}

The Hermite polynomials counts involutions.

{$A(t)=e^{-\frac{1}{2}t^2}$}

{$A'(t)$} = {$-tA(t)$}

The value {$-t$} represents the beginning of a link. Differentiating {$A(t)$} yields the beginning of a link.

{$A''(t)$} = {$( -1 + t^2)A(t)$}

Differentiating {$t$} yields the ending of a link. It has weight {$+t^{-1}$}. The weight {$t^2$} means that there is a sequence of two links that have been started. It is a sequence because we have been generating this with a sequence of actions.

{$A'''(t) = [(-1 + t^2)(-t) + 2t]A(t) = (3t - t^3)A(t)$}

Taking the derivative of {$t^n$} yields {$nt^{n-1}$} and means that there are {$n$} open links and that we are closing any one of them. Taking the {$n$}th derivative of {$t^n$} means that given a sequence of {$n$} open links there are {$n!$} sequences by which they could all be closed.

{$A^{(4)}(t) = [(3t - t^3)(-t) + (3-3t^2)]A(t) = (3 -6t^2+t^4)A(t)$}

{$A^{(5)}(t) = [(3-6t^2+t^4)(-t) + (-12t + 4t^3)]A(t) = (-15t + 10t^3 - t^5)A(t)$}

The number of terms {$1,2,4,10,26,\dots$} is the number of involutions on {$n$} letters, equivalently, the number of standard Young tableaux with {$n$} cells. The power of {$t$} gives the number of fixed points.

{$\frac{\textrm{d}^n}{\textrm{dt}^n$}(\sum_{n=0}^{\infty}P_n(x)\frac{t^n}{n!}) = \frac{\textrm{d}^n}{\textrm{dt}^n$}(A(t)E(t))$}

I am looking for a bijection between involutions and Young tableaux. There is one based on the Robinson-Schensted-Knuth correspondence. Involutions correspond to those pairs {$(P,Ω)$} of standard tableaux such that {$P=Ω$}. This arises because involutions are permutations which are their own inverses.

Both objects satisfy the recurrence relations {$a_n=a_{n-1}+(n-1)a_{n-2}$}. This is straightforward for involutions. How does it work for standard tableaux? Given a standard tableaux with {$n-1$} cells, we add the cell {$n$} at the end of the 1st row. And given a standard tableaux {$X$} with {$n-2$} cells and a pair {$1\leq j<n$}, use the numbering {$1,\cdots,j-1,j+1,\cdots,n-1$} for the cells of {$X$}. We insert {$j$} using the Schensted action, as follows. In row 1, put j in the first cell {$y>j$} and if there is no such y, put j at the end of the row. If there was a y, then insert it in row 2 similarly. Go through the rows upwards until the action stops at row q. Then add the cell n to the end of the row q+1.

Janet Simpson Beisinger. Similar Constructions for Young Tableaux and Involutions, and Their Application to Shifted Tableaux

• Wikipedia: Hermite polynomials
• Wikipedia: Normal Distribution: Symmetries and derivatives
• Dan Drake. The Combinatorics of Associated Hermite Polynomials