Introduction E9F5FC

Questions FFFFC0

• View
• Edit
• History
• Print

Here I'm storing letters that I've received from a correspondent about his ideas on the Consistent Enumeration of Polytopes. Andrius

---

November 29, 2020

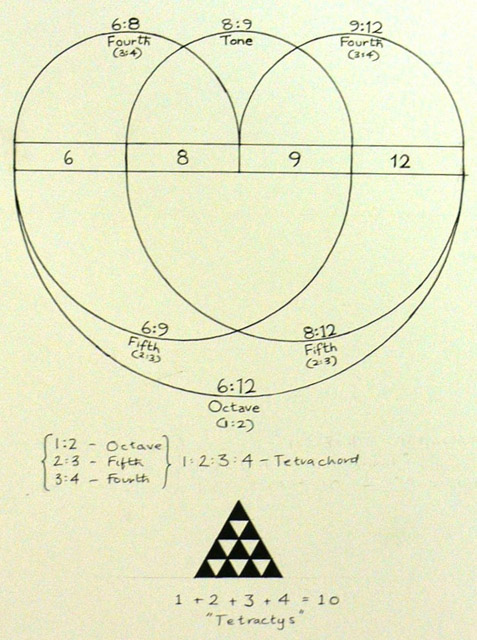
I suppose it is fine, but my name being present isn't ideal. If you showed that page to someone, they might be impressed that I have been sending you emails since 2002! Also to be clear, that nice hand-drawn picture at the bottom wasn't made by me. I found it with a search engine, so it may lead to confusion should that person be tracked down with a google image search or should anyone assume that I have advocated that definition of "tetrachord".

Is there some community you are sharing my emails with?

 The "projective point number" is 1.
 A "projective line number" is 1 + p.
 A "projective plane number" is 1 + p + p²
 A "projective space number" is 1 + p + p² + p³... etc.

Projective lines:

 1, 2, 3, 4, 5...

Projective planes:

 1, 7, 13, 21, 31...

Notice the consistent relationship between these projective numbers and n-cube numbers:

 0×1+1=1, 1×1+1=2, 3×1+1= 4,  7×1+1=  8
 0×1+1=1, 1×2+1=3, 4×2+1= 9, 13×2+1= 27
 0×1+1=1, 1×3+1=4, 5×3+1=16, 21×3+1= 64
 0×1+1=1, 1×4+1=5, 6×4+1=25, 31×4+1=125

Consider that the tetrahedron has 7 symmetry axes, cube/octahedron have 13 symmetry axes, and dodecahedron/icosahedron have 31 symmetry axes.

What if any relationship is there with the platonic solids and cube numbers? With polyhedra and cube numbers?

If an appropriate answer is given, then this should establish a consistent relationship between simplex and hypercube/cross-polytope triangles while also giving a unique triangle for the dodecahedron/icosahedron. This would be a very orderly universe, not just suitable for counting but also making explicit a relationship between music intervals and geometric objects.

First some observations on polygons and their diagonals:

 triangle - 1 convex triangle
 square   - 1 convex square, 1 pair of diagonal lines
 pentagon - 1 convex pentagon, 1 star pentagon
 hexagon  - 1 convex hexagon, 1 star hexagon, 1 triplet of diagonal lines
 heptagon - 1 convex heptagon, 2 star heptagons

...

Now consider that every star polygon has an image of the convex polygon inside it. (A star pentagon has a convex pentagon inside it. A star hexagon has a convex hexagon inside it...) The number of objects associated with an n-gon becomes n-2. (For example, a hexagon has 1 outer hexagon, 1 star hexagon, 1 triplet of lines, 1 inner hexagon, so the 6-gon has 4 objects associated with it. A heptagon has 1 outer heptagon, 2 star heptagons, 2 inner heptagons.)

I noticed that polygons made of intersecting circles capture this numerical relationship well, so I made some pictures and attached them to the email. These "circular polygons" have a round version of a polygon in the center and intersecting regions which look like flower petals. For example, 4 mutually intersecting circles to make a square formation has 4 layers: not intersecting layer,

 2 intersecting circles layer,
 3 intersecting circles layer,
 4 intersecting circles layer

The layers which have 2 and 3 intersections are the "flower petal layers".

The number of flower petals of an n-gon is n×(n-2):

 triangle - 3×1 =  3
 square   - 4×2 =  8
 pentagon - 5×3 = 15
 hexagon  - 6×4 = 24

(If the center is counted, the square numbers 4, 9, 16, 25... are achieved.)

Is this what should be counted or is it something else? hmm

Obviously, I'm not satisfied with polygons alone, so I modeled a tetrahedron made of spheres and attached pictures. The tetrahedron has 4 vertex-face lines and 3 edge-edge lines. The rest is a work in progress, but I should note that I have already noticed that this sphere intersection paradigm makes even the humble cube quite complicated with the simple tools I know which will model it.

I may or may not find what I'm looking for but the consistent relationship between the "projective numbers" and n-cube numbers is compelling enough to look for *something*.

November 23, 2020

My amateur investigations continue but now I am puzzling over new information. Pascal's triangle is one thing but the harmony of two triangles is another and the absence of the icosahedron and dodecahedron is frustrating. Is there no hope for the perfect union of number, geometry, and sound?

Well, it's possible this has been viewed through the wrong lens: vertices, edges, faces...

 1+2+4=7
 1+3+9=13
 1+5+25=31

These are the numbers of symmetry axes of the tetrahedron, cube, and dodecahedron respectively. In the below linked paper, the fano plane is described with 7 points using binary coordinates of the form (x,y,z). This means it can be seen as part of a 2x2x2 cube or multiplication table with the eighth or 0th part left implicit. (1+3+3+1 can also be seen as a cube as previously mentioned.) 4 axes are vertex to face axes. 3 axes are edge to edge. The eight "axis" can be the center or the object itself I suppose. This isn't strictly a tetrahedron but more abstract and cheaper than 4+6+4+1 vertex, edge, face, body parts.

Now consider the cube. A cube has 4 vertex to vertex axes, 6 edge to edge, 3 face to face. But is a cube just what's on the surface? In 2D, polygons are boring until the pentagon. The pentagon is the first to create itself within itself with its diagonals (a pentagram). A square doesn't create an inner square with its diagonals. In 3d, the cube creates an octahedron within itself by diagonal planes, but importantly, the tetrahedron doesn't create an inner tetrahedron. If 13 outer and 13 inner axes are counted, we get 26.

The dodecahedron is more complicated. There are 10 vertex to vertex axes, 15 edge to edge, 6 face to face. 5 cubes fit in a dodecahedron which make a rhombic triacontahedron at their intersection. These 5 cubes hold 5 tetrahedra 2 ways to allow 10 possible tetrahedra in the dodecahedron. 5 tetrahedron make an icosahedron at their intersection. 5 pairs of tetrahedra make 5 octahedra which trace out an icosidodecahedron at their intersection. This means there are 4 layers all having the same symmetry axes: dodecahedron, rhombic triacontahedron, icosidodecahedron, icosahedron.

10×4+15×4+6×4=124

7, 26, 124. Add 1 to each to get a 2x2x2, 3x3x3, and 5x5x5 cube.

http://archive.bridgesmathart.org/1998/bridges1998-121.pdf

"The first three primes p = 2, 3, and 5 therefore yield finite projective planes with 7, 13, and 31 points and lines, respectively. But these are just the numbers of symmetry axes of the five regular solids, as described in Plato's Timaeus: The tetrahedron has 4 pairs of face planes and comer points + 3 pairs of opposite edges, totaling 7 axes; the cube has 3 pairs of faces + 6 pairs of edges + 4 pairs of comers, totaling 13 axes (the octahedron simply interchanges the roles of faces and comers); and the pentagon dodecahedron has 6 pairs of faces + 15 pairs of edges + 10 pairs of comers, totaling 31 axes (the icosahedron again interchanging roles of faces and comers). This is such a suggestive result, one would expect to find it dealt with in most texts on related subjects; instead, while "well known to those who well know such things" (as Richard Guy likes to quip), it is scarcely to be found in the formal literature [9]. The reason for the common numbers, it turns out, is that the groups of symmetry motions of the regular solids are subgroups of the groups of collineations of the respective finite planes, a face axis being different from an edge axis of a regular solid but all points of a projective plane being alike, so the latter has more symmetries than the former."

September 8, 2002

What currently interests me is discovering the numbers of geometry and the numbers of music in the expectation that a comprehensive system will eventually be found which harmonizes them.

> The presentation you found is one that I hope to update later this year > or next. I need to think it through and write it up in more detail. > Also, the part about "demi-hypercubes" is not correct, and instead I > need to write about a different structure, what I call "coordinate > systems".

> Indeed, the "coordinate systems" are slices of a cube (1,3,3,1) or > slices of a tesseract (1,4,6,4,1) as you write. So this is the fourth > system that I was looking for, which has no center and no totality.

There is not a big difference between the two, but while you have shown (1,3,3,1) as a cube of 8 points, figurate number slices show 1 point, a 3 point triangle, another 3 point triangle, and another point. (Cube vs slices.)

If it interests you, I wish to share variations on the premise of Pascal's triangle.

1. Lists of f-vectors.
2. Diagrams of n-dimensional polytope figurate number slices.
3. Tables of n-dimensional polytope figurate numbers.
4. Pascal's pyramid and beyond.

Otherwise, skip to the part labeled "Section 5." This email accidentally got longer than necessary because I couldn't find the time to finish it in a single day and the more I came back the more I wanted to add.

1. Lists of f-vectors. (face-vectors) https://en.wikipedia.org/wiki/Polyhedral_combinatorics#Faces_and_face-counting_vectors This is the variation I initially saw you write about where (3, 3, 1) refers to 3 vertices, 3 edges, 1 triangle. But there is an important distinction between f-vectors of an abstract polytope and f-vectors as you have presented. I have no opinion on whether it is "right" or "wrong" but as I understand it a consistent presentation of polytope f-vectors would list all polytopes in the form (1, 3, 3, 1) or all in the form (3, 3, 1). This means a square would be (1, 4, 4, 1)---not (4, 4, 1)---if presented consistently alongside (1, 3, 3, 1). The longer form is the "complete" version where the 1s on each end represent the nullitope, or empty face, and maximal face. These ideas are from the modern theory of abstract polytopes. The proponents of which have their own ideas about the way to count shapes, but the abstract nature of numbers allows anyone to come up with new interpretations. I do not present them as authorities which you must not question. Instead I see a mystery regarding how to read these numbers.

2. Diagrams of figurate number slices. Since you aren't sure about the term "figurate numbers" I'll explain them:

 *  *    *      *
   * *  * *    * *
       * * *  * * *
             * * * *

Hopefully that rendered correctly. These are called triangular numbers. They are graphical representations of simple arithmetical series. The above represent 1, 3, 6, & 10, but it continues, 15, 21, 28, 36, 45, 55, etc... The earliest surviving detailed descriptions of figurate numbers are probably from Ancient Greece but they may have been known earlier in Babylonia. The classical figurate number arithmetic was recorded by Hypsicles who gave a version which makes symmetric figures for triangles and squares, and asymmetric depictions for pentagons and higher. https://en.wikipedia.org/wiki/Pentagonal_number https://en.wikipedia.org/wiki/Hypsicles http://wlym.com/archive/pedagogicals/polygonal.html

Today an alternative called "centered figurate numbers" exists which allows all figures to be symmetric. https://en.wikipedia.org/wiki/Centered_pentagonal_number

The Pythagoreans were known to study figurate numbers, and they held the fourth triangular number 10 to be of special importance, but their society was secretive and it's not clear what was so special about it. Later historical figures such as Plato and Nicomachus provide hints that there may have been a practice of mapping numbers to figurate number diagrams. An example of a "figurate number diagram" (my own term) is Pascal's triangle where the places which hold numbers can be is decided by a triangular number arrangement. The figurate number becomes a figurate number *diagram* when numbers are written in the slots.

Plato gives the following:

     1
   2  3
  4  6  9
 8 12 18 27

Except that later commentators provided 6, 12, & 18 Which makes a triangular number diagram. Nichomachus provides a multiplication table shown here by a square number diagram:

 1  2  3  4
 2  4  6  8
 3  6  9 12
 4  8 12 16

And a division table. Both Plato's diagram (on its rows) and the multiplication table (on its diagonals) have sums which give figurate numbers. Tetrahedral numbers are found on the sums of the multiplication table, and Plato's diagram sums to "nexus numbers" https://mathworld.wolfram.com/NexusNumber.html which is a surprising fact which seems to have gone unnoticed. Plato's triangle is a way to make ratios without fractions. His is based on 2:3. Triangles based on 1:2, 2:3, 3:4, 4:5, etc give the nexus numbers on their row sums. Plato's triangle and the division table are arithmetical approaches to making music intervals.

The reason I am explaining all this is to get back to Pascal's triangle and its variations. The standard Pascal diagram which gives hypercube slices is a triangle, but the next a square, and the next a pentagonal diagram, etc. Importantly, the pentagonal diagrams and further are *asymmetric* diagrams made with classical figurate numbers from antiquity, but they can also be displayed as isosceles triangles for simplicity. The slices of these hypercubes are figurate numbers themselves. The below diagram could be arranged as a square if wanted.

           1            = 1
         1 1 1          = 3
       1 2 3 2 1        = 9
     1 3 6 7 6 3 1      = 27
 1 4 10 16 19 16 10 4 1 = 81

On the row summing 27, 1 is a point, 3 is a triangular number, 6 is the next triangle, 7 is a centered hexagonal number. The next pascal-type slice diagram gives a cube of 64 points, and the next a cube of 125. https://mathworld.wolfram.com/CubicNumber.html

The diagrams of slices for the simplex and cross-polytope numbers do not grow the same way:

  1  = 1 point         1   = 1
 1 1 = 2 line         1 1  = 2
 1 2 = 3 triangle    1 2 1 = 4 square
 1 3 = 4 tetrahedron 1 4 1 = 6 octahedron
 1 4 = 5 5-cell      1 6 1 = 8 16-cell

I hypothesize that the Pythagoreans may have explored numerous diagrams and it is why they revered their triangular number of 10 because they kept learning new things by mapping numbers to it. https://en.wikipedia.org/wiki/Tetractys

Their oath:

    "By that pure, holy, four lettered name on high,
    nature's eternal fountain and supply,"

I'm not sure how it could be a fountain unless there was a practice of continual interaction, experimentation, and learning. I would not be surprised if they knew of Pascal's triangle, since it was known elsewhere in ancient times, but there is no evidence they did.

3. Tables of n-dimensional polytope figurate numbers. Pascal's triangle is a table of simplex numbers, so obvious alternatives are hypercube and cross-polytope tables:

 1  1  1   1   1
 1  2  3   4   5
 1  4  9  16  25
 1  8 27  64 125
 1 16 81 256 625

 1 1  1  1   1
 1 2  3  4   5
 1 4  9 16  25
 1 6 19 44  85
 1 8 33 96 225

https://oeis.org/A142978

I mention this not because these numbers should be especially significant---other than having satisfying graphical representations---but because they are obvious alternatives to Pascal's triangle.

4. Pascal's pyramid and beyond. The basic idea can be extended from the triangle to the tetrahedron, 5-cell, etc. https://en.wikipedia.org/wiki/Pascal%27s_pyramid

The sums of the triangles in the tetrahedron are 1, 3, 9, 27, 81... And you might guess the sums of the tetrahedron in the 5-cell are 1, 4, 16, 64, 256... Which are the same sums from the polygonal diagrams earlier. The main difference is the way the hypercubes are dissected. Layer 3 of the tetrahedron:

 1 3 3 1 = 8
  3 6 3 	= 12
   3 3   = 6
    1    = 1

(8, 12, 6, 1) is notable for being the f-vector of the cube, but what about 5-cell layers and beyond? If I remember correctly, they correspond with generalized hypercubes and cross-polytopes. https://en.wikipedia.org/wiki/Hypercube#Generalized_hypercubes https://en.wikipedia.org/wiki/Cross-polytope#Generalized_orthoplex https://en.wikipedia.org/wiki/Complex_polytope#Regular_complex_polytopes

These are called complex polytopes, but instead of calculating by triangles, one may wish to work algebraically by determining the coefficients of (x + m)^n, where Pascal's triangle is (x + 1)^n and n is the row number, while (x + 2)^n is the hypercube triangle.

Section 5. > I can refer you to a more recent one-page abstract that I wrote > http://www.ms.lt/derlius/KulikauskasAndrius-LNFK-43.pdf > where I do a better job of writing this up. Does it make sense?

I understand the binomial theorem analogy and why the simplex has been counted this way in this context but not why this is consistent with the counting of hypercube elements. In particular, I see why you would count a triangle as 8 elements instead of 7, but not why you would *consistently* count a cube as 27 instead of 28 elements at the same time other than convenient connection to number triangles unless there is an analogy to made to some logic. Is there a combinatorial analogy for the hypercube just as the simplex has "m choose n"? https://en.wikipedia.org/wiki/Binomial_coefficient

I see that in your paper you use some arrow symbols next to hypercubes and cross-polytopes, but I don't know what you're saying with those symbols. My apologies. Intuitively, there *should be* some interesting combinatorial logic in the hypercube triangle since it is an expansion of the coefficients (x+2)^n whereas Pascal's triangle is (x+1)^n.

> > What guides my thinking here is an attempt to combinatorially interpret > the Pascal's triangle that accords with an infinite family of polytopes, > or more broadly, "choice frameworks". In the case of the simplexes, I > note that we need to make sense of the -1 simplex which always has a > value 1. It seems natural to identify this with the unique center of the > simplex. That may seem natural, but why isn't it natural for the cube?

> > In the case of the cross-polytopes, and specifically, the octohedron, it > is curious that the row 1,6,12,8 ends with the 8 faces. There is no "1" > at the end for the volume. Which is to say, combinatorially, the > octohedron isn't defined to have a volume.

Does anyone else corroborate this idea?

> Combinatorially, based on > the numbers, we should think of an octohedron as culminating in a > surface with eight faces. Thus we have a family with a single, unified > center but with no single, unified totality. The dual of the > cross-polytopes are the hypercubes and thus we get the opposite, a > totality but no center. Instead of a center we have 8 corners, vertices. > > The coordinate systems have neither center nor totality and aren't even > polytopes. But they fit within this scheme as one of four choice frameworks.

Unless I am mistaken, you said the corners of an 8 part cube (1, 3, 3, 1) are a coordinate system which would seem to suggest the next cube totaling 27 points is also a coordinate system. Forgive me if this is wrong. A 27 part cube would have a center among its coordinates and slices (1, 3, 6, 7, 6, 3, 1) The 7 in the center represents a hexagon with central dot, meaning this coordinate system has a center. What is your scheme?

> > The point is not to consider the shapes in terms of what we look like to > us, but rather to consider what we are told about the shapes by the > triangles of numbers which define them. Moreover, to think of the > shapes in terms of the rules that generate those triangles of numbers. > That is what the math is trying to tell us. Can we listen to the math?

I agree that the shapes are fundamentally ideas and not just outside appearances, so I will attempt to imagine a scheme where your way of counting makes sense. It is tempting to imagine hypercubes and cross-polytopes as multiplying points or dividing space. I have already associated both with 1, 3, 9, 27... so let's divide a string or multiply its length to make a tuning system.

1/27 1/9 1/3 1/1 3/1 9/1 27/1

To make these ratios intervals in a scale, it is traditional to put them within the span of an octave. so 1/27 must be multiplied by 2 until it is between 1 and 2, and 27/1 must be divided by 2 until it is between 1 and 2:

1/1 9/8 32/27 4/3 3/2 27/16 16/9 2/1

https://en.wikipedia.org/wiki/Pythagorean_tuning

However, there is a different way of thinking of and generating these intervals. It is called the "spiral of fifths". The spiral of fifths is an infinite series of intervals, similar in name to the modern "circle of fifths", but the modern circle is a creation of equal temperament which allows a certain number of fifths to equal a certain number of octaves exactly. These successive perfect fifths (3:2) are plotted on a spiral because they can never return to an octave (2:1).

To make the spiral simply raise and lower 3/2 to successive powers:

 (3/2)^-3 (3/2)^-2 (3/2)^-1 (3/2)^0 (3/2)^1 (3/2)^2 (3/2)^3 =

 8/27 4/9 2/3 1/1 3/2 9/4 27/8

Then these intervals must be multiplied or divided by 2 until they are within the span of a single octave to make a scale, but then, what's the point? Why not just do 3/1 9/1 27/1 first? They will be divided by 2 until within an octave regardless, right? The spiral reveals extra information because every position in the spiral matches the position the intervals will take within a single octave. For example:

1/1 3/2 2/1 9/4

2/1 ÷ 9/4 = 1/1 ÷ 9/8

9/4 would become 9/8 when normalized to a single octave, but 9/4 is already the same distance from 2/1 as 9/8 is from 1/1. The same applies to

2/1 ÷ 27/8 = 1/1 ÷ 27/16,

4/1 ÷ 81/16 = 1/1 ÷ 81/64,

etc...

Musically, this isn't unusual or unnatural if put in the framework of the harmonic series: https://en.wikipedia.org/wiki/Harmonic_series_(music)

1, 2, 3, 4...

That 3 comes after 2 and that they are in 3:2 proportion needs no explanation, but this isn't meant to be a profound truth or proof of anything. It's just a perspective where 3 doesn't stand alone but in context (after 2). What is interesting are the spiral intervals that result from 3:2 instead of 3:1 : 1/1 3/2 9/4 27/8

If these were hypercubes, they conveniently display their numbers of vertices (or facets in the case of cross-polytopes) along with their total number of parts. Even better is that there is simultaneously a reciprocal series which is suggestive of a geometric duality metaphor. If 2, 4, 8, 16, etc are simplices, then each interval shows what kind of simplex the shape is made of 27:8 corresponds with cross-polytope made of 8 triangles, or alternatively 8 is the description of the hypercube's vertex connections (1 point, 3 edges, 3 squares, 1 cube interior).

Actually, this line of thinking invokes Plato's triangle mentioned earlier:

    1
   2  3
  4  6  9
 8 12 18 27

1, 3, 9, 27 has an obvious connection to hypercubes, so is there a way to interpret the other numbers? 3 = (2 vertices, 1 edge). There is no such thing as a more primitive line segment than this. A compound segment with (3 vertices, 2 edges) = 5 can be made, but that doesn't help. 2 cannot be a finite line segment, because to remove one endpoint makes a segment infinite or indefinite on one end. If 1, 2, 4, 8, etc... are expanded to rows of Pascal's triangle, 2 = (1, 1). 1 vertex, 1 edge? What could this be? Actually, every row of Pascal's triangle *could* indicate an object with 1 vertex for every dimension.

My convenient explanation for this is that a vertex is a singular thing in 0 dimensions, but in 1 dimension and higher, Pascal's triangle can be interpreted as listing the number of things a hypercube vertex connects to, so (1, 1) is a 1 dimensional vertex existing in the context of a segment, (1, 2, 1) a 2 dimensional vertex on a square, etc... (because the corner of a square touches 1 (itself), 2 edges, 1 square)

The different series 1, 2, 4, 8; 3, 6, 12, 24; 9, 18, 36, 72; and 27, 54, 108, 216 can all correspond to a different pascal-type table. All that is required is to start with the f-vector of a hypercube such as (2, 1) or (4, 4, 1) and proceed like so:

   2 1   = line segment         4 4  1    = square
  2 3 1  = edge on a square    4 8  5 1   = connections of square on a cube
 2 5 4 1 = edge on a cube     4 12 13 6 1 = square on a tesseract

This gives Plato's triangle the following interpretations:

             0D point
        1D point 1D segment
    2D point 2D segment 2D square
 3D point 3D segment 3D square 3D cube

                   1 point
          1 vertex         2 vertices (segment)
       1 edge      2 edges      4 edges (square)
 1 triangle 2 triangles 4 triangles 8 triangles (octahedron)

It's just repeating point, line, plane, solid in different ways, but the impressive thing is connecting the doubling of geometric parts to the musical idea of "octave equivalence". https://en.wikipedia.org/wiki/Octave#Equivalence

The idea is that sounds in 2:1 ratio sound so similar that they are musically equivalent in many ways except one is higher and the other lower but otherwise act the same way and play the same role, which seems pretty similar to the geometric ideas above.

This connects your version of the simplex to the octaves of hypercube vertices or cross-polytope facets giving (1, 3, 3, 1) a more specific meaning, a triangle in the context of an octahedron or a triangle existing in 3D space. (1, 3, 3, 1) vs (3, 3, 1). 8 vs 7. 7 isn't living in harmony with the octahedron. It stands alone in 2D, incommensurable with squares, implying discord. 8 is an "octave simplex" living in harmony with the octahedron in 3D.

Curiously attributed to Plato are these ideas: https://en.wikipedia.org/wiki/Plato%27s_unwritten_doctrines#The_two_fundamental_principles_and_their_interaction

"The One: the principle of unity that makes things definite and determinate

The Indefinite Dyad: the principle of 'indeterminacy' and 'unlimitedness'"

Suppose that we have a 1 part point (.) and a 2 part indeterminate line segment or ray (<-.)

The ray---playing the role of (x + 1)---may combine with the point to produce a 3 part segment .-. which is definite, and the ray may combine again with the segment to produce .-.-., etc, which is an unlimited principle of succession. (0+1+1+1...)

 "The Tao produced One; One produced Two;
 Two produced Three;
 Three produced All things."

---Tao Te Ching, Chapter 42

---

September 2, 2002

Hello Mr. Kulikauskas,

You describe yourself as an independent philosopher, so I do not imagine geometry being the highest priority for you but nonetheless I want to understand your perspective.

I read your page on some infinite polytope families here: http://www.ms.lt/sodas/Book/DiscoveryInMathematics

What is your reasoning for counting the center or totality of one family but not the other? Most importantly, why does the simplex alone have both center and totality? Obviously any polytope such as a cube can be navigated such that a center is found or created, and a sphere large enough can be made such that it is surrounded to suggest a totality, but I assume you refer to a more subtle idea. I apologize if I missed the nuance of your explanation. Can you elaborate for me?

An alternative interpretation of Pascal's triangle is that each row lists the slices of a hypercube in figurate numbers.

1+4+6+4+1 = 16

Point, tetrahedron, octahedron, tetrahedron, point.

These are slices of a tesseract. A tesseract has 16 vertices.

This interpretation puts Pascal's triangle in a family of triangles, the next one with rows sums totaling 3^n, the trinomial triangle, which starts:

 1
 1 1 1
 1 2 3 2 1

These triangles all show the slices of higher and higher order hypercubic figurate numbers. If desired, the trinomial triangle can be arranged as a square, the next triangle as a pentagon, and the next as a hexagon, etc for aesthetic purposes.

Yours would be a nice paradigm if I understood it, because it might lead to an elementary mapping of geometry to music. Having simplices represent octaves and hypercubes/cross-polytopes represent powers of 3 would be enough to create a Pythagorean music scale. The perfect fourth and perfect fifth are inversions of each other. The octave is "self-inverting" or self-dual. Tonic note, fourth, fifth, and octave are the sole generators of a 3-limit scale.

Thanks for your time.