• View
• Edit
• History
• Print

I am trying to understand Schur-Weyl duality.

Why master this?

Schur-Weyl duality is an overarching duality that unifies six other dualities.

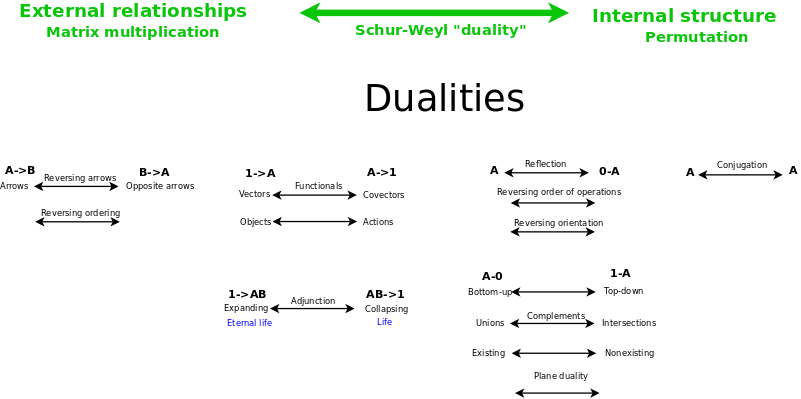
Schur Weyl duality relates the general linear group and the permutation group, thus relates:

• the duality of external relationships, where {$A\rightarrow B$} is dual to {$B\rightarrow A$}, as in matrix multiplication, where {$a_{ij}$} is dual to {$a_{ji}$}
• the duality of internal structure, where conjugates {$i$} and {$j$} are indistinguishable and of equal significance, as with permutations.

How to learn this?

Some related concepts to learn are:

• Category of representations. In this category, the morphisms are the equivariant maps.
• Frobenius reciprocity This is an adjunction between the functor {$\textrm{Res}^G_H$} restricting a linear representation of a group {$G$} to a linear representation of its subgroup {$H$} and the functor {$\textrm{Ind}^G_H$} inducing a linear representation of {$G$} from a linear representation of {$H$}. This adjunction {$\textrm{Ind}^G_H \dashv\textrm{Res}^G_H$} is of additional interest because if {$G$} and {$H$} are finite groups, then also {$\textrm{Res}^G_H \dashv\textrm{Ind}^G_H$}. I want to understand this adjunction from both sides.
• Maschke's theorem states that every representation of a finite group G over a field F with characteristic not dividing the order of G is a direct sum of irreducible representations. It seems this theorem makes use of the concepts of restriction and induction. I am also interested in the module theoretic version of this theorem because it is related to Wedderburn-Artin theorem which describes how semisimple rings are products of finite-dimensional matrix rings over division rings. The latter theorem is used in the classification of Clifford algebras and thus is relevant for Bott periodicity.

I am watching a helpful series of videos by Monica Vazirani: Representation Theory and Combinatorics of the Symmetry Group and Related Structures, Part II, Part III.