• View
• Edit
• History
• Print

Research program, Research program introduction

This is an old draft.

The ABC's of Thinking in Parallel

First Glimpse: Introductory structures

Introduction

Goals for this video

• Introduction to Math4Wisdom

Personal goals

• Find support and income to get by.

Questions of interest

Understand intuitively

• In algebraic topology: Bott periodicity, Clifford algebras.
• In category theory: Adjoint functors, the Yoneda lemma.
• In Lie theory: the four classical families of Lie groups and Lie algebras, and how they relate to affine, projective, conformal, symplectic geometries.
• In particular: master SU(2), SU(3), including their gauge theories.
• The Poincare group.

These are mathematical structures which I am working to interpret as frameworks for how cognitive perspectives fit together.

Thinking-in-parallel

Thinking in parallel - the three basic ways

• Thinking-in-parallel is a key property of experiencing life and being aware of the thinking-in-parallel which proceeds inside of you is key for your own wisdom.
• We can grow aware of thinking-in-parallel by respectfully listening to another's perspective while maintaining one's own independent perspective.
• We grow further aware by having internal dialogue.
• We grow more aware by studying the nature of that dialogue, how perspectives fit together as cognitive frameworks to flesh out existential issues.
• Two-track mind for existence, three-track mind for participation, notably for learning, and a four-track mind for knowledge.
• The basics for wisdom - look for them in mathematics.

More questions of interest

I will keep switching back and forth between mathematics and wisdom so as to maintain interest among those of you who are primarily interested in advanced mathematics and those who may not understand any of it but are very keen to investigate wisdom.

Here are some more subjects in math that are relevant for how perspectives can fit together.

• Understanding the Schroedinger equation and quantum field theory in terms of the combinatorics of orthogonal polynomials.
• The Chomsky hierarchy in automata theory.
• The arithmetic hierarchy in computability theory.
• Universality principle, random matrices, in statistics and dynamical systems,
• Univalence axiom in homotopy type theory.
• Entropy.
• Sequences, hierarchies, networks.
• Random walks on binary trees.

Goals that relate math and wisdom

• Show mathematicians structures to be on the look out for.
• Show my philosophy as a work-in-progress that is coming together.

Initial examples

Definitions

• In terms of ever more fundamental concepts
• Axioms are conditional. What is unconditional?
• Holistic way of looking - consider math holistically

Example: One-all-many

• One-all-many based on constancy

Other representations

• Necessary, actual, possible - logic - truth is "obvious", trivial (as mathematicians say)
• Object, process (morphism), subject - category theory (missing subject)
• One, many, all
• Being, doing, thinking - group theory (action)

In fact, all of the arrows in this diagram correspond to some hidden context involving people: the prediction is dependent on who analyzes the hypothesis, the specification of an experiment is dependent on who is motivated to specify it, and experiments may result in different observations by different observers. ... By choosing a monad we can make explicit (and then hide from discourse) our implicit assumption that “of course this is all dependent on which human is doing the science”. (David Spivak, Category Theory for Scientists (old version), pg.242.)

12 categories

• Kant's categories - why they differ
• Kant's categories - logical form (A -> B) - much like category theory
• Mind games
• Vocabulary of the imagination
• Example of conceptions - representations

Deeper example: Three-cycle

• Even deeper: three-cycle because based on self-relationship.
  • Where is the constancy? In taking a stand (one), following through (all), reflecting (many).

How I came upon it at the University of Chicago. What is happiness?

Philosophy

• Scientific method
• Sesame street
• Army action review

Roger Penrose His book "The Road to Reality" is a thousand page survey the mathematics used in physics. He has made it available online for free. He begins with a self-analysis of his prejudices that he encapsulates in this picture.

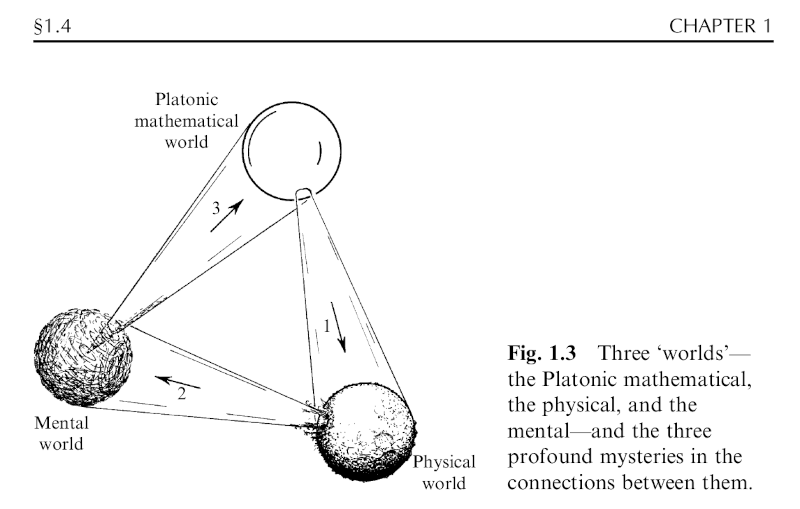
mathematical laws, actions of the universe, the scope of reason

• "everything in the physical universe is indeed governed in completely precise detail by mathematical principles"
• "all of mentality has its roots in physicality"
• "there are no mathematical truths that are beyond the scope of reason"

He concludes, "How can it be that, in accordance with my own prejudices, each world appears to encompass the next one in its entirety? I do not regard this issue as a reason for abandoning my prejudices, but merely for demonstrating the presence of an even deeper mystery that transcends those which I have been pointing to above."

What more could he do with these ideas? Who could he talk with about them? The goal of Math 4 Wisdom is to present and develop ways to meaningful approach such ideas.

He tried to connect them with Plato's values of truth, beauty and good. There was not clear connection. However, we can assert one with the scientific method.

The hypothesis is formulated in the mathematical world, the experiment takes place in the physical world, the observation is perceived in the mental world.

Scientific method basis for agreement

• Prophet Daniel - eating vegetables
• Jesus: judge the tree by the fruit - otherwise sin against the Holy Spirit
• McMaster Institute leader change of mind
• judge my ideas by their fruits - that is why I'm focusing on math
• mathematicians and physicists have blindspots

Note that others consider the scientific method to have more steps.

• Repeats twice: "analyzed by a person yields", "analyzed by a person produces"
• Three are actually relevant: "When, in an experiment, the observation matches the hypothesis—success!—that is agreement." Spivak, Category Theory for Scientists (free version) pg.7 Note that here he conveys the entire sense with only three terms: hypothesis, experiment, observation. And we see that hypothesis is stating before the experiment and observation is stating after the experiment. Experiment is as if the tensor product of the other two.

David Spivak. Categorical interaction in the polynomial ecosystem.

Khan Academy. The Science of Biology The scientific method has five basic steps, plus one feedback step:

• Make an observation.
• Ask a question.
• Form a hypothesis, or testable explanation.
• Make a prediction based on the hypothesis.
• Test the prediction.
• Iterate: use the results to make new hypotheses or predictions.

Wikipedia: Scientific Method describes a four step or six step process.

• diagram

Double loop learning

• Working to uncover a language of truth for deep agreement.
• Uncover the deep structures and then explain the variants that arise.
• Math can help provide a status of a deeper truth

Give math examples:

• SU(2) - Pauli matrices, quaternions
• Triangulation - learning about a surface - not reversible
• Cross product - learning the surface ?
• Jacobi identity - Lie algebra is learning the Lie group
• ABC=CAB linear Turing machine - tangential
• Curry-Howard-Lambek programming languages, type theory, category theory (directionality unclear)(and also considered as a tetralogy)(but note eight levels of logic)
• Long exact sequence - derived functors, learnability - injective resolutions (exhibits directionality)
  • explain relation to the existence of holes, what is not
• Fiber sequences, Fiber bundle, Mapping cone (cofiber)
• F → E → B (take a stand -> follow through -> reflect) examples: cylinder (exact), Moebius strip (not exact for line segment - get leftover space - so use double line segment).
• {$\cdots\to\pi_n(F)\to\pi_n(E)\to\pi_n(B)\to\pi_{n-1}(F)\to\cdots \to \pi_{0}(F) \to \pi_{0}(E)$}
• "the long exact sequence of homotopy groups follows from the fact that the homotopy groups can be obtained as suspensions, or dually, loop spaces."
• Puppe sequence
• Triangulated category and, in particular, Derived category But some experts suspect that triangulated categories are not really the "correct" concept.
  • Wisdom is a guide for deep mathematical insights. Pythagoras, Descartes, Pascal, Leibniz, Frege, Whitehead. And if a philosopher's insights aren't providing mathematical insight, then in what sense is their thinking sound, solid, applicable, verifiable, fruitful? Or perhaps they are providing metaphysical insight, then let us show where and how that expresses itself in mathematics. Metaphysics is conceptual mechanics - where by concepts not meaning so much the formal sense but moreso the issues they refer to.
• four ways of looking at a triangle - four geometries
• Goedel's theorem - and a three-cycle as a state which can be contradictory yet inhabitable

Goals for Math4Wisdom

Goals for Math 4 Wisdom

• Express my concepts in terms of math.
• Show that my concepts are relevant and fruitful in math.
• Present a language for
• Foster a community.
• Overview all of math - the areas, concepts, questions, results...
• Identify and appreciate the key concepts behind mathematics.
• Understand and apply the nature of mathematical beauty.
• Address the shortage of materials for appreciating, contemplating, exploring advanced mathematical topics and especially, gaining a sense of the big picture.
  • A sort of guide for mountain climbers (or cave explorers or mental prison explorers).
• Show the usefulness of wisdom as a guide in making sense of mathematics and the relevance of various mathematical topics to expressing wisdom.
  • A bit like an alternative reality for wizards except its real - Jesus, Buddha, Mohammed, Harry Potter.
• Show the reality of cognitive frameworks.
• Way to engage those who might work together.

General idea of my philosophy

• Relate the definite and the indefinite.
• Math is most definite. So show how the indefinite relates.
• For example, how axiomatic mathematics is inspired by nonaxiomatic premathematics.

General approach

• Ways of figuring things out in math.

Twosome

• Twosome
  • For existence rather than participation
  • Examples:
• Tensor product (opposites coexist, in parallel, geometry (homogeneous choice)) vs. Homset functor (all is the same, in series, algebra (step-by-step)).
• Outside-inside (orientable - nonorientable)
• Limits (softwiring external relationships) colimits (hardwiring internal structure). Softwiring precedes hardwiring.

"Interestingly, a graphic has the power to evoke feelings of understanding, without really meaning much. The same is true for text: it is possible to use a language such as English to express ideas that are never made rigorous or clear. When someone says “I believe in free will,” what does she believe in? We may all have some concept of what she’s saying—something we can conceptually work with and discuss or argue about. But to what extent are we all discussing the same thing, the thing she intended to convey?" Spivak, Category Theory for Scientists (free version) pg.7

Nonexamples

• Discuss yin-yang.
• Seven kinds of duality - sevensome. Will relate to Bott periodicity.
• Male-female gender.

What is wisdom - knowing everything

Wisdom - knowing everything - knowing something or anything about everything - what can we say about how everything is organized?

• Mental chambers - arguing various issues
• Guide through a mental prison - understanding the limits of the imagination - venture into the mathematical caves.
• Relate the language of wisdom and the language of math.
• I speak the language of wisdom.
• Intuition - extra dimension - depth perception instead of time.
• My approach is to observe the limits of my imagination, to document the cognitive frameworks by which I and others live and think, to

Foursome

• Another example: foursome
  • Levels of knowledge.
  • Example: the bottle
  • Plato, Aristotle
  • Idealism vs. materialism
• Peirce's signs
  • progression in evolution
  • natural transformations distinguish - icon, index
  • thing - identity morphism = object (object is what has an identity morphism - whether it is an object)
  • symbols - absolutely any relationship
• Yoneda Lemma, embedding
  • functions like knowledge switch

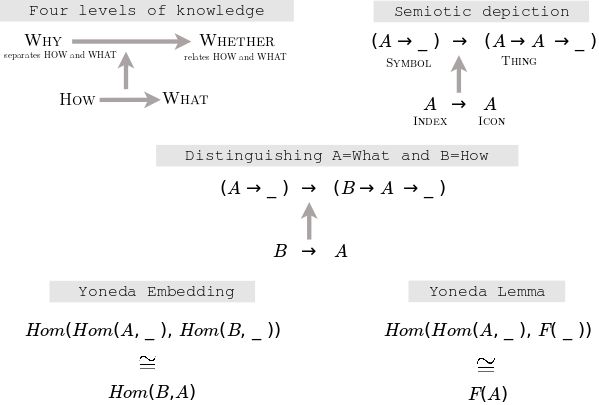
Consider also the case where F is the identity I, and thus A is a set. Look at the natural isomorphism.

• global quantum - Maxwell's demon operates the knowledge switch - Bible story - how physicists talk about the global quantum - that you run out of tape - Rolf Landauer - but they don't specify the cut off
• automata theory Chomsky hierarchy.

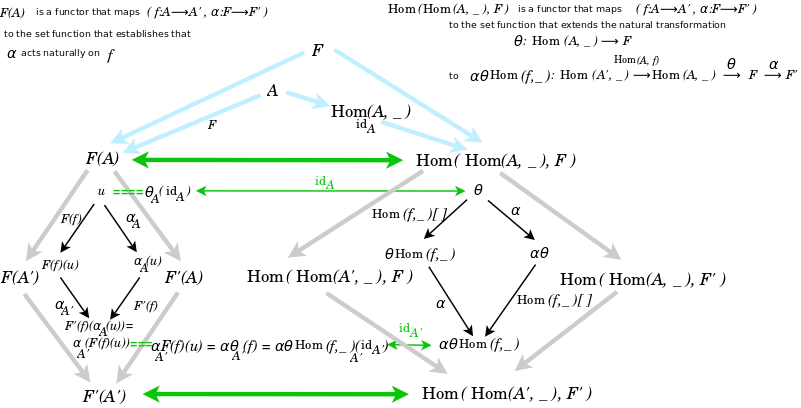
In his comment at Math Stack Exchange, Nex describes the two functors {$ R $} and {$ L $} thusly:

• {$ R $} is {$ ((α,f):(F,A)→(F′,A′))↦(x↦α_{A′}(F(f)(x))) $} and the objects are mapped {$ (F,A)↦F(A) $}
• {$ L $} is {$ ((α,f):(F,A)→(F′,A′))↦(θ↦(α⋅θ⋅\textrm{Hom}(f,−))) $} and the objects are mapped {$ (F,A)↦\textrm{Nat}(\textrm{Hom}(A,−),F) $}
  • • Consider the distribution of the largest eigenvalue for a random matrix. The peak is at {$\sqrt{2N}$}. The distribution drops as {$e^{-N^2}$} to the left and as {$e^{-N}$} on the right.
    • Finite automata - strong coupling - scale as N^2. Push-down automata - subsystems - weak coupling - scale as N.
    • How could the largest eigenvalue be larger than expected? There are not many ways and thus it drops down quickly. How could it be smaller than expected? There are many more ways, mixing positive and negative, and thus it drops down slowly.
    • Quanta Magazine. Beyond the Bell Curve - A New Universal Law Satya Majumdar, Grégory Schehr. The critical point at √2N separates a stable phase of weakly coupled species, whose populations can fluctuate individually without affecting the rest, from an unstable phase of strongly coupled species, in which fluctuations cascade through the ecosystem and throw it off balance. In general, Majumdar and Schehr believe, systems in the Tracy-Widom universality class exhibit one phase in which all components act in concert and another phase in which the components act alone. The asymmetry of the statistical curve reflects the nature of the two phases. Because of mutual interactions between the components, the energy of the system in the strong-coupling phase on the left is proportional to N2. Meanwhile, in the weak-coupling phase on the right, the energy depends only on the number of individual components, N
    • Universality principle " as the phase transition is approached, the scale-dependent parameters play less and less of an important role, and the scale-invariant parts of the physical description dominate. Thus, a simplified, and often exactly solvable, model can be used to approximate the behaviour of these systems near the critical point. "
  • Two objects cannot be in the same place, and the same is true for fermions. But two arrows can be in the same place, and the same is true for bosons. I mean to say that two arrows can start at the same object and end at the same object but be entirely different arrows. So a shift from an "object point of view" to an "arrow point of view" may be like a shift from "fermion statistics" to "boson statistics".
  • Univalence Axiom {$(A=B)\simeq(A\simeq B)$}
  • Yates index theorem, the jump hierarchy.
    • Unconscious, conscious, consciousness
  • 4 sheave functors
  • Feynman diagrams with 4 fields

Everything

Four properties of everything

• Russell's paradox

Divisions of everything

• Onesome

Division of everything into zero perspectives

• 4 representations generate nullsome
• Foursome negates them
• All fits together

Cube? fits tightly together

Theory regarding the Facts

• Search for Definition ultimately leads to the Indefinite
• The Indefinite, Definite, Imaginable, Unimaginable
• Something like God
  • Recommend Carroll's video "Why God is not a good theory"
  • Omniscient vantage point - important for gaining intuition about knowing everything - including how I relate to God and how others relate to God
  • the spirit of everything - everything is the structure of God
  • The zeroth person.
  • The vantage point of the one who loves us more than we love ourselves.
• The state of contradiction - God
• Proof by contradiction - how can anything come from God
• God goes beyond himself into himself
• Goedel's theorems
• General question - how can a consistent system arise from inconsistency - that is where Bott's periodicity comes in
• Another model: F1 - zero, one, infinity
• Fixed points
• SU(2) relates zero, one, infinity

Relevance of God - source for mathematical intuition

• Peacemaking - "love your enemy" (unconditionality allows for negative numbers)
• Check oneself (myself) when one challenges another to grow, am I doing it for selfish reasons?
• Be able to live closer to the edge, thus learn more about life, not in an ivory tower - economically, socially.

Not math for its own sake

• but stay open minded
• Baez 5, 8, 24 - favorite numbers - will talk about them
• Projective geometry for octonions, magic square
• Albert R+C+H
• R+C+H+O and octonions
• E8
• cellular automata

Short Summary of wisdom

• Eternal life
• Overview of theological purpose - God does not have to be good
• Longer summary at the end of the series

Goals for wisdom

Goals for wisdom

• Main ways the indefinite is important.
• Solve technical issues.
• Relate different houses of knowledge.

Goals for language

• Create a language for working together as a scientific community.
• I look to math as a standard of truth for such expression, for such a language.

Goals for community

• Support inclusive harmony of self-realization of all people - "meaningful inclusion".
• Shared question, "How to love each other more"
• Sharing life experiences, deepest values, investigatory questions, etc.
• My personal goal is to express myself fully as I wish for others as well.
• So I am expressing myself through arts and with examples from all of life.

End of Introduction

• ABC's - twosome, threesome, foursome
• See how they come up in more comprehensive and elaborate structures
• Consider a more sophisticated structure, the fivesome.

This is my introductory video to explain what Math for Wisdom means to me, and in particular, the research program I intend to pursue, which you may help with, learn from, and support through Patreon.

My name is Andrius Kulikauskas. I am speaking from my home in Lithuania. Please visit my website, Math4Wisdom.com, where you can read the text for this video, observe my research activities, contact me and perhaps collaborate with me or others.

I am learning, studying, exploring and discovering advanced mathematics at a graduate student level which is relevant for my quest since childhood to know everything and apply that knowledge usefully. I have in mind a very particular set of mathematical structures which I believe express cognitive frameworks for wisdom that also serve as keys for making sense of all of abstract math. I need to learn enough category theory to classify adjoint strings and master the Yoneda lemma, enough algebraic topology to intuitively understand Bott periodicity inside out, enough algebraic geometry to be able to explain why there are four infinite families of Lie groups and algebras and how they lay the foundations for four geometries - affine, projective, conformal and symplectic geometries.

math includes ...

By knowing everything, I mean a Godly, perfect, total, complete, absolute knowledge of the vantage point from which everything makes sense, from which we have the big picture. Of course, from the heights of that Olympus my human-sized brain and my nearsighted eyes will not penetrate through all the clouds below, will not engage all the details at once. Therefore by knowing everything, I also mean the further ability to descend into the details, to readily find the answer to any particular question we may have, including any mathematical question, and then to climb back up to that perfect vantage point. Certainly, I would want to be able to explain where all of math comes from, and how it unfolds, all of the branches, concepts, structures, theorems, questions, ideas, challenges, opportunities, in all their possible directions and subdirections. And if I did do that, if I laid out all of mathematics before you, so that you could see with childlike fascination, at every step, the options by which it proceeds, up through the most impossibly profound results, all of the mathematics that there could every possibly be, as if you were exploring a miraculous fractal world, zooming through a Mandelbrot set of ideas, then I would feel comfortable, I would feel emboldened to tell you that my findings about the wisdom of life may likewise be valid. The goal of knowing everything, the proper, useful, beautiful application of that knowledge, is for independent thinkers to foster a community, nurture a science, develop a conceptual language, not just for a map of mathematics but for all of human life, especially that wisdom by which we grow ever more mature, here and now. Math for wisdom is a call around the world to those who are working towards this goal from every imagineable world view. If we want to be sure of exactly what we mean, and be confident that we have uncovered a conceptual language of well formed, well connected and well functioning ideas, and hope that others will trouble themselves to understand, then we should express ourselves in terms of mathematics, or rather, in terms of mathematical ideas, those ideas that mathematics researchers know from their work. Math is the gold standard for utility of expression, which true philosophy should meet, and which sincere poetry admiringly concedes.

Math for Wisdom is my way of engaging you with the topics in advanced mathematics that are relevant for expressing to others the conceptual language that I seek for my own thinking but ultimately for thinking along with you.

In this very first video, I am providing an overview for myself to make clear why and how I personally take up and pull together a variety of mathematical investigations. For my sake and for your sake I believe that I should start with such a straightforward approach. In the future, depending on what you find interesting, I expect to present my investigations in ways that ...

The universal conceptual language that I seek is, like math, an alternative to words. We may use a word like "tree" pragmatically, simply because we want to refer to the chair next to the tree, and so we need not agree as to what we actually mean by tree. If we were to take a tree and make it smaller, then at some point we would surely disagree as to whether it is still a tree or has become a bush. We simply don't need to know or care to know exactly what we mean by tree.